Kezdőlap


Cím:	Önhasonlóság az Interneten
Szerző(k):	Fekete Attila
Füzet:	2001/április, 236 - 243. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

2000. júniusában az ERICSSON cég kutatási szervezete és az ELTE TTK együttműködési szerződést írt alá; közös kutatási program megvalósítására létrehozták a Kommunikációs Hálózatok Laboratóriumát. A programban a ,,komplex rendszerek'' kutatásával foglalkozó oktatók, PhD ösztöndíjasok és egyetemi hallgatók vesznek részt. Az alábbi cikk ‐ amely a tavalyi Téli Ifjúsági Ankéton tartott előadás kibővített változata ‐ ennek a kutatásnak egy érdekes ágáról számol be.

1. Bevezetés

Az Internet születését 1969-re, az amerikai ARPANET (Advanced Research Projects Agency NET) megalakítására szokták datálni. Az ARPANET egy számítógépes hálózatot jelentett, amelyet azért hoztak létre, hogy az ARPA programban résztvevő, egyre népesebb kutatócsapat meg tudjon osztozni a rendelkezésre álló, ám korlátozott számú számítógépen. Pár éven belül aztán a hálózatot megnyitották az egyetemek és a nagyközönség számára is, amivel megkezdődött a mai Internet rohamos terjeszkedése.

1. ábra. Egy vezetékes telefonhálózat sematikus váza. A készülékek a telefonközponthoz kapcsolódnak, amelyek egymás között irányítják a hívásokat a hívott félhez Az Internet első pillantásra teljesen megegyezik egy klasszikus telefonhálózattal (1. ábra), csupán a telefonkészülékeket kell képzeletben számítógépekre cserélni. Egészen 1989-ig valóban ez az elképzelés uralkodott a mérnökök és kutatók között, ekkor azonban olyan mérési eredmények láttak napvilágot, amelyek azt mutatták, hogy a két rendszer működése között alapvető különbség van.
A következőkben röviden bemutatunk egy telefonhálózatok leírására alkalmas modellt. Ezután vázlatosan ismertetjük az Internet adatforgalmát szabályozó egyik lefontosabb algoritmust, a TCP-t. Megadunk néhány mennyiséget, amelyek az adatforgalom statisztikus tulajdonságait jellemzik, és megmutatjuk, hogy miben térnek el ezek a tulajdonságok az Internetnél és a klasszikus telefonhálózatoknál. Végül ismertetünk egy elképzelést arról, hogy milyen mélyebb oka lehet az Internet klasszikustól eltérő viselkedésének.

2. A telefonhálózat egy modellje

Képzeljünk el egy telefonközpontot, ahova a település

N

lakójától egymástól függetlenül és véletlenszerűen futnak be a hívások. Tegyük fel, hogy a telefonközpont

m

hívást tud fogadni egyszerre, és ha minden vonal foglalt, akkor a telefonálónak várakoznia kell. Feltesszük, hogy a várakozók egy sorban állnak, ugyanúgy, mint például a nézők a mozipénztáraknál¹.
Osszuk fel az időt nagyon rövid

Δ t

intervallumokra. Tegyük fel, hogy a

Δ t

időintervallum alatt

p

valószínűséggel kezdeményez valaki új hívást, függetlenül attól, hogy mikor telefonált utoljára, és

q

valószínűséggel teszi le valaki a kagylót, függetlenül attól, hogy mióta telefonált. A telefontársaság részéről egy lehetséges kérdés az, hogy hány hívás fogadására alkalmas központot telepítsen az adott városba. Kézenfekvő válasz lenne, hogy

N

-et, ez azonban igen gazdaságtalan volna, mivel nagyon kicsi annak a valószínűsége, hogy egyszerre mind az

N

lakó telefonálni akar. Pontosítva tehát a kérdést: hány hívás fogadására legyen alkalmas a központ, ha azt akarjuk, hogy

ε

valószínűsége legyen csak², hogy valakinek várakoznia kell, mert nem kap vonalat egy adott

Δ t

időintervallumban.
Egy nagyon hasonló problémát már 1917-ben megoldott A. K. Erlang (1878‐1929) dán matematikus. A megoldást Erlang-formulának nevezik a távközlésben. (A mozipénztáraknál nem nevezik Erlang-formulának a megoldást, pedig ugyanez érvényes ott is.)
A feladatot a következőképpen lehet megoldani. Jellemezzük a rendszert azzal az

n

természetes számmal, amely megadja, hogy hányan akarnak éppen telefonálni egy adott

Δ t

időintervallumban. Ha

n

lakó akar telefonálni, akkor azt mondjuk, hogy a rendszer az

n

-edik állapotban van. Feltettük, hogy

Δ t

igen kicsi, ezért csak a következő három eseménynek van számottevő valószínűsége (2. ábra):

*	1.Újabb telefonáló érkezik, azaz átlépünk az $(n + 1)$ -es állapotba. Ennek a valószínűsége $λ_{n} Δ t \equiv p (N - n) Δ t$ , mivel $(N - n)$ lakó veheti fel a telefont.

*	2.Valaki leteszi a kagylót, vagyis átlépünk az $(n - 1)$ -es állapotba. Ennel a valószínűsége $μ_{n} Δ t \equiv q n Δ t$ , mivel $n$ ember telefonált éppen.

*	3.Nem történik semmi, maradunk az $n$ -edik állapotban. Ennek a valószínűsége $1 - (λ_{n} + μ_{n}) Δ t \equiv 1 - (p (N - n) + q n) Δ t$ , mivel valamelyik eset biztosan bekövetkezik, ám egyszerre mindig csak az egyik.

2. ábra. Az

n

-edik állapothoz tartozó átmeneti valószínűségek (folytonos vonal).
Jelöljük

P_{n}^{*}

-nel annak a valószínűségét, hogy a rendszer hosszú idő elteltével az

n

-edik állapotban tartózkodik. Megmutatható, hogy ez a rendszer olyan, hogy a kezdőfeltételtől³ függetlenül

P_{n}^{*}

hosszú idő múlva egy meghatározott értéket vesz fel. Az is belátható, hogy teljesül a következő egyenlet:

\begin{matrix} λ_{n - 1} P_{n - 1}^{*} = μ_{n} P_{n}^{*}, \end{matrix}

(1)

amelyet a részletes egyensúly elvének is neveznek, és szemléletesen azt fejezi ki, hogy átlagosan ugyanannyiszor lép a rendszer az

(n - 1)

-edik állapotból az

n

-edikbe, mint az

n

-edikből az

(n - 1)

-edikbe. Az (1) egyenlet egymás utáni alkalmazásával könnyen kapjuk, hogy

\begin{matrix} P_{n}^{*} = \frac{λ_{n - 1} λ_{n - 2} ... λ_{0}}{μ_{n} μ_{n - 1} ... μ_{1}} P_{0}^{*} . \end{matrix}

(2)

Mivel a rendszer biztosan valamelyik állapotban tartózkodik, ezért

\begin{matrix} \sum_{k = 0}^{N} P_{k}^{*} = 1. \end{matrix}

(3)

Az előző két egyenletből, valamint

λ_{n}

és

μ_{n}

definíciójából végül az kapjuk, hogy

\begin{matrix} P_{n}^{*} = (\binom{N}{n}) {(1 + \frac{p}{q})}^{- N} {(\frac{p}{q})}^{n} . \end{matrix}

(4)

Ennek segítségével már válaszolhatunk a felvetett problémára. Tegyük fel, hogy

m

telefonálót tud kiszolgálni a központ. Annak a valószínűsége, hogy valaki nem tud telefonálni:

\begin{matrix} 1 - \sum_{k = 0}^{m} P_{k}^{*} . \end{matrix}

(5)

Válasszuk tehát

m

-et először

0

-nak, és növeljük

m

-et addig, amíg a fenti kifejezés értéke kisebb nem lesz

ϵ

-nál. Ahol megállunk, az lesz a keresett

m

1. feladat. Igazoljuk a

(4)

kifejezés helyességét!

2. feladat. Póbáljuk meg megadni az Erlang által eredetileg levezetett formulát! A feladat csupán abban különbözik a fent bemutatott esettől, hogy a telefonálók száma tetszőleges.

3. Az Internet egy modellje

Egészen 1989-ig azt gondolták, hogy az említett Erlang-formula alkalmazható az Internet esetében is. 1989 augusztusában azonban a Bellcore helyi Ethernet hálózatán olyan mérési eredményeket kaptak, amelyek ellentmondtak a klasszikus modellek jóslatainak. Ennek bemutatása előtt tekintsük át, hogyan lehet egy számítógépes hálózat működését elképzelni.
Egy TCP nevű program a továbbítandó adatokat először kis csomagokra bontja, amelyek fejlécébe (mint egy postai levelezőlapra) beírja a küldő és a feladó címét, a feladás időpontját, és még néhány további adatot, majd sorban elküldi a csomagokat. Ha egy csomag sikeresen megérkezett, akkor a címzett visszaküld egy nyugtát a csomagról. Ha a TCP egy adott idő múlva még mindig nem kapott nyugtát egy csomagról, akkor azt a csomagot ismét elküldi.
Az Interneten levő csomagok központokon (routereken) keresztül haladnak a címzett számítógép felé. A router a beérkező csomagokat egymás után, egyesével továbbítja a megfelelő irányba. Ha egyszerre több csomag érkezik, akkor a csomagoknak az érkezés sorrendjében sorba kell állniuk. A router tárolókapacitása azonban véges, és így amelyik csomag már nem fér be a sorba, azt kénytelen eldobni. Ez a csomagvesztés jelzi a TCP számára, hogy túllépte a rendelkezésre álló kapacitást (sávszélességet).
Optimálisan akkor működik a TCP, ha éppen a rendelkezésre álló sávszélességet használja fel. A TCP által a hálózatból lefoglalt kapacitást a kiküldött adatmennyiség, valamint a küldés és az érkezés időkülönbségének hányadosa adja meg. Az optimális sávszélesség azonban minden pillanatban változhat, hiszen nem tudni, hogy egy adott időpillanatban hány másik TCP próbálja meg ugyanazt a vonalat használni.
A TCP ezért dinamikusan megpróbálja meghatározni a rá jutó kapacitást. Számos TCP verzió létezik, és ezek főként az optimalizációs algoritmusban térnek el egymástól. A TCP Reno verziója például ‐ erősen leegyszerűsítve ‐ először exponenciálisan növeli a hálózatba kiküldött csomagok számát, majd az első csomagvesztés után megfelezi a csomagküldés sebességét; ezután már csak lineárisan növeli a sebességet, majd csomagvesztés után ismét felez (3. ábra).

3. ábra. A TCP (Reno) csomagküldési algoritmusának sematikus váza
A klasszikus telefonhálózat és az Internet működését összehasonlítva látható, hogy míg a telefonhálózat esetén minden telefonáló csak egy előre meghatározott sávszélességet használ, addig a számítógépes hálózatokban a TCP a maximális rendelkezésére álló kapacitást megpróbálja kihasználni. A másik jelentős különbség a két hálózat között, hogy míg egy telefonvonal az egész beszélgetés alatt biztosított a két fél között, addig két számítógép között az adatok kis csomagokban, szakaszosan érkeznek.

4. Korrelációk

Az említett különbségekből még nem feltétlenül következne, hogy a két rendszert nem lehet ugyanazzal a modellel leírni. A mozipénztár előtti sor és a telefonhálózatban kialakuló sor is különbözik, mégis nagyon jól leírja mindkettőt az Erlang-formula. Lássuk tehát, hogy hogyan lehet mennyiségileg vizsgálni a két hálózat közötti különbséget.
Legyen

{X_{i}; i \in N}

egy véletlen sorozat, például

X_{i}

legyen a telefonálók, vagy az Internetben levő csomagok száma az

i

-edik

Δ t

időintervallumban. Definiáljuk a következő, úgynevezett korrelációs függvényt:

\begin{matrix} c (k) = 〈 (X_{i} - 〈 X_{i} 〉) (X_{i + k} - 〈 X_{i} 〉) 〉 \end{matrix}

(6)

ahol

〈 〉

i

szerinti átlagolást jelenti. Például

X_{i}

-re:

\begin{matrix} 〈 X_{i} 〉 = {lim}_{n \to \infty}^{} \frac{1}{n} \sum_{i = 0}^{n} X_{i} . \end{matrix}

(7)

c (k)

korrelációs függvény szemléletesen azt mutatja meg, hogy mennyire emlékszik a rendszer egy adott pillanatban a

k

időintervallummal korábbi eseményre. Ha

c (k) = 0

akkor a két esemény között nincs korreláció.
A ,,klasszikus'' telefonhálózatok modellezése során azt tapasztalták, hogy a korrelációs függvény nagyon nagy

k

-ra exponenciálisan csökken, azaz

\begin{matrix} c (k) \sim a^{| k |}, ha k \to \infty, 0 < a < 1. \end{matrix}

(8)

Az exponenciális függvény nagyon gyorsan csökken, s emiatt a rendszerre jellemző egy karakterisztikus idő, ami alatt gyakorlatilag teljesen elveszti a memóriáját. Ezzel szemben a korábban említett Bellcore-féle mérés során azt találták, hogy az Internet forgalom esetén a korrelációs függvény sokkal lassabban, csupán hatványfüggvény szerint csökken:

\begin{matrix} c (k) \sim | k |^{- β}, ha k \to \infty, \end{matrix}

(9)

ahol

0 < β < 1

. Fontos a kitevő értéke is, ugyanis

β

ilyen értékei mellett a korrelációs függvény összege végtelen:

\begin{matrix} \sum_{k = k_{0}}^{\infty} c (k) = \infty . \end{matrix}

(10)

Ezt úgy lehet értelmezni, hogy a rendszer tetszőlegesen hosszú idő után sem veszti el a memóriáját, nincs olyan karakterisztikus ideje, ami például a klasszikus telefonhálózatokra jellemző.

5. Fluktuációk

A korrelációs függvény viselkedéséből egy másik fontos tulajdonságot is levezethetünk. Osszuk az

X_{i}

sorozatot

m

méretű, nem átfedő blokkokba, és tekintsük azt az új

{X_{j}^{(m)}; j \in N}

sorozatot, ami ezeknek az új blokkoknak az átlagából áll:

\begin{matrix} X_{j}^{(m)} = \frac{1}{m} \sum_{i = j m}^{(j + 1) m - 1} X_{i} . \end{matrix}

(11)

\begin{matrix} {\underset{︸}{X_{0} X_{1} ... X_{m - 1}}}_{X_{0}^{(m)}}^{} {\underset{︸}{X_{m} X_{m + 1} ... X_{2 m - 1}}}_{X_{1}^{(m)}}^{} ... \end{matrix}

Ez egyenértékű azzal, mintha időegységünket eredetileg

Δ t

helyett

m Δ t

-nek választottuk volna.
A korrelációs függvény mellett vezessünk be egy másik mennyiséget is, ami azt mutatja meg, hogy az

X_{i}^{(m)}

mennyiség mennyire ingadozik az átlagértéke körül:

\begin{matrix} σ {(m)}^{2} = 〈 {(X_{i}^{(m)} - 〈 X^{(m)} 〉)}^{2} 〉 . \end{matrix}

(12)

Ezt a mennyiséget szórásnégyzetnek nevezik, és ‐ mint a definíciókból látható ‐ megegyezik

c^{(m)} (0)

-lal. A definíciók felhasználásával, és rövid számolás után kifejezhetjük

σ {(m)}^{2}

-et az eredeti véletlen sorozat korrelációs függvényével:

\begin{matrix} σ {(m)}^{2} = \frac{1}{m} c (0) + 2 \frac{1}{m^{2}} \sum_{k = 1}^{m - 1} (m - k) c (k) . \end{matrix}

(13)

Eredményünket megvizsgálva az adódik, hogy ha

c (k)

exponenciálisan, vagy

β \geq 1

kitevőjű hatványfüggvény szerint csökken, akkor nagy

m

esetén az első tag fog dominálni, ezért

σ {(m)}^{2} \sim m^{- 1}

. Ha viszont

c (k) \sim | k |^{- β}

, és

0 < β < 1

, akkor a második tag dominál, és

σ {(m)}^{2} \sim m^{- β}

, azaz az időskála növelésével a szórásnégyzet sokkal lassabban fog csökkenni, mint azt a klasszikus modell jósolja.

3. feladat. Igazoljuk a

(13)

kifejezés helyességét!

6. Önhasonlóság

Az eddigiekből sejthető, hogy a rendszert igazából egyetlen paraméter, a

β

kitevő jellemzi. Az ezen alapuló modellek is hamar megszülettek. Az alapötlet az időegység újraválasztásán alapul, amit például úgy lehet elvégezni, mint azt az előző fejezetben bemutattuk.
A természetben, a mindennapi életben máshol is gyakran előfordulnak olyan objektumok, amelyek különböző mérettartományokban ‐ bizonyos értelemben ‐ hasonlítanak egymásra. Ezeket az objektumokat általában fraktáloknak szokták nevezni.
Véletlen folyamatok, mint például az Internet forgalom esetében, kissé bonyolultabb a helyzet, ugyanis maga az

X_{i}

sorozat ‐ véletlen folyamatról lévén szó ‐ nem lehet önhasonló, statisztikus tulajdonságai ‐ mint például a korrelációs függvénye ‐ azonban már lehet az. Belátható például, hogy a blokkosítással kapott

X_{j}^{(m)}

sorozat korrelációs függvénye szintén

| k |^{- β}

szerint változik.
Az önhasonlóságot sokféleképpen lehet definiálni. Az egyik lehetséges definíció például, hogy

X_{i}

önhasonló, ha minden

m

-re

\begin{matrix} X_{i} =_{}^{d} m^{- H} \sum_{k = i m}^{(i + 1) m - 1} X_{k}, \end{matrix}

(14)

ahol

=_{}^{d}

azt jelöli, hogy a jobb- és a baloldal minden statisztikus tulajdonsága megegyezik.
Az Internet vázlatosan ismertetett modelljében azt tapasztaljuk, hogy különböző mennyiségek hatványfüggvény szerint változnak. A modellt tanulmányozók egyik fontos célkitűzése az, hogy kapcsolatot találjanak az egyes hatványfüggvények kitevői között, és meghatározzák a független paraméterek számát. Belátható például, hogy

H = 1 - β / 2

, azaz a két paraméter nem független egymástól.

7. Eloszlások

Arra vonatkozóan, hogy mi okozza a fent bemutatott önhasonlóságot többféle magyarázat született. Az egyik legelfogadottabb elmélet szerint a számítógépen található fájlok méretében, illetve a felhasználók viselkedésében kell keresni az okot.
Legyen

f (x) Δ x

annak a valószínűsége, hogy egy szamítógépen egy véletlenszerűen kiválasztott fájl mérete az

[x, x + Δ x [

intervallumba esik. Az

f (x)

függvényt eloszlásfüggványnek hívják. Mérések azt mutatják, hogy

f (x) \sim x^{- α}

, azaz a fájlméretek eloszlása szintén hatványfüggvény szerint csökken. A fentiek analógiájára definiálhatjuk azt az eloszlásfüggvényt, ami megadja, hogy a felhasználó (a program, az alkalmazás) milyen valószínűséggel várakozik

t

ideig. A mérések szerint ez is hatványszerű viselkedést követ.
Mindez egy tételen keresztül kapcsolódik az önhasonlóság forgalmához. A tétel úgynevezett ON/OFF folyamatokról szól. Az ON/OFF folyamat olyan forgalmat jelent, amikor a forgalmat generáló forrásnak mindössze két állapota lehetséges: bekapcsolt (ON) vagy kikapcsolt (OFF). A bekapcsolt és kikapcsolt állapotok váltakozva követik egymást, és az egyes állapotokban véletlenszerű ideig tartózkodik a rendszer.

4. ábra. Két ON/OFF folyamat, és normált összegük
A tétel szerint, ha olyan ON/OFF folyamatokat összegzünk (4. ábra), amelyekben az ON vagy az OFF állapotban tartózkodás valószínűségeloszlása hatványszerű viselkedést mutat, akkor az eredő forgalom önhasonló lesz.
Az Internet forgalmát tehát e szerint a modell szerint sok-sok párhuzamos, egymástól független ON/OFF folyamat összegeként lehet elképzelni, ahol az ON vagy az OFF folyamat eloszlása hatványfüggvényt követ. A kutatók többségének véleménye szerint ezek az ON állapotok az Internet felhasználói által indított fájl-letöltéseknek feleltethetők meg, az OFF állapotok pedig az ezek közötti szüneteknek. Hozzá kell tennünk, hogy nemrégiben olyan eredmények is születtek, amelyek azt mutatják, hogy a TCP önmagában, hatványszerű fájl-eloszlás nélkül is képes önhasonló forgalmat generálni.

Irodalom

*	[1]Eötvös Loránd Tudományegyetem Fizikus Diákkör: Bevezetés a véletlen folyamatok elméletébe és alkalmazásába, Eötvös Loránd Fizikai Társulat, 1979.

*	[2]M. E. Crovella and A. Bestavros: Self-Similarity in World Wide web Traffic: Evidence and Possible Causes, IEEE/ACM Transactions on Networking, 1997.

*	[3]Murad S. Taqqu, Walter Willinger and Robert Sherman: Proof of a Fundamental Result in Self-Similar Traffic Modeling, Computer Communication Review, 27, 1997.

Fekete Attila

ELTE Komplex Rendszerek Fizikája Tanszék

és Kommunikációs Hálózatok Laboratóriuma
e-mail: fekete@ector.elte.hu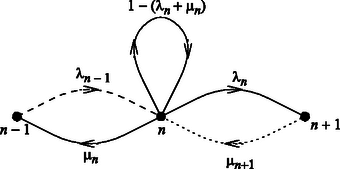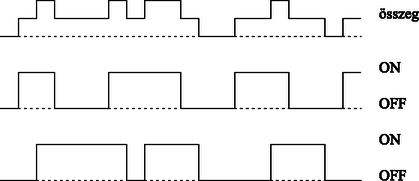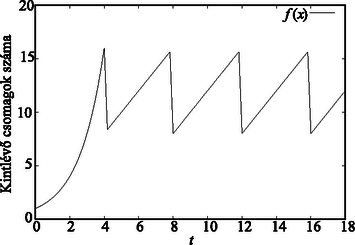

¹Feltesszük, hogy a mozipénztárnál senki sem tolakszik előre, azaz aki előbb érkezett, az előbb is kerül sorra.

² $ε$ valamilyen előre (mondjuk a szerződésben) meghatározott nagyon kicsi szám.

³Akárhányan is telefonáltak a kezdőpillanatban.