Cím: A matematika és fizika totó eredménye
Füzet: 2001/március, 172 - 174. oldal  PDF  |  MathML 
Témakör(ök): Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A múlt havi számunkban közreadtuk a 2000. évi Téli Ankét totó-kérdéseit. A telitalálatos szelvény:

X,2,1X,2,X2,1,X,X,X,21,X.
Az alábbiakban rövid útmutatást adunk a feladatok megoldásához.
 
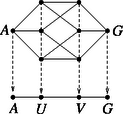
1. A kocka hálózatát átalakítva az eredetivel ekvivalens bolyongási feladatot kapunk, ha az A-val szomszédos csúcsokat U-ban, a G-vel szomszédosakat pedig V-ben egyesítjük úgy, hogy U-ból 23, V-ből pedig 13 a továbblépés valószínűsége. Ha p jelöli annak a valószínűségét, hogy U-ból indulva előbb jutunk G-be, mint A-ba, akkor a szimmetria miatt q=1-p annak a valószínűsége, hogy V-ből indulva előbb jutunk G-be, mint A-ba. Így p=23q, ahonnan p=25.
 
2. Az adatok (a Nap és a Hold tömege, illetve a távolságuk) táblázatból kikereshető számértékeinek felhasználásával közvetlenül adódik, hogy a Föld sokkal nagyobb erőt fejt ki a Napra, mint a Holdra.
Ehhez az eredményhez ,,fejben'' is eljuthatunk, ha figyelembe vesszük a következő közismert tényeket. A Nap és a Hold látószöge (a Földról nézve) gyakorlatilag ugyanakkora, hiszen 1999-ben a Hold éppen eltakarta a Napot. A Nap és a Hold felszíne tehát ugyanolyan arányban áll egymással, mint a Földtől mért távolságaik négyzete. Emiatt ha a sűrűségük egyforma lenne, akkor a gravitációs vonzóerők aránya éppen a két égitest sugarának hányadosával lenne egyenlő. Ez az arány erősen a Nap javára billenti a mérleget, s ezen az erős aszimmetrián az sem segít, hogy a Nap sűrűsége egy kicsit kisebb, mint a Holdé.
 
3. A betétek sorozata, fn, Fibonacci-típusú sorozat, amelyről ismert, hogy
fnfn-1→γ≈1,61803...,
ahol γ az aranymetszés aránya, az x2-x-1=0 egyenlet pozitív gyöke.
fn-1≈106:γ≈618033,9887miattfn-1=618034
választással és az fn-2=fn-fn-1 rekurzióval ,,visszafelé'' számolva a sorozat tagjait fn-18=144, fn-19=154, fn-20=-10, így n-19≥1, azaz n≥20, másfelől n-20≤0, azaz n≤20. Így n=20, f1=154 és f2=144.
 
4. A homok lepergése önmagában is bonyolult folyamat, amelyet a homokóra függőleges mozgása még bonyolultabbá tesz. Egyszerű elméleti megfontolásokkal nem lehet sem a sietésre, sem pedig a késésre következtetni, a ténylegesen elvégzett kísérletek pedig azt mutatták, hogy mindkét eset előfordulhat.
 
5. Az ábra hasonlóságainak felhasználásával könnyen megmutatható, hogy a körök sugarai mértani sorozatot alkotnak, így r=5⋅45=15cm.
 
6. A forráshoz az szükséges, hogy a folyadék hőmérsékletének megfelelő telített gőz nyomása meghaladja a folyadék nyomását. Zárt tartály és lassú melegítés esetén a folyadék feletti légtérben levegő és telített gőz található, ezek együttes nyomása (és ezzel együtt a folyadék nyomása is) mindig nagyobb, mint a telített gőz nyomása az esetlegesen képződő buborékokban. Ilyen buborékok tehát nem is jöhetnek létre, a folyadék sosem jön forrásba, hanem lassan, fokozatosan alakul át légnemű halmazállapotúvá.
 
7. Legalább 99-en biztosan megmenekülhetnek, a leghátul állónak pedig erre 12 esélye van. Ha a leghátsó az előtte álló 99 sapka közül pl. a fehérek számának paritását mondja ‐ pl. ,,fehér''-t mond, ha ez a szám páros ‐ akkor a látható sapkák és az addig elhangzottak ismeretében minden további elítélt meg tudja mondani, milyen színű sapka van a fején.
 
8. A gömb tükröző részén visszaverődő fény fotonjainak a gömb középpontjára vonatkoztatott impulzusnyomatéka nem változik az ,,ütközés'' során, ezek a fotonok tehát nem fejtenek ki forgatónyomatékot a gömbre. A fekete felületen elnyelődő fény viszont el akarja forgatni az UFO-t, méghozzá úgy, hogy minél kevesebb fekete részt érjen napfény. Amikor a tükröző oldalát fordítja a Nap felé, az a forgás szempontjából stabil egyensúlyi helyzet, a fordított állás pedig instabil.
 
9. A B. 3401. feladat II. megoldása szerint (lásd e szám 162‐163. oldalait) elegendő egyenlő tömegű csomagok esetén megtalálni a maximálisan elszállítható terhet, ehhez pedig az I. megoldás h(x) függvényének a felső határát kell megkeresni. A 3x és 11x egész értékeit vizsgálva h(x) felső határa 107, így a maximális elszállítható teher 14-107=887 tonna, 88+7 maradéka 3-mal osztva 2.
 
10. 99 méréssel biztosan ki tudjuk választani a legkönnyebbet, hiszen mindegyik méréssel kiválaszthatunk egy nehezebbet, s azt kidobva egyesével fogyaszthatjuk a még esélyes golyók számát. Meglepő, de ennél hatékonyabb eljárást nem ismerünk!
 
11. A c/r arány ‐ meglepő módon ‐ tetszőlegesen nagy lehet! Az alábbi eljárással egy adott (c,r) kertből egy megfelelő (c',r') kert készíthető úgy, hogy
c'r'=cr+13.

Tekintsünk egy 1 méter sugarú kört és ezen az A0, A1, A2 pontokat, majd a kert minden X virágából mérjük fel az XX1→=A0A1→ és az XX2→=A0A2→ vektorokat, és az Xi pontba ültessük az X-szel azonos fajtájú virágot. Így a kert két eltolt példányát kapjuk, amelyre teljesülnek a feltételek. Végül ha X rezeda, akkor az X, X1, X2 hármas ‐ egységnyi sugarú ‐ körülírt körének a középpontjába ültessünk egy cikláment.
Az új kertben r'=3r rezeda és c'=3c+r ciklámen lesz, így c'r'=cr+13, így a cr arány valóban tetszőlegesen nagy lehet.
 
Megjegyzés. Az A0A1→, A0A2→ vektorokat úgy kell fölvennünk, hogy ne kerüljön egy helyre két virág, és egyetlen ciklámen körül se legyen 3-nál több rezeda. Könnyen látható, hogy így csak véges sok vektort zárunk ki minden egyes alkalommal, így a megfelelő A0Ai→ vektorok mindig megadhatók.

 
12. A klasszikus fizikában a mozgó hullámforrás esetén a Doppler-effektusánál csak a hullámforrásnak a megfigyelő irányába eső sebességkomponense számít, így az éppen merőlegesen mozgó fényforrás színe változatlan maradna. Nagyon nagy sebességeknél azonban a relativisztikus Doppler-formulát kell alkalmaznunk, amely szerint egy ,,merőlegesen'' mozgó fényforrás fényének frekvenciája
f'=f1-v2c2<f,
az eredetileg zöld színű fény tehát a vörös felé tolódik el. (Ez a transzverzális Doppler-effektusnak nevezett jelenség.)
 
13. A játékot az első játékos nyeri, mégpedig 4-gyel és 5-tel kezdve is nyerhet. Egyesével haladva rendre kiértékelhetők a kezdőhelyzetek, és azt találjuk, hogy a játék kimenetelét tekintve a kezdőhelyzetek sorozata periodikus, a periódus hossza pedig 32 (és nem 11). Mivel 111=3⋅32+15 és 15 zseton esetén ‐ a lépésismétlés korlátozása miatt ‐ a 4 és az 5 is nyerő kezdőlépés, innen kapjuk az állítást.
 

Megjegyzés. Balszerencsés vagy szerencsés, mindenesetre a 13. számú kérdéshez méltó, hogy a feladat kérdésére sokan úgy válaszolhattak jól, hogy nem tudták, mi az igazság. Elsietett elemzés ugyanis azt látzik mutatni, hogy a nyerő helyzetek sorozata 11 szerint periodikus. Eszerint értékelve az első játékos nyeri a játékot, de nyerő lépése nem a 4 és nem is az 5. Helyesen játszva tehát ‐ okoskodtak sokan ‐ nem kezdhet sem 4-gyel, sem pedig 5-tel, A formális logika következtetési szabályai szerint tehát az első két állítás igaz, hiszen az előtagjuk hamis.

 
13 + 1. Ez a probléma szerepel a kitűzött feladatok között, részletes megoldását ezért csak később közöljük. Itt most csak annyit árulunk el, hogy Joe partra lépésének helye és az aranyrög közötti x távolságot célszerű független változónak választani, s ennek függvényében keresni a teljes haladási idő minimumát.