Cím:	2000. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldása
Szerző(k):	Károlyi Gyula
Füzet:	2001/február, 66 - 77. oldal	PDF  |  MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd), Matematika, Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   1. Az $A\left(\mathrm{0,}0\right)$, $B\left(n\mathrm{,}0\right)$, $C\left(n\mathrm{,}n\right)$ és $D\left(\mathrm{0,}n\right)$ pontok által meghatározott négyzet határán és belsejében elhelyezkedő rácspontokat pirosra vagy zöldre színezzük úgy, hogy a négyzetbe eső valamennyi egységoldalú rácsnégyzetnek pontosan két csúcsa legyen piros. Hányféleképpen tehetjük ezt meg?   Megoldás. A szóban forgó rácspontok $n+1$ sorban és $n+1$ oszlopban helyezkednek el. Nevezetesen, az $i$-edik sor ($0\le i\le n$) azokat a rácspontokat tartalmazza, amelyeknek a második koordinátája $i$. Hasonlóképpen, az $i$-edik oszlop azokból a rácspontokból áll, amelyek első koordinátája $i$. Két rácspontot szomszédosnak fogunk hívni akkor, ha ugyanabban a sorban vagy oszlopban egymás mellett helyezkednek el. Az $\left(i\mathrm{,}j\right)$ pont szomszédai tehát az $\left(i-\mathrm{1,}j\right)$, $\left(i+\mathrm{1,}j\right)$, $\left(i\mathrm{,}j-1\right)$ és $\left(i\mathrm{,}j+1\right)$ pontok, amennyiben ezek is az $ABCD$ négyzet pontjai. Nyilván jó színezését kapjuk a pontoknak akkor, ha minden sorban felváltva színezzük pirosra és zöldre az egymást követő pontokat. Az egyes sorokat ekkor egymástól függetlenül kétféleképpen színezhetjük, ezért az ilyen színezéseknek a száma $2^{n+1}$. Ugyanilyen megfontolásból lesz jó az a $2^{n+1}$ színezés is, ahol az egyes oszlopokban követik egymást felváltva a piros és zöld pontok. Mivel a pontokat kétféleképpen lehet úgy kiszínezni, hogy sem a sorokban, sem az oszlopokban nincs két szomszédos azonos színű pont, ezért így összesen $\begin{array}{c}{\displaystyle 2^{n+1}+2^{n+1}-2=2^{n+2}-2}\end{array}$ jó színezést találtunk. Megmutatjuk, hogy a fentieken kívül nincs más jó színezés. Ehhez tegyük fel először azt, hogy a pontokat megszíneztük a kívánt módon, és valamelyik oszlopban ‐ mondjuk az $i$-edikben ‐ van egymás mellett két azonos színű szomszédos pont. Legyenek ezek $\left(i\mathrm{,}j\right)$ és $\left(i\mathrm{,}j+1\right)$. Ekkor az $\left(i-1\right)$-edik és az $\left(i+1\right)$-edik oszlopban is található egymás mellett két azonos színű pont. Nevezetesen az $\left(i-\mathrm{1,}j\right)$, $\left(i-\mathrm{1,}j+1\right)$, $\left(i+\mathrm{1,}j\right)$, $\left(i+\mathrm{1,}j+1\right)$ pontok mind azonos színűek, és egyben az $\left(i\mathrm{,}j\right)$, $\left(i\mathrm{,}j+1\right)$ pontoktól eltérő színűek kell, hogy legyenek. Indukcióval könnyen ellenőrizhető ezután, hogy az $\left(i-k\mathrm{,}j\right)$, $\left(i-k\mathrm{,}j+1\right)$, $\left(i+k\mathrm{,}j\right)$, $\left(i+k\mathrm{,}j+1\right)$ pontok színe az $\left(i\mathrm{,}j\right)$, $\left(i\mathrm{,}j+1\right)$ pontokéval megegyező, ha $k$ páros, illetve azokétól eltérő, ha $k$ páratlan. Tegyük fel most még azt is, hogy valamelyik sorban ‐ mondjuk a $j\text{'}$-edikben ‐ is van egymás mellett két azonos színű pont: $\left(i\text{'}\mathrm{,}j\text{'}\right)$ és $\left(i\text{'}+\mathrm{1,}j\text{'}\right)$. Az előbbihez hasonló gondolatmenettel (vagy egyszerűbben: szimmetria okokra hivatkozva) megállapíthatjuk, hogy minden $k$-ra az $\left(i\text{'}\mathrm{,}j\text{'}-k\right)$, $\left(i\text{'}+\mathrm{1,}j\text{'}-k\right)$, $\left(i\text{'}\mathrm{,}j\text{'}+k\right)$, $\left(i\text{'}+\mathrm{1,}j\text{'}+k\right)$ pontok azonos színűek. A fentiek szerint az $\left(i\text{'}\mathrm{,}j\right)$ pont színe meg kell, hogy egyezzen mind az $\left(i\text{'}\mathrm{,}j+1\right)$, mind az $\left(i\text{'}+\mathrm{1,}j\right)$ pont színével. Ez azonban egy jó színezésben nem történhet meg, hiszen a felsorolt három pont éppen egy egységoldalú rácsnégyzet három csúcsa. Ez az ellentmondás igazolja azon állításunkat, miszerint minden jó színezésben vagy az oszlopokban, vagy a sorokban váltakozó színű pontok követik egymást. A kérdéses színezések száma tehát $2^{n+2}-2$.   2. Legyen $ABC$ szabályostól különböző háromszög, $P$ pedig a síknak a háromszög csúcsaitól különböző pontja. Jelöljék $A_P$, $B_P$ és $C_P$ rendre az $AP$, $BP$ és $CP$ egyeneseknek az $ABC$ háromszög köré írt körrel vett második metszéspontjait. Mutassuk meg, hogy a síknak pontosan két olyan $P$ és $Q$ pontja van, hogy az $A_P{B}_P{C}_P$ és $A_Q{B}_Q{C}_Q$ háromszögek szabályosak, továbbá, hogy a $PQ$ egyenes áthalad az $ABC$ háromszög köré írt kör középpontján.   Az első két megoldás a körre vonatkozó inverzió fogalmára támaszkodik, ezért röviden összefoglaljuk ennek a transzformációnak legfontosabb tulajdonságait. Ha adott a síkon egy $O$ középpontú, $r$ sugarú $k$ kör, akkor a $k$ körre vonatkozó inverzió a sík $O$-tól különböző pontjainak az a leképezése, amely tetszőleges $P$ ponthoz az $OP$ félegyenes azon $P\text{'}$ pontját rendeli hozzá, amelyre $OP\cdot OP\text{'}=r^2$. Ha az $A$ pont (vagy alakzat) képe $B$, akkor a $B$ ponté (alakzaté) éppen $A$. A leképezés tehát egy-egyértelmű, a $k$ pontjait helyben hagyja, $k$-n belüli pontokat pedig $k$-n kívüli pontokba visz, és fordítva. Ha egy kör az $O$ pontot elkerüli, akkor a körvonal képe egy, az $O$-t szintén elkerülő körvonal, egy $O$-n áthaladó $k_1$ körvonal képe pedig egy $O$-ra nem illeszkedő egyenes: a $k$ és $k_1$ körök hatványvonala. Fontos tulajdonsága az inverziónak a szögtartás: ha $k_1$ és $k_2$ egy-egy körvonal (elfajuló esetben $O$-ra nem illeszkedő egyenes), akkor a $k_1\text{'}$ és $k_2\text{'}$ körök ugyanolyan szög alatt metszik egymást, mint a $k_1$ és $k_2$ körök. (Két egymást metsző kör által bezárt szög alatt közös pontjukban húzott érintőik hajlásszögét értjük.) Speciálisan, ha a $k_1$ kör $k$-t merőlegesen metszi, akkor $k\text{'}=k$ miatt $k_1\text{'}$ is merőlegesen metszi $k$-t, méghozzá ugyanabban a két pontban, ezért $k_1\text{'}=k_1$. Ezek után lássuk először a legkevesebb diszkussziót igénylő megoldást.   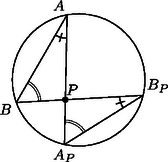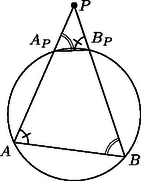I. Megoldás. Ha $P$ az $ABC$ háromszög köré írható $k$ körön van, akkor $A_P=B_P=C_P=P$, és így az $A_P{B}_P{C}_P$ háromszögről nem beszélhetünk. Az egyazon húrhoz tartozó kerületi szögek egyenlőségéről szóló tételre hivatkozva az 1. ábráról leolvasható, hogy az $A_P{B}_{P}P$ háromszög hasonló a $BAP$ háromszöghöz, függetlenül attól, hogy $P$ a $k$ körön belül, vagy azon kívül helyezkedik-e el. Ezért $\frac{A_P{B}_P}{B_{P}P}=\frac{BA}{AP}$, és hasonló módon $\frac{C_P{B}_P}{B_{P}P}=\frac{BC}{CP}$.             1. ábra   Az $A_P{B}_P=B_P{C}_P$ feltétel tehát ekvivalens az $\frac{AP}{CP}=\frac{AB}{CB}$ feltétellel, vagyis azzal, hogy $P$ az $A$ és $C$ pontokhoz, valamint az $\frac{AB}{CB}$ arányhoz tartozó Apollóniusz-körnek $k$-ra nem illeszkedő pontja. (Abban a speciális esetben, amikor $AB=CB$, ez az Apollóniusz-kör elfajuló, és az $AC$ szakasz felező merőlegesével egyezik meg.) Ugyanígy kapjuk azt is, hogy az $A_P{B}_P=A_P{C}_P$ feltétel ekvivalens azzal, hogy $P$ a $B$ és $C$ pontokhoz, valamint az $\frac{BA}{CA}$ arányhoz tartozó Apollóniusz-körnek $k$-ra nem illeszkedő pontja. Az $A_P{B}_P{C}_P$ háromszög tehát pontosan akkor szabályos, ha $P$ az említett két Apollóniusz-kör ($k$-ra nem illeszkedő) közös pontja. 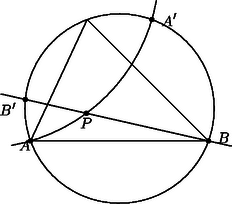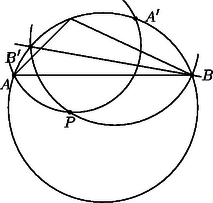Az $AC$ egyenes elválasztja az első Apollóniusz-kör $k$-val való, $B$-től különböző $B\text{'}$ metszéspontját a $B$ ponttól. Ugyanígy, a $BC$ egyenes elválasztja a második Apollóniusz-kör $k$-val való, $A$-től különböző $A\text{'}$ metszéspontját az $A$ ponttól. Következésképpen az $A$, $B$, $A\text{'}$, $B\text{'}$ pontok a $k$ körön ilyen sorrendben helyezkednek el (2. ábra), és ezért a két Apollóniusz-kör mind a $k$ körön belül, mind azon kívül egy-egy pontban metszi egymást. Pontosabban, a $k$-n kívüli metszéspont nem létezik abban az esetben, ha mind a két Apollóniusz-kör elfajuló, ez azonban pontosan akkor következik be, ha az $ABC$ háromszög szabályos. Ezzel a feladat első állítását beláttuk.       2. ábra   A második állítás bizonyítása azon az észrevételen alapul, hogy az említett Apollóniusz-körök a $k$ kört merőlegesen metszik. Ekkor ugyanis a szögtartás miatt a $k$-ra vonatkozó inverzió mind a két Apollóniusz-kört saját magába viszi, és ezért a körök metszéspontjainak képe az inverzió során ugyanez a két pont. Mivel a $k$ körön belüli pontok a $k$-n kívüli pontokba transzformálódnak, ez csak úgy lehetséges, ha az inverzió $P$-t és $Q$-t felcseréli. A $P$ és $Q$ pontok tehát egymásnak a $k$ körre vonatkozó inverz képei, ennek megfelelően a $PQ$ egyenes valóban áthalad a $k$ kör $O$ középpontján. Szimmetria okokból elegendő azt megmutatni, hogy az első Apollóniusz-kör (jelöljük ezt $k_1$-gyel) merőlegesen metszi $k$-t. Ez nyilvánvaló, ha $AB=CB$, egyébként pedig feltehetjük, hogy $\alpha =BAC\sphericalangle >BCA\sphericalangle =\gamma$. Legyen a $B$-ből induló belső szögfelező talppontja $T$, a külsőé $S$. A szögfelező-tétel értelmében $ST$ éppen a $k_1$ körnek az $AC$ egyenesre eső átmérője, amely tartalmazza az $A$ pontot is (3. ábra). 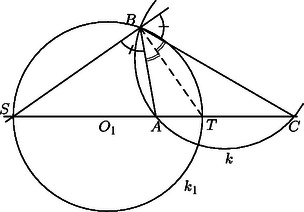    3. ábra   Ezért $SBT\sphericalangle =\frac{\pi }{2}$. Továbbá $\begin{array}{c}{\displaystyle TBO\sphericalangle =\frac{\beta }{2}-\left(\frac{\pi }{2}-\alpha \right)=\frac{\pi }{2}-\left(\pi -\left(\alpha +\frac{\beta }{2}\right)\right)=\frac{\pi }{2}-BTS\sphericalangle =BST\sphericalangle =SB{O}_1\sphericalangle \mathrm{,}}\end{array}$ ahol $O_1$ a $k_1$ kör középpontja. Ezért $\begin{array}{c}{\displaystyle O_{1}BO\sphericalangle =SBT\sphericalangle +TBO\sphericalangle -SB{O}_1\sphericalangle =\frac{\pi }{2}\mathrm{,}}\end{array}$ és éppen ezt akartuk bizonyítani.   II. Megoldás. Rögzítsük a pozitív forgásirányt úgy hogy az $A$, $B$, $C$ csúcsok ilyen sorrendben helyezkedjenek el a háromszög köré írt $k$ körön. Hogy kevesebb esetet kelljen megkülönböztetni, irányított szögekkel fogunk dolgozni. Két irányított szöget azonosnak tekintünk akkor, ha különbségük $2\pi$ egész számú többszöröse. Ha $X$, $Y$ a $k$ kör pontjai, akkor az $XY$ irányított ívhez tartozó (irányított) kerületi szöget jelölje $\phi \left(XY\right)$. Például $\phi \left(AB\right)=\gamma$, $\varphi \left(BC\right)=\alpha$ és $\varphi \left(CA\right)=\beta$ a háromszög szögei, ugyanakkor $\phi \left(BA\right)={180}^{\circ }-\gamma$. Azt mondjuk, hogy az $XY$ (irányított) szakasz a $P$ pontból $\varphi$ szög alatt látszik, ha $XPY\sphericalangle =\varphi$, ekkor az $YX$ szakasz $P$-ből $-\varphi$ szög alatt látszik. Az ilyen $P$ pontok összessége alkotja az $XY$ szakaszra támaszkodó $\varphi$ szögű látókörívet, ami $\varphi =\pi$ esetén a végpontjait nem tartalmazó $XY$ szakasszal, $\varphi =0$ esetén pedig az $XY$ egyenes $XY$ szakaszon kívül eső részével egyezik meg. Ennyi előkészület után most már rátérhetünk a megoldás lényegi részére. A $k$ körön nyilván nem helyezkedhet el megfelelő pont. Legyen tehát először $P$ a $k$ kör egy tetszőleges belső pontja, ekkor az $ABC$ és $A_P{B}_P{C}_P$ háromszögek azonos körüljárásúak. Az utóbbi háromszög tehát pontosan akkor szabályos, ha a $\varphi \left(A_P{B}_P\right)$, $\varphi \left(B_P{C}_P\right)$, $\varphi \left(C_P{A}_P\right)$ szögek közül legalább kettő (és persze akkor a harmadik is) ${60}^{\circ }$. Mármost $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle APB\sphericalangle ={180}^{\circ }-BAP\sphericalangle -PBA\sphericalangle ={180}^{\circ }-BA{P}_A\sphericalangle -B_{P}BA\sphericalangle =}\\ \hfill {\displaystyle {180}^{\circ }-\varphi \left(B{A}_P\right)-\varphi \left(B_{P}A\right)=\varphi \left(AB\right)+\varphi \left(A_P{B}_P\right)=\gamma +\varphi \left(A_P{B}_P\right)\mathrm{,}}\end{array}}}\end{array}$ Az $AB$, $B{A}_P$, $A_P{B}_P$ és $B_{P}A$ ívek ugyanis együtt éppen lefedik a $k$ kört, így a hozzájuk tartozó kerületi szögek összege pontosan ${180}^{\circ }$. Hasonlóképpen, $BPC\sphericalangle =\alpha +\varphi \left(B_P{C}_P\right)$ és $CPA\sphericalangle =\beta +\varphi \left(C_P{A}_P\right)$. Az $A_P{B}_P{C}_P$ háromszög tehát pontosan akkor szabályos, ha a $P$ pontból az $AB$, $BC$, $CA$ szakaszok rendre $\gamma +{60}^{\circ }$, $\alpha +{60}^{\circ }$, $\beta +{60}^{\circ }$ szögben látszanak. E három feltétel közül persze elég csak kettőt megkövetelni. Most már nem nehéz megmutatni, hogy a $k$ körön belül pontosan egy ilyen $P$ pont van. Az általánosság megszorítása nélkül feltehetjük, hogy $\alpha$, $\gamma <{120}^{\circ }$. Tekintsük most az $AB$ szakaszra támaszkodó $\gamma +{60}^{\circ }$ szögű ${\ell }_C$ látókörívet és a $BC$ szakaszra támaszkodó $\alpha +{60}^{\circ }$ szögű ${\ell }_A$ látókörívet, ezek tehát a megfelelő szakaszoknak a háromszöget tartalmazó oldalán helyezkednek el. A harmadik hasonló látókörívre is (amely már nem biztos, hogy az AC szakasznak a háromszöget tartalmazó oldalán helyezkedik el) szükségünk lesz később, ezt jelöljük ${\ell }_B$-vel. Hogy ez a két ív pontosan egy pontban metszi egymást, méghozzá a $k$ kör belsejében, a következőképpen igazolhatjuk. Először is vegyük észre, hogy mindkét látókörív a $k$ kör belsejében halad. Másodszor, $B$ közös végpontja mindkét ívnek. Ezért a két ívnek legfeljebb egy közös belső pontja lehet, és a metszéspont létrejöttének szükséges és elégséges feltétele az, hogy az ${\ell }_A$ ív a $BC$ oldallal, illetve az ${\ell }_C$ ív a $BA$ oldallal olyan szögeket zárjon be, amelyek összege $\beta$-t meghaladja (most kivételesen nem irányított szögektől beszélünk). Egyszerű számolással ellenőrizhető, hogy ez valóban így van. Azt is megállapíthatjuk, hogy lévén ekkor $CPA\sphericalangle =\beta +{60}^{\circ }$, ez a $P$ pont akkor esik az $ABC$ háromszög belsejébe, ha $\beta <{120}^{\circ }$, a háromszögön kívül helyezkedik el a $\beta >{120}^{\circ }$ esetben, ha pedig $\beta ={120}^{\circ }$, akkor az $AC$ oldalra illeszkedik. Összefoglalva tehát megállapíthatjuk, hogy a $k$ körön belül mindig pontosan egy ilyen pont van, méghozzá az $ABC$ háromszög belsejében, ha a háromszög minden szöge ${120}^{\circ }$-nál kisebb, annak határán, ha a háromszögnek van egy ${120}^{\circ }$-os szöge, illetve azon kívül, ha valamelyik szöge ${120}^{\circ }$-nál nagyobb. Ebből a $P$ pontból az $AB$, $BC$, $CA$ szakaszok rendre $\gamma +{60}^{\circ }$, $\alpha +{60}^{\circ }$, $\beta +{60}^{\circ }$ alatt látszanak. 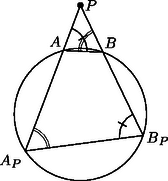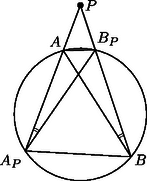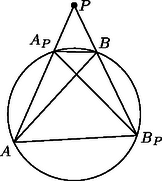Legyen most a $P$ pont a $k$ kör egy külső pontja. Az $APB\sphericalangle$ meghatározásához különböztessünk meg négy esetet annak megfelelően, hogy a $PA$ és $PB$ félegyeneseken a $P$, $A$, $A_P$, illetve $P$, $B$, $B_P$ pontok milyen sorrendben helyezkednek el (1. ábra). Megjegyezzük, hogy az irányított szögekkel való számolásnak az is előnye, hogy nem kell azzal foglalkoznunk, hogy ez a két félegyenes egymáshoz képest milyen helyzetű. Mind a négy esetben könnyen ellenőrizhető, hogy $\begin{array}{c}{\displaystyle APB\sphericalangle ={180}^{\circ }-BAP\sphericalangle -PBA\sphericalangle ={180}^{\circ }-\varphi \left(B{A}_P\right)-\varphi \left(B_{P}A\right)=}\end{array}$ $\begin{array}{c}{\displaystyle \left({180}^{\circ }-\varphi \left(B{A}_P\right)-\varphi \left(A_{P}A\right)\right)-\varphi \left(B_P{A}_P\right)=\varphi \left(AB\right)-\varphi \left(B_P{A}_P\right)=\gamma -\varphi \left(B_P{A}_P\right)\mathrm{.}}\end{array}$ Ugyanígy $BPC\sphericalangle =\alpha -\varphi \left(C_P{B}_P\right)$ és $CPA\sphericalangle =\beta -\varphi \left(A_P{C}_P\right)$. Mivel most az $A_P{B}_P{C}_P$ háromszög körüljárása ellentétes az $ABC$ háromszögével, ez a háromszög pontosan akkor szabályos, ha a $\varphi \left(B_P{A}_P\right)$, $\varphi \left(C_P{B}_P\right)$, $\varphi \left(A_P{C}_P\right)$ szögek közül legalább kettő (és persze akkor a harmadik is) ${60}^{\circ }$. Ezzel ekvivalens az, hogy a $P$ pontból az $AB$, $BC$, $CA$ szakaszok rendre $\gamma -{60}^{\circ }$, $\alpha -{60}^{\circ }$ és $\beta -{60}^{\circ }$ alatt látszanak. Jelölje az ennek megfelelő látóköríveket rendre ${\ell }_C\text{'}$, ${\ell }_A\text{'}$ és ${\ell }_B\text{'}$. Állítás. A $k$ körre vonatkozó inverziónál az ${\ell }_A$, ${\ell }_B$, ${\ell }_C$ ívek képe rendre ${\ell }_A\text{'}$, ${\ell }_B\text{'}$ és ${\ell }_C\text{'}$. Ebből azonnal következik, hogy a $k$ körön kívül is pontosan egy olyan $Q$ pont van, amelyre az $A_Q{B}_Q{C}_Q$ háromszög szabályos, mégpedig ez a pont a $P$ pont inverz képe. Probléma csak akkor lenne, ha $P$ egybeesne a $k$ kör középpontjával, ez azonban nem lehetséges, hiszen az $ABC$ háromszög nem szabályos. Egyúttal azt is megkaptuk, hogy a $k$ kör középpontja, valamint a $P$ és $Q$ pontok egy egyenesen vannak. Most már csak a fenti állítást kell igazolni. Ha a háromszög szögeire semmiféle megkötést nem teszünk, akkor szimmetria okok miatt nyilván elég annyit megmutatni, hogy ${\ell }_A$ inverz képe éppen ${\ell }_A\text{'}$. A bizonyítás azon az egyszerű észrevételen múlik, hogy az a két ív, amelynek pontjaiból az $XY$ (irányított) szakasz ${\varphi }_1$, illetve ${\varphi }_2$ szög alatt látszik, ${\varphi }_1-{\varphi }_2$ szöget zár be egymással. Ennek alapján a kerületi szögek tételéből következik, hogy mind az ${\ell }_A$ ív, mind az ${\ell }_A\text{'}$ ív ${60}^{\circ }$-os szöget zár be a $k$ körrel. Nem nehéz megmutatni, hogy az ${\ell }_A$ ív a $k$ körön belül, az ${\ell }_A\text{'}$ ív pedig azon kívül halad. A két ívnek ugyanazok a végpontjai, de nem egészítik ki egymást egyetlen körvonallá. Mivel az a két körvonal, amely a $k$-t a $B$ és $C$ pontokban egyaránt ${60}^{\circ }$-os szög alatt metszi, egymás inverz képe a $k$ körre nézve, a szóban forgó két ív is egymás inverze, és ezt akartuk bizonyítani.   III. Megoldás. (Béky Bence megoldása.) Az előző megoldások valamelyikét követve először is megállapítjuk, hogy valóban két ilyen pont létezik, méghozzá egy a háromszög köré írható körön belül (jelöljük ezt $P$-vel), a másik pedig a körön kívül (legyen ez $Q$). Vegyük most észre, hogy az $A_P{B}_P{C}_P$ háromszög körüljárása megegyezik az $ABC$ háromszögével, míg az $A_Q{B}_Q{C}_Q$ háromszögé azzal ellentétes. Található tehát egy, a $k$ kör $O$ középpontjára illeszkedő $e$ egyenes, amelyre az $A_P{B}_P{C}_P$ háromszöget tükrözve az $A_Q{B}_Q{C}_Q$ háromszöget kapjuk. Vizsgáljuk először azt az általános esetet, amikor $A_P$ különbözik a $B_Q$, $C_Q$ pontoktól, $B_P$ különbözik az $A_Q$, $C_Q$ pontoktól és $C_P$ is különbözik az $A_Q$, $B_Q$ pontoktól. Nem lehet, hogy például az $A_P{B}_Q$ egyenes egybeesik az $A_Q{B}_P$ egyenessel, mert ekkor $A_P=B_P$ lenne. Az $A_P{B}_Q$ egyenes tehát csak akkor lehet párhuzamos az $A_Q{B}_P$ egyenessel, ha egyben $e$-vel is párhuzamos. Ugyanez elmondható a másik két értelemszerűen felírt egyenespárról. Jelölje $A^{*}$, $B^{*}$ és $C^{*}$ rendre a $B_P{C}_Q$ és $B_Q{C}_P$ egyeneseknek, az $A_P{C}_Q$ és $A_Q{C}_P$ egyeneseknek, illetve az $A_P{B}_Q$ és $A_Q{B}_P$ egyeneseknek a metszéspontját. Az elmondottak szerint ezen egyenespárok közül legfeljebb egy lehet párhuzamos helyzetben, az $e$ egyenesre eső $A^{*}$, $B^{*}$, $C^{*}$ pontok közül tehát kettő biztosan létrejön. Feltehetjük, hogy az $A^{*}$ és $B^{*}$ pontok ilyenek. Világos, hogy $A^{*}$ és $B^{*}$ különböző pontok (4. ábra). 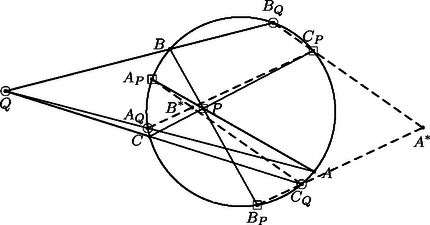    4. ábra   Tekintsük most a $k$ körbe írt $B{B}_Q{C}_{P}C{C}_Q{B}_P$ önmagát átmetsző hatszöget. Ennek $B{B}_Q$ és $C{C}_Q$ szemközti oldalai $Q$-ban, $B_Q{C}_P$ és $C_Q{B}_P$ szemközti oldalai $A^{*}$-ban, $C_{P}C$ és $B_{P}B$ szemközti oldalai pedig $P$-ben metszik egymást. Pascal tétele szerint tehát az $A^{*}$ pont illeszkedik a $PQ$ egyenesre (5. ábra). 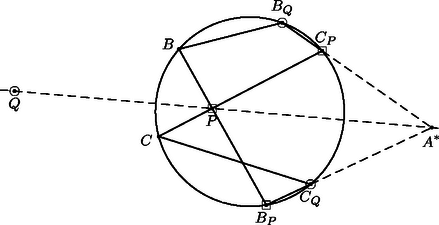    5. ábra   Hasonlóképpen belátható, ezúttal az $A{A}_Q{C}_{P}C{C}_Q{A}_P$ hatszögből kiindulva, hogy a $B^{*}$ pont is illeszkedik a $PQ$ egyenesre. A $PQ$ egyenes tehát egybeesik az $A^{*}{B}^{*}$ egyenessel, vagyis az $O$ ponton áthaladó $e$ egyenessel, ami bizonyítja az általános esetben a feladat második állítását. Tegyük fel végül, hogy mondjuk $B_P=C_Q=X$, ekkor az $e$-re való szimmetria miatt $B_Q=C_P=Y$, végül pedig $A_P=A_Q$ a $k$ körnek az a $Z$ pontja, amelyre az $XYZ$ háromszög szabályos. Világos, hogy $Z$ illeszkedik az $e$ egyenesre, $XY$ pedig merőleges arra. Ekkor az $B_P{C}_Q$ és $B_Q{C}_P$ egyenesek helyett tekintsük a $k$ körhöz annak $X$, illetve $Y$ pontjában húzott érintőjét, ez a két egyenes a $Z$ pontnak az $XY$-ra vonatkozó tükörképében metszi egymást. Jelöljük most ezt a pontot $A^{*}$-gal. A $B^{*}$, $C^{*}$ pontok ugyanúgy definiálhatók, mint az általános esetben, és ezúttal egybeesnek $Z$-vel. Az $A^{*}$ és $B^{*}$ pontok tehát most is az $e$ egyenest határozzák meg. Most már szinte szó szerint megismételhetjük az előző bekezdést azzal az apró módosítással, hogy most a $B{B}_Q{C}_{P}C{C}_Q{B}_P$ hatszög elfajuló abban az értelemben, hogy két-két szomszédos csúcsa egybeesik. Ezért a Pascal tétel alkalmazásánál a $B_P{C}_Q$ és $B_Q{C}_P$ egyenesek helyett éppen az előbb említett érintőket kell tekinteni.   Megjegyzések. 1. A feladat komplex számok segítségével viszonylag egyszerű számolás útján is megoldható. Ezt az utat választotta Gyenes Zoltán a második állítás bizonyításához. 2. Egy mélyebb matematikai eszközöket használó megoldást tartalmaz, és a feladat hátterére mutat rá Hraskó András cikke, amely a következő számunkban jelenik meg. 3. A harmadik megoldásból azonnal leolvasható, hogy az $A_P{B}_P{C}_P$ és $A_Q{B}_Q{C}_Q$ háromszögek a $PQ$ egyenesre szimmetrikusan helyezkednek el. Erre az eredményre az első megoldás ügyes folytatásával is eljuthatunk. Hogyan? Ennek az önmagában is szép feladatnak a megoldását már az olvasóra bízzuk.   3. Legyen $k$ nemnegatív egész szám, és tegyük fel, hogy az $a_1$, $a_2$, $\text{...}$, $a_n$ egész számok legalább $2k$ különböző maradékot adnak $\left(n+k\right)$-val osztva. Bizonyítandó, hogy a számok között van néhány, amelyek összege osztható $\left(n+k\right)$-val.   I. megoldás. Az általánosság megszorítása nélkül feltehető, hogy az $a_1$, $a_2$, $\text{...}$, $a_{2k}$ számok páronként különböző maradékot adnak $\left(n+k\right)$-val osztva. Tekintsük a következő $n+k$ különböző számot: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle b_1}& {\displaystyle =a_1\mathrm{,}{b}_2=a_1\mathrm{,}{b}_3=a_1+a_2}\hfill \\ \hfill {\displaystyle b_{3i+1}}& {\displaystyle =a_1+a_2+\text{...}+a_{2i}+a_{2i+1}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>0</mn><mo stretchy="false"><</mo><mi>i</mi><mo stretchy="false"><</mo><mi>k</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>, }}\\ \hfill {\displaystyle b_{3i+2}}& {\displaystyle =a_1+a_2+\text{...}+a_{2i}+a_{2i+2}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>0</mn><mo stretchy="false"><</mo><mi>i</mi><mo stretchy="false"><</mo><mi>k</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>, }}\\ \hfill {\displaystyle b_{3i+3}}& {\displaystyle =a_1+a_2+\text{...}+a_{2i}+a_{2i+1}+a_{2i+2}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>0</mn><mo stretchy="false"><</mo><mi>i</mi><mo stretchy="false"><</mo><mi>k</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>, }}\\ \hfill {\displaystyle b_j}& {\displaystyle =a_1+a_2+\text{...}+a_{j-k}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>3</mn><mi>k</mi><mo stretchy="false"><</mo><mi>j</mi><mo>≤</mo><mi>n</mi><mo stretchy="false">+</mo><mi>k</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>. }}\end{array}}}\end{array}$ Ha ezek között van olyan, amelyik osztható $\left(n+k\right)$-val, akkor mar készen is vagyunk. Ellenkező esetben pedig van a számok között kettő, mondjuk $b_s$ és $b_t$ ($s<t$) amelyik ugyanolyan maradékot ad $\left(n+k\right)$-val osztva. Ekkor $b_t-b_s$ nyilván osztható $\left(n+k\right)$-val. Azt kell már csak észrevennünk, hogy ez a különbség felírható az $a_1$, $a_2$, $\text{...}$, $a_n$ számok közül néhánynak az összegeként. Ha ugyanis ez nem így lenne, akkor valamilyen $k$-nál kisebb $i$-re $s=3i+1$ és $t=3i+2$, vagyis $b_t-b_s=a_{2i+2}-a_{2i+1}$ volna. Ez azonban feltételezésünk értelmében nem osztható $\left(n+k\right)$-val.   II. megoldás. Ugyanehhez a végeredményhez egy kissé eltérő kiindulással is eljuthatunk. Állítás. Tetszőleges $b_1$, $b_2$, $\text{...}$, $b_N$ egész számok esetén léteznek olyan $1\le i\le j\le N$ indexek, hogy a $b_i+b_{i+1}+\text{...}+b_j$ összeg osztható $N$-nel. Ez egyébként éppen a feladat állítása a $k=0$ esetben. A bizonyításhoz tekintsük $t=0$, $1$, $\text{...}$, $N$ esetén az $s_t=b_1+\text{...}+b_t$ összegeket, ahol $s_0=0$ az üres összeg. Az így felírt $N+1$ egész szám között biztosan van kettő, amelyik ugyanolyan maradékot ad $N$-nel osztva. Ha $s_k$ és $s_{\ell }$ ($0\le k<\ell \le N$) két ilyen összeg, akkor $s_{\ell }-s_k=b_{k+1}+b_{k+2}+\text{...}+b_{\ell }$ osztható $N$-nel. A feladatot ezután a következő módon vezethetjük vissza erre a speciális esetre. Az első megoldáshoz hasonlóan, most is feltehetjük, hogy az $a_1$, $a_2$, $\text{...}$, $a_{2k}$ számok páronként különböző maradékot adnak $\left(n+k\right)$-val osztva. Tekintsük a $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle b_1=a_1\mathrm{,}{b}_2=a_2-a_1\mathrm{,}{b}_3=a_1\mathrm{,}{b}_4=a_3\mathrm{,}{b}_5=a_4-a_3\mathrm{,}{b}_6=a_3\mathrm{,}\text{...}\mathrm{,}{b}_{3k}=a_{2k-1}\mathrm{,}}\\ \hfill {\displaystyle b_{3k+1}=a_{2k+1}\mathrm{,}{b}_{3k+2}=a_{2k+2}\mathrm{,}\text{...}\mathrm{,}{b}_{n+k}=a_n}\end{array}}}\end{array}$ számokat. Így éppen $N=n+k$ egész számot írtunk fel. A fenti állítás értelmében léteznek olyan $1\le i\le j\le N$ indexek, hogy $S=b_i+b_{i+1}+\text{...}+b_j$ osztható $N$-nel. Elegendő azt megmutatni, hogy $S$ felírható az $a_1$, $a_2$, $\text{...}$, $a_n$ számok közül néhánynak az összegeként. Ez egészen nyilvánvaló akkor, ha $i\ge 3k+1$, ebben az esetben ugyanis $\begin{array}{c}{\displaystyle S=a_{i-k}+a_{i-k+1}+\text{...}+a_{j-k}\mathrm{.}}\end{array}$ Ha $i\le 3k<j$, akkor legyen $i=3s+q$, ahol $0\le s<k$ és $1\le q\le 3$. Ekkor nyilván $\begin{array}{c}{\displaystyle S=A+a_{2s+3}+a_{2s+4}+\text{...}+a_{j-k}\mathrm{,}}\end{array}$ ahol $A=a_{2s+1}+a_{2s+2}$, $a_{2s+2}$, vagy $a_{2s+1}$ annak megfelelően, hogy $q$ értéke 1, 2, vagy pedig 3. Végül $j\le 3k$ esetén legyen $i=3s+q$, $j=3t+r$, ahol $0\le s\le t<k$ és $1\le q\mathrm{,}r\le 3$. Ekkor könnyen ellenőrizhető, hogy $\begin{array}{c}{\displaystyle S=A+a_{2s+3}+a_{2s+4}+\text{...}+a_{2t}+B\mathrm{,}}\end{array}$ ahol $A$-t ugyanúgy definiáljuk, mint az előző esetben, $B$ értéke pedig $a_{2t+1}$, $a_{2t+2}$, vagy pedig e kettő összege aszerint, hogy $r=1$, $2$, vagy $3$, feltéve, hogy $s\ne t$. Ha $s=t$, akkor is könnyen látható, hogy $S$ értéke $a_{2s+1}+a_{2s+2}$, $a_{2s+2}$, vagy $a_{2s+1}$. Kivételt képezne az az egyetlen esetet, amikor $s=t$ és $q=r=2$. Ez azonban nem fordulhat elő, hiszen ekkor $S=a_{2s+2}-a_{2s+1}$ lenne, az $a_1$, $a_2$, $\text{...}$, $a_{2k}$ számok közül viszont semelyik kettő különbsége nem osztható $N$-nel.   III. megoldás. (Kovács Erika Renáta megoldása.) Ismét tegyük fel, hogy az $a_1$, $\text{...}$, $a_{2k}$ számok páronként különböző maradékot adnak $\left(n+k\right)$-val osztva. Vezessük be az $A=\left\{a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_{2k}\right\}$ jelölést, és legyen $b_1=a_1$. Ha valamilyen $1<j\le k+1$ esetén a $b_1$, $b_2$, $\text{...}$, $b_{j-1}$ számokat már definiáltuk, akkor legyen $b_j$ az $A$ halmaznak egy olyan eleme, amelyik a $b_1$, $b_2$, $\text{...}$, $b_{j-1}$, $b_1+b_2$, $b_1+b_2+b_3$, $\text{...}$, $b_1+b_2+\text{...}+b_{j-1}$ számok egyikével sem ad azonos maradékot $\left(n+k\right)$-val osztva. Ilyen szám valóban létezik, hiszen ezekkel a feltételekkel az $A$ halmaznak legfeljebb $\left(j-1\right)+\left(j-2\right)<2k$ elemét zártuk ki. Jelölje $b_{k+2}$, $b_{k+3}$, $\text{...}$, $b_{2k}$ az $A$ halmaz fennmaradó elemeit valamilyen sorrendben, és tekintsük a következő $n+k$ számot: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle s_i}& {\displaystyle =b_1+b_2+\text{...}+b_i}\hfill & \hfill {\displaystyle \left(1\le i\le 2k\right)\mathrm{,}}\\ \hfill {\displaystyle s_j}& {\displaystyle =a_1+a_2+\text{...}+a_j}\hfill & \hfill {\displaystyle \left(2k<i\le n\right)\mathrm{,}}\\ \hfill {\displaystyle s_{n+1}}& {\displaystyle =b_2\mathrm{,}{s}_{n+2}=b_3\mathrm{,}\text{...}\mathrm{,}{s}_{n+k}=b_{k+1}\mathrm{.}}\hfill \end{array}}}\end{array}$ Ha ezek közül valamelyik osztható $\left(n+k\right)$-val, akkor készen is vagyunk, ellenkező esetben viszont közülük kettő azonos maradékot ad $\left(n+k\right)$-val osztva, ezek különbsége tehát ismét csak osztható $\left(n+k\right)$-val. Az nyilván nem lehetséges hogy mindkét szám az utolsó $k$ darab közül kerüljön ki, hiszen ezek páronként különböző maradékkal rendelkeznek. Ha mindkét szám az első $n$ szám között van, akkor különbségük éppen az $a_i$ számok közül néhánynak az összege, ebben az esetben tehát megint csak célhoz értünk. Végül, ha a két szám közül az egyik $s_i$, ahol $1\le i\le n$, a másik pedig $s_{n+j}$, $1\le j\le k$, akkor a $b_i$ számok megválasztása miatt $i>j$ kell, hogy teljesüljön. Ekkor azonban $s_{n+j}=b_{j+1}$ éppen az $s_i$ egyik összeadandója, következésképpen az $\left(n+k\right)$-val osztható $s_i-s_{n+j}$ szám most is felírható az $a_i$ számok közül néhánynak az összegeként.   IV. megoldás. (Zábrádi Gergely ötlete.) Most egy indukciós bizonyítást mutatunk. Pontosabban az alábbi erősebb állítást fogjuk teljes indukcióval igazolni. Állítás. Legyenek $m$, $n$ pozitív egész számok. Ha az $a_1$, $a_2$, $\text{...}$, $a_n$ egész számok legalább $2i$ különböző maradékot adnak $m$-mel osztva, akkor vagy van közöttük néhány, amelyek összege osztható $m$-mel, vagy képezhető belőlük legalább $n+i$ olyan összeg, amelyek páronként különböző maradékot adnak $m$-mel osztva. Ebből az állításból $m=n+k$, $i=k$ választással az eredeti feladat megoldása azonnal leolvasható. Ha $i=0$, akkor egyszerűen tekintjük az $a_1$, $a_1+a_2$, $\text{...}$, $a_1+a_2+\text{...}+a_n$ összegeket; ha ezek között van két olyan, amelyik azonos maradékot ad $m$-mel osztva, akkor különbségük, ami szintén néhány $a_i$ összege, osztható $m$-mel. Tegyük fel most egy pillanatra, hogy $i=1$ esetén is igazoltuk már az állítást. Az indukciós lépéshez legyen $j\ge 1$ és tegyük fel azt is, hogy az állítás igazolást nyert már $i=j$ esetén is. Ebből $i=\left(j+1\right)$-re a következőképpen kaphatjuk meg az állítást. Legyenek $a_1$, $a_2$, $\text{...}$, $a_n$ olyan egész számok, amelyek legalább $2j+2$ különböző maradékot adnak $m$-mel osztva. Válasszunk ki közülük két különböző maradékot adót, és tekintsük az összes olyan $a_i$-t, amelyik ezek valamelyikével kongruens modulo $m$. Az általánosság megszorítása nélkül feltehetjük, hogy ezek éppen az $a_{t+1}$, $a_{t+2}$, $\text{...}$, $a_n$ számok. Az $a_1$, $a_2$, $\text{...}$, $a_t$ számokról tudjuk azt, hogy legalább $2j$ különböző maradékot adnak $m$-mel osztva. Tegyük fel, hogy az $a_i$ számokból nem képezhető $m$-mel osztható összeg. Ekkor az indukciós feltevés és az $i=1$ esetre vonatkozó feltevés értelmében az $a_1$, $a_2$, $\text{...}$, $a_t$ számokból képezhető $t+j$ különböző maradékot adó összeg, az $a_{t+1}$, $a_{t+2}$, $\text{...}$, $a_n$ számokból pedig képezhető $n-t+1$ különböző maradékot adó összeg. Jelölje ezeket rendre $s_1$, $s_2$, $\text{...}$, $s_{t+j}$, illetve $r_1$, $r_2$, $\text{...}$, $r_{n-t+1}$. Minden további nélkül feltehető az is, hogy $s_1=a_1+a_2+\text{...}+a_t$. Tekintsük most a következő $n+j+1$ számot: $s_1$, $s_2$, $\text{...}$, $s_{t+j}$, $s_1+r_1$, $s_1+r_2$, $\text{...}$, $s_1+r_{n-t+1}$, ezek bármelyike felírható az $a_i$ számok közül néhánynak az összegeként. Tudjuk, hogy az első $t+j$ szám páronként inkongruens modulo $m$, és hasonlóképpen az utolsó $n-t+1$ is az. Az sem lehet, hogy valamelyik $s_b$ ugyanolyan maradékot ad $m$-mel osztva, mint $s_1+r_c$, hiszen különbségük, $\left(s_1-s_b\right)+r_c$ jól láthatóan néhány $a_i$ összege. A felsorolt $n+j+1$ szám tehát páronként inkongruens modulo $m$, és éppen ezt akartuk megmutatni. Annyi van már csak hátra, hogy a fent kimondott állítást $i=1$ esetén is igazoljuk. Tegyük fel tehát, hogy az $a_1$, $a_2$, $\text{...}$, $a_n$ számok közül $a_1$ és $a_2$ különböző maradékot adnak $m$-mel osztva. Ha az $a_1\mathrm{,}{a}_2\mathrm{,}{a}_1+a_2\mathrm{,}{a}_1+a_2+a_3\mathrm{,}\text{...}\mathrm{,}{a}_1+a_2+\text{...}+a_n$ számok között van kettő, ami ugyanazt a maradékot adja, akkor különbségük, ami nem más, mint néhány $a_i$ összege, osztható lesz $m$-mel. Ellenkező esetben pedig máris találtunk $n+1$ olyan összeget, ami mind különböző maradékot ad $m$-mel osztva.   Megjegyzések. 1. Ahogy azt Gyenes Zoltán és Kiss Gergely is megjegyzik, az első megoldásból (és az azzal lényegében megegyező másodikból is) világosan látszik, hogy nem kell megkövetelnünk $2k$ különböző maradék létezését: elegendő, ha az $a_i$ számokból kiválasztható $k$ olyan pár, hogy az azonos párban lévő számok különböző maradékot adnak $\left(n+k\right)$-val osztva. Ez megtehető már akkor is (hogyan?), ha csak $k+1$ különböző maradék létezését követeljük meg (feltéve persze, hogy $2k\le n$). 2. A KöMaL 2000. decemberi számának A. 252. feladata szerint a $2k\le n$ feltételre valójában nincs is szükség: a feladatban megfogalmazott állítás igazolásához elég annyit feltenni, ahogy az $a_1$, $a_2$, $\text{...}$, $a_n$ számok legalább $k+1$ különböző maradékot adnak $\left(n+k\right)$-val osztva. Az alábbiakban erre mutatunk két különböző bizonyítást. 3. Megjegyezzük még, hogy Szemerédi Endre egy nehéz eredményére támaszkodva ez a feltétel is lényegesen gyengíthető: ha $k$ értéke $n$-hez képest ,,elég nagy'', akkor elegendő annyit feltenni, hogy az $a_i$ számok több, mint $c\sqrt[]{k}$ különböző maradékot adnak $\left(n+k\right)$-val osztva.   V. megoldás. (Csikvári Péter megoldásából.) Ha $k=0$, akkor a feltétel semmitmondó, és a bizonyítandó állítás következik a II. megoldás elején kimondott egyszerű állításból. A továbbiakban legyen tehát $k>0$. Tegyük fel, hogy az $a_1$, $a_2$, $\text{...}$, $a_{k+1}$ számok különböző maradékot adnak $\left(n+k\right)$-val osztva. Legyen $s=a_1+a_2+\text{...}+a_{k+1}$, és tekintsük $1\le i\le k+1$ esetén az $a_i$ és $b_i=s-a_i$ számokat, valamint $1\le j\le n-k$ esetén a $c_j=a_1+a_2+\text{...}+a_{k+j}$ számokat, ez összesen $n+k+2$ egész szám. Vizsgáljuk meg, hogyan adhat ezek közül kettő ugyanolyan maradékot $\left(n+k\right)$-val osztva. Az $a_i$ számok páronként különböző maradékot adnak, csakúgy mint a $b_i$ számok. Ha a $c_j$ számok közül kettő ugyanazt a maradékot adja, akkor már készen is vagyunk. Hasonlóképpen készen vagyunk akkor is, ha valamelyik $c_j$ szám ugyanolyan maradékot ad, mint valamelyik $a_i$ vagy $b_i$, hiszen mind maga az $a_i$ szám, mind pedig a $b_i$ minden egyes összeadandója szerepel bármelyik $c_j$ összeadandói között. Mivel $a_i$ a $b_j$-nek is összeadandója $j\ne i$ esetén, feltehetjük azt is, hogy ilyen esetekben $a_i$ és $b_j$ különböző maradékot adnak. Összefoglalva, feltehetjük tehát, hogy ha a fent felsorolt $n+k+2$ szám között kettő azonos maradékot ad $\left(n+k\right)$-val osztva, akkor ez a két szám $a_i$ és $b_i$ egy alkalmas $1\le i\le k+1$ indexre. Minden egyéb esetben ugyanis a bizonyítandó állítás az elmondottak miatt rögtön következik. Vegyük észre azt is, hogy azonnal befejezettnek tekinthetjük a bizonyítást akkor is, ha a felsorolt $n+k+2$ szám valamelyike osztható $\left(n+k\right)$-val. Egyetlen olyan eset képzelhető már csak el, amelyben még nem végeztük el a bizonyítást, nevezetesen ha 3 különböző $i$ index is létezik úgy, hogy $a_i$ és $b_i$ ugyanazt a maradékot adják, vagyis különbségük, $s-2a_i$ osztható $\left(n+k\right)$-val. Legyenek ezek $i_1$, $i_2$ és $i_3$, ekkor a $2a_{i_1}$, $2a_{i_2}$ és $2a_{i_3}$ számok ugyanolyan maradékot adnak $\left(n+k\right)$-val osztva. Nem nehéz megmutatni, hogy ez csak úgy lehetséges, ha az $a_{i_1}$, $a_{i_2}$, $a_{i_3}$ számok közül kettőnek a maradéka megegyezik, ellentétben a megoldás legelején tett feltevésünkkel. Ez mutatja, hogy a bizonyítást már minden esetben elvégeztük.   VI. megoldás. (Nagy Zoltán megoldásából.) Ha a számok közül valamelyik osztható $\left(n+k\right)$-val, akkor már készen is vagyunk, találtunk egy egytagú megfelelő összeget. Tegyük fel tehát, hogy az $a_i$ számok $p$ különböző maradékot ($p\ge k+1$) adnak $\left(n+k\right)$-val osztva, és ezek $0<m_1<m_2<\text{...}<m_p<n+k$. Ha egy összeg minden egyes tagját egy azzal azonos maradékot adó számmal helyettesítünk, a kapott összeg nyilván pontosan akkor lesz osztható $\left(n+k\right)$-val, ha az eredeti összeg is ilyen volt. Ezért feltehetjük azt is, hogy mindegyik $a_i$ valamelyik $m_j$-vel egyenlő. Állítsuk nagyság szerinti sorrendbe az $a_i$ számokat, vagyis legyen $a_1=a_2=\text{...}=a_{k_1}=m_1$, $a_{k_1+1}=a_{k_1+2}=\text{...}=a_{k_2}=m_2$, $\text{...}$, $a_{k_{p-1}+1}=\text{...}=a_n=m_p$, ahol $1\le k_1<k_2<\text{...}<k_{p-1}<n$. Tekintsük most minden $1\le i\le n$ esetén az $s_i=a_1+a_2+\text{...}+a_i$ összeget, és minden $1\le j\le p-1$ esetén a $t_j=a_1+a_2+\text{...}+a_{k_j-1}+a_{k_j+1}$ összeget is. Ez összesen $n+p-1\ge n+k$ szám. Ha ezek között van $\left(n+k\right)$-val osztható, akkor készen vagyunk. Ellenkező esetben kell, hogy legyen kettő, amelyik ugyanolyan maradékot ad $\left(n+k\right)$-val osztva. Ha az $s_i$ számok között van két ilyen, akkor a szokásos indoklás működik. Ha $s_i-t_j$ osztható $\left(n+k\right)$-val valamilyen $i$, $j$ esetén, akkor ismét csak készen vagyunk. Ha ugyanis $i<k_j$, akkor az $s_i$ összeg valódi része a $t_j$ összegnek, és ezért $t_j-s_i$ néhány $a_i$ összege. Ha $i>k_j$, akkor pedig a $t_j$ összeg képezi valódi részét az $s_i$ összegnek. Az pedig nem lehet, hogy $i=k_j$, mert ekkor $s_i-t_j=a_{k_j}-a_{k_j+1}=m_j-m_{j+1}$ lenne, ami nem osztható $\left(n+k\right)$-val. Végül tegyük fel, hogy $t_{\ell }-t_j$ osztható $\left(n+k\right)$-val valamilyen $1\le j<\ell \le p-1$ esetén. Ha még $j+1<\ell$ is teljesül, akkor könnyen látható, hogy $t_{\ell }-t_j$ az $a_i$ számok közül néhánynak az összege. Ugyanez a helyzet akkor is, ha $\ell =j+1$ és $k_{j+1}\ge k_j+2$. Az pedig nem lehetséges, hogy $\ell =j+1$ és $k_{j+1}=k_j+1$, ekkor ugyanis $t_{\ell }-t_j=a_{k_{j+1}+1}+a_{k_j}-a_{k_{j+1}}=m_{j+2}+m_j-m_{j+1}$. Viszont az $m_i$ számokra tett feltevés miatt nyilván $0<m_j<m_{j+2}+m_j-m_{j+1}<m_{j+2}<n+k$, vagyis az egyetlen megmaradt esetben $t_{\ell }-t_j$ nem osztható $\left(n+k\right)$-val.