Kezdőlap


Cím:	A zsák meg a foltjai
Szerző(k):	fordította: Paulin Elemér , I. M. Jaglom
Füzet:	2001/január, 10 - 20. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A Kvant című, orosz ifjúsági matematika‐fizika folyóiratban jelent meg a következő feladat:^{$^{*}$}A feladat kitűzője E. B. Denkin, sorszáma M. 185. A rövid megoldás megtalálható a Kvant 1973. évi 10. számában.
Egy egységnyi területű zsákon öt folt található, amelyek bármelyikének a területe legalább $\frac{1}{2}$ . Mutassuk meg, hogy van a foltok között kettő, melyek közös részének területe legalább $\frac{1}{5}$ .
A következőkben egyszerűbb feladatokon keresztül a probléma általánosításához is eljutunk. A felmerülő nehezebb feladatokat $*$ -gal jelöltük. Az alábbiakban a zsákot, valamint annak területét is (a feladatban ez egységnyi) $M$ betűvel jelöljük majd, a foltokat és azok területeit pedig $M_{1}$ , $M_{2}$ , $M_{3}$ , $M_{4}$ , $M_{5}$ -tel. Szükségünk lesz például az $M_{1}$ és $M_{2}$ foltok közös részére; ezt $M_{12}$ jelöli majd, és hasonlóan, az $M_{1}$ , $M_{2}$ , $M_{3}$ foltok közös részét $M_{123}$ stb. Reméljük, a szövegből világosan kiderül majd, mikor beszélünk egy alakzatról és mikor annak területéről.
Lássunk hozzá a feladat megoldásához!
Abból, hogy a foltok területének összege, $M_{1} + M_{2} + M_{3} + M_{4} + M_{5} \geq \frac{5}{2}$ , tehát nagyobb a zsák területénél (hiszen $M = 1$ ), következik, hogy a foltok között vannak átfedések. A feladatban alsó korlátot kell keresnünk a foltok páronkénti közös részének a területére, meg kell becsülnünk az $M_{12}$ , $M_{13}$ , $...$ , $M_{45}$ számok legnagyobbikát.
Először megmutatjuk, hogy

\begin{matrix} M - (M_{1} + M_{2} + M_{3} + M_{4} + M_{5}) + (M_{12} + M_{13} + M_{14} + ... + M_{45}) \geq 0. \end{matrix}

(1)

Ha a foltok között nem volnának átfedések, akkor már az

M - (M_{1} + M_{2} + M_{3} + M_{4} + M_{5})

különbség sem lenne negatív; ez a különbség egyenlő volna a zsák azon részének a területével, ahol egyáltalán nincsen folt. Mivel a foltok metszik egymást, az

M_{1} + M_{2} + M_{3} + M_{4} + M_{5}

összeg lényegesen nagyobb, mint a zsák foltokkal fedett részének

S

területe; itt természetesen

S \leq M = 1

. Valóban, az

M_{1} + M_{2} + M_{3} + M_{4} + M_{5}

összegben az

M_{12}

részt kétszer is számoltuk, mivel az

M_{1}

és az

M_{2}

tagok is tartalmazzák; ugyanígy, az

M_{123}

részt háromszor, és így tovább.
Most bebizonyítjuk, hogy

\begin{matrix} S \geq \sum_{}^{} M_{i} - \sum_{}^{} M_{i j}, \end{matrix}

(1')

ahol a képletben

\sum_{}^{} M_{i} = M_{1} + M_{2} + M_{3} + M_{4} + M_{5}

;

\sum_{}^{} M_{i j} = M_{12} + M_{13} + ... + M_{45}

, és a továbbiakban is eszerint használjuk a

\sum_{}^{}

jelölést. Mivel

M \geq S

, innen már következik az (1) egyenlőtlenség, annak alapján pedig már megbecsülhetjük a legalább kétszer lefedett területek

M_{12}

M_{13}

...

nagyságát. Valóban, (1)-ből következik, hogy

\begin{matrix} M_{12} + M_{13} + ... + M_{45} \geq (M_{1} + M_{2} + M_{3} + M_{4} + M_{5}) - M \geq \frac{5}{2} - 1 = \frac{3}{2} . \end{matrix}

A foltok páronkénti átfedéseinek száma

(\binom{5}{2}) = 10

, azért az

M_{12}

M_{13}

...

M_{45}

számok legnagyobbika nem kisebb, mint

\frac{3}{2} : 10 = \frac{3}{20}

. Becslésünk sajnos gyengébbnek bizonyult a szükségesnél, mivel

\frac{1}{5} > \frac{3}{20}

1. feladat. Az egységnyi területű zsákon kilenc, egyenként

\frac{1}{5}

területű folt található. Mutassuk meg, hogy van közöttük kettő, amelyek közös részének területe legalább

\frac{1}{45}

A szitaformula

A fentiekben a zsák foltozott részének

S

területére kapott

(1')

becslés nem bizonyult eléggé élesnek. Próbálkozzunk finomabb módszerrel: hagyjuk el

(1')

jobb oldaláról az olyan,

M_{i j}

alakú részek területeit, amelyeket egyszerre legalább három folt fed le. Eddig ugyanis

M_{123}

például megtalálható a pozitív előjellel szereplő

M_{1}

M_{2}

M_{3}

és a negatív előjellel szereplő

M_{12}

M_{13}

M_{23}

tagokban is, ezért az

M_{123}

terület egyáltalán nem szerepel

(1')

jobb oldalán. Így

S

pontosabb becslését adja a

\sum_{}^{} M_{i} - \sum_{}^{} M_{i j} + \sum_{}^{} M_{i j k}

összeg. Természetesen még ez sem pontos, itt ugyanis kétszer számoltuk a zsák azon részét, amit egyszerre legalább négy folt fed le; az

M_{1234}

mennyiséget például a páratlanszor fedő

M_{1}

M_{2}

M_{3}

M_{4}

M_{123}

M_{124}

M_{134}

M_{234}

tagokban összesen 8-szor pozitív, a párosszor fedő

M_{12}

M_{13}

M_{14}

M_{23}

M_{24}

és

M_{34}

tagokban pedig összesen 6-szor negatív előjellel vettük figyelembe.
A korábbinál jobban közelíti tehát

S

értékét a

\begin{matrix} \sum_{}^{} M_{i} - \sum_{}^{} M_{i j} + \sum_{}^{} M_{i j k} - \sum_{}^{} M_{i j k l} \end{matrix}

összeg; ez már ,,majdnem egyenlő"

S

pontos értékével. Itt már a zsák minden olyan részét figyelembe vettük, amelyet legfeljebb négy folt fed le. De a zsák ,,legkényesebb'', ötszörösen foltozott része kiesik a fenti összegből, mivel egyszerre van ott az

M_{1}

M_{2}

M_{3}

M_{4}

M_{5}

;

M_{123}

M_{124}

...

M_{345}

tagokban (ez 15 pozitív előjelű tag) és az

M_{12}

M_{13}

...

M_{45}

M_{1234}

M_{1235}

M_{1245}

M_{2345}

tagokban is (ez 15 negatív előjelű tag). Tehát

S

pontos értékét úgy kapjuk, ha az utolsó összeghez hozzáadjuk az

M_{12345}

tagot. Ekkor

\begin{matrix} S = \sum_{}^{} M_{i} - \sum_{}^{} M_{i j} + \sum_{}^{} M_{i j k} - \sum_{}^{} M_{i j k l} + M_{12345} \end{matrix}

(2)

(itt

i

j

k

l = 1

, 2, 3, 4 vagy 5).
Legyen

σ

a zsák ép részének a területe, amelyet egyetlen folt sem fed le. Mivel

σ = M - S

és természetesen

σ \geq 0

, így

\begin{matrix} σ = M - \sum_{}^{} M_{i} + \sum_{}^{} M_{i j} - \sum_{}^{} M_{i j k} + \sum_{}^{} M_{i j k l} - M_{12345} \geq 0. \end{matrix}

(3)

A (3) összefüggést az

M

zsák többszörösen foltozott részeinek szakaszos eltávolításával és azoknak a részeknek a visszaillesztésével kaptuk, amelyeket többször is eltávolítottunk; az összefüggést magyarul szitaformulának nevezik. A módszert és a formulát ‐ amelynek más alakja is ismeretes ‐ sok kombinatorikai feladatban használják. Érdemes átgondolni és felírni a képletet akkor is, ha a foltok száma

n

. Talán bonyolultnak tűnik, de csak a fenti egyszerű elv matematikai formája.

\begin{matrix} \begin{matrix} σ & = M - \sum_{}^{} M_{i_{1}} + \sum_{}^{} M_{i_{1} i_{2}} - \sum_{}^{} M_{i_{1} i_{2} i_{3}} + \sum_{}^{} M_{i_{1} i_{2} i_{3} i_{4}} - ... \\ ... + {(- 1)}^{n - 1} \sum_{}^{} M_{i_{1} i_{2} i_{3} ... i_{n - 1}} + {(- 1)}^{n} M_{123 ... n} \geq 0 & (4) \end{matrix} \end{matrix}

(itt az

i_{1}

i_{2}

...

i_{n = 1}

indexek az 1, 2, 3,

...

n

értékek bármelyikét fölvehetik, de az

M_{i_{1} i_{2} ... i_{k}}

rész

i_{1}

i_{2}

...

i_{n}

indexei feltétlenül különbözők).

Feladatok

2. Írjuk fel és bizonyítsuk be a szitaformulát, ha

n = 6

3*. Bizonyítsuk be a (4) formulát.

4. Egy táborban 220 gyerek nyaral. Hatféle sportra van lehetőség, ezek: atlétika (

a

), röplabda (

r

), kosárlabda (

k

), labdarúgás (

l

), birkózás (

b

) és sakk (

s

). Az egyes sportágakban résztvevő gyerekek száma rendre:

(a) - 30

(r) - 26

(k) - 32

(l) - 31

(b) - 28

(s) - 36

. Az említettek közül 53-an többféle sporttal is megpróbálkoztak: közülük 24-en három vagy annál is több, 9-en legalább négy és a 3 leglelkesebb legalább ötféle sportot is kipróbált. Az utóbb említett 3 között van 1 ,,csodabogár", aki mind a hat sportággal szerencsét próbált. Hány lusta gyerek nyaralt ebben a táborban, aki tehát egyetlen sportággal sem próbálkozott?

A kiinduló feladat megoldása

Láttuk, hogy az

M - \sum_{}^{} M_{i} + \sum_{}^{} M_{i j} \geq 0

egyenlőtlenség nem adja meg kellő pontossággal a minket érdeklő

{max}_{}^{} M_{i j}

mennyiség értékét (így jelöljük az

M_{i j}

mennyiségek legnagyobbikát). Szükségképpen a teljes becslést használjuk majd, amely tehát a következő:

\begin{matrix} M - \sum_{}^{} M_{i} + \sum_{}^{} M_{i j} - \sum_{}^{} M_{i j k} + \sum_{}^{} M_{i j k l} - \sum_{}^{} M_{12345} \geq 0 \end{matrix}

(3')

A másik ötlet, hogy a (4) formula, mint általános összefüggés, valamennyi szóbajövő halmazra alkalmazható, így például ha

M_{i}

-re írjuk fel, akkor azt kapjuk, hogy

\begin{matrix} σ_{1} = M_{1} - \sum_{}^{} M_{1 i} + \sum_{}^{} M_{1 i j} - \sum_{}^{} M_{1 i j k} + M_{12345} \geq 0, \end{matrix}

ahol

σ_{1}

M_{1}

foltnak az a része, amelyet más folt nem fed le. Az

i

j

k

indexek a 2, 3, 4, 5 számok összes lehetséges értékét felveszik. Hasonló egyenlőtlenségeket írhatunk fel az

M_{2}

M_{3}

M_{4}

M_{5}

foltokra is:

\begin{matrix} \begin{matrix} σ_{2} & = M_{2} - \sum M_{2 i} + \sum M_{2 i j} - \sum M_{2 i j k} + M_{12345} \geq 0, \\ ⋮ \\ σ_{5} & = M_{5} - \sum M_{5 i} + \sum M_{5 i j} - \sum M_{5 i j k} + M_{12345} \geq 0. \end{matrix} \end{matrix}

Ha összeadjuk az így kapott öt egyenlőtlenséget, akkor a

\begin{matrix} \sum M_{i} - 2 \sum M_{i j} + 3 \sum M_{i j k} - 4 \sum M_{i j k l} + 5 M_{12345} \geq 0. \end{matrix}

(5)

egyenlőtlenséget kapjuk. (Ellenőrizzük az együtthatókat!)
Próbáljuk most elkészíteni a

(3')

és az (5) egyenlőtlenségek olyan kombinációját, amelyben nem szerepelnek a

\sum M_{i j k}

típusú összegek, tehát a zavaróan ,,nagy'', hármasan fedett részek. Látható, hogy ehhez (5)-öt

\frac{1}{3}

-dal kell szorozni, és ezt kell hozzáadni

(3')

-höz. Így a következő egyenlőtlenséget nyerjük:

\begin{matrix} M - \frac{2}{3} \sum M_{i} + \frac{1}{3} \sum M_{i j} - \frac{1}{3} \sum M_{i j k l} + \frac{2}{3} M_{12345} \geq 0. \end{matrix}

(6)

Megmutatjuk, hogy ebből

\begin{matrix} M - \frac{2}{3} \sum M_{i} + \frac{1}{3} \sum M_{i j} \geq 0 \end{matrix}

(7)

következik.
Valóban, hiszen

M_{12345}

része az

M_{i j k l}

halmazok mindegyikének, azért

\sum M_{i j k l} \geq 5 M_{12345}

, és így még inkább

- \frac{1}{3} \sum M_{i j k l} + \frac{2}{3} M_{12345} \leq 0

. A (7) egyenlőtlenséget átrendezve kapjuk, hogy

\begin{matrix} \sum M_{i j} \geq 2 \sum M_{i} - 3 M \geq 2 \cdot (5 \cdot \frac{1}{2}) - 3 = 2. \end{matrix}

Mivel az

M_{i j}

,,dupla lefedettségek'' száma 10, ezért közülük legalább egynek az értéke nem kisebb, mint

2 : 10 = \frac{1}{5}

, és éppen ezt kellett bizonyítani! A felhasznált egyenlőtlenségek láncolatát végignézve látható, hogy a fenti becslésben lehetséges egyenlőség, mégpedig pontosan akkor, ha

S = M

, vagyis ha a foltok a zsák teljes területét lefedik, továbbá, ha minden

M_{i} = \frac{1}{2}

, minden

M_{i j} = \frac{1}{5}

, és minden

M_{i j k l} = 0

. Eredményünk éles:

\begin{matrix} 12 & 13 & 14 & 15 & 23 \\ 24 & 25 & 34 & 35 & 45 \\ 123 & 124 & 125 & 134 & 135 \\ 145 & 234 & 235 & 245 & 345 \end{matrix}

Az 1. ábrán látható elrendezésben az

M

területű (nagy) téglalap játssza a zsák szerepét, az egyes négyzeteken szereplő számok pedig azt mutatják, hogy hányas számú folt vesz részt a szóban forgó terület lefedésében. Talán zavaró lehet, hogy a ,,foltok'' most nem összefüggő darabok, de a feladatban csak a területük fontos, alakjuk és szerkezetük nem.
Fogalmazzuk most meg az általánosabb feladatot, amelynek a most megoldott csak speciális esete.

A kétszeresen foltozott terület általában

Az egységnyi területű

M

zsákon

n

folt található, ezek

M_{1}

M_{2}

...

M_{n}

; egyikük területe sem kisebb egy adott pozitív

α

számnál. Becsüljük meg az

M_{i j}

számok legnagyobbikának területét. Más szavakkal: minden

n

-szeresen foltozott zsákon megkeressük a kétszeresen fedett

M_{i j}

területek legnagyobbikát, és azt kérdezzük, hogy mennyi az így talált maximumok legkisebb értéke. Feltételezzük, hogy ez a minimum létezik, bár végtelen számhalmazról lévén szó ez egyáltalán nem nyilvánvaló. Ilyen jellegű ,,minimax'' feladatok megoldása, amikor maximumként értelmezett számok minimumát keressük, nagyon fontos a modern matematikában. A keresett

{min}_{}^{} {max}_{}^{} M_{i j}

természetesen függ az adott

α

számtól, annak függvénye; mivel a foltok számától, az

n

-től is függ, ezért jelöljük

f_{n} (α)

-val. (Itt természetesen

0 \leq α \leq 1

és

n \geq 2

). A kiinduló ,,zsák‐folt'' feladatot megoldva az

f_{5} (\frac{1}{2}) = \frac{1}{5}

egyenlőséget bizonyítottuk be. A feladat általánosításában az

f_{n} (α)

függvényt kellene megadni

α

és

n

segítségével.
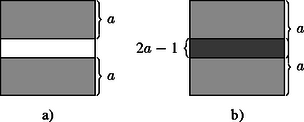
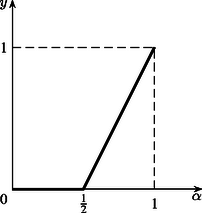
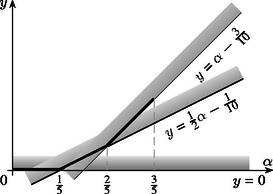
Tapasztalatok gyűjtése érdekében vizsgáljuk először az egyszerűnek tűnő

n = 2

esetet. Legyen tehát az egységnyi területű

M

zsákon két folt (

M_{1}

és

M_{2}

) úgy, hogy mindkettejük területe legalább

α

; feladatunk, hogy megtaláljuk az

M_{1}

és

M_{2}

foltok

M_{12}

közös részének a legkisebb

f_{2} (α)

területét. Világos, hogy ha

α \leq \frac{1}{2}

, akkor lehetséges, hogy egyáltalán nincsen átfedés (2.a ábra); ha pedig

α \geq \frac{1}{2}

, akkor kétszeresen fedett

M_{12}

terület legkisebb értéke

2 α - 1

(2.b ábra). Így

\begin{matrix} f_{2} (α) = {\begin{matrix} 0, & ha0 \leq α \leq \frac{1}{2}, \\ 2 α - 1, & ha\frac{1}{2} \leq α \leq 1, \end{matrix} \end{matrix}

(8)

a függvény grafikonja látható a 3. ábrán.

Feladat

5. Jellemezzük az

y = f_{3} (α)

függvényt.
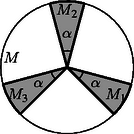
Útmutatás: vizsgáljuk az

M

körlap olyan egybevágó

M_{1}

M_{2}

M_{3}

körcikkeit, amelyek szimmetriatengelyei páronként

120^{\circ}

-os szöget zárnak be, középponti szögük mérőszáma pedig

α

, pontosabban a teljesszög

α

-szorosa. Kezdjük kicsi értékekkel (4. ábra), majd fokozatosan növeljük

α

értékét egészen 1-ig.

Öt folt

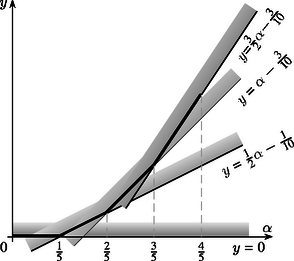
Térjünk most vissza az eredeti feladathoz, keressük, hogy legalább mekkora a kétszeresen lefedett terület, amennyiben az

M

zsákon található

M_{1}

M_{2}

M_{3}

M_{4}

M_{5}

foltok bármelyikének területe legalább

α

. Világos, hogy

f_{5} (α) \geq 0

, vagyis az

y = f_{5} (α)

függvény grafikonja nem helyezkedhet el az

x

tengely alatt (5. ábra). A függvény értéke lehet nulla, ha a foltok elrendezhetők úgy, hogy mindegyik

M_{i j}

értéke nulla. Ez pontosan akkor lehetséges, ha a foltok területének összege, amely a feltételek szerint legalább

5 α

, nem nagyobb 1-nél (mivel a zsák területe egységnyi):

f_{5} (α) = 0

, ha

0 \leq α \leq \frac{1}{5}

. Továbbá az (1) egyenlőtlenségből következik, hogy

\sum M_{i j} \geq \sum M_{i} - M \geq 5 α - 1

. Figyelembe véve, hogy a foltok ,,páronkénti (dupla) átfedéseinek'' száma egyenlő 10-zel, kapjuk, hogy

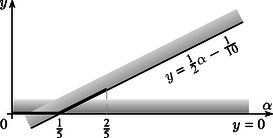
\begin{matrix} f_{5} (α) \geq \frac{1}{10} (5 α - 1) = \frac{1}{2} α - \frac{1}{10} . \end{matrix}

(9)

A (9) egyenlőtlenség minden szóba jövő

α

-ra igaz; így az

y = f_{5} (α)

függvény grafikonja nem helyezkedhet el az

y = \frac{1}{2} α - \frac{1}{10}

egyenes alatt (6. ábra). Ahhoz, hogy a (9)-ben éppen egyenlőség álljon, szükséges, hogy

\frac{1}{2} α - \frac{1}{10}

nagyobb legyen nullánál; ezen kívül még az is, hogy az (1) egyenlőtlenségben is az egyenlőség teljesüljön ‐ tehát mindegyik

M_{i j k}

értéke nulla kell, hogy legyen, és minden

M_{i j}

értéke ugyanannyi,

\frac{1}{2} α - \frac{1}{10}

kell legyen. De ha az összes

M_{i j k} = 0

, akkor mindegyik

α

területű folton, például az

M_{1}

-en, az egyenként

\frac{1}{2} α - \frac{1}{10}

területű

M_{12}

M_{13}

M_{14}

és

M_{15}

foltoknak már átfedések nélkül kell elhelyezkedniük. Ez csak akkor lehetséges, ha

4 (\frac{1}{2} α - \frac{1}{10}) \leq α

, azaz

α \leq \frac{2}{5}

. Sikerült tehát az

f_{5} (α)

függvényt kiterjesztenünk:

f_{5} (α) = \frac{1}{2} α - \frac{1}{10}

, ha

\frac{1}{5} \leq α \leq \frac{2}{5}

.
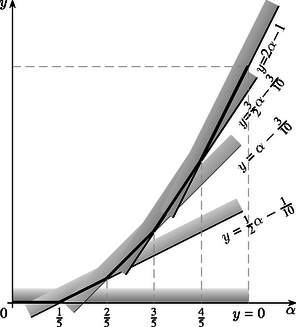
A továbbiakban ismét a (7) egyenlőtlenséget használjuk. Ebből az egyenlőtlenségből következik, hogy

\sum M_{i j} \geq 2 \sum M_{i} - 3 M \geq 2 (5 α) - 3 = 10 α - 3

, tehát

\begin{matrix} f_{5} (α) \geq \frac{1}{10} (10 α - 3) = α - \frac{3}{10} . \end{matrix}

(10)

A (10) egyenlőtlenség minden

α

esetén teljesül, vagyis az

f_{5} (α)

függvény grafikonja teljes egészében az

y = α - \frac{3}{10}

egyenes felett helyezkedik el (7. ábra); megjegyzendő, hogy (10)-ben csak akkor lehetséges egyenlőség, ha

\frac{2}{5} \leq α \leq \frac{3}{5}

(lásd a 6.a feladatot). A továbbiakban a szitaformulát nem csak a foltok

M_{i}

területére alkalmazzuk majd, mint a megoldásban tettük, hanem a kétszeresen és a háromszorosan fedett

M_{i j}

M_{i j k}

területekre is. Így, ha például az említett képletet az

M_{12}

területre használjuk, amelyen az

M_{123}

M_{124}

és

M_{125}

foltok helyezkednek el, a következőt kapjuk:

\begin{matrix} σ_{12} = M_{12} - \sum M_{12 i} + \sum M_{12 i j} - M_{12345} \geq 0. \end{matrix}

Összesen tíz ilyen egyenlőtlenség írható fel; ezeket összeadva kapjuk, hogy

\begin{matrix} \sum M_{i j} - 3 \sum M_{i j k} + 6 \sum M_{i j k l} - 10 M_{12345} \geq 0. \end{matrix}

(11)

Hasonlóan, az

M_{123}

-ra (ezen az

M_{1234}

és

M_{1235}

foltok találhatók) felírt szitaformula azt adja, hogy

\begin{matrix} σ_{123} = M_{123} - \sum M_{123 i} + M_{12345} \geq 0. \end{matrix}

Mivel a foltok

M_{i j k}

hármas átfedéseinek a száma 10, azért ha összeadjuk a megfelelő tíz egyenlőtlenséget, akkor kapjuk, hogy:

\begin{matrix} \sum M_{i j k} - 4 \sum M_{i j k l} + 10 M_{12345} \geq 0. \end{matrix}

(12)

Mostanra rendelkezésünkre állnak a

(3')

, (5), (11) és (12) egyenlőtlenségek, amelyek kapcsolatot teremtenek az

M

\sum M_{i}

\sum M_{i j}

\sum M_{i j k}

\sum M_{i j k l}

és

M_{12345}

mennyiségek között. Most tekintsük az (5) egyenlőtlenség

\frac{1}{2}

-szeresének, a (11)

\frac{1}{6}

-szorosának és a

(3')

egyenlőtlenségnek az összegét:

\begin{matrix} M - \frac{1}{2} \sum M_{i} + \frac{1}{6} \sum M_{i j} - \frac{1}{6} M_{12345} \geq 0 \end{matrix}

(13)

Az együtthatók megválasztása miatt ez már nem tartalmazza a háromszoros és a négyszeres

\sum M_{i j k}

, valamint a

\sum M_{i j k l}

tagokat. Elhagyva az ötszörösen fedett negatív tagot innen következik, hogy

\begin{matrix} M - \frac{1}{2} \sum M_{i} + \frac{1}{6} \sum M_{i j} \geq 0 \end{matrix}

és ezért

\begin{matrix} \begin{matrix} \sum M_{i j} \geq 3 \sum M_{i} - 6 M \geq 3 (5 α) - 6, \\ tehát \\ f_{5} (α) \geq \frac{1}{10} (15 α - 6) = \frac{3}{2} α - \frac{3}{5} . \end{matrix} \end{matrix}

Eszerint az

f_{5} (α)

függvény grafikonja nem helyezkedhet el az

y = \frac{3}{2} α - \frac{3}{5}

egyenes alatt (8. ábra). Készítsük most el a

(3')

, (5), (11), (12) egyenlőtlenségek

\begin{matrix} (3') + \frac{3}{5} \cdot (5) + \frac{3}{10} \cdot (11) + \frac{1}{10} \cdot (12) \end{matrix}

lineáris kombinációját; kapjuk, hogy

\begin{matrix} M - \frac{2}{5} \sum M_{i} + \frac{1}{10} \sum M_{i j} \geq 0. \end{matrix}

(15)

Itt már csak az

M

\sum M_{i}

és

\sum M_{i j}

tagok szerepelnek. A (15)-ből következik, hogy

\begin{matrix} \begin{matrix} \sum M_{i j} & \geq 4 \sum M_{i} - 10 M \geq \\ \geq 4 (5 α) - 10 = 20 α - 10, \end{matrix} \end{matrix}

tehát

\begin{matrix} f_{5} (α) \geq \frac{1}{10} (20 α - 10) = 2 α - 1. \end{matrix}

f_{5} (α)

függvény grafikonja tehát nem haladhat az

y = 2 α - 1

egyenes alatt, végeredményben tehát nem helyezkedhet el az 9. ábrán látható töröttvonal alatt; könnyen belátható, hogy a függvény grafikonja éppen azonos ezzel a töröttvonallal.

Feladatok

6. Bizonyítsuk be, hogy

a)

f_{5} (α) = α - \frac{3}{10}

, ha

\frac{2}{5} \leq α \leq \frac{3}{5}

; b)

f_{5} (α) = \frac{3}{2} α - \frac{3}{5}

, ha

\frac{3}{5} \leq α \leq \frac{4}{5}

;
c)

f_{5} (α) = 2 α - 1

, ha

\frac{4}{5} \leq α \leq 1

7. Jellemezzük az a)

f_{4} (α)

f_{6} (α)

függvényt.

A feladat általánosítása

Ezt az esetet az

n = 5

esethez hasonlóan tárgyaljuk. Világos, hogy

n

folt esetén az

M_{1}

M_{2}

...

M_{n}

foltok (ezek bármelyikének területe legalább

α

) akkor nem fedik egymást, ha az összterületük

\sum M_{i} \geq n α

, és ez az összterület nem nagyobb

M = 1

-nél (hiszen a zsák területe egységnyi). Ezért

f_{n} (α) = 0

, ha

0 \leq α \leq \frac{1}{n}

. A továbbiakban ismét a (4) egyenlőtlenségből (a szitaformulából) indulunk ki. Ebből most

\begin{matrix} M - \sum M_{i} + M_{i j} \geq 0 \end{matrix}

(16)

következik. (Miért?) Így

\begin{matrix} \sum M_{i j} \geq \sum M_{i} - M \geq n α - 1. \end{matrix}

Mivel az

M_{i j}

átfedések száma általában

(\binom{n}{2}) = \frac{n (n - 1)}{2}

, azért

\begin{matrix} f_{n} (α) \geq \frac{1}{n (n - 1) / 2} \cdot (n α - 1) = \frac{2}{n - 1} α - \frac{2}{n (n - 1)} . \end{matrix}

(17)

A (17) egyenlőtlenség csakis akkor válik egyenlőséggé, ha egyenlőséggé alakul a (16), vagyis ha (4)-ben az összes olyan tag, amelyik a

\sum M_{i j}

tag után következik, nulla. Szükséges ezen kívül még az is, hogy az egyenként

α

területű

M_{i}

foltok teljesen lefedjék az

M

zsákot. De ez esetben az

M_{1}

kétszeres lefedései, tehát az

M_{12}

M_{13}

...

M_{1 n}

(ezekből

n - 1

db van) az

M_{1}

foltot további átfedések nélkül fedik le mivel az összes

M_{i j k} = 0

. Miután ekkor

M_{1 i} = \frac{2}{n - 1} α - \frac{2}{n (n - 1)}

, azért

\begin{matrix} (n - 1) [\frac{2}{n - 1} α - \frac{2}{n (n - 1)}] \leq α, \end{matrix}

tehát

α \leq \frac{2}{n}

(és természetesen

α \leq \frac{1}{n}

).
A továbbiakban a már megszokott módon az

M_{i}

foltokra alkalmazzuk a szitaformulát, majd azok

M_{i j}

M_{i j k}

stb. átfedéseire. Alkalmazzuk ezt a képletet, például az

M_{1}

foltra, amelyet az

M_{12}

M_{13}

...

M_{1 n}

,,másodrendű foltok'' fednek:

\begin{matrix} \begin{matrix} M_{1} - \sum M_{1 i_{1}} + \sum M_{1 i_{1} i_{2}} - \sum M_{1 i_{1} i_{2} i_{3}} + ... \\ ... + {(- 1)}^{n - 2} \sum M_{1 i_{1} i_{2} ... i_{n - 2}} + {(- 1)}^{n - 1} M_{123 ... n} \geq 0 \end{matrix} \end{matrix}

(ahol

i_{1}

i_{2}

...

i_{n - 2} = 2

, 3,

...

n

). Ha összeadjuk az

M_{1}

M_{2}

...

M_{n}

foltokra felírt

n

db egyenlőtlenséget, akkor a következőt kapjuk:

\begin{matrix} \begin{matrix} \sum M_{i} - 2 \sum M_{i_{1} i_{2}} + 3 \sum M_{i_{1} i_{2} i_{3}} - ... \\ ... + {(- 1)}^{n - 2} \cdot (n - 1) \sum M_{i_{1} i_{2} ... i_{n - 1}} + {(- 1)}^{n - 1} \cdot n M_{123 ... n} \geq 0 & (18) \end{matrix} \end{matrix}

(hasonlítsuk össze az (5) egyenlőtlenséggel).
A (4)-ból és a (18)-ból a szokott módon iktathatók ki a

\sum M_{i_{1} i_{2} i_{3}}

tagok ‐ ehhez (18)

\frac{1}{3}

-szorosát kell hozzáadni a (4)-hez:

\begin{matrix} M - \frac{2}{3} \sum M_{i_{1}} + \frac{1}{3} \sum M_{i_{1} i_{2}} - \frac{1}{3} \sum M_{i_{1} i_{2} i_{3}} + ... + {(- 1)}^{n - 1} \frac{n - 3}{3} \cdot M_{123 ... n} \geq 0. \end{matrix}

(19)

A (19)-ből következik

\begin{matrix} M - \frac{2}{3} \sum M_{i_{1}} + \frac{1}{3} \sum M_{i_{1} i_{2}} \geq 0, \end{matrix}

(19a)

és így

\begin{matrix} \sum M_{i_{1} i_{2}} \geq 2 \sum M_{i_{1}} - 3 M \geq 2 (n α) - 3 = 2 n α - 3. \end{matrix}

Tehát

\begin{matrix} f_{n} (α) \geq \frac{1}{\frac{n (n - 1)}{2}} (2 n α - 3) = \frac{4}{n - 1} α - \frac{6}{n (n - 1)}, \end{matrix}

(20)

ahol egyenlőség csakis

\frac{2}{n} \leq α \leq \frac{3}{n}

esetén lehetséges (lásd a 8. feladatot). A fentiekhez hasonlóan folytatva a következő általános képlethez jutunk:

\begin{matrix} f_{n} (α) = 2 \frac{r - 1}{n - 1} α - \frac{r (r - 1)}{n (n - 1)}, \end{matrix}

(21)

\frac{r - 1}{n} \leq α \leq \frac{r}{n}

, ahol

r = 1

, 2, 3

...

n

Feladatok

8. Mutassuk meg, hogy (20)-ban csak akkor állhat egyenlőség, ha

\frac{2}{n} \leq α \leq \frac{3}{n}

9*. Mutassuk meg, hogy

f_{n} (α) = \frac{6}{n - 1} - \frac{12}{n (n - 1)}

, ha

\frac{3}{n} \leq α \leq \frac{4}{n}

10*. Bizonyítsuk be a (21) összefüggést.

I. M. Jaglom
fordította: Paulin Elemér

Ennek a cikknek a nyomán tűztük ki a B. 3378. feladatot, amelynek megoldása a 30. oldalon olvasható. A szerk.

^{$^{*}$}

^{1}