Kezdőlap


Cím:	Harmadrendű görbék II. Poncelet tétele
Szerző(k):	Hraskó András
Füzet:	2000/május, 264 - 275. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mint ismeretes, sárkányok nincsenek. Ez a primitív megállapítás talán kielégíti az egyszerű elmét, de nem a tudományt

...

Elég az hozzá, hogy a zseniális Cerebron, egzakt módszerekkel boncolgatva a problémát, a sárkányok három faját fedezte fel: a nullás, az imaginárius és a negatív sárkányokat. Mindezek, amint már említettük, nem léteznek, de mindegyik fajta egészen másképpen nem létezik. ¹
Stanisław Lem: Kiberiáda
(Harmadik utazás avagy a valószínűségi sárkányok)

A fogoly

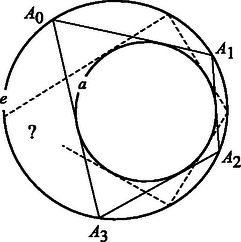
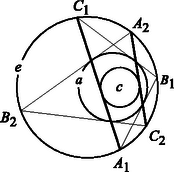
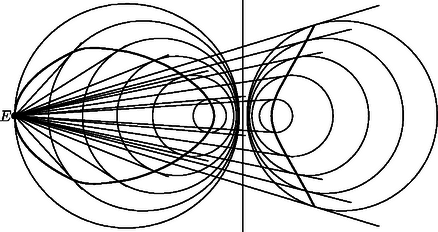
J. V. Poncelet Napóleon katonájaként 24 éves korában Moszkvából visszavonulóban Kutuzov seregének fogságába esett. 1812‐13 rettenetes hideg telén 800 km-t meneteltették őt és társait az orosz sztyeppén át a Volga partjáig, a szaratovi fogolytáborig. A rabságban Poncelet felelevenítette magában a bevonulás előtt nem sokkal befejezett egyetemi tanulmányait, olvasmányait. Mindezek új életre keltek benne. Könyvtártól elzártan, szellemi társakat nélkülözve, fizikai fájdalmaktól gyötörten a fiatal hadmérnök a geometria addig ismeretlen területeit fedezte fel. Megalkotta többek között az ideális pont fogalmát, megálmodott egy különleges leképezést, a polaritást², és elméjében furcsa körtáncra indultak a poligonok, itt született meg cikkünk témája, Poncelet tétele is.
Az életben maradt rabokat, köztük Poncelet-t, 1814 szeptemberében engedték szabadon. A mérnök-matematikus fogságban fogant gondolatai 1822-ben jelentek meg nyomtatásban az ,,Értekezés az alakzatok projektív tulajdonságairól" című könyvében. Ebben található az alábbi tétel:

Poncelet tétele: Legyenek adva az egymást nem érintő

e

és

a

körök,

a

e

belsejében. Az

e

körön tetszőlegesen választott

A_{0}

pontból indulva megszerkeszthetjük az

e

kör

A_{1}

A_{2}, ...

pontjait úgy, hogy az

A_{0} A_{1}

A_{1} A_{2}, ...

egyenesek érintsék az

a

kört és bármely két, a sorban egymást követő egyenes különbözzék egymástól.
Előfordulhat, hogy bizonyos számú lépésben visszajutunk a kezdőpontba, azaz

A_{n} = A_{0} .

Ebben az esetben az

e

kör bármely másik pontjából indulunk is ki, biztosan visszaérünk a kezdőpontba, mégpedig pontosan ugyanannyi lépésben (

n

), mint előzőleg.(1. ábra).

A tétel tehát nem azt mondja ki, hogy mindig van visszatérés, hanem azt, hogy a visszatérés kérdése, és a lépésszám nem a kezdőpont megválasztásától, hanem kizárólag a két kör nagyságától, egymához viszonyított elhelyezkedésétől függ.
A tétel állítása triviálisan teljesül koncentrikus körök esetén. Minden más esetben viszont meglehetősen nehéz a bizonyítás. Ez az első ránézésre talán ártatlannak tűnő tétel nemcsak születésének regényes körülményei miatt érdekes, de a XIX. századi matematika sűrűjébe vezető tartalma miatt is. Poncelet állítása, a két fejezettel később közölt általánosabb alakjában, ekvivalens a harmadrendű görbe csoporttulajdonságával és a trigonometrikus függvények általánosításainak, az elliptikus függvényeknek az addíciós tételeivel.
Poncelet körök helyett tetszőleges irreducibilis másodrendű görbékre mondta ki a tételt (lásd a 6. feladatot). Azt sem kellene megkövetelni, hogy az egyik görbe a másik belsejében legyen, de ez a fajta általánosítás nagyon megnehezítené az elemi tárgyalást.

Körsorok

O_{a} (u_{a}, v_{a})

középpontú

r_{a}

sugarú

a

kör (affin) egyenlete:

\begin{matrix} {(x - u_{a})}^{2} + {(y - v_{a})}^{2} - r_{a}^{2} = 0. \end{matrix}

(1)

Jelöljük az (1) egyenlet bal oldalán álló polinomot, mint

x

és

y

függvényét

a (x, y)

-nal. Ha a

P (ξ, η)

pont illeszkedik erre a körre, akkor

\begin{matrix} \begin{matrix} a (ξ, η) = 0, \\ ha viszont nem, akkor \\ a (ξ, η) \neq 0. \end{matrix} \end{matrix}

Az utóbbi esetben

a (ξ, η)

értéke nem csak azt árulja el, hogy a

P

pont nincs rajta a körön, hanem arról is ad információt, hogy hogyan nincs rajta.
A

a (ξ, η)

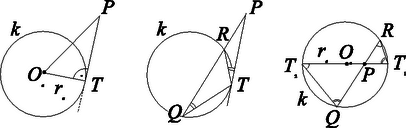
kifejezés fő része,

{(ξ - u_{a})}^{2} + {(η - v_{a})}^{2}

O_{a} P

szakasz hosszának négyzetét adja meg. Ha

a (ξ, η)

értéke negatív, az azt jelenti, hogy

O_{a} P^{2} < r_{a}^{2}

, azaz

P

a

kör belsejében helyezkedik el. Ha a vizsgált érték pozitív, akkor

P

a körön kívül van, ráadásul

a (ξ, η)

épp a

P

-ből a körhöz húzott érintő hosszának négyzete (2. ábra).
Ennél még némileg többet is mondhatunk. Mind a pozitív, mind a negatív esetben igaz, hogy a

P

-n át a körhöz húzott tetszőleges szelőnek a körrel vett

R

Q

metszéspontjaira a

P R \cdot P Q

érték állandó, azaz független a szelő választásától. Ez a kerületi és az érintőszárú kerületi szögek tételének felhasználásával és hasonló háromszögek segítségével igazolható.
Ezt az állandó értéket a

P

pont

k

körre vonatkozó hatványának is mondják és éppen egyenlő

O_{a} P^{2} - r_{a}^{2}

-tel, tehát

a (ξ, η)

értékével. ³
Ennek alapján azt mondhatjuk, hogy az

\begin{matrix} a (x, y) = t \end{matrix}

egyenletet azok a pontok elégítik ki, amelyeknek az

a

körre vonatkozó hatványa

t

;

t > 0

esetén tehát azok a pontok, amelyekből a

a

-hoz húzott érintő szakasz hosszának négyzete

t

.
Legyen adva az

a

körtől különböző

b

kör is, melynek egyenlete

\begin{matrix} b (x, y) = {(x - u_{b})}^{2} + {(y - v_{b})}^{2} - r_{b}^{2} = 0. \end{matrix}

Kereshetjük azokat a pontokat, melyekből az

a

-hoz, illetve a

b

-hez húzott érintő szakasz hosszának aránya egy adott érték. Általánosabban, legyen

c

azon pontok mértani helye a síkban, melyeknek az

a

-körre vonatkozó hatványa úgy aránylik a

b

körre vonatkozó hatványához, mint

α

β

-hoz. A

c

halmaz egyenlete:

\begin{matrix} β a (x, y) - α b (x, y) = 0. \end{matrix}

(2)

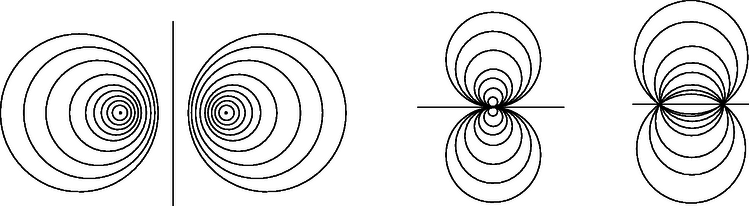
Ez is egy kör (esetleg pont, vagy üres halmaz, illetve

α = β

esetén egyenes) egyenlete, hiszen olyan kétváltozós másodfokú egyenlet, amelyben

x^{2}

és

y^{2}

együtthatója egyenlő (

α = β

esetén

0

)

x y

-os tag pedig nincsen benne.
A (2) alakú görbék halmazát az

a

és

b

generálta körsornak nevezzük. A körsor bármelyik két eleméből megkapható az összes többi elem, egyenleteik (2) alakú lineáris kombinációik segítségével. Tehát a körsort bármelyik két tagja generálja, azaz meghatározza.
Ha

a

és

b

egy körsor tetszőleges két köre,

c

pedig a körsor bármelyik eleme, akkor

c

különböző pontjainak az

a

-ra és

b

-re vonatkozó hatványainak aránya ugyanaz az érték.
Nem nehéz igazolni, hogy 3 fajta körsor van: nem metsző, érintő és metsző. Az elsőben semelyik két körnek sincs közös pontja, a másodikban a körök egy bizonyos pontban érintkeznek egymással, a harmadikban két közös ponton mennek át. (3. ábra.Lásd még az 1., 2. feladatokat.)

Poncelet gondolatmenete

Ebben a fejezetben keveset bizonyítunk, inkább csak vázoljuk Poncelet gondolatmenetét. Annál is inkább, mert az utolsó részben közölt bizonyítás az itteni részletekre is rávilágít.
L. Euler egy nevezetes tétele kapcsolatot teremt a háromszög beírt és körülírt körének

r

R

sugarai és középpontjaik

d

távolsága között:

\begin{matrix} R^{2} - d^{2} = 2 R r . \end{matrix}

(3)

A tétel bizonyítása megtalálható H.S.M. Coxeter és S. L. Greitzer: Az újra felfedezett geometria című könyvében (Gondolat Kiadó, 1977.) (2.1.2 Tétel), de a 3. feladat is segítséget ad a bizonyításhoz.
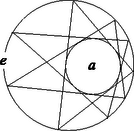
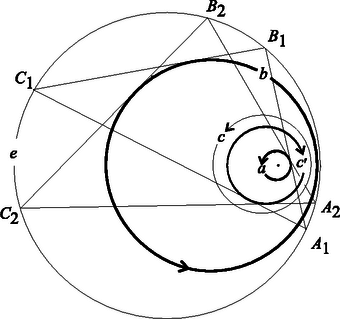
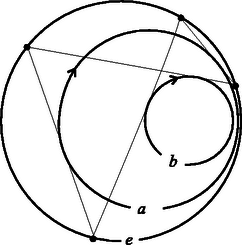
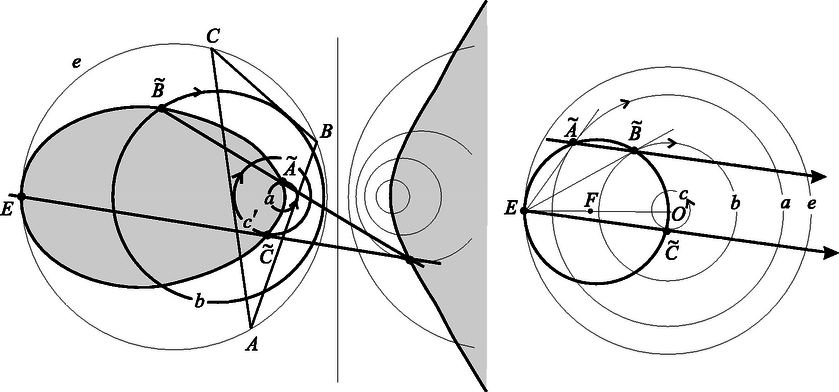
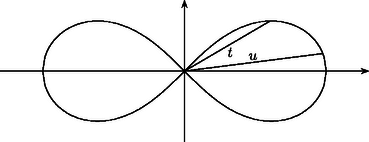
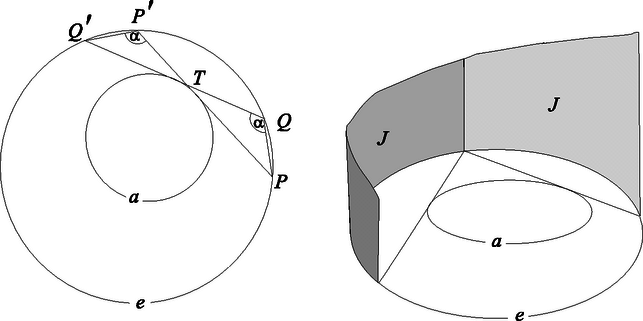
Tegyük fel most, hogy azt a feladatot kapjuk, hogy szerkesszünk háromszöget, ha adott körülírt és beírt körének sugara és a két középpont távolsága. A tétel alapján mondhatjuk, hogy ha a három adat nem teljesíti a (3) összefüggést, akkor nem létezik ilyen háromszög, ha viszont teljesíti, akkor a háromszög alulhatározott, végtelen sok megoldás van.
A helyzet ahhoz hasonló, mint mikor három szögből akarunk háromszöget szerkeszteni. Csak akkor van megoldás, ha a szögek összege

180^{\circ}

, ekkor viszont végtelen sok megoldás van. Sőt, a háromszög egyik oldalát ilyenkor tetszőlegesen felvehetjük, mindig találunk megoldást. Éppen így, ha az

e

és

a

körök

R

r

sugarai és középpontjuk

d

távolsága kielégíti a (3) egyenletet, akkor az

e

kör bármely pontja felvehető egy

e

-be és

a

köré írt háromszög csúcsaként. Ez az állítás persze indoklásra szorul, ehhez hozzásegít pl. a 3. feladat. Az előző állításból és Euler tételéből már következik Poncelet tétele az

n = 3

esetre: csak a (3) feltétel teljesülése esetén záródhat a poligon három lépésben, akkor viszont akárhonnan indulva záródik.(4. ábra).
Hogyan nem léteznek a (3) egyenletnek nem megfelelő adatokból szerkesztendő háromszögek? Poncelet bizonyításának lépései és könyvének bevezetőjében a szerkesztő eszközök beszerzésének nehézségeiről valló panaszai alapján úgy látom, hogy a rab mérnök erre a kérdésre kereste a választ.
Az 5. ábrán ilyen rossz adatokból próbáltunk háromszöget szerkeszteni. Az

e

a

köröket a rossz adatoknak megfelelően vettük fel. Az

e

kör egy próbaképp felvett

A

pontjából érintőt húztunk

a

-hoz, ami

e

-ből kimetszette a háromszög következő csúcsát,

B

-t. A

B

-ből

a

-hoz húzott másik érintő segítségével kaptuk

C

-t. Az

A C

egyenes láthatóan nem érinti

a

-t, tehát a szerkesztés nem volt sikeres. Több hasonló próbálkozás után Poncelet azt vehette észre (hiszen ezt bizonyította), hogy a kísérletezés során kapott

A C

egyenesek egyike sem érinti ugyan az

a

kört, de mindegyik érint egy bizonyos másik kört,

c

-t. Ráadásul ez a

c

kör az

e

és

a

generálta körsorhoz tartozik. Ez különösen feltűnő a háromszög szerkesztésének szempontjából eleve reménytelen

a

e

metsző körök esetén.)
Tehát a szerkesztendő háromszögek egyfajta nagyon szabályos módon nem léteznek. Euler tételéről kiderült, hogy nem egyszerűen csak a háromszögről és annak két köréről, hanem egy körsor elemei között kígyózó poligon záródásáról szól.
A megfigyelésekből adódik az előző szerkesztési feladat alábbi általánosítása.

Az adott

e

kör és a belsejében felvett

a

b

c

körök tartozzanak ugyanahhoz a körsorhoz. Szerkesztendő háromszög, melynek körülírt köre

e

A B

B C

A C

oldalai pedig rendre érintik az

a

b

c

köröket.

Egy külső pontból egy körhöz két érintő is húzható. Hogy az ebből fakadó szerkesztési bizonytalanságot megszüntessük, a feladatban rögzítsünk az

a

b

c

körökön egymástól függetlenül egy-egy forgásirányt, és követeljük meg, hogy a szerkesztendő

A B C

háromszög oldalain az

\vec{A B}

\vec{B C}

\vec{A C}

irányok mindhárom érintési pontnál egyezzenek meg a megfelelő érintő kör forgásirányával.
A szerkesztési feladat megoldása korábbi feladatunkéhoz hasonló, de a bizonyítás itt még nehezebb. (6. ábra).Most sem a szerkesztés okozza a nehézséget, hanem a diszkusszió: Ha az

e

a

b

c

körök (és az utóbbiak forgásiránya) megfelelő, akkor

e

bármely pontjából kiindulva az egyértelmű szerkesztési eljárás eredményeképp mindig háromszöget kapunk. Általában pedig itt is azt vehetjük észre, hogy a próbálkozások során kapott

A C

egyenesek mindig a körsor egy bizonyos

c^{'}

körét érintik, mindig ugyanabban a forgásirányban, de ez a

c^{'}

kör az esetek zömében nem egyezik meg

c

-vel. Most nem térünk ki rá, hogy mikor egyezik meg a

c^{'}

kör

c

-vel, éppen elég meglepő, hogy a

c^{'}

kör egyáltalán létezik.
Tekintsük most az

e

kör pontjainak halmazán azt a leképezést, amely az

X \in e

ponthoz hozzárendeli az

X

-ből az

a

(irányított) körhöz húzott, az irányításnak megfelelő érintő

e

-vel való második metszéspontját. Úgy tekintjük, hogy ha az

a

kör megegyezik

e

-vel, akkor ez a leképezés az identitás, azaz a helybenhagyás. Ha az

a

kör koncentrikus

e

-vel, de nem egyezik meg vele, akkor a vizsgált transzformáció egy egyszerű elforgatás. Más esetben csak a forgatáshoz hasonló hozzárendelést kapunk, nevezzük ezt a továbbiakban ferde elforgatásnak. Két, azonos pont körüli elforgatás egymás utáni elvégzésének eredőjeként (azaz a két elforgatás kompozíciójaként) újabb elforgatást kapunk, melynek szöge az eredeti forgási szögek összege. Előbb épp azt vettük észre, hogy ennek az állításnak az első fele általánosítható: az

a

irányított körre, majd a

b

irányított körre vonatkozó ferde elforgatások kompozíciója is egy ferde elforgatás, nevezetesen a fent említett

c^{'}

kör által meghatározott ferde elforgatás. Jacobi bizonyítása majd arra világít rá, hogy mi az a szám, az a mérték, ami az általános esetben a forgási szöget helyettesíti.
Mintha az

e

körből, a körsor

e

belsejében fekvő irányított köreiből és pontköréből (lásd a 2. feladatot), álló

P

halmazon lenne egy

⊛

művelet, ami a ferde elforgatások kompozíciójának felel meg:

\begin{matrix} \begin{matrix} a ⊛ b = c' . \end{matrix} \end{matrix}

Poncelet, bár szót sem ejtett ilyen absztrakt algebrai fogalmakról, lényegében mégis azt mutatta meg, hogy ez a

⊛

művelet asszociatív és kommutatív. (7. ábra):

\begin{matrix} a ⊛ b = b ⊛ a \end{matrix}

Ez azt jelenti, hogy a

P

halmaz a

⊛

műveletre nézve kommutatív, másként szólva Abel csoportot alkot, hiszen a maradék csoportaxiómák is teljesülnek:

e

az egységelem, és egy irányított kör inverze ugyanaz a kör az ellentétes irányításával.
Gondolatmenetének eredményeként Poncelet a korábban kimondottnál jóval általánosabb tételhez jutott el:

Poncelet általános tétele. Legyen

e

egy nem metsző körsor egyik köre, az

a_{1}

a_{2}

...

a_{n}

irányított körök pedig ugyanennek a körsornak

e

belsejében található nem feltétlenül különböző tagjai. Az

e

körön fölvett

A_{0}

pontból kiindulva megszerkesztjük az

A_{1}

A_{2}, ...

A_{n}

pontokat ugyanezen a körön úgy, hogy az

A_{0} A_{1}

A_{1} A_{2}, ...

A_{n - 1} A_{n}

egyenesek rendre érintsék az

a_{1}

a_{2}, ...

a_{n}

köröket, az irányításnak megfelelően. Előfordulhat, hogy a szerkesztés végén éppen visszajutunk, azaz

A_{n} = A_{0} .

Ebben az esetben az

e

kör bármelyik másik pontjából is indulunk ki, az

n

-edik lépés után vissza fogunk jutni a kezdőpontba és még arra sem kell ügyelnünk, hogy ugyanabban a sorrendben húzzuk az érintőket a megadott körökhöz.

Bizonyítás. Az

e

körvonal

a_{1}

a_{2}, ...

a_{n}

körökre vonatkozó ferde elforgatásainak kompozíciója a körsor

\begin{matrix} b = a_{1} ⊛ a_{2} ⊛ ... ⊛ a_{n} \end{matrix}

irányított köre által meghatározott ferde elforgatással egyezik meg. Ez a transzformáció az

A_{0}

pontot önmagára képezi, tehát a

b

irányított körhöz

A_{0}

-ból húzott érintő nem metszheti az

e

kört, hanem azt is érinti. Ez azt jelenti, hogy

b = e

, hiszen a körsor többi eleme

e

belsejében van és nem is érintheti

e

-t. Az

e

által meghatározott ferde forgatás az identitás, tehát az

A_{0}

pont helyett bármelyik másik pontból indulunk is ki, visszajutunk hozzá. A csoport kommutativitása miatt az se számít, hogy milyen sorrendben húzzuk az érintőket a megadott körökhöz.
Ha

a_{1} = a_{2} = ... = a_{n} = a

, akkor Poncelet korábban említett tételéhez jutunk. Ott nincs szükség a körök irányításának bevezetésére, mert ha az

a

kör (illetve az általános esetben az

a_{1}

a_{2} ...

a_{n}

körök mindegyikének) irányítását megfordítjuk, akkor ugyanazokat az érintőket kell megrajzolni, mint korábban, csak ellenkező irányban és fordított sorrendben.

Poncelet tétele és a harmadrendű görbe

Feleltessünk meg a

P

csoport elemeinek egy-egy pontot az alábbi módon. Válasszunk

e

-n egy tetszőleges

E

pontot

e

számára. A körsor egy tetszőleges irányított körének feleljen meg az

E

-ből hozzá (az irányításnak megfelelően) húzott érintő érintési pontja (8.a) ábra).
Az így kapott pontok egy harmadrendű görbe részhalmazát alkotják (lásd a 6. feladatot). Ha a görbe egységelemének az

E

pontot tekintjük, akkor a szóbanforgó részhalmaz egyben részcsoport is lesz és a

P

-beli

⊛

művelet és a harmadrendű görbe

*

művelete éppen megfelel egymásnak (8.b) ábra). Ezt az állítást itt nem bizonyítjuk.
Érdekesen lóg ki a sorból a koncentrikus körökből álló körsor esete. Ebben az esetben

P

elemei valódi forgatásoknak felelnek meg.
8.b) ábra. Ha

a ⊛ b = c'

, akkor az

E

-ből az

a

b

c'

körökhöz húzott érintők

\tilde{A}

\tilde{B}

\tilde{C}'

érintési pontjaira

\tilde{A} * \tilde{B} = \tilde{C}'

.
Az

E

-ből a körökhöz húzott érintők talppontjai első látásra nem harmadrendű görbét, hanem az

E O

szakasz

k

Thalesz-körét alkotják. Ha az

a

irányított körhöz hozzárendelt pont

\tilde{A}

, akkor a körnek megfelelő forgatás a

2 \cdot \tilde{A} O E ∢ = \tilde{A} F E ∢

-gel való forgatás, ahol

F

k

középpontját,

∢

az irányított szöget jelöli.
Tegyük fel, hogy ehhez a Thalesz körhöz tartozik még egy

l

egyenes is, nevezetesen az ideális egyenes. (A sugárnyaláb modellben úgy is fogalmazhatnánk, hogy mostani ábránk a teljes konfigurációnak csak egy rajza, amiről lemaradt az

l

egyenes, mert a rajzsík párhuzamosan áll az egyenesről szemünkbe jövő fénysugarak síkjával.) Az

l \cup k

ponthalmaz egy (reducibilis) harmadrendű görbe, hiszen polinomja egy másodfokú és egy elsőfokú polinom szorzata. A reducibilis görbén nem végezhető el korlátlanul a

*

művelet (pl. az egyenes két pontját most nem tudnánk összeszorozni), de az adott esetben

k

bármely két pontja össze-

*

-szorozható. Az

\tilde{A}

\tilde{B} \in k

pontok

\tilde{A} * \tilde{B}

szorzatát úgy kapjuk, hogy tekintjük az

\tilde{A} \tilde{B}

egyenes és

l \cup k

harmadik metszéspontját, tehát az

\tilde{A} \tilde{B}

egyenes ideális pontját; majd ezt összekötjük

E

-vel, azaz párhuzamost húzunk

\tilde{A} \tilde{B}

-vel

E

-n át és ez az egyenes kimetszi

k

-n

\tilde{A} * \tilde{B}

-t. A

*

és

⊛

műveletek egymásnak való megfelelése tehát az alábbi elemi állításon múlik:

Ha az

\tilde{A} \tilde{B} E

háromszög körülírt körének középpontja

F

és az

E \tilde{C}

húr párhuzamos az

\tilde{A} \tilde{B}

húrral, akkor

\begin{matrix} E F \tilde{A} ∢ + E F \tilde{B} ∢ = E F \tilde{C} ∢ (mod 2 π) . \end{matrix}

E szép állítás igazolását az olvasóra bízzuk.
Míg Poncelet 1822-ben publikálta poligonjait, a harmadrendű görbe csoporttulajdonságára csak 1835-ben derített fényt a königsbergi Jacobi. De előtte még neki is volt egy kalandja Poncelet tételével.

Elliptikus integrálok

1827-ben a Journal für die reine und angewandte Mathematik ⁴ folyóiratban az alábbi feladatot tűzte ki J. Steiner:

Egy ötszög egyszerre húr- és érintő-ötszög is. Milyen összefüggés áll fönn a két kör sugara és középpontjaik távolsága között? Oldjuk meg a feladatot

6

7

8

9

10

-szög esetére is.

Steiner tehát, Poncelet tételéhez kapcsolódva, a záródás algebrai feltételei iránt érdeklődött. Steiner tudta a megoldást ezekben az esetekben, de nemhiába tűzte ki a problémát, mert felkeltette Jacobi érdeklődését, aki így új, különleges bizonyítást adott Poncelet tételére.
Jacobi ekkortájt az elliptikus integrálokkal foglalkozott. Ez a problémakör G. Fagnano hercegnek az ellipszissel és a lemniszkáta görbével kapcsolatos eredményeiből született. Fagnano szerette volna meghatározni, hogy az

{(x^{2} + y^{2})}^{2} = x^{2} - y^{2}

egyenletű lemniszkáta origóból induló

t

hosszúságú húrjához mekkora lemniszkátaív tartozik. (9. ábra).Ezzel a problémával ekvivalens kérdéssel J. Bernoulli és L. Euler is találkozott rugalmasságtani vizsgálódásaik során. Egyiküknek se sikerült fölírni a lemniszkáta ívhosszát megadó

I (t)

függvényt.
Fagnano eredménye az volt, hogy meg tudta határozni, hogy milyen hosszú az a húr, amelyhez kétszer akkora ív tartozik, mint a

t

hosszúságú húrhoz. Euler messzemenően általánosította a módszert. Képletet, úgynevezett addíciós formulát, adott, amely a

t_{1}

t_{2}

számokból előállítja annak a húrnak a hosszát, amelyhez tartozó ív éppen olyan hosszú, mint a

t_{1}

és

t_{2}

hosszúságú húrok ívei összesen. Euler ezen is túl ment: megadta azoknak az ív- és területszámítási problémáknak (általánosabban: integráloknak) egy széles körét, ahol addíciós formula adható. Ezeket nevezzük elliptikus integráloknak.

Jacobi is jelentős eredményeket ért el ebben a témában. N. H. Abellel versengve írták a cikkeket az említett folyóiratban az elliptikus integrálokról. Jacobi, változatosságképpen, megpróbálkozott Steiner feladatával is. Ábrát készített, behúzott néhány vonalat, kifejezte a hosszukat és elámult: az elliptikus integrálok addíciós formuláihoz kísértetiesen hasonló képletek álltak előtte. A képletek azt mutatták, hogy van egy mennyiség, egy integrál, ami a Poncelet-poligon egyes oldalainak behúzásakor mindig ugyanannyival változik. A koncentrikus körök esetén ez a mennyiség a poligonhoz tartozó középponti szög. Ebben a speciális esetben ugyanis a két kör közötti minden ,,érintő húr" egyenlő hosszú, középponti szögeik is egyenlőek. Ha e középponti szög

n

-szerese

360^{\circ}

, vagy annak egész számú többszöröse, akkor a poligon

n

lépésben záródik, egyébként pedig nem.

Jacobi azt látta a képletekből, hogy az általános esetben is van egy, a középponti szögnek megfelelő mérték. A tétel bizonyításához nem volt lényeges, hogy mi ennek a mértéknek a geometriai tartalma. Ezt azért hangsúlyozzuk ennyire, mert az alább közölt bizonyítás logikus és szemléletes, de nem árt tudni, hogy aki kitalálta, az másfajta logikával, másfajta szemlélettel jött rá.

Jacobi bizonyítása

Szeretnénk a Poncelet tétel

e

alapkörén egy olyan mértéket bevezetni, amely a kör

P P^{'}

és

Q Q^{'}

ívéhez ugyanazt a számot rendeli, ha a

P P^{'}

egyenes és a

Q Q^{'}

egyenes is érinti az

a

kört.
Próbálkozzunk először egymáshoz közeli ívekkel. Az is jó lenne, ha a

P Q

P^{'} Q^{'}

ívek mértéke lenne egyenlő. Az említett ívek majdnem ugyanolyan hosszúak, mint a

P Q

P^{'} Q^{'}

szakaszok. Ezek a szakaszok, sajnos, nem egyenlő hosszúak, de egymással egyszerűen kapcsolatba hozhatók. A

P Q T

Q^{'} P^{'} T

háromszögek ugyanis az egyenlő kerületi szögek miatt hasonlóak. Ennek alapján

\begin{matrix} \frac{P Q}{P T} = \frac{P^{'} Q^{'}}{Q^{'} T} . \end{matrix}

(4)

Az egyenlet két oldalán a nevezők a

P Q

, illetve a

P^{'} Q^{'}

ív pontjaiból az

a

körhöz húzott érintőszakaszok hosszát közelítik. Ez azt jelenti, hogy ha egyenlő mértéket akarunk adni a

P Q

P^{'} Q^{'}

szemköztes íveknek, akkor mindkettőt a pontjaiból az

a

körhöz húzott érintő reciprokával kell súlyozni.
Ezt a gondolatot szemléletessé tehetjük. Emeljünk az

e

körre, a kör síkjára merőlegesen, hengerszerűen egy palástot. A palást alapja legyen maga a körvonal, a magassága viszont pontonként változzék. A kör

P

pontjában a palást magassága legyen egyenlő a

P

-ből az

a

körhöz húzott érintőszakasz hosszának reciprokával. A palást felszíne a keresett mérték.(10. ábra).
Állítjuk, hogy a

P Q

és a

P' Q'

ívekhez tartozó palástdarabok felszíne egyenlő. A (4) egyenlet két oldalán e palástrészek felszínének egy-egy közelítő értéke áll. A

P Q

és

P' Q'

szakaszok hossza a

P Q

P Q'

ívek hosszát,

\frac{1}{P T}

és

\frac{1}{Q' T}

értéke pedig a vizsgált ívek fölötti palást magasságát közelíti. E palástdarabok felszínére pontosabb értéket kapunk, ha a

P Q

ívet és vele szemben a

P' Q'

ívet kisebb darabokra osztjuk, és a kisebb részeket külön-külön becsüljük meg egy-egy húr és közelítő magasság szorzatával. Ha ezt mindig a (4) egyenlet két oldalának megfelelő formula segítségével tesszük, akkor a

P Q

ív és a

P' Q'

ív fölötti részekre mindig egyenlő közelítő értékeket kapunk. Ezzel a módszerrel a két palástrész felszínét tetszőleges pontossággal megközelíthetjük, ami csak úgy lehet, hogy ez a két rész egyenlő felszínű.
Eredményünkből következik, hogy a

P P'

és

Q Q'

ívekhez tartozó palástdarabok is egyenlő felszínűek. Képzeljük el, hogy a

P

P^{'}

pontokat úgy mozgatjuk az

e

körön, hogy a

P P^{'}

húr mindig érinti az

a

kört. Megállapításaink szerint eközben a

P P^{'}

ívhez tartozó palástrész területe mindig állandó marad. Jelölje ennek az állandónak az értékét

J

, a teljes palást területét

I

.
A Poncelet-poligon pontosan akkor záródik

n

lépésben

m

körbefordulás után, ha

m I = n J

. Ez a feltétel teljesen független az

A_{0}

kezdőpont megválasztásától,
így Poncelet tételét bebizonyítottuk. Azt is láthatjuk, hogy a poligon akkor fog záródni, ha a

\frac{J}{I}

hányados racionális és a visszatéréshez szükséges lépésszám ennek a racionális számnak a nevezője.
A Jacobi-féle palást területe olyan tulajdonságú, mint a lemniszkáta ívhossza. Egy rögzített pontból induló húrok hosszától való függése transzcendens, azaz véges sok elemi függvény segítségével nem fejezhető ki. De föl lehet írni a Fagnano-féle duplikációs képletnek megfelelő

n

-szerezési formulát, amivel Steiner problémája is teljes általánosságban megoldható. Ezt a munkát azonban, csak mintegy 25 évvel később, A. Cayley végezte el.
Jacobi módszere, egy kis módosítással, alkalmas Poncelet általános tételének bizonyítására is. Ennek érdekében rögzítsünk az

e

körön egy

E

pontot és a palást

P

pont fölötti magasságát definiáljuk úgy, mint az

E

ponttól, illetve a

P

ponttól az

a

körhöz húzott érintők arányát:

m (P) = \frac{E E_{A}}{P P_{A}} .

Ez a korábban definiált magasságtól csak az

E E_{A}

konstans szorzóban különbözik. Értelme az, hogy ez a magasság univerzális, a körsor minden eleme ugyanazt a palástot határozza meg. Ennek magyarázata egy korábbi eredményünkben rejlik. Láttuk, hogy ha

a

b

e

egy körsor három eleme, akkor

e

különböző pontjainak az

a

b

körökre vonatkozó hatványainak, esetünkben az érintő szakaszoknak, az aránya egyenlő:

\frac{E E_{A}}{E E_{B}} = \frac{P P_{A}}{P P_{B}}

, azaz

\frac{E E_{A}}{P P_{A}} = \frac{E E_{B}}{P P_{B}} .

Ha a teljes palást területe

I

, a körsor

a_{1}

a_{2}, ...

a_{n}

irányított elemeihez az érintők által meghatározott ívek fölötti palástdarabok területe

J_{1}

J_{2}, ...

J_{n}

akkor a záródás feltételét a

\begin{matrix} J_{1} + J_{2} + ... + J_{n} = m I \end{matrix}

egyenlet fogalmazza meg. Ennek az összefüggésnek a teljesülése pedig valóban független a kezdőpont választásától.

Feladatok

1. a) Mutassuk meg, hogy bármely körsor tagjainak középpontjai egy egyenesen helyezkednek el.
b) Legyen egy körsor egyik körének sugara

R

, a körsor egy másik, az előzőnél kisebb körének sugara

r

, a két középpont távolsága

d

. Bizonyítsuk be, hogy a

\begin{matrix} k = \sqrt[]{\frac{4 R d}{{(R + d)}^{2} - r^{2}}} \end{matrix}

értéke nem függ a kisebb kör választásától.
c) Mutassuk meg, hogy a körsor rendre akkor koncentrikus; nem metsző; érintő; metsző, ha

k = 0;

0 < k < 1;

k = 1;

1 < k .

2. Bizonyítsuk be, hogy a nem metsző; érintő; metsző körsorokban rendre 2; 1; 0 pontkör, azaz

{(x - u)}^{2} + {(y - v)}^{2} = 0

egyenletű alakzat található.

3. Az

A B C

háromszög körülírt köre

e

, beírt köre

a

. A két kör sugara

R,

illetve

r,

középpontjaik távolsága

d .

A beírt kör érintési pontjai

X,

Y,

Z .

a) Bizonyítsuk be, hogy az

a

körre vonatkozó inverziónál az

e

kör képének sugarát és középpontjának

a

középpontjától való távolságát az

\begin{matrix} R^{'} = \frac{R r^{2}}{R^{2} - d^{2}} d^{'} = \frac{d r^{2}}{R^{2} - d^{2}} \end{matrix}

képletek adják meg!
b) Bizonyítsuk be, hogy az

a

körre vonatkozó inverziónál az

A,

B,

C

pontok az

X Y Z

háromszög oldalfelezőpontjaiba képződnek.
c) Bizonyítsuk be Euler tételét!
d) Bizonyítsuk be Poncelet tételét az

n = 3

esetben!

4. Keressük meg az Euler tételének megfelelő formulát a háromszög körülírt és hozzáírt körére vonatkozólag!

5. a) Bizonyítsuk be, hogy az

a (x, y) = 0

b (x, y) = 0

körök generálta körsor

P (ξ, η)

ponton átmenő elemének egyenlete:

\begin{matrix} b (ξ, η) a (x, y) - a (ξ, η) b (x, y) = 0. \end{matrix}

b) Bizonyítsuk be, hogy az (1) egyenletű kört a

P (ξ, η)

pontjában érintő egyenes egyenlete:

\begin{matrix} (ξ - u_{a}) (x - ξ) + (η - v_{a}) (y - η) = 0. \end{matrix}

c) Bizonyítsuk be, hogy egy pontból egy körsor elemeihez húzott érintők érintési pontjai általában harmadrendű görbét alkotnak.

6. a) Írjuk föl az (1) egyenlet homogén megfelelőjét és mutassuk meg, hogy a körre illeszkednek az

(1, i, 0)

(1, - i, 0)

ideális és egyben képzetes (

i^{2} = - 1

) pontok.
b) Bizonyítsuk be, hogy egy valós együtthatós, nem üres irreducibilis másodrendű görbe pontosan akkor kör, ha illeszkednek rá az

(1, i, 0)

(1, - i, 0)

pontok. ⁵

Hraskó András

¹Murányi Beatrix fordítása

²Kiss György: A körre vonatkozó polaritás, KöMaL, 1998/8. szám, 450. o.

³a $P R \cdot P Q$ szorzatot előjelesen értelmezzük, tehát ha $P$ -től $R$ és $Q$ ellenkező irányban vannak, azaz ha $P$ a kör belső pontja, akkor a szorzat értéke negatív.

⁴A Tiszta és alkalmazott matematika lap című folyóiratot éppen Steiner és Abel ösztönzésére alapította A. L. Crelle porosz mérnök.

⁵A komplex számok bevezetése a geometriába szintén Poncelet hadifogságbeli töprengéseinek eredménye. Többek között ezt mondta: ha komplex koordinátákat is megengedünk, akkor bármely két másodrendű görbének létezik két közös pontja. Ha ezeket átvetítjük az $(1, i, 0)$ , $(1, - i, 0)$ pontokba, akkor a két görbéből két kört kapunk. Így a Poncelet tételt is elég két körre igazolni.