Kezdőlap


Cím:	Harmadrendű görbék
Szerző(k):	Hraskó András
Füzet:	2000/április, 193 - 204. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

...

számomra egy geometriai probléma megoldása egyenletekkel éppen olyan, mint egy fogantyú forgatásával játszani le egy dallamot. Amikor első alkalommal jutottam számítás útján arra az eredményre, hogy két tag négyzete a részek négyzetéből és kétszeres szorzatukból áll, akkor szorzásom kifogástalansága ellenére sem akartam elhinni ezt mindaddig, amíg ábráját el nem készítettem. Nem mintha nem lett volna nagy kedvem az algebrához mint az elvont mennyiségek tudományához, de a térben alkalmazva a műveleteket vonalakban akartam látni, másként nem értettem belőlük semmit. ¹
Jean-Jacques Rousseau: Vallomások

Descartes azzal, hogy megismertette a világgal koordinátarendszerét egyben kapcsolatot létesített a matematikán belül két terület, az algebra és a geometria között. Koordinátarendszerében az

5 x + 6 y - 7

kétváltozós elsőfokú polinomnak megfelel egy egyenes, a polinom zérushelyeinek halmaza, az

x^{2} + y^{2} - 1

másodfokú polinomnak egy kör.
A definiáló polinom foka alapján elsőrendű görbéknek nevezzük az egyeneseket, másodrendű görbéknek a kört, ellipszist, hiperbolát, parabolát és az egyenespárokat. Az egyenespárok egyenletében szereplő polinom a párt alkotó két egyenes polinomjának szorzata, ezért másodfokú. Az egyenespárok ennek alapján reducibilis, azaz felbontható görbék, hiszen előállíthatók náluk kisebb fokú görbék uniójaként. Ezzel szemben az összes korábban említett görbe irreducibilis, azaz felbonthatatlan.
A másodrendű görbéket (nem ezen az összefoglaló néven) már a görögök is jól ismerték, többek között azt is tudták róluk, hogy kúpszeletek. Kepler a Descartes-ot megelőző évszázadban adott különleges jelentőséget ennek a görbeosztálynak azzal, hogy rámutatott a bolygómozgásban játszott szerepükre. Descartes kortársai közül Desargues és Pascal tett sokat e görbék megismeréséért, az utóbbi nevezetes tételéről a KöMaL-ban is olvashattunk (1998/8., 454. o.)
De milyen görbét rejt magában az

x^{3} + y^{2} - 1

polinom? Hányféle harmadrendű görbe van? Milyen általános tulajdonságaik vannak? Hogyan olvashatók le speciális jellemzőik definiáló polinomjuk együtthatóiból? Mindezek a kérdések föl sem merülhettek Descartes előtt.
Már a XIX. században rájöttek, hogy Pascal tétele a harmadrendű görbékre vonatkozó egyik legalapvetőbb állítás speciális esete, és azóta már sok más geometriai összefüggésről is tudjuk, hogy olyan általános tételek speciális esetei, amelyek a harmadrendű görbe tulajdonságaival függenek össze. Néhány matematikus úgy egy évtizede rájött, hogy Descartes kortársának, Fermat-nak nevezetes sejtése bebizonyítható a harmadrendű görbe mélyebb ismerete alapján. Hiába olyan híres és friss ez az eredmény, ma, az internetes kereső programok a harmadrendű görbe angol megfelelőjére, az ,,elliptic curve" kulcsszóra többségében mégis olyan címeket írnak ki, melyek a kriptográfiáról, a titkosírás tudományáról szólnak. Ez a témakör éppen internetes felhasználása miatt népszerű. Lehet, hogy a harmadrendű görbe szerepet kap a modern kommunikációban?
Ebben a cikkben megpróbáljuk megérteni e manapság is széleskörűen vizsgált görbe néhány tulajdonságát.

A félszemű rajzoló

Vizsgálódásunkat egy klasszikus problémával kezdjük. Megkeressük az összes pitagoraszi számhármast, vagyis az

\begin{matrix} x^{2} + y^{2} - z^{2} = 0 \end{matrix}

(1)

egyenlet összes pozitív egész megoldásait. Mielőtt belemennénk a számelméleti részletekbe, megvizsgáljuk az (1) egyenletet algebrai és geometriai szemszögből, hogy bemutassuk rajta a hasonló típusú problémák kezelésének projektív geometriai megközelítési módját.
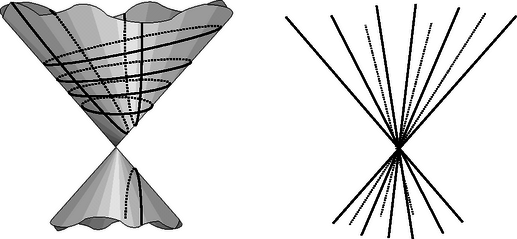
Az egyenlet bal oldalán szereplő

P (x, y, z)

polinom homogén, azaz a benne szereplő tagok mindegyikének ugyanakkora a foka. Ez azt jelenti, hogy ha a polinomban minden változó értékét ugyanazzal a

λ

számmal szorozzuk, akkor a kifejezés értéke

λ^{2}

-tel szorzódik:

P (λ x, λ y, λ z) = λ^{2} P (x, y, z)

. Következésképpen, ha

(x_{0}, y_{0}, z_{0})

megoldása az (1) egyenletnek, akkor

(λ x_{0}, λ y_{0}, λ z_{0})

is megoldás bármely

λ

esetén. Speciálisan, az egyenlet egy triviális megoldása a

(0, 0, 0)

számhármas.
Geometriai nézőpontból először is azt mondhatjuk, hogy az (1) egyenlet egy térbeli ponthalmaz egyenlete, hiszen a számhármasokat a tér pontjaival reprezentálhatjuk. A homogenitásból következik, hogy egy origó csúcsú kúpszerű alakzatról van szó, azaz bármely pontjával együtt a pontot az origóval összekötő egyenes is része a megoldáshalmaznak.
Tekintsünk úgy erre a kúpra, mint fénysugarak nyalábjára, melyek talán épp egy síkgörbéről érkeznek szemünkbe, az origóba. Ha magunk elé teszünk egy (nagyon nagy) papírt, a sugarak ezen kijelölnek egy görbét, a papír síkjának és a kúpnak a metszésvonalát. Olyan ez, mint amikor egy félszemű ember rajzol. ²
Persze, ha máshová helyezzük a papírt, azaz az origót nem tartalmazó másik síkkal metsszük a kúpot, akkor egy másik görbét fogunk kapni. A félszemű rajzoló nem tudja kitalálni a távoli görbe tényleges alakját, csak a látványról tud hűséges képet adni. Például abban sohasem lehet biztos, hogy kört lát-e, de fel tudja ismerni az egyenest (ha megmondják neki, hogy síkbeli alakzatról van szó). Általánosabban, azt is meg tudja mondani, hogy hányadrendű görbét lát, hiszen a rend a szemébe érkező fénysugarak által meghatározott kúpfelület tulajdonsága. Ha pedig egy egyenest és egy másik (algebrai) görbét is érzékel, akkor el tudja dönteni, hogy egy adott (látott) pontban metszik, vagy pedig érintik egymást.
Tehát a homogén polinomok fent leírt geometriájában, amit a projektív geometria sugárnyaláb modelljének is hívnak, a pontokat a tér origón átmenő egyeneseiként érzékeljük. Amíg szokásos (affin) értelemben

n

-edrendű síkgörbén egy két ismeretlenes

n

-edfokú polinomot, illetve a polinom zérushelyeinek halmazát értjük, addig a projektív megközelítésben

n

-edrendű síkgörbéről beszélve egy háromváltozós homogén

n

-edfokú polinomra és annak zérushelyeire gondolunk.

Másodrendű görbék számelmélete

Vegyük észre, hogy ha

(x_{0}, y_{0}, z_{0})

nem a triviális (azonosan 0) pitagoraszi számhármas, akkor az

\tilde{x_{0}} = \frac{x_{0}}{z_{0}}

\tilde{y_{0}} = \frac{y_{0}}{z_{0}}

racionális számpárra

\begin{matrix} {\tilde{x}}^{2} + {\tilde{y}}^{2} - 1 = 0. \end{matrix}

(2)

Másrészt, ha

(\tilde{x}, \tilde{y})

a (2) egyenlet racionális megoldásai, akkor a

(z \cdot \tilde{x}, z \cdot \tilde{y}, z)

az (1) egyenlet racionális megoldásai lesznek bármely

z

racionális szám esetén. Ha itt

z

\tilde{x}

\tilde{y}

törtek nevezőinek legkisebb közös többszöröse, akkor az (1) olyan egész megoldásait kapjuk, amelyben a tagok relatív prímek. Az ilyen számhármasokat nevezik az (1) egyenlet alapmegoldásainak.
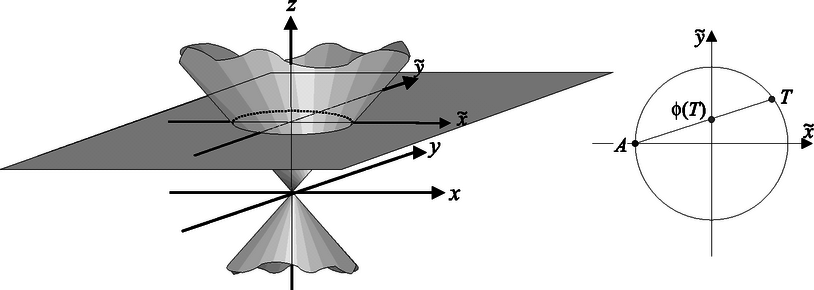
Most már csak a (2) egyenlet racionális megoldásait keressük, azaz kúpunk és a

z = 1

egyenletű

Π

sík metszésvonalának racionális koordinátájú pontjait.
Ez a metszésvonal egy egység sugarú kör. Tekintsük a kör

A (- 1; 0)

pontját és a kör többi pontját vetítsük

A

-ból az

\tilde{y}

tengelyre, azaz a kör

T

pontjának feleltessük meg az

\tilde{y}

tengelynek azt a

ϕ (T)

pontját, amely illeszkedik az

A T

egyenesre. A

ϕ

leképezés kölcsönösen egyértelmű hozzárendelést ad meg a kör

A

-tól különböző pontjainak halmaza és az

\tilde{y}

tengely pontjainak halmaza között. Állítjuk, hogy ezen belül a kör racionális pontjai a tengely racionális pontjainak felelnek meg.
Valóban, ha

T ({\tilde{x}}_{0}; {\tilde{y}}_{0})

racionális pont, akkor

ϕ (T)

ordinátája épp az

A T

egyenes meredeksége, nevezetesen

\frac{{\tilde{y}}_{0}}{{\tilde{x}}_{0} + 1}

, azaz racionális.
Másrészt, a tengely racionális pontját

A

-val összekötő egyenes egyenletének együtthatói két pontjának koordinátáiból alapműveletekkel számíthatók ki, így racionálisak. Az egyenes és a kör metszéspontjainak kiszámítása ugyan másodfokú egyenletre vezet, de ennek egyik gyöke az

A

pont megfelelő koordinátája, ami racionális. A keresett másik gyök bármelyik Vita-formulából alapművelettel meghatározható, így az is racionális. A konkrét számolást a pitagoraszi számhármasokat előállító formula kedvéért el is végezzük.
Ha

ϕ (T)

ordinátája

r = \frac{m}{n}

(

m \in Z

n \in Z^{+}

(m, n) = 1

, vagy

m = 0

és

n = 1

), akkor

T

koordinátáit úgy kaphatjuk, hogy az

A T

egyenes

\begin{matrix} \tilde{y} = r (\tilde{x} + 1) \end{matrix}

(3)

egyenletének jobb oldalával helyettesítjük

\tilde{y}

-t a (2) egyenletben. A két gyök szorzata az

\begin{matrix} (r^{2} + 1) {\tilde{x}}^{2} + 2 r^{2} \tilde{x} + (r^{2} - 1) = 0 \end{matrix}

(4)

egyenletben:

(- 1) \cdot {\tilde{x}}_{0} = \frac{r^{2} - 1}{r^{2} + 1}

, ahonnan (3) alapján

{\tilde{y}}_{0}

is adódik:

\begin{matrix} {\tilde{x}}_{0} = \frac{n^{2} - m^{2}}{n^{2} + m^{2}}, {\tilde{y}}_{0} = \frac{2 n m}{n^{2} + m^{2}} . \end{matrix}

Tehát

x_{0} = {\tilde{x}}_{0}

y_{0} = {\tilde{y}}_{0}

z_{0} = 1

az (1) egyenlet racionális megoldásai a

z = 1

egyenletű

Π

síkban. Az (1) egyenlet egész megoldásait úgy kapjuk, hogy a most kapott törteket szorozzuk a közös nevezővel, illetve annak bármely többszörösével.
Nem nehéz igazolni, hogy ha

(m, n) = 1

, akkor a kapott törtek nem egyszerűsíthetőek, ha

m

és

n

paritása különböző, illetve csak

2

-vel egyszerűsíthetőek, ha

n

és

m

is páratlan. Ennek alapján kaphatjuk meg az (1) egyenlet alapmegoldásait szolgáltató jól ismert képleteket:

\begin{matrix} x_{0} = n^{2} - m^{2}, y_{0} = 2 n m, z_{0} = n^{2} + m^{2}, \end{matrix}

(5)

n

és

m

paritása különböző, illetve

\begin{matrix} x_{0} = \frac{n^{2} - m^{2}}{2}, y_{0} = n m, z_{0} = \frac{n^{2} + m^{2}}{2}, \end{matrix}

(6)

n

és

m

páratlanok. Minden további megoldás úgy kapható, hogy ezen számhármasok valamelyikét egy egész számmal szorozzuk. Ha

x_{0}

és

y_{0}

sorrendje nem érdekes, akkor itt minden megoldás kétszer van fölsorolva: egyszer fent, egyszer lent. Fönt ugyanis

x_{0}

páratlan és

y_{0}

páros, míg lent éppen fordítva van. Ha feltesszük azt is, hogy

n > m

, akkor a negatív megoldásoktól is megszabadulunk.

n = 3

m = 1

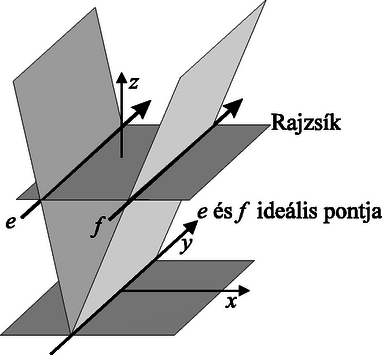
esetén kapjuk a nevezetes

4

3

5

számhármast.
A megoldás lényege a

ϕ

bijekció volt, amely a kör racionális pontjai és az egyenes racionális pontjai között teremtett egy-egyértelmű megfeleltetést. Ilyen megfeleltetés minden racionális együtthatós irreducibilis másodrendű görbe esetén megadható, ha találunk a görbén egyetlen racionális pontot, a vetítés centrumát. Tehát, ha egy racionális együtthatós másodrendű görbén van legalább egy racionális pont, akkor végtelen sok van belőle.
Sokkal nehezebb azt eldönteni, hogy létezik-e egyáltalán ilyen pont egy adott másodrendű görbén. Erre először Legendre talált módszert a XIX. század elején, amit a XX. század első felében Hasse és Minkowski általánosított több változó esetére.

Egyenesek, ideális pontok

Térjünk most vissza a

Π

rajzsíkra és tekintsük rajta az egymással párhuzamos

\tilde{x} - a = 0

egyeneseket. Ha az

a

paraméter értékét változtatjuk, akkor egymással párhuzamos egyeneseket kapunk. Ha kiválasztjuk ezen egyenesek bármelyikét és az origóból a kiválasztott egyenes (pozitív irányban) egyre távolabbi pontjai felé nézünk, akkor tekintetünk az

y

tengely (pozitív) irányát közelíti meg. Mintha ebben az irányban lenne a vizsgált egyeneseknek egy közös ,,végtelen távoli" pontja. Ha negatív irányba fordulunk az egyenesek távoli pontjai felé, akkor tekintetünk ugyanazt az egyenest, de épp az ellenkező irányt (ugyanazt a ,,fénysugarat") közelíti meg.
Algebrailag is eljuthatunk a ,,végtelen távoli" pont fogalmához. Ahogyan az

x^{2} + y^{2} - z^{2} = 0

egyenletből nyertük a

Π

síkban az

{\tilde{x}}^{2} + {\tilde{y}}^{2} - 1 = 0

egyenletet, ugyanúgy az

\tilde{x} - a = 0

egyenlet ,,hátterében" az

x - a z = 0

homogén egyenlet áll. Ezen egyenleteknek van közös megoldása például a

(0; 1; 0)

számhármas (értsd

x = z = 0

, és

y = 1

), de az

y

tengely bármely másik pontja is megfelelő.
A sugárnyaláb modellben az egyenesek homogén elsőfokú egyenleteknek felelnek meg, amelyek megoldáshalmaza a térben egy-egy origón átmenő sík. Bármely két origón átmenő síknak van metszésvonala, egy origón átmenő egyenes, egy ,,fénysugár". Így a projektív geometriában bármely két egyenesnek van metszéspontja. De előfordul, hogy egy-egy ,,rajzon", tehát az origót nem tartalmazó síkmetszeten két egyenes nem találkozik, párhuzamos. Ekkor azt is mondhatjuk, hogy ezek ez egyenesek a sík egy végtelen távoli, ideális pontjában metszik egymást. A rajzsíkon minden irányhoz tartozik egy ideális pont (az egymással ellentétes irányokhoz ugyanaz), ami a modellben az origóból induló, az adott iránnyal párhuzamos fénysugár. A rajzsík ideális pontjaihoz tartozó fénysugarak a rajzsíkkal párhuzamos, origón átmenő síkban fekszenek, tehát ‐ projektív értelemben ‐ egy egyenesen, az ideális egyenesen vannak.

Szinguláris harmadrendű görbék

A harmadrendű görbék racionális pontjai csak egyes speciális esetekben feleltethetők meg az egyenes racionális pontjainak úgy, ahogy a másodrendű görbéknél láttuk. Hiába találjuk meg ugyanis a görbe egy racionális pontját, az ezen átmenő, a görbét még egyszer metsző egyenesek általában még harmadszor is metszik a görbét. Így magát a

ϕ

leképezést meg tudnánk adni, bár a görbe két-két racionális pontjához rendelnénk az egyenes egy racionális pontját, de az inverz megfeleltetéssel gondunk lenne. Gondoljuk meg, most a (4) egyenlet helyén egy harmadfokú egyenlet áll, amelynek csak egy gyökét ismerjük így a másik kettő meghatározásához az általános eljárásban gyökvonásra is szükség lenne. Ez pedig bajba sodorja a racionalitást.
Más a helyzet az úgynevezett szinguláris görbéknél, azaz azoknál a harmadrendű görbéknél, amelyeken található szinguláris, azaz kettős pont. A harmadrendű görbe

P (x_{0}, y_{0})

pontját akkor nevezzük szingulárisnak, ha a rajta áthaladó egyenesek a görbét még legfeljebb egy pontban metszik. Ez úgy eshet meg, hogy a fent leírt metszéspont számítási eljárásban a (4) helyett kapott harmadfokú egyenletnek

x_{0}

minden esetben legalább kettős gyöke, és így a harmadik gyök az egyenlet együtthatóiból a Vita-formulák segítségével gyökvonás nélkül meghatározható, így racionális lesz. Ekkor, ha

x_{0}

y_{0}

és a görbe együtthatói is racionális számok, úgy alkalmazható a másodrendű görbéknél látott megfeleltetés.
Erre nemrég láttunk példát a KöMaL-ban, az egyik feladat megoldásában. Elevenítsük föl a feladatot.

F. 3278. Az

y = x^{3}

görbe pontjain egy

*

műveletet értelmezünk a következőképpen. Ha

A

és

B

a görbe két pontja, akkor legyen

A * B

A B

egyenes és a görbe harmadik metszéspontjának az origóra vonatkozó tükörképe. (Ha a definícióban szereplő valamelyik két pont egybeesik, akkor összekötő egyenesük helyett vegyük a görbe adott pontbeli érintőjét). Mutassuk meg, hogy a

*

művelet asszociatív.

A KöMaL 2000. évi első számának 28. oldalán megjelent megoldásban Székelyhidi Gábor és Terpai Tamás hozzárendelték a görbe

A (a; a^{3})

pontjához annak

x

tengelyre vonatkozó

ϕ (A) = a

merőleges vetületét és megmutatták, hogy ez a leképezés a görbe pontjait kölcsönösen egyértelmű megfeleltetésbe hozza a valós számokkal és a

*

műveletnek a valós számok összeadása felel meg.
Nyilvánvaló, hogy itt is megfeleltettük egymásnak a görbe és az egyenes racionális pontjait, de nem világos, hogy hol van a szinguláris pont. Végtelen messze van, de már közel vagyunk hozzá, hogy meglássuk.
Az

\tilde{y} = {\tilde{x}}^{3}

egyenlet homogén megfelelője az

y z^{2} - x^{3} = 0

egyenlet. Ennek megoldása az

(0; 1; 0)

számhármas, tehát a feladatban vizsgált

\tilde{y} - {\tilde{x}}^{3} = 0

görbének pontja az

\tilde{y}

tengellyel párhuzamos egyenesek ideális pontja. A közölt megoldásban alkalmazott

\tilde{x}

tengelyre való merőleges vetítés nem más, mint ebből az ideális pontból való vetítés.
Az ideális pont szingularitásának vizsgálatához egy másik rajzot készítsünk ugyanerről a görbéről, most az

y = 1

egyenletű síkban. Itt görbénk egyenlete

{\tilde{z}}^{' 2} - {\tilde{x}}^{' 3} = 0

, a korábban talált ideális pont itt az origó. Ez a pont szinguláris, hiszen az origón áthaladó

\tilde{z}' = r \tilde{x}'

egyenes és a görbe metszéspontjaira:

r {\tilde{x}}^{' 2} - {\tilde{x}}^{' 3}

, aminek

\tilde{x}' = 0

mindig legalább kétszeres gyöke.

4. ábra. Az

y z^{2} = x^{3}

kúp egy részlete és két ,,rajza"

Javaslom, hogy az olvasó próbálkozzék először maga az előbb említett feladat alábbi variációjával:

F. 3278

'

. Az

x y = {(x - 1)}^{3}

görbe pontjain értelmezzük a

*

műveletet a következőképpen. Ha

A

és

B

a görbe két pontja, akkor jelölje

C

A B

egyenes és a görbe harmadik metszéspontját,

A * B

pedig legyen

C

-t a görbe

E (1; 0)

pontjával összekötő egyenes és a görbe harmadik metszéspontja. (Ha a definícióban szereplő valamelyik két pont egybeesik, akkor összekötő egyenesük helyett vegyük a görbe adott pontbeli érintőjét). Mutassuk meg, hogy a

*

művelet asszociatív.

Az alábbi bizonyítást az F. 3278. feladat már említett megoldásának mintájára végezzük.

Görbénk pontjait egyértelműen jellemezhetjük abszcisszájukkal. Ez még világosabban látszik az eredetivel ekvivalens

\begin{matrix} y = \frac{{(x - 1)}^{3}}{x} x \neq 0 \end{matrix}

egyenletből.

Legyen

⊙

az a művelet a valós számok halmazán, amely a görbe

a

és

b

abszcisszájú

A

és

B

pontjai esetén

a ⊙ b

-nek az

A * B

pont abszcisszáját felelteti meg. A

*

művelet pontosan akkor asszociatív, ha a

⊙

művelet is az a

R ∖ {0}

halmazon. Megmutatjuk, hogy

⊙

épp a szorzás, amiből az állítás következik.
Ha az

A

B

C

különböző pontok görbénkre és az

y = α x + β

egyenesre is illeszkednek, akkor

a

b

c

abszcisszáik kielégítik az

\begin{matrix} x (α x + β) = {(x - 1)}^{3} \end{matrix}

(7)

egyenletet. A gyökök és együtthatók közti összefüggések alapján

\begin{matrix} 1 = a \cdot b \cdot c . \end{matrix}

((7)-et és a vele ekvivalens

0 = (x - a) (x - b) (x - c)

egyenlet konstans tagjait hasonlítottuk össze.) Ugyanezt a gondolatmenetet alkalmazhatjuk a

C

E

A * B

pontokra, amiből kapjuk, hogy

\begin{matrix} 1 = c \cdot 1 \cdot (a ⊙ b) . \end{matrix}

A két egyenlet összevetéséből adódik, hogy

a ⊙ b = a \cdot b

, amint azt korábban állítottuk.

5. ábra.

A * B = D

, azaz

2 \cdot (- 1) = - 2

és

C * C = G

, azaz

{(- \frac{1}{2})}^{2} = \frac{1}{4}

Az állítás akkor is érvényes, ha bizonyos pontok, pl.

A

és

B

, egybeesnek. Ilyenkor az

A B

egyenes ,,határhelyzeteként" a görbe

A

pontbeli érintőjét húzzuk meg, azt az

y = α x + β

egyenletű egyenest, amelyre a (7) egyenletnek az

a

abszcissza legalább kétszeres gyöke. Így az általános esethez hasonlóan alkalmazhatjuk a (7) egyenletet a további számolásokhoz.
Ebben a feladatban is az

x

tengelyre merőleges vetítést alkalmaztunk, amely fölfogható a görbe

(0; 1; 0)

ideális és egyben szinguláris pontjából való vetítésként. A görbe és az egyenes racionális pontjai most is egymásnak felelnek meg.
A görbe homogén egyenlete:

x y z - {(x - z)}^{3} = 0

. Ezt valóban kielégíti a

(0; 1; 0)

számhármas. Az

y = 1

síkmetszeten az origóba kerül a szinguláris pont. A görbe egyenlete itt:

\tilde{x} \tilde{z} = {(\tilde{x} - \tilde{z})}^{3}

. Jobban megérthető a görbe viselkedése, ha áttérünk az

u = \tilde{x} - \tilde{z}

v = \tilde{x} + \tilde{z}

változókra, ami a koordinátarendszer

45^{\circ}

-os forgatását és

\frac{1}{\sqrt[]{2}}

arányú nyújtását jelenti. Itt az egyenlet:

v^{2} = u^{2} \cdot (1 + 4 u)

, amiből leolvasható, hogy az

u

változó

- \frac{1}{4}

és

0

közötti és a pozitív értékeihez

v

-nek két értéke is tartozik, míg

u = - \frac{1}{4}

-hez és

u = 0

-hoz csak

v = 0

megfelelő. A grafikon

u = - \frac{1}{4}

-nál ,,megfordul",

u = 0

-nál pedig ,,önmagát metszi". Itt máshogy ,,néz ki" a szingularitás.
Egyszer összeadás és egyszer szorzás. És ezek még csak a szinguláris görbék!

Harmadrendű görbe mint csoport

A szinguláris ponttal nem rendelkező, ezért nem szingulárisnak is nevezett görbék nem vetíthetők kölcsönösen egyértelmű módon az egyenesre, de a szingulárisakéhoz hasonló (projektív) geometriai úton definiálható, csak még rejtélyesebb műveleti tulajdonságaik vannak.

Tétel. Bármely irreducibilis harmadrendű görbe, és annak tetszőleges

E

nemszinguláris pontja esetén a görbe nemszinguláris pontjain az F. 3278

'

. feladatban leírt módon értelmezett

*

művelet az alábbi tulajdonságokkal bír:

*	$1.$ asszociatív;

*	$2.$ $E * A = A * E = A$ , a görbe bármely $A$ pontja esetén. (Azaz az $E$ pont úgy viselkedik, mint az összeadásnál a $0$ , vagy mint a szorzásnál az $1$ .

*	$3.$ Bármely $A$ pontnak van inverze (mint az összeadásnál az ellentett, a szorzásnál a reciprok), azaz olyan $A^{- 1}$ pont, amelyre $A * A^{- 1} = A^{- 1} * A = E$ .

Ha egy halmazon értelmezett kétváltozós művelet a fenti (1., 2., 3.) tulajdonságokkal rendelkezik, akkor azt mondjuk, hogy a halmaz a műveletre nézve csoportot alkot. A tétel lényegében azt mondja ki, hogy a harmadrendű görbe nemszinguláris pontjainak

E_{R}

halmaza a

*

műveletre nézve csoportot alkot. Ez a csoport a

*

művelet definíciójának egyenes következményeként még kommutatív is, azaz

A * B = B * A

bármely

A

és

B

pont esetén.
A fenti tételt itt nem bizonyítjuk. Az állítás számelméleti jelentősége abban van, hogy ha a görbe egyenletének együtthatói és az

E

pont koordinátái is racionális számok, akkor a görbe racionális pontjai egymás között ,,

*

-szorzódnak". Valóban, ha

A

és

B

koordinátái racionálisak, akkor az

A B

egyenes együtthatói is azok, így az F. 3278

'

. feladat megoldásában leírt módon a racionális koordináták és együtthatókkal végzett alapműveletekkel meghatározhatók a

C

, majd az

A * B

pont koordinátái is. Tehát a görbe racionális pontjainak

E_{Q}

halmaza is csoport a

*

műveletre nézve, az

E_{R}

csoport egy részcsoportja.
Lássunk egy konkrét példát. A 2000 évi Arany Dániel Matematikaverseny Kezdők kategóriájának 3. feladata így szólt:
Bizonyítsd be, hogy három egymást követő pozitív egész szám szorzata nem lehet köbszám.
Nem nehéz megmutatni, hogy három egymást követő egész szám szorzata csak akkor lehet köbszám, ha

0

ez a szorzat.
Most általánosítjuk ezt a kérdést. Lehet-e egy egész számokból álló háromelemű számtani sorozat tagjainak szorzata

0

-tól különböző köbszám?
Jelöljük a sorozat középső elemét

z

-vel, a differenciát

y

-nal, a szorzatként kapott szám köbgyökét

x

-szel. Az

(z - y) z (z + y) = x^{3}

egyenlet egész megoldásait keressük. Tekintsük az ezzel ekvivalens

x^{3} + z y^{2} - z^{3} = 0

homogén egyenletet, és térjünk át a

z = 1

síkon található rajzra. Most már a

\begin{matrix} {\tilde{x}}^{3} + {\tilde{y}}^{2} - 1 = 0 \end{matrix}

(8)

görbe racionális pontjait keressük.
Van négy kézenfekvő megoldás:

A (1; 0)

B (0; 1)

C (0; - 1)

és a homogén egyenletre visszapillantva láthatjuk, hogy az

\tilde{y}

tengely

E

ideális pontja most is megfelelő. Mindezek azonban olyan megoldáshoz tartoznak, amelyben a köbszám a

0

.
Keressük meg az

A B

egyenes és a görbe harmadik metszéspontját! Így a

D (- 2; 3)

pontot kapjuk, ami valódi megoldást ad feladatunkra:

(1 - 3) \cdot 1 \cdot (1 + 3) = {(- 2)}^{3}

E D

és

A C

is az

F (- 2; - 3)

pontban metszi a görbét, ami az előző megoldást adja, csak a tényezők sorrendje más. Próbálkozzunk még a görbe érintőivel!
A

B

pontbeli érintő az az

y = r \tilde{x} + 1

alakú egyenes, amelyre a

{\tilde{x}}^{3} + {(r \tilde{x} + 1)}^{2} - 1

polinomnak, azaz

{\tilde{x}}^{3} + r^{2} {\tilde{x}}^{2} + 2 r \tilde{x}

-nek a

0

kétszeres gyöke. Ezért

r = 0

, amiből azt kapjuk, hogy a görbe és az érintő metszéspontjainak

\tilde{x}

koordinátái kielégítik az

{\tilde{x}}^{3} = 0

egyenletet. Itt tehát egy harmadrendű érintésről (inflexiós pontról) van szó, az érintőnek más közös pontja nincs a görbével. Ugyanez a helyzet ‐ más ,,rajzon" számolva ‐ az

E

pontbeli érintővel, a

D

-beli érintő pedig

C

-n megy át. Több megoldást nem, de egy szép geometriai konfigurációt kaptunk. Csoportunkban:

D * D = B

D * D * D = B * D = A

D * D * D * D = A * D = C

D * D * D * D * D = C * D = F

, végül

D * D * D * D * D * D = E

.
Van-e más megoldás? Ez általában nagyon nehéz kérdés. A konkrét esetben talán eldönthető, de a szerző sem tudja pontosan a választ.
A hat vizsgált pont az

E_{R}

(és az

E_{Q}

) csoport egy részcsoportját alkotja, lehet, hogy a teljes

E_{Q}

-t. Ilyen hatelemű részcsoport a valós számokon belül sem az összeadásnál, sem a szorzásnál nincsen, most vizsgált görbénk algebrai struktúrája különbözik az előzőekétől.
Nézzünk egy másik példát! Nevezetes, hogy az

\begin{matrix} x^{3} + y^{3} = z^{3} \end{matrix}

(9)

egyenletnek az egész számok halmazán csak a triviális

(0; 0; 0)

és a

(0; 1; 1)

(1; 0; 1)

alapmegoldásai vannak. Ezt P. Fermat állította, miután elolvasta Diophantosz: Arithmetica című könyvében a pitagoraszi számhármasokról szóló részt. Tovább is általánosított, nevezetes sejtése azt mondja ki, hogy az

x^{n} + y^{n} = z^{n}

egyenletnek

n > 2

esetén csak olyan megoldásai vannak, amelyben legalább az egyik változó értéke

0

. Hogy lássuk, milyen éles is Fermat sejtése vizsgáljuk meg a (9) egyenlettől alig különböző

\begin{matrix} 7 x^{3} + y^{3} = z^{3} \end{matrix}

(10)

diofantikus egyenletet!
Vegyük észre, hogy most

E (0; 1; 1)

mellett

A (1; 1; 2)

is megoldás. Így a már ismertetett geometriai módszerekkel bármelyik rajzon számolva meghatározhatjuk

A

*

-hatványait" (vagy ,,

*

-többszöröseit", ahogy tetszik). Az alábbi értéket egy konkrét rajzon véghezvitt számolást követően, a közös nevezővel való átszorzás útján nyertük:

\begin{matrix} \begin{matrix} A * A (- 4; 3; 5), A * A * A (- 73; 38; 17), A * A * A * A (- 1265; 183; - 1256), \\ A * A * A * A * A (65882; 40049; 90271), \\ A * A * A * A * A * A (- 4381019; 4989780; 9226981), ... \end{matrix} \end{matrix}

Ebben az esetben alapmegoldások végtelen sorát kapjuk.
A XX. század elején Mordell bebizonyította, hogy a nemszinguláris harmadrendű görbén mindig kiválasztható véges sok racionális pont úgy, hogy a görbe bármely racionális pontja megkapható legyen ezekből kiindulva, már megtalált pontok összekötésével, megtalált pontbeli érintők behúzásával, ezeknek és a görbe harmadik metszéspontjának megkeresésével.
Mordell azt is sejtette, hogy csak véges sok racionális pont lehet mindazokon a

3

-nál magasabbfokú görbéken (affin görbéken, azaz bármelyik ,,rajzon") amelyek nem hozhatók a cikkben leírt

ϕ

bijekcióhoz hasonló megfeleltetésbe az egyenessel vagy valamely harmadrendű görbével. Ezt

1984

-ben Gerd Faltingsnak sikerült igazolnia. Ez egyben azt is jelentette, hogy a Fermat-féle egyenletnek

n > 3

esetén csak véges sok alapmegoldása lehet. Mégsem Faltings megközelítése vezetett el a Fermat sejtés megoldásához.
A harmadrendű görbék kaptak döntő szerepet a megoldásban, amikor ugyanabban az évben,

1984

-ben Gerhard Frey rámutatott, hogy ha a Fermat egyenletnek létezik a nemtriviális

A^{n} + B^{n} = C^{n}

megoldása, akkor az

y^{2} = x^{3} + (A^{n} - B^{n}) x^{2} - A^{n} B^{n}

harmadrendű görbe ellenpéldát adna Taniyama és Shimura egy sejtésére. Andrew Wiles

1993

-ban ez utóbbi sejtés igazolásával egyúttal bebizonyította Fermat állítását is.
Mindazok, akik idáig jutottak a cikk olvasásában bizonyára nagy örömüket fogják lelni Rónyai Lajos: Egy igazán csudálatos bizonyítás című írásában, amely a Hódi Endre szerkesztette Matematikai mozaikban jelent meg (Typotex Kiadó, 1999), és Simon Singh: A nagy Fermat-sejtés címen megjelent könyvében (Park Kiadó, 1997). A témához kapcsolódik még Kollár János: Algebrai geometria című cikke a Természet Világa Matematika Különszámában (1998).

Feladatok

1. Az 1, 25, és a 49 olyan négyzetszámok, amelyek egyben egy számtani sorozat egymást követő elemei. Állítsuk elő az összes ilyen számhármast.

2. Bizonyítsuk be, hogy irreducibilis harmadrendű görbének csak legfeljebb egy szinguláris pontja lehet.

3. Keressünk 7, egészekből álló megoldást az

y^{2} = 6 (x^{3} - x)

egyenlethez. Keressünk még 4 megoldást a racionális számok halmazán.

4. Keressünk olyan négy elemből álló számtani sorozatokat, amelynek tagjai közül kiválasztható három olyan, amelyek szorzata köbszám!

Ajánlott internet címek

Fermat tétele:
http://www.mbay.net/

\sim

cgd/flt/flt01.htm
http://www-groups.dcs.st-and.ac.uk/

\sim

history/HistTopics/
Fermat's

_

last

_

theorem.html
http://www.prometheus.demon.co.uk/01/01fermat.htm
http://mathworld.wolfram.com/FermatsLastTheorem.html
Kriptográfia:
http://world.std.com/

\sim

dpj/elliptic.html
http://ds.dial.pipex.com/george.barwood/ec

_

faq.htm

Hraskó András

¹Benedek István és Benedek Marcell fordítása

²Analógiánk annyiban félrevezető, hogy míg az ember megfordulva más tájat lát maga előtt, addig az (1) egyenlet által definiált kúp kettős kúp, az origóra középpontosan tükrös.