Kezdőlap


Cím:	Az 1998/99. évi Arany Dániel Matematikai Tanulóverseny feladatai
Füzet:	1999/november, 457 - 462. oldal	PDF \| MathML
Témakör(ök):	Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

KEZDŐK
Első forduló (Mindhárom kategória)0mm

1. Oldja meg a valós számok halmazán a következő egyenletet!

\begin{matrix} | 1 - | x | | = \frac{1}{2} - x \end{matrix}

2. A

h_{1}

hajó egy folyón

A

-tól

B

-ig lefelé, majd ‐ azonnal visszafordulva ‐

B

-től

A

-ig felfelé a teljes utat

2,5

-szer annyi idő alatt teszi meg, mint a

h_{2}

hajó. Állóvízben a

h_{2}

hajó sebessége a

h_{1}

hajó sebességének kétszerese. Hányszorosa a

h_{1}

hajó állóvízben mért sebessége a folyó sebességének? (A két hajó és a folyó sebessége állandó.)

3. Az

A B C

szabályos háromszög egy belső pontja

P

. Legyen

P

-nek a háromszög

A A_{1}

B B_{1}

C C_{1}

magasságaira eső merőleges vetülete rendre

P_{1}

P_{2}

és

P_{3}

. Bizonyítsa be, hogy az

A P_{1} + B P_{2} + C P_{3}

összeg értéke nem függ a

P

pont megválasztásától!

4. Tekintse a valós számok halmazán értelmezett

\begin{matrix} f (x) : = {(x - 1)}^{4} + {(x - 2)}^{4} + {(x - 3)}^{4} \end{matrix}

függvényt! Hol veszi fel ez a függvény a legkisebb helyettesítési értékét?

5. Mely

n

és

k

pozitív egész számokra teljesül a következő egyenlőség?

\begin{matrix} 3^{n} = 2^{k} + 1 \end{matrix}

Második (döntő) forduló

I. kategória: Szakközépiskolások

1. Határozza meg az

a

b

paraméterek értékét úgy, az alábbi egyenletnek végtelen sok megoldása legyen a valós számok halmazán!

\begin{matrix} | | x - 4 | + 5 - 2 x | = a x + b \end{matrix}

2. Milyen egész

n

esetén lesz az alábbi egyenlet megoldása egész szám?

\begin{matrix} n^{2} (x - 1) = 5 n (2 x - 1) - 25 x \end{matrix}

3. Az

A B C

háromszögben

α = 120^{\circ}

. Az

A

csúcsból induló belső szögfelező a

B C

oldalt

A_{1}

-ben metszi. Legyen

O

A B C

háromszög,

O_{1}

B A_{1} A

háromszög,

O_{2}

C A A_{1}

háromszög köré írt körének középpontja. Bizonyítsa be, hogy az

O O_{1} O_{2}

háromszög szabályos!

II. kategória: Nem speciális matematika tantervű gimnáziumi tanulók

1. Azonos az I. kategória 3. feladatával.

2. Tekintsük az összes kétjegyű pozitív egész számot! Mutassuk meg, hogy ha közülük akárhogyan választunk ki tizenkét darabot, akkor ezek között mindig van két olyan szám, amelyek különbsége azonos számjegyekből álló kétjegyű szám!

3. Egységoldalú szabályos tízszögbe hány darab egységoldalú szabályos ötszöget tudunk úgy elhelyezni, hogy bármely két ötszögnek ne legyen közös belső pontja?

III. kategória: Speciális matematika tantervű gimnáziumi tanulók

1. Legyen

n \geq 3

egész szám! Tekintsünk egy egységoldalú szabályos

2 n

-szöget! Ennek csúcspontjai legyenek a körüljárás sorrendjében:

A_{1}

A_{2}

...

A_{2 n}

. Tekintsük azt a két darab egységoldalú szabályos

n

-szöget, melyek a

2 n

-szög belsejében vannak, és egyik oldaluk

A_{1} A_{2}

, illetve

A_{n} A_{n + 1}

. Bizonyítsuk be, hogy ennek a két szabályos

n

-szögnek van egy közös csúcspontja, viszont több közös pontjuk nincsen!

2. Legyenek

x

y

z

21-nél nem nagyobb pozitív valós számok, amelyek összege 48. Mekkora az

(x + 4) (y + 4) (z + 4)

szorzat legnagyobb és legkisebb értéke?

3. Legyen

f

az egész valós számhalmazon értelmezett olyan függvény, amelyre minden

x

valós számra

f (x + 1) = f (x)

és

f (x + \sqrt[]{2}) = f (x)

. Véges sokszor veszi-e fel az

f

függvény az

f (0)

értéket az

[1; 2]

intervallumon?

HALADÓK
Első forduló

I. kategória: Szakközépiskolai tanulók

1. Az

a

valós paraméter értéke olyan, hogy az

\begin{matrix} \frac{x^{2} - (2 a + 1) x + a^{2} + a}{x^{3} - a^{2} x + a - 1} = 0 \end{matrix}

egyenletnek pontosan egy valós gyöke van.
Oldjuk meg az egyenletet!

2. Az

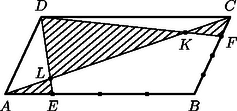
A B C D

paralelogramma

A B

és

B C

oldalát négy egyenlő részre osztjuk. Jelölje a

B C

oldal

C

-hez legközelebbi osztópontját

F

, az

A B

oldal

A

-hoz legközelebbi osztópontját

E

! Kössük össze a pontokat az ábrán látható módon. Hányad része a vonalkázott terület a paralelogramma területének?

3. Oldjuk meg a valós számok körében a

\begin{matrix} \sqrt[]{4 - x} = c + \sqrt[]{x - 1} \end{matrix}

egyenletet, ahol a

c

paraméter értéke egész szám!

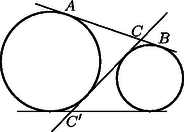
4. Bizonyítsuk be, hogy két kör közös külső érintőszakaszának hossza megegyezik a közös belső érintő egyenesüknek a közös külső érintők közé eső darabjának hosszával (

A B = C C'

5. Legfeljebb hány új egyenes jöhet létre, ha

n

egyenes metszéspontjait összekötjük egymással?

II. kategória: Nem speciális tantervű gimnáziumi tanulók

1. Oldjuk meg a természetes számok (nemnegatív egész számok) halmazán a

\begin{matrix} 3 (x - y) = x^{2} - x y + y^{2} \end{matrix}

egyenletet!

2. Az

A B C D

paralelogramma középpontja

O

és a

D A B

szög egyenlő az

A O D

szöggel. Bizonyítsuk be, hogy ekkor

\begin{matrix} A C^{2} - B D^{2} = 2 (A B^{2} - B C^{2})! \end{matrix}

3. Azonos az előző kategória 3. feladatával.

4. Azonos az előző kategória 4. feladatával.

5. Azonos a az előző kategória 5. feladatával.

III. kategória: Speciális matematika tantervű gimnáziumi tanulók

1. Hány egész számokból álló

(x, y)

számpár elégíti ki a

\begin{matrix} \sqrt[]{2 x - y} = \sqrt[]{x + 2^{1999}} - \sqrt[]{y - x} \end{matrix}

egyenletet?

2. Egy paralelogrammában két szomszédos oldal által és az átlók által bezárt hegyesszög egyenlő nagyságú. Bizonyítsuk be, hogy a rövidebb oldal és a hosszabb oldal aránya nagyobb

(\sqrt[]{2} - 1)

-nél!

3. Bizonyítsuk be, hogy

n > 7

esetén az 1, 2, 3,

...

2 n

számok közül nem lehet

n

darabot úgy kiválasztani, hogy a kiválasztott számokból képzett kéttagú összegek mind különbözők legyenek!

4. Egy tetraéder mindegyik lapja derékszögű háromszög, élei közül pedig három 1 egység hosszú.
a) Hogyan helyezkedhetnek el a derékszögek a csúcsokhoz képest?
b) Mekkora a tetraéder többi éle?

Második forduló

I. kategória: Szakközépiskolai tanulók

1. Oldjuk meg a valós számok körében a

\begin{matrix} \sqrt[]{3 p - x} + \sqrt[]{x - p} = \sqrt[]{p + 2} \end{matrix}

egyenletet, ahol a

p

paraméter egész szám!

2. Egy egyenlő szárú háromszög beírt körének sugara

r

, az alapjához hozzáírt (az alapot és a szárak meghosszabbítását is érintő) kör sugara

r_{a}

, a háromszög köréírt körének sugara pedig

R

.
a) Igazoljuk, hogy

\sqrt[]{r \cdot r_{a}} \leq R

!
b) Mekkora

\frac{r}{R}

értéke, ha

\sqrt[]{r \cdot r_{a}} = R

3. Egy szabályos háromszög oldalait

n

egyenlő részre osztottuk. Legyen

f (n)

azoknak a háromszögeknek a száma, amelyeket az osztópontok és a háromszög csúcsai meghatároznak! Adjuk meg

f (n)

-et

n

függvényeként!

4. Bizonyítsuk be, hogy ha egy tetraéder szemközti élei merőlegesek egymásra, akkor van olyan pont a tetraéder belsejében, amely mindegyik él felezőpontjától egyenlő távolságra van!

II. kategória: Nem speciális tantervű gimnáziumi tanulók

1. Oldjuk meg az egész számok halmazán a

\begin{matrix} \sqrt[]{3 x - y} = \sqrt[]{x + 3} - \sqrt[]{y - x} \end{matrix}

egyenletet!

2. Egy egyenlő szárú háromszög beírt körének sugara

r

, az alapjához hozzáírt (az alapot és a szárak egyenesét is érintő) kör sugara

r_{a}

, a háromszög köréírt körének sugara pedig

R

. Mekkora

\frac{r}{R}

értéke, ha

r + r_{a} = R

3. Egy szabályos háromszög oldalait

n

egyenlő részre osztottuk. Legyen

f (n)

azoknak a háromszögeknek a száma, amelyeket az osztópontok és a háromszög csúcsai meghatároznak! Milyen

n

érték esetén lesz

f (n)

prímszám?

4. Egy kocka alaplapja az

A B C D

négyzet, fedőlapja az

A_{1} B_{1} C_{1} D_{1}

négyzet (

A A_{1}

B B_{1}

C C_{1}

D D_{1}

merőleges a két négyzet síkjára.) Az

A

csúcsra, az

A_{1} B_{1}

él felezőpontjára és a

D D_{1}

él felezőpontjára illeszkedő sík a kockát két részre vágja. Mekkora a keletkezett két test térfogatának aránya?

Harmadik (döntő) forduló

I. kategória: Szakközépiskolások

1. Bizonyítsuk be, hogy ha

x > 0

, akkor

\begin{matrix} \frac{x}{x + 2} + \frac{1}{3 x} + \frac{x}{2 x + 1} \geq 1. \end{matrix}

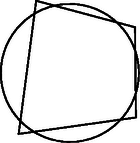
2. Egy kör és egy négyszög úgy helyezkedik el a síkon, mint az az ábrán látható. Tudjuk, hogy a kör négyszögön belüli két-két szembenfekvő ívének összege egyenlő. Bizonyítsuk be, hogy a négyszög húrnégyszög!

3. A 26 és a 65 két olyan kétjegyű szám, hogy ha elhagyjuk a mindkettőben szereplő 6-ost, akkor a kapott két egyjegyű szám hányadosa egyenlő az eredeti két szám hányadosával. Keressük meg az összes különböző kétjegyű számokból álló ilyen tulajdonságú számpárt!

II. kategória: Nem speciális matematika tantervű gimnáziumi tanulók

1. Bizonyítsuk be, hogy ha

x + y > 0

és

\begin{matrix} x^{2} + y^{2} + \frac{2 x y}{x + y} = 1, \end{matrix}

akkor

x + y = 1

2. Bizonyítsuk be, hogy ha egy négyszög csúcsai egy

R

, oldalfelező pontjai pedig egy

r

sugarú körre illeszkednek, akkor a két kör középpontjának távolsága:

\begin{matrix} \sqrt[]{\frac{R^{2}}{2} - r^{2}} . \end{matrix}

3. A

*

művelet a valós számpárokon van értelmezve, az

(x, y)

számpárokhoz rendelt valós számot

x * y

-nal jelöljük. Határozzuk meg

1999 * 19

értékét, ha tudjuk, hogy bármely

x

y

z

valós számra teljesülnek a következő azonosságok:

\begin{matrix} \begin{matrix} x * x & = 0, \\ x * (y * z) & = (x * y) + z . \end{matrix} \end{matrix}

III. kategória: Speciális matematika tantervű gimnáziumi tanulók

1. Egy táblára felírtuk az 1,

p

p^{2}

...

p^{2 n}

számokat, ahol

p

pozitív prímszám,

n

pedig pozitív egész szám. Egy lépésben bármely két szám letörölhető, ha helyükbe a letörölt két szám különbségének abszolút értékét írjuk. Ezt az eljárást addig folytatjuk, amíg egyetlen szám marad a táblán. Jelölje a leírt eljárással kapható számok maximumát

M

, minimumát

m

. Mennyi

p

értéke, ha tudjuk, hogy

M + m

négyzetszám?

2. Oldjuk meg az

x^{3} + y^{3} + 3 x y = 1

egyenletet a valós számpárok körében, ha tudjuk, hogy

x + y > 0

3. Bizonyítsuk be, hogy ha az

A B C

háromszögben

A C B ∢ = 45^{\circ}

, akkor a háromszög lefedhető két,

\frac{A B}{2}

sugarú körlappal!