Cím: Az 1999. évi Nemzetközi Matematikai Diákolimpia feladatainak megoldásai
Füzet: 1999/október, 386 - 394. oldal  PDF  |  MathML 
Témakör(ök): Nemzetközi Matematikai Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A szeptemberi számban közölt beszámoló után most a feladatok megoldása következik lényegében úgy, ahogy azt a szerzők, a magyar csapat tagjai a versenyt követően leírták. Ezúton gratulálunk eredményükhöz, és egyúttal megköszönjük közreműködésüket e cikk elkészítésében.

A szerk.

 
1. Határozzuk meg az összes olyan, legalább három pontot tartalmazó síkbeli véges S ponthalmazt, amire az alábbi feltétel teljesül:
 

S bármely két különböző A, B pontjára az AB szakasz felezőmerőlegese szimmetriatengelye az S halmaznak.

 
Megoldás. Legyen S egy ilyen ponthalmaz. Ekkor legyen az S-ben lévő pontok súlypontja P, és e egy tetszőleges szimmetriatengely. Ha e-re tükrözzük az S ponthalmazt, akkor ugyanehhez a ponthalmazhoz jutunk, tehát ha a súlypontját tükrözzük e-re, akkor önmagába megy át. Ez azt jelenti, hogy P szükségképpen rajta van az e szimmetriatengelyen, azaz a szimmetriatengelyek mind egy ponton mennek át.
Az S halmaz tetszőleges két A, B pontja egyenlő távolságra van P-től, mert P a felező merőlegesükön van. Tehát S pontjai mind ugyanakkora távolságra vannak P-től, azaz egy P körüli körön vannak.
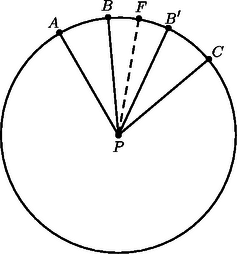
Tegyük fel, hogy A, B, C három S-beli egymás melletti pont a körön ‐ azaz a B-t tartalmazó AC íven a B-n kívül nincs más S-beli pont ‐, amelyekre APB∢<BPC∢. Ekkor legyen az AC ív felezőpontja F. Feltevésünk miatt B az AF íven fog elhelyezkedni, tehát ha az AC szakasz felező merőlegesére tükrözzük (ez éppen a PF egyenes), a tükörkép az FC íven lesz, nevezzük B'-nek. Az AC szakasz felező merőlegese szimmetriatengelye S-nek, tehát B' szükségképpen benne van az S ponthalmazban. Ez viszont ellentmond azon feltevésünknek, hogy A, B, C három egymás melletti pont a körön, mivel B' az FC íven van. Tehát APB∢=BPC∢ tetszőleges egymás melletti pontokra, azaz a szomszédos pontokat összekötő ívek hossza egyenlő, az S pontjai egy szabályos sokszög csúcsai.
Megmutatjuk, hogy a szabályos n-szögek eleget is tesznek a feladat feltételeinek.
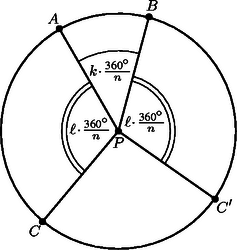
Két egymás melletti Q és R pontra QPR∢=2πn, és két tetszőleges csúcspont és a középpont által meghatározott szög ennek egész számszorosa.
Az A, B, C pontok legyenek S tetszőleges pontjai. Legyen
APB∢=k⋅360∘n,APC∢=ℓ⋅360∘n.
Ekkor AB felezőmerőlegesére tükrözve C-t, C'-höz jutunk,
BPC'∢=APC∢=ℓ⋅360∘n.
Tehát C' szintén pontja a szabályos n-szögnek, mert a BPC'∢ 360∘n többszöröse, és B pontja a szabályos n-szögnek. Tehát az AB szakasz felezőmerőlegesére szimmetrikus lesz a szabályos n-szög.
Tehát ezek az S ponthalmazok éppen a szabályos n-szögek csúcspontjai, ahol n≥3.
  Devecsery András megoldása

 
2. Legyen n egy adott egész szám, amire n≥2.
*(a) Határozzuk meg a legkisebb olyan C konstanst, amire a
∑1≤i<j≤nxixj(xi2+xj2)≤C(∑1≤i≤nxi)4
egyenlőtlenség minden x1,...,xn≥0 valós szám esetén teljesül.
*(b) Határozzuk meg, hogy ezen C konstans mellett mikor áll fenn egyenlőség.
 
Megoldás. Ha xi=0 minden i-re, akkor az egyenlőtlenség 0≤C⋅0, ami minden C mellett teljesül, sőt egyenlőség áll fenn. C meghatározása szempontjából tehát a ∑1≤i≤nxi>0 eset a lényeges, ezt vizsgáljuk tovább. Osszuk el az egyenlőtlenség mindkét oldalát a pozitív (∑1≤i≤nxi)4 számmal:
∑1≤i<j≤nxi∑1≤k≤nxk⋅xj∑1≤k≤nxk((xi∑1≤k≤nxk)2+(xj∑1≤k≤nxk)2)≤C.
Legyen ai=xi∑1≤k≤nxk, így ∑1≤i≤nai=1 és 0≤ai≤1. Az egyenlőtlenség új alakja:
∑1≤i<j≤naiaj(ai2+aj2)≤C.
Becsüljük most meg a bal oldal ai2+aj2 tényezőit felülről ∑1≤k≤nak2-tel:
∑1≤i<j≤naiaj(ai2+aj2)≤∑1≤i<j≤naiaj∑1≤k≤nak2=(∑1≤k≤nak2)(∑1≤i<j≤naiaj).
A második tényezőt ki tudjuk fejezni, mivel
(∑1≤k≤nak)2=∑1≤k≤nak2+2∑1≤i<j≤naiaj,
tehát ∑1≤k≤nak=1 alapján
∑1≤i<j≤naiaj=1-∑1≤k≤nak22.
Legyen M=∑1≤k≤nak2, így
∑1≤i<j≤naiaj(ai2+aj2)≤M1-M2=M-M22=18(1-(2M-1)2)≤18,
mert (2M-1)2≥0.
18-dal az állítás tehát igaz. Kimutatjuk, hogy ez már éles is, tehát C=18. Megnézzük, mikor állhat itt egyenlőség. Pontosan akkor, ha
(2M-1)2=0,azazM=12,valamintaiaj(ai2+aj2)=aiajMminden  i≠j  párra.
Ha lenne három pozitív a szám: ai, aj, ak>0, akkor a második feltétel sérülne, hiszen
aiaj(ai2+aj2)<aiaj(ai2+aj2+ak2)≤aiajM.
Tehát két szám, ai és aj kivételével a többi a szám nulla. Tehát ∑1≤k≤nak=1 miatt ai+aj=1 és ai2+aj2=12 M=12 miatt.
Azaz ai2+(1-ai2)=12, vagyis 4ai2-4ai+2=1, tehát (2ai-1)2=0, tehát ai=12, amiből aj=12.
Ekkor ráadásul a bal oldal értéke éppen 18, tehát C=18.
Ha ai=aj=12, akkor xk=0, ha k≠i, j és xi=xj>0. Azonban xi=0, i=1, 2, ..., n is egyenlőséget eredményez, a (b) részre tehát a válasz:
Egyenlőség akkor és csak akkor áll, ha az x-ek közül n-2 darab 0-val egyenlő, a maradék kettő pedig egymással egyenlő.
  Lukács László megoldása

 
3. Tekintsünk egy n×n-es négyzet alakú táblát, ahol n rögzített páros pozitív egész. A tábla n2 egységnégyzetre van felosztva. Azt mondjuk, hogy a tábla két különböző négyzete szomszédos, ha van egy közös oldaluk.

A táblán N egységnégyzet meg van jelölve olymódon, hogy minden négyzet (jelölt, vagy nem jelölt) szomszédos legalább egy jelölt négyzettel.

Határozzuk meg N lehetséges legkisebb értékét.
 
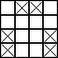
Megoldás. Osszuk be a négyzetet keretekre az ábra szerint, és kívülről kezdve színezzünk minden második keretet feketére. A táblán minden mező pontosan két feketével szomszédos, tehát már ahhoz is meg kell jelölnünk a fekete mezőknek legalább a felét, ha csak annyit akarunk, hogy minden fekete mezőnek legyen megjelölt szomszédja. N tehát legalább ezek számának fele. Számoljuk ezt össze abban az esetben, amikor n 4-gyel is osztható, illetve ha 4-gyel nem osztható (az ábrán a színezés az a) esetnek megfelelő).
4∣n:12[12+(16+12)+...+(n-4416+12)]=12[n412+16n-44⋅n4⋅12]=a)=12[3n+n(n-4)2]=n2+2n4,
4∤n:12[4+(4+16)+...+(4+n-2416)]=12[n+244+16n-24⋅n+24⋅12]=b)=12[n+2+n22-2]=n2+2n4.
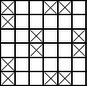
Ezt az értéket viszont el is érhetjük, csak a fekete kereten belül jelölve ki mezőket az alábbi módon: a fekete keretek bal alsó sarkából indulva két szomszédos mezőt kijelölünk, majd kettőt nem, majd kettőt megint igen stb., mindig a keret mentén lépegetve. Így nyilván minden keret felét jelöljük ki, így nyilván összesen n2+2n4 mezőt. A fekete keretek mezőinek nyilván lesz jelölt szomszédja, a fehér keretek mezői mellett pedig van valamelyik szomszédos fekete kereten jelölt mező, hiszen ezek közül a belső jelölését pontosan kettővel ,,feljebb'' kezdtük el, így a két keret jelölt mezői váltogatják egymást.
N lehetséges legkisebb értéke tehát n2+2n4. A jelölést pl. n=2, 4, 6, 8-ra az ábra mutatja.
  Kiss Gergely és Keszegh Balázs*Keszegh Balázs, a budapesti Fazekas Mihály Gyakorló Gimnázium tanulója, a szlovák csapat tagjaként vett részt a versenyen. megoldása alapján

 
Megjegyzés. n=4k+1-re n2+2n+14, n=4k+3-ra n2+2n-34 mezőt kell kijelölni. Ennek bizonyítását itt nem közüljük.

 
4. Határozzuk meg az összes olyan, pozitív egészekből álló (n,p) párt, hogy p prím, n≤2p, és (p-1)n+1 osztható np-1-gyel.
 
Megoldás. Föltehető, hogy n>1, hiszen n=1 tetszőleges p prímmel megoldás. Legyen q az n legkisebb prímosztója, azaz n=qα⋅m, ahol q∤m. q választásából látszik, hogy (q,m)=1, és az is, hogy az m páratlan. Ekkor q∣n∣(p-1)n+1, azaz
(p-1)qα⋅m≡-1(modq).
A kis Fermat-tétel szerint (p-1)q≡p-1(modq). Ennek ismételt alkalmazásával
(p-1)n≡(p-1)m(modq),és így(p-1)m≡-1(modq).(1)
Ebből az is következik, hogy (q,p-1)=1, tehát ismét felhasználva a kis Fermat-tételt
(p-1)q-1≡1(modq).(2)
(1)-et négyzetre emelve
(p-1)2m≡1(modq)(3)
Ha d jelöli q-1 és 2m legnagyobb közös osztóját, akkor az euklideszi algoritmus felhasználásával (2)-ből és (3)-ból (p-1)d≡1(modq) következik.
A d meghatározásához vegyük észre, hogy q választása szerint az m minden prímosztója nagyobb q-nál, így (q-1)-nek és m-nek nincs közös prímosztója. Így d=(q-1,2m) vagy 1, vagy pedig 2. Így mindenképpen (p-1)2≡1(modq).
Ez pontosan akkor teljesül, ha p-1≡1(modq), vagy pedig p-1≡-1(modq).
Az első esetben (1)-ből (p-1)m≡1≡-1(modq), azaz q=2 és így p≡2(modq) miatt p=2. Ekkor a feltételből n=2 következik, és így a p=2, n=2 megoldást kapjuk.
A második esetben p-1≡-1(modq), azaz q∣p, és így q=p>2, n=pα⋅m, a feltételből pedig
pα(p-1)∣(p-1)n+1(4)
következik.
Megmutatjuk, hogy p kitevője (p-1)n+1 prímtényezős felbontásában pontosan α+1. Ebből aztán (4) szerint α(p-1)≤α+1, azaz α⋅(p-2)≤1, tehát α=1 és p=3 adódik.
1+(p-1)n a binomiális tétel szerint (az n páratlan):
1+∑k=0n(-1)n-k(nk)pk=1-1︸0+(n1)p+∑k=2n(-1)n-k⋅(nk)⋅pk.
Az összeg első tagja (n1)p=pα+1⋅m, és tudjuk, hogy p∤m. Azt állítjuk, hogy a további tagok valamennyien oszthatók pα+2-vel, és így 1+(p-1)n=pα+1(m+p⋅K) alakú, és így a második tényező valóban nem osztható p-vel.
Legyen tehát k≥2, és tekintsük a k-adik tagot (n=pα⋅m):
(nk)pk=nk(n-1k-1)⋅pk=pα+k⋅mk(n-1k-1).
Ha p≥3 és k≥2, akkor pk-1>k (ez k-ra vonatkozó indukcióval nyilvánvaló), és így a p prímszám kitevője a k nevezőben legfeljebb k-2. Mivel a pα+k⋅m⋅(n-1k-1) szorzatban csak a k-val való osztás csökkentheti a p kitevőjét, azért ez a kitevő valóban legalább α+k-(k-2)=α+2.
A második esetben tehát arra jutottunk, hogy a p prímszám csak 3 lehet, a feltétel pedig így
n2∣2n+1.

Ismeretes, hogy ez csak az n=1 és n=3 esetben teljesül. Ez volt az 1990. évi pekingi Matematikai Diákolimpia 3. feladata. Megoldása megtalálható Reiman István: Nemzetközi Matematikai Diákolimpiák 1959‐1994 (Typotex Kiadó, Budapest, 1997) című könyvének 442‐444. oldalán.
 
Megjegyzés. Az n≤2p feltétel felhasználásával természetesen nincs szükség erre a hivatkozásra.

  Zábrádi Gergely megoldása

 
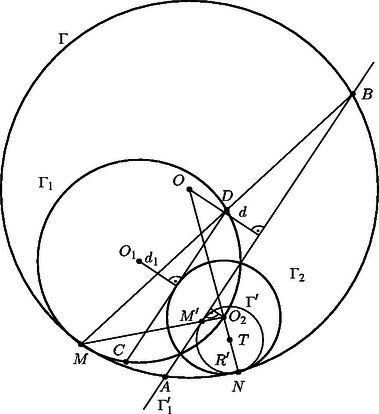
5. A Γ1 és Γ2 körök a Γ kör belsejében vannak és érintik a Γ kört a különböző M, ill. N pontokban.
Γ1 átmegy a Γ2 kör középpontján. A Γ1 és Γ2 körök két metszéspontján átmenő egyenes a Γ kört az A és B pontokban metszi. Az MA és MB egyenesek Γ1-et a C, ill. D pontokban metszik.
Bizonyítsuk be, hogy CD érintője a Γ2 körnek.
 
Megoldás. Először meghatározzuk az O pont AB-től mért d távolságát (a távolságok végig előjelesek). Invertáljunk a Γ2 körre. Γ1 kör képe egyenes, mert átmegy az O2 ponton; ezen az egyenesen vannak Γ1 és Γ2 közös pontjai, így Γ1 képe az AB egyenes. Γ képe érinti Γ1, ill. Γ2 képét, tehát az AB egyenest és a Γ2 kört; AB-t M képében, M'-ben érinti (M' az O2M és AB metszéspontja), Γ2-t N-ben (N képe önmaga), tehát Γ' középpontja, T az ON egyenes metszéspontja az AB-re M'-ben állított merőlegessel. A Γ' kör átmérője, 2R'=R2+R222R-R2=2RR22R-R2 (ha N átellenes pontja Γ-n U, Γ'-n U', akkor az új átmérő hossza NO2+O2U'=R2+R22O2U).
Tehát T távolsága AB-től RR22R-R2.
O2 távolsága az inverzió miatt AB-től R222R1 (ugyanis az O2-ből AB-re bocsátott merőleges talppontja a Γ1 kör O2-vel átellenes pontjának képe lesz.)
O2T=R2-2RR22R-R22=RR2-R222R-R2=R2(R-R2)2R-R2OO2=R-R2OT=2R(R-R2)2R-R2,
tehát
λ=O2TOT=R22R1-λ=OO2OT=2R-R22R.
Ezekből látható, hogy ha O távolsága AB-től d, akkor O2 távolsága AB-től
λ⋅d+(1-λ)⋅TM'=R222R1.

Tehát
d=1λR222R1-1-λλ⋅RR22R-R2=RR2R1-R=R(R2-R1)R1.
Ebből kiszámolhatjuk O1 távolságát CD-től. Γ1 középpontosan hasonló Γ-hoz. A hasonlóság középpontja M, aránya R1R. A Γ-t Γ1-be vivő hasonlóság O-t O1-be, AB-t CD-be viszi, tehát O1 és CD távolsága
d1=R1R⋅d=R2-R1,
ez éppen az igazolandó, mert így O2 távolsága CD-től d1+R1 (AB‖CD miatt), ami nem más, mint R2. Ezzel a bizonyítást befejeztük.
  Gyenes Zoltán megoldása

 
6. Határozzuk meg az összes olyan f:R→R függvényt, amelyre
f(x-f(y))=f(f(y))+xf(y)+f(x)-1
teljesül minden x,y∈R esetén.

 
Megoldás. x helyére f(y)-t helyettesítve és a k=f(0) jelölést használva:
f(0)=f(f(y))+(f(y))2+f(f(y))-1f(f(y))=12(k+1-(f(y))2).
Ezt beírva az eredeti feltételbe:
f(x-f(y))=12(k-1-(f(y))2)+xf(y)+f(x).
Legyen g(x)=f(x)+x22. Ekkor
g(x-f(y))=f(x-f(y))+(x-f(y))22==12(k-1-(f(y))2)+xf(y)+g(x)-x22+(x-f(y))22,g(x-f(y))=xf(y)+g(x)-x22+k-1-(f(y))22-(x-f(y))22=g(x)+k-12.
Először belátjuk, hogy k=1. Mivel az azonosan 0 függvény nem megoldás, létezik olyan y∈R, amelyre f(y)≠0, így x=1f(y)-t helyettesíthetünk az eredeti képletbe:
f(x-f(y))=f(f(y))+f(x),azazf(a)=f(b)+f(c)
alakú egyenlőséget kapunk.
g(x-f(a))=g(x)+k-12,g((x-f(b))-f(c))=g(x-f(b))+k-12=g(x)+k-1.
E kettő egyenlőségéből k-1=k-12, azaz k=1 következik.
Ekkor viszont g(x-f(y))=g(x), tehát f(x) minden x-re periódusa g-nek. Másrészt f(0)=k=1, ebből
f(1)=f(f(0))=12(1+1-1)2=12,
tehát 12 függvényérték, és így g-nek periódusa. De
f(x-1)=f(x-f(0))=f(f(0))+xf(0)+f(x)-1=12+x+f(x)-1=f(x)-12+x
is függvényérték, tehát g-nek periódusa.
Azt kaptuk, hogy g-nek periódusa f(x), f(x-1) és 12, tehát ugyancsak periódus az f(x)-f(x-1)+12, ami pedig éppen x.
Tehát g minden szám szerint periodikus és csak így konstans lehet.
g(0)=f(0)+022=1, tehát g(x)=1, amiből f(x)=1-x22.
Behelyettesítéssel meggyőződhetünk róla, hogy ez valóban megoldás is.
  Terpai Tamás megoldása

 

 

 

 

 

 

 

 
**