Kezdőlap


Cím:	Hogyan fogjunk oroszlánt
Szerző(k):	Kós Géza
Füzet:	1999/február, 76 - 86. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A matematika legkülönfélébb ágaiban előfordulnak olyan tételek, amelyek valamilyen matematikai objektum létezését állítják. Az ilyen tételeket egzisztencia-tételeknek¹ nevezik.
Ebben a cikkben olyan eszközöket vizsgálunk meg, amelyek egzisztencia-tételek bizonyításához használhatóak, leginkább a valós analízis körében.
Először kimondunk néhány tipikus egzisztencia-tételt. Ezek részben szemléltetések, részben pedig eszközök lesznek más egzisztencia-tételek bizonyításához.

Tétel. Létezik olyan pozitív valós szám, amelynek a négyzete

2

A legkisebb felső korlát tétele. Ha a valós számokból álló

H

halmaz felülről korlátos és nem üres, akkor a felső korlátai között van legkisebb.²

Bolzano‐Weierstrass tétel. Tetszőleges korlátos

x_{1}

x_{2}

...

számsorozatnak van torlódási pontja.³

Borel fedési tétele. Ha egy

[a; b]

zárt intervallumot lefedünk akárhány nyílt intervallummal, akkor a nyílt intervallumok közül kiválasztható véges sok, amelyek még mindig lefedik az

[a; b]

intervallumot.

Az algebra alaptétele. Minden legalább elsőfokú, valós vagy komplex együtthatós polinomnak van komplex gyöke.

Ezekben a tételekben közös, hogy egy speciális tulajdonságú szám létezését állítják egy bizonyos halmazban. Egyedül a Borel-tétel látszik kivételnek, de ezt a következőképpen is megfogalmazhatjuk:

Borel fedési tételének átfogalmazása. Ha adott akárhány nyílt intervallum, és ezek közül semelyik véges sok nem fedi le az

[a; b]

intervallumot, akkor létezik olyan

c

szám az

[a; b]

intervallumban, amelyet egyik nyílt intervallum sem tartalmaz.

I. módszer: intervallum-felezés

Ezt a módszert nagyon szemléletesen mutatja be egy klasszikus példázat.
Feladat: Fogjunk a sivatagban oroszlánt. Ehhez rendelkezésünkre áll egy oroszlánjelző műszer, ami a sivatag bármelyik részletéről megállapítja, hogy van-e benne oroszlán.
Megoldás: Két részre osztjuk a sivatagot, és mindkét felét lemérjük a műszerrel. Ha az egész sivatagban van oroszlán, akkor legalább az egyik felében szintén van. Kiválasztjuk az egyik ilyen fél sivatagot, a másik felét eldobjuk. A fél sivatagot ismét két részre osztjuk; az egyik részt (amiben van oroszlán) megtartjuk, a másik részt ismét eldobjuk. A felezgetést akkor hagyjuk abba, amikor a megmaradt sivatag darab már elég kicsi (azaz csupán egyetlen homokszemből áll), és akkor ráborítunk egy ketrecet. Ezzel megfogtuk az oroszlánt.
A gyakorlatban az oroszlán az a matematikai objektum, aminek a létezését bizonyítani akarjuk, például egy speciális tulajdonságú szám. A sivatag az a halmaz, amelynek elemei között keressük a kérdéses objektumot, legtöbbször egy intervallum. Az intervallumot természetesen nem elég véges sokszor két részre osztani. Végtelen sok felezésre van szükség, hogy végül csak egyetlen szám maradjon.
Sajnos a ,,megoldásban'' komoly hiányosságok vannak. Ahhoz, hogy kijelenthessük: megfogtuk az oroszlánt, a következő három kérdést kell tisztáznunk:

*	K1. Biztosak lehetünk-e abban, hogy egyáltalán fogtunk valamit?

*	K2. Csak egyvalamit fogtunk?

*	K3. Hogyan győződhetünk meg róla, hogy oroszlánt fogtunk, és nem valami mást?

Ezeknek a kérdéseknek a megválaszolása nélkül a ,,megoldás'' utolsó mondata közönséges blöff.
Tanulságképpen nézzük meg, mire jutottak volna az ókori görögök a

\sqrt[]{2}

-vel.

Akhilleusz és a

\sqrt[]{2}

Az ókori görögök csak a racionális számokat ismerték, és tragikus felismerés volt számukra, hogy nincs olyan (racionális) szám, aminek a négyzete

2

, holott a geometriában meg tudtak szerkeszteni ilyen hosszúságú szakaszt.
Képzeljük el, hogy Akhilleusz, a mesebeli görög hős megpróbálja megtalálni azt a számot, amelynek négyzete

2

. Akhilleusz úgy találja, hogy az

1

túl kicsi (a négyzete kisebb, mint 2), a

2

viszont túl nagy. Ezért úgy dönt, hogy a számot az

(1; 2)

intervallumban keresi.
Ezután kipróbálja a

\frac{3}{2}

számot, és megállapítja, hogy ez is túl nagy, mert a négyzete

\frac{9}{4}

, ami nagyobb

2

-nél. Ezért a

\frac{3}{2}

-t és a nála nagyobb számokat eldobja, és csak az

(1; \frac{3}{2})

intervallummal foglalkozik tovább. Ezután az

\frac{5}{4}

számot próbálja ki (túl kicsi), majd a

\frac{11}{8}

-ot (túl kicsi), és így tovább. Közben az intervallum, amelyben a

\sqrt[]{2}

-t keresi, egyre fogy:

\begin{matrix} (1; 2), (1; \frac{3}{2}), (\frac{5}{4}; \frac{3}{2}), (\frac{11}{8}; \frac{3}{2}), (\frac{11}{8}; \frac{23}{16}), (\frac{43}{32}; \frac{23}{16}), ... . \end{matrix}

Akhilleusznak elég sok ideje van, és az intervallum-felező lépést végtelen sokszor elvégzi. Közben kidobja az összes olyan racionális számot, aminek a négyzete nagyobb

2

-nél, és azokat is, amelyeknek a négyzete kisebb

2

-nél.
Ekkor kellemetlen meglepetés éri: az összes racionális számot kidobta, nem maradt egy sem.

A valós számok axiómarendszere

Akhilleusz problémáján úgy lehet segíteni, hogy a racionális számokon kívül további számokat vezetünk be. Az nyilván kevés, ha csak egy új számot (a

\sqrt[]{2}

-t) találunk ki, szükség van még

\sqrt[]{3}

-ra,

\sqrt[11]{7}

-re, az

1,01001000100001 ... .

tizedes törtre és még rengeteg más számra. Az új számokkal mit is akarnánk mást, mint számolni, tehát a jól megszokott alapműveleteket és a rendezést (a kisebb-nagyobb relációt) ki akarjuk terjeszteni az ,,új'' számokra is.
A racionális számok kiegészítésére több konstrukció is létezik. Vannak természetesnek nevezhető konstrukciók, például mondhatjuk azt, hogy ezentúl a végtelen tizedes törteket nevezzük számoknak. Ennek a konstrukciónak az a hátránya, hogy a műveleteket ‐ különösen a szorzást ‐ nagyon nehéz definiálni. Vannak kevésbé természetes konstrukciók, amelyek nem annyira szemléletesek, de lényegesen könnyebb a műveleteket definiálni; ilyenek például a racionális számok Dedekind-szeletei⁴ vagy a racionális számokból készített Cauchy-sorozatok ekvivalencia-osztályai.⁵
Magukat az új számokat ,,valós'' (azaz létező) számoknak fogjuk hívni. Most nem az a célunk, hogy a lehetséges konstrukciókat tanulmányozzuk, vagy hogy az egyik konstrukciót előnyben részesítsük a többivel szemben. Inkább nem mondjuk meg, hogy milyen objektumokat nevezünk valós számnak, hanem csak a legfontosabb tulajdonságaikat soroljuk fel. Ezeket a tulajdonságokat hívjuk a valós számok axiómáinak.
Az axiómákat négy csoportra oszthatjuk:
I. Testaxiómák. Létezik két kétváltozós művelet, az összeadás és a szorzás, valamint két különböző kitüntetett szám, a

0

és az

1

a következő tulajdonságokkal:

*	T1. Tetszőleges $a$ , $b$ valós számokra $a + b = b + a$ .

*	T2. Tetszőleges $a$ , $b$ , $c$ valós számokra $(a + b) + c = a + (b + c)$ .

*	T3. Tetszőleges $a$ valós számra $a + 0 = a$ .

*	T4. Tetszőleges $a$ valós számhoz létezik olyan $b$ valós szám, amelyre $a + b = 0$ .

*	T5. Tetszőleges $a$ , $b$ valós számokra $a \cdot b = b \cdot a$ .

*	T6. Tetszőleges $a$ , $b$ , $c$ valós számokra $(a \cdot b) \cdot c = a \cdot (b \cdot c)$ .

*	T7. Tetszőleges $a$ valós számra $a \cdot 1 = a$ .

*	T8. Tetszőleges $0$ -tól különböző $a$ valós számhoz létezik olyan $b$ valós szám, amelyre $a \cdot b = 1$ .

*	T9. Tetszőleges $a$ , $b$ , $c$ valós számokra $(a + b) \cdot c = (a \cdot c) + (b \cdot c)$ .

Általában, egy algebrai struktúrát testnek nevezünk, ha teljesülnek ezek az axiómák. Testet alkotnak például a

0

1

2

számok, ha az összeadást és a szorzást modulo

3

végezzük (pl.

2 + 2 = 1

), vagy például a racionális törtfüggvények.
A testaxiómákból bebizonyítható az összes jól ismert műveleti azonosság, és sok más fontos tétel, például az, hogy egy polinomból ki lehet emelni a gyöktényezőket.
II. Rendezési axiómák: Létezik egy

<

reláció a következő tulajdonságokkal:

*	R1. Tetszőleges $a$ , $b$ számokra vagy $a = b$ , vagy $a < b$ , vagy $b < a$ .

*	R2. Ha az $a$ , $b$ , $c$ számokra $a < b$ és $b < c$ , akkor $a < c$ .

*	R3. Ha az $a$ , $b$ , $c$ számokra $a < b$ , akkor $a + c < b + c$ .

*	R4. Ha az $a$ , $b$ , $c$ számokra $a < b$ és $0 < c$ , akkor $a \cdot c < b \cdot c$ .

Egy struktúrát rendezett testnek hívunk, ha teljesülnek rá a test- és rendezési axiómák.
Érdekesség, hogy nem mondtuk ki, hogy

0 < 1

; ezt az axiómákból be lehet bizonyítani.
Ezek után definiálhatjuk a pozitív egész számokat:

1

1 + 1

1 + 1 + 1

stb. A rendezési axiómák garantálják többek között azt is, hogy ezek a számok különbözőek.
III. Arkhimédészi axióma: Tetszőleges valós számnál van nagyobb pozitív egész szám.
Ez az állítás nem következik a korábbiakból. Például a racionális törtfüggvények között lehet definiálni egy

<

relációt úgy, hogy rendezett testet alkossanak, de ne teljesüljön az Arkhimédészi axióma.
IV. Cantor-axióma: Egymásba skatulyázott zárt intervallumok sorozatának mindig van közös pontja. Más szóval, ha adott két számsorozat:

a_{1} \leq a_{2} \leq ...

és

b_{1} \geq b_{2} \geq ...

úgy, hogy tetszőleges

n

-re

a_{n} \leq b_{n}

, akkor az

[a_{1}; b_{1}] \supset [a_{2}; b_{2}] \supset [a_{3}; b_{3}] \supset ...

intervallumoknak van közös eleme.
Az Arkhimédészi és a Cantor-axióma megadja a választ a K1 és K2 kérdésekre. Tegyük fel, hogy az

[a_{0}; b_{0}]

intervallumból indultunk ki. Az intervallum felosztásakor a felezőpontot ne dobjuk ki; ezáltal egy zárt intervallumokból álló

[a_{0}; b_{0}] \supset [a_{1}; b_{1}] \supset [a_{2}; b_{2}] \supset ...

sorozatot kapunk, amelyben az

n

-edik intervallum hossza

b_{n} - a_{n} = \frac{b_{0} - a_{0}}{2^{n}}

. Ezeknek az intervallumoknak a Cantor-axióma szerint van közös eleme.
Ha az intervallumoknak legalább két közös eleme van:

c

és

d

, ahol

c < d

, akkor minden

n

-re

[c; d] \subset [a_{n}; b_{n}]

teljesül. Ebből következik, hogy

d - c \leq b_{n} - a_{n} = \frac{b_{0} - a_{0}}{2^{n}}

, azaz

2^{n} < \frac{b_{0} - a_{0}}{d - c}

. Ez azonban azt jelenti, hogy a

\frac{b_{0} - a_{0}}{d - c}

szám minden

2

-hatványnál ‐ és ezáltal minden pozitív egésznél ‐ nagyobb, ami ellentmond az Arkhimédészi axiómának. Tehát a K1 és a K2 kérdésekre igen a válasz.

Első bizonyítás a

\sqrt[]{2}

létezésére

Most már minden szükséges eszköz rendelkezésünkre áll, hogy bebizonyítsuk a

\sqrt[]{2}

létezését.
Akhilleuszhoz hasonlóan definiálunk egy intervallumsorozatot. Legyen

[a_{0}; b_{0}] = [1; 2]

. Ha

[a_{n}; b_{n}]

-et már definiáltuk, akkor vizsgáljuk meg, hogy

{(\frac{a_{n} + b_{n}}{2})}^{2}

nagyobb-e mint

2

. Ha

{(\frac{a_{n} + b_{n}}{2})}^{2} > 2

, akkor legyen

[a_{n + 1}; b_{n + 1}] = [a_{n}; \frac{a_{n} + b_{n}}{2}]

. Ellenkező esetben legyen

[a_{n + 1}; b_{n + 1}] = [\frac{a_{n} + b_{n}}{2}; b_{n}]

. Ezzel egy olyan

\begin{matrix} [a_{0}; b_{0}] \supset [a_{1}; b_{1}] \supset [a_{2}; b_{2}] \supset ... \end{matrix}

intervallum-sorozatot definiáltunk, amelyben tetszőleges

n

-re

a_{n}^{2} \leq 2

és

b_{n}^{2} \geq 2

.
Az intervallumsorozatnak létezik egyetlen közös eleme; jelöljük ezt

c

-vel. Már csak azt kell bebizonyítanunk, hogy a K3 kérdés szavaival

c

egy oroszlán, azaz

c^{2} = 2

.
Tetszőleges

n

-re igaz, hogy

c^{2} \leq b_{n}^{2}

és

a_{n}^{2} \leq 2

, ezért

\begin{matrix} c^{2} - 2 \leq b_{n}^{2} - a_{n}^{2} = (b_{n} - a_{n}) (b_{n} + a_{n}) < \frac{1}{2^{n}} \cdot (2 + 2) = \frac{4}{2^{n}} . \end{matrix}

Ha a

c^{2} \geq a_{n}^{2}

és

b_{n}^{2} \geq 2

egyenlőtlenségből indulunk ki, akkor pontosan ugyanezt kapjuk

(2 - c^{2})

-re. A két eredmény együtt azt állítja, hogy

\begin{matrix} | c^{2} - 2 | < \frac{4}{2^{n}} . \end{matrix}

Az Arkhimédészi axióma miatt a

\frac{4}{2^{n}}

szám tetszőleges pozitív számnál kisebb lesz, ha

n

elég nagy, ezért

| c^{2} - 2 |

nem lehet pozitív.

| c^{2} - 2 |

tehát

0

, azaz

c^{2} = 2

A legkisebb felső korlát tétele

Ugyanezzel a módszerrel bizonyíthatjuk be a legkisebb felső korlát tételét.
Legyen

L_{0}

egy olyan szám, amely nem felső korlátja

H

-nak (Ilyen létezik, mert

H

nem üres), és legyen

K_{0}

egy felső korlát. A

K_{0}

-nál nagyobb számok is mind felső korlátok, ezért biztosan

L_{0} < K_{0}

.
A legkisebb felső korlátot nyilván a

[L_{0}; K_{0}]

intervallumban érdemes keresnünk. Ezt az intervallumot fogjuk felezgetni.
Ha már definiáltuk az

[L_{n}; K_{n}]

intervallumot, akkor vizsgáljuk meg, hogy

\frac{L_{n} + K_{n}}{2}

felső korlátja-e

H

-nak. Ha igen, akkor legyen

[L_{n + 1}; K_{n + 1}] = [L_{n}; \frac{L_{n} + K_{n}}{2}]

. Ha

\frac{L_{n} + K_{n}}{2}

nem felső korlát, akkor legyen

[L_{n + 1}; K_{n + 1}] = [\frac{L_{n} + K_{n}}{2}; K_{n}]

.
Az így definiált

\begin{matrix} [L_{0}; K_{0}] \supset [L_{1}; K_{1}] \supset [L_{2}; K_{2}] \supset ... \end{matrix}

intervallumsorozatban tetszőleges

n

-re

K_{n}

felső korlátja a

H

halmaznak,

L_{n}

pedig nem felső korlátja.
Az intervallumoknak létezik pontosan egy közös eleme, legyen ez

M

. Azt kell bebizonyítanunk, hogy

M

felső korlátja

H

-nak, és nincs

M

-nél kisebb felső korlát.
Legyen

h

H

halmaz egy tetszőleges eleme. Bármely

n

pozitív egészre

K_{n}

felső korlát, ezért

h \leq K_{n}

; másrészt

M \geq L_{n}

. Ebből következik, hogy

\begin{matrix} h - M \leq K_{n} - L_{n} = \frac{K_{0} - L_{0}}{2^{n}} . \end{matrix}

Ebből az Arkhimédészi axióma miatt következik, hogy

h - M

nem lehet pozitív, vagyis

h \leq M

. Ezzel igazoltuk, hogy

M

felső korlát.
Legyen

K

egy tetszőleges felső korlátja

H

-nak. Ekkor tetszőleges

n

esetén

M \leq K_{n}

a konstrukció miatt és

L_{n} < K

, mert a

K

-nál nem kisebb számok mind felső korlátok; ezért

\begin{matrix} M - K < K_{n} - L_{n} = \frac{K_{0} - L_{0}}{2^{n}} . \end{matrix}

Ebből következik, hogy

M - K

nem lehet pozitív, azaz

M \leq K

. Az

M

számnál tehát nincs kisebb felső korlát.
A legkisebb felső korlátot latin eredetű kifejezéssel szuprémumnak is nevezzük, a

H

halmaz szuprémumát (legkisebb felső korlátját)

{sup}_{}^{} H

-val jelöljük. A tétel párja a legnagyobb alsó korlát tétele: Tetszőleges nem üres, alulról korlátos halmaznak létezik legnagyobb alsó korlátja. Ezt infimumnak is nevezzük, jele

{inf}_{}^{} H

.
Ha a halmaznak létezik legnagyobb, illetve legkisebb eleme (maximuma, illetve minimuma), akkor ez természetesen azonos a halmaz szuprémumával, illetve infimumával. Maximuma és minimuma nincs minden halmaznak, viszont szuprémuma és infimuma minden nem üres és korlátos halmaznak van.
Érdekesség, hogy a valós számok axiómarendszerében az Arkhimédészi és a Cantor-axióma helyett a legkisebb felső korlát tételét is kimondhatjuk axiómaként. A test- és rendezési axiómákból, valamint a legkisebb felső korlát tételéből nagyon könnyű bebizonyítani a Cantor- és az Arkhimédészi axiómát.
Túl ezen, a legkisebb felső korlát tétele egy másik nagyon fontos eszköz egzisztencia-tételek bizonyítására.

II. módszer: a legkisebb felső korlát tételének alkalmazása

Egy autóút mentén a bokrok között oroszlánok bújtak el (legalább egy). Feladat: fogjunk meg legalább egy oroszlánt. Ismét rendelkezésünkre áll egy műszer, amely az autóút bármely szakaszára meg tudja mondani, hogy van-e ott oroszlán.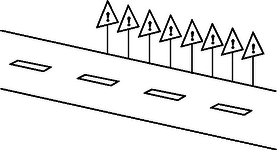

1. ábra

Megoldás: Minden egyes pontban állapítsuk meg, hogy az út hátralevő részén van-e oroszlán. Ha van, tegyünk ki egy ,,Oroszlánveszély'' feliratú táblát. Ahol a táblák elfogynak, ott bújt el egy oroszlán.
Tegyük fel, hogy egy

[a; b]

intervallumban keresünk egy bizonyos

c

számot, és az intervallum bármelyik eleméről valamilyen módszerrel meg tudjuk állapítani, hogy a keresett

c

-nél kisebb vagy nagyobb. A

c

-nél nem nagyobb számok azok a helyek, ahova ,,táblát teszünk''; ezeket a számokat összegyűjtjük egy

T

halmazban. Az a hely, ahol ,,a táblák elfogynak'', a

T

halmaz szuprémuma.
A szuprémum egyértelműen létezik, viszont ismét meg kell vizsgálnunk, hogy oroszlán-e, azaz rendelkezik-e a kívánt tulajdonságokkal.
A továbbiakban a két módszer alkalmazásaként bebizonyítjuk a bevezetőben kimondott tételeket.

Második bizonyítás a

\sqrt[]{2}

létezésére

\sqrt[]{2}

-t ismét az

[1, 2]

intervallumban keressük. Azok a számok nem nagyobbak

\sqrt[]{2}

-nél, amelyek négyzete nem nagyobb

2

-nél, ezért legyen

\begin{matrix} T = {t \in [1, 2] : t^{2} \leq 2} \end{matrix}

és

c = {sup}_{}^{} T

. A

T

halmaz nem üres, mert például

1 \in T

. Ugyanakkor felülről korlátos, például a

2

egy felső korlátja. Ezért a

c

szám definíciója értelmes.
Azt akarjuk igazolni, hogy

c^{2} = 2

.
Tetszőleges

0 < ε < 1

esetén

c - ε

nem felső korlátja

T

-nek, (

c

a legkisebb felső korlát), ezért létezik olyan

t \in T

elem, amelyre

c - ε < t \leq c

. Felhasználva, hogy

t \in T

esetén

t^{2} \leq 2

\begin{matrix} c^{2} - 2 \leq c^{2} - t^{2} = (c - t) (c + t) < ε \cdot (2 + 2) = 4 ε . \end{matrix}

Hasonlóképpen, mivel

c

a legkisebb felső korlát,

c + ε

nem eleme a

T

halmaznak, ezért

{(c + ε)}^{2} > 2

, amiből következik, hogy

\begin{matrix} 2 - c^{2} < {(c + ε)}^{2} - c^{2} = 2 c ε + ε^{2} < 5 ε . \end{matrix}

Azt kaptuk, hogy tetszőleges

0 < ε < 1

esetén

| c^{2} - 2 | < 5 ε

. Ez pedig csak úgy lehetséges, ha

| c^{2} - 2 |

nem pozitív, azaz

c^{2} = 2

A Bolzano‐Weierstrass tétel bizonyítása intervallum-felezéssel

Definiálunk egy olyan

[a_{0}; b_{0}] \supset [a_{1}; b_{1}] \supset [a_{2}; b_{2}] \supset ...

intervallum-sorozatot, amelyre tetszőleges

n

esetén

[a_{n}; b_{n}]

x_{1}

x_{2}

...

sorozatnak végtelen sok elemét tartalmazza.
Legyen

[a_{0}; b_{0}]

egy olyan intervallum, amely a teljes

x_{1}

x_{2}

...

sorozatot tartalmazza.
Ha az

[a_{n}; b_{n}]

intervallumot már definiáltuk, és az végtelen sok elemet tartalmaz az

x_{1}

x_{2}

...

sorozatból, akkor az

[a_{n}; \frac{a_{n} + b_{n}}{2}]

és

[\frac{a_{n} + b_{n}}{2}; b_{n}]

intervallumok közül legalább az egyik szintén végtelen sok elemet tartalmaz. Az egyik ilyet válasszuk

[a_{n + 1}; b_{n + 1}]

-nek.
A

[a_{n}; b_{n}]

intervallumoknak létezik egy közös

c

eleme. Azt állítjuk, hogy ez torlódási pont. Tetszőleges

ε > 0

esetén létezik egy olyan

n

szám, amelyre

[a_{n}; b_{n}] \subset (c - ε; c + ε)

. Az

[a_{n}; b_{n}]

intervallum végtelen sok elemet tartalmaz az

x_{1}

x_{2}

...

sorozatból; ezeket a

(c - ε; c + ε)

intervallum is tartalmazza.

A Bolzano‐Weierstrass tétel bizonyítása a legkisebb felső korlát tételével

Legyen az

x_{1}

x_{2}

...

sorozat egy alsó, illetve felső korlátja

A

, illetve

B

. Legyen

T

azoknak a

t

valós számoknak a halmaza, amelyekre a

[t; B]

intervallum végtelen sok elemet tartalmaz az

x_{1}

x_{2}

...

sorozatból. Ez a halmaz nem üres, például

A \in T

, és felülről korlátos, például

B

egy felső korlátja. Létezik tehát legkisebb felső korlátja; legyen ez

c

.
Tetszőleges

ε > 0

esetén

c + ε

nem eleme a

T

halmaznak (nagyobb

c

-nél, a felső korlátnál), ezért a

[c + ε; B]

intervallum csak véges sok elemet tartalmaz az

x_{1}

x_{2}

...

sorozatból.
A

c - ε

szám viszont nem felső korlát (kisebb

c

-nél, a legkisebb felső korlátnál), ezért létezik egy olyan

t > c - ε

szám, ami eleme

T

-nek. Ez azt jelenti, hogy a

[t; B] \subset (c - ε; B]

intervallum végtelen sok elemet tartalmaz az

x_{1}

x_{2}

...

sorozatból.
Összefoglalva, tetszőleges

ε

esetén a

(c - ε; B]

intervallum végtelen sok, a

[c + ε; B]

intervallum viszont csak véges sok elemet tartalmaz az

x_{1}

x_{2}

...

sorozatból; ebből következik, hogy a két intervallum különbsége,

(c - ε; c + ε)

is végtelen sokat tartalmaz.

Borel fedési tételének bizonyítása intervallum-felezéssel

Tegyük fel, hogy az

[a, b]

intervallumot nem lehet lefedni véges sok nyílt intervallummal. Definiálunk egy olyan

[a_{0}; b_{0}] \supset [a_{1}; b_{1}] \supset [a_{2}; b_{2}] \supset ...

intervallum-sorozatot, amelyre tetszőleges

n

esetén az

[a_{n}; b_{n}]

intervallum nem fedhető le véges sok nyílt intervallummal.
Legyen

[a_{0}; b_{0}] = [a; b]

. Ha már definiáltuk

[a_{n}; b_{n}]

-et és ez nem fedhető le véges sok nyílt intervallummal, akkor az

[a_{n}; \frac{a_{n} + b_{n}}{2}]

és

[\frac{a_{n} + b_{n}}{2}; b_{n}]

intervallumok közül legalább az egyiket szintén nem lehet véges sok nyílt intervallummal lefedni. Az egyik ilyet válasszuk

[a_{n + 1}; b_{n + 1}]

-nek.
A

[a_{n}; b_{n}]

intervallumoknak létezik egy közös

c

eleme. Tegyük fel, hogy

c

eleme egy

I

nyílt intervallumnak. Ekkor elég nagy

n

esetén

[a_{n}; b_{n}] \subset I

. Ez viszont ellentmondás, mert

I

egymagában lefedi az

[a_{n}; b_{n}]

intervallumot. A

c

számot tehát egyik nyílt intervallum sem tartalmazza.

Borel fedési tételének bizonyítása a legkisebb felső korlát tételével

Tegyük fel ismét, hogy az

[a, b]

intervallumot nem lehet lefedni véges sok nyílt intervallummal. Legyen

T

azoknak a

[a; b]

-beli

t

számoknak a halmaza, amelyekre a

[t; b]

intervallum nem fedhető le véges sok nyílt intervallummal. A

T

halmaz nem üres, például

a \in T

, másrészt felülről korlátos. Legyen

c = {sup}_{}^{} T

.
Ha

c

-t egyik nyílt intervallum sem tartalmazza, kész vagyunk. Tegyük tehát fel, hogy

c

-t tartalmazza egy

(u, v)

nyílt intervallum. Ekkor

c < v

miatt

v

nem eleme

T

-nek, és a

[c; b]

intervallum lefedhető véges sok nyílt intervallummal. Ezek

(u, v)

-vel együtt az

(u; b]

intervallumot is lefedik. Tehát tetszőleges

t > u

esetén a

[t; b]

intervallum lefedhető véges sok nyílt intervallummal. Ebből következik, hogy

u

is felső korlátja

T

-nek, ami ellentmond annak, hogy

c

a legkisebb felső korlát.

Az algebra alaptétele

Az algebra alaptételét csak vázlatosan bizonyítjuk. A korrekt bizonyításhoz szükség lenne több fogalom pontos definiálására, amelyek a bizonyítást sokkal hosszabbra nyújtanák.
Tekintsük a

\begin{matrix} p (z) = a_{k} z^{k} + a_{k - 1} z^{k - 1} + ... + a_{1} z + a_{0} \end{matrix}

polinomot, ahol

k \geq 1

és

a_{k} \neq 0

, és tegyük fel indirekte, hogy nincs gyöke a komplex számok körében.
A polinomot mint a komplex számokon értelmezett komplex értékű függvényt ábrázoljuk úgy, hogy a komplex számsík minden pontjába rajzoljuk be a polinom itteni helyettesítési értékét. Így minden egyes pontba egy vektort rajzoltunk.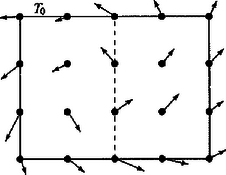

2. ábra

A komplex síkon egy függvénynek tetszőleges téglalapon definiálhatjuk a körülfordulási számát. Ez azt mondja meg, hogy a téglalap kerületén pozitív irányban körbehaladva a függvényértékek összesen hányszor fordulnak körbe. A körülfordulási számot ,,előjelesen'' számítjuk. Ha például a függvényértékek előbb

60^{\circ}

-ot fordulnak pozitív irányba, majd

420^{\circ}

-ot negatív irányba, akkor összesen

360^{\circ}

-ot fordulnak negatív irányba, és a körülfordulási szám

- 1

.
Tekintsünk egy

T_{0}

téglalapot, amely a belsejében tartalmazza a

0

-t. Ha az

a_{k} z^{k}

függvényt ábrázoljuk, akkor a komplex hatványozás tulajdonságai miatt a körüljárási szám pontosan

k

.
Válasszuk a téglalapot olyan nagyra, hogy kerületén az

a_{k} z^{k}

tag sokkal nagyobb legyen, mint az összes többi tag együttvéve. Ekkor a téglalap kerületén a függvényértékek iránya majdnem ugyanaz lesz, mint az

a_{k} z^{k}

iránya, és a körüljárási szám nem változik.
Felezzük el a téglalapot valamelyik oldalával párhuzamosan. Ha körbesétálunk a két fél téglalap kerületén, akkor az egész téglalap kerületének minden szakaszán pontosan egyszer haladunk végig, a két fél téglalap közötti szakaszon pedig mindkét irányban pontosan egyszer. Emiatt a két fél téglalapon a körüljárási számok összege megegyezik a teljes téglalap körüljárási számával.
Most definiáljuk a

T_{0} \supset T_{1} \supset T_{2} \supset ...

téglalapokat úgy, hogy tetszőleges

n

pozitív egész esetén

p

körüljárási száma a

T_{n}

téglalapon pozitív legyen. A

T_{0}

téglalapot már definiáltuk. Ha

T_{n}

-et már előállítottuk, akkor felezzük el a hosszabbik oldalára merőlegesen. Ezzel két fél téglalapra bontottuk. A két fél téglalapon a körüljárási számok összege megegyezik

T_{n}

körüljárási számával, ami pozitív. Ebből következik, hogy legalább az egyik fél téglalap körüljárási száma pozitív. Az egyik ilyen fél téglalapot válasszuk

T_{n + 1}

-nek.
Nem nehéz meggondolni, hogy a téglalapoknak egyetlen közös pontja van. Legyen ez

c

. Azt állítjuk, hogy

c

gyöke a polinomnak.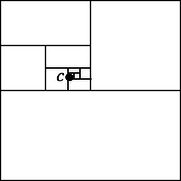

3. ábra

4. ábra

Tegyük fel, hogy

c

nem gyök, azaz

p (c) \neq 0

. Mivel a polinom folytonos, rajzolhatunk

c

körül egy elég kis kört úgy, hogy annak belsejében a polinom értékének iránya

p (c)

irányától legfeljebb

90^{\circ}

-kal térjen el. Ez a kör tartalmazza a

T_{n}

téglalapot, ha

n

elég nagy. Ez viszont ellentmondás, mert a körüljárási szám

T_{n}

-en pozitív, ugyanakkor a kör belsejében a függvényértékek egy félsíkba esnek, egyszer sem tudnak tehát körbefordulni.

,,Oroszlánfogás'' a Téli Ankéton

Feladatok

1. Bizonyítsuk be mindkét módszerrel Bolzano tételét: Ha

f

[a; b]

intervallumon értelmezett folytonos függvény,

f (a) < 0

és

f (b) > 0

, akkor létezik olyan

c \in (a; b)

szám, amelyre

f (c) = 0

2. Bizonyítsuk be mindkét módszerrel Weierstrass tételét: Tetszőleges, az

[a; b]

intervallumon értelmezett folytonos

f

függvénynek létezik maximuma és minimuma. (Segítség: Keressünk olyan

c

számot, amelyre

f (c)

f

értékkészletének szuprémuma, illetve infimuma.)

3. Keressünk a valós számok axiómái között olyat, amelyik következik a többiből.

4. Igaz marad-e a Cantor-axióma, ha zárt intervallumok helyett nyílt intervallumokkal mondjuk ki?

5. Miért nincs legkisebb felső korlátja az üres halmaznak?

6. Bizonyítsuk be a test- és rendezési axiómákból valamint a legkisebb felső korlát tételéből az Arkhimédészi és a Cantor-axiómát.

7. Mutassunk példát olyan rendezett testre, amelyben teljesül a Cantor-axióma, de nem teljesül az Arkhimédészi axióma.

8. Adjunk meg olyan rendezést a racionális törtfüggvények testén, hogy rendezett testet alkossanak és ne teljesüljön az Arkhimédészi axióma.

9. Egy

p

polinomnak nincs gyöke a

T

téglalap kerületén, ahol a körüljárási száma

n

. Bizonyítsuk be, hogy a polinomnak, az esetleges többszörös gyököket multiplicitással számolva, pontosan

n

gyöke van a téglalap belsejében.

Kós Géza

¹A latin egzisztencia szó jelentése: létezés

²A $H$ halmaznak a $K$ szám felső korlátja, ha $H$ -nak nincs $K$ -nál nagyobb eleme. Egy halmaz felülről korlátos, ha létezik felső korlátja.

³Egy sorozatnak a $c$ szám torlódási pontja, ha tetszőleges pozitív $ε$ esetén a sorozatnak végtelen sok eleme esik a $(c - ε; c + ε)$ intervallumba.

⁴A $H \subset Q$ halmazt a racionális számok Dedekind-szeletének hívjuk, ha tetszőleges $q_{1} < q_{2}$ racionális számokra $q_{2} \in H$ esetén $q_{1} \in H$ . Egy ilyen szelet megfelel annak, hogy a racionális számok halmazát egy valós számnál ,,elvágjuk''.

⁵A $q_{1}$ , $q_{2}$ , $...$ sorozatot Cauchy-sorozatnak hívjuk, ha tetszőleges $ε > 0$ -hoz létezik olyan $n_{0}$ pozitív egész, hogy tetszőleges $m, n > n_{0}$ esetén $| q_{n} - q_{m} | < ε .$ A $q_{1}$ , $q_{2}$ , $...$ és $r_{1}$ , $r_{2}$ , $...$ Cauchy-sorozatokat ekvivalensnek nevezzük, ha $(q_{n} - r_{n}) \to 0$ .