Cím:	1998. évi Kürschák József Matemaikai Tanulóverseny feladatainak megoldása
Szerző(k):	Károlyi Gyula
Füzet:	1999/február, 70 - 74. oldal	PDF  |  MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd)

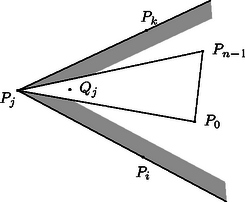
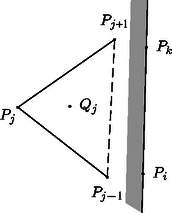
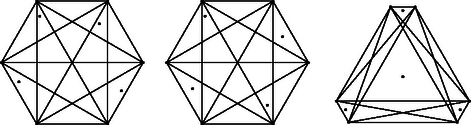
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   1. feladat. Megmutatjuk, hogy létezik a feladat követelményeinek eleget tevő sorozat. Legyen ugyanis $p_1=2$, $p_2=3$, $p_3$, $\text{...}$ a prímszámok (végtelen) növekvő sorozata, és tekintsük az $a_1=6$, $a_2=10$, $a_n=15\cdot p_{n+1}$ ($n\ge 3$) sorozatot. Ebben a sorozatban $a_n$ páratlan szám, ha $n\ge 3$, így nem osztható sem $a_1$-gyel, sem $a_2$-vel, hiszen azok páros számok. Az is világos, hogy $a_1$ és $a_2$ közül egyik sem osztója a másiknak. Ha pedig $n\ge 3$, akkor $p_{n+1}$ osztója $a_n$-nek, de nem osztója a sorozat egyetlen további tagjainak sem, tehát $a_n$ nem lehet osztója a sorozat egy másik elemének. Az első feltétel tehát teljesül. A sorozatban bármely két számnak van 1-nél nagyobb közös osztója. Valóban: $a_1$ és $a_2$ esetén ez a szám 2; $a_1$ és $a_n$ esetén 3, ha $n\ge 3$, végül ha $n$, $m\ge 2$, akkor $a_n$ és $a_m$ is osztható 5-tel. Tehát a második feltétel is teljesül. Végezetül, ha egy pozitív egész osztója a sorozat minden elemének, akkor osztója $a_1$-nek és $a_2$-nak is, és így csak 1 vagy 2 lehet. A második lehetőség azonban könnyen kizárható, hiszen $a_3$ páratlan szám. Ezzel igazoltuk, hogy a sorozat a harmadik feltételt is kielégíti.   Megjegyzések. 1. A fenti sorozatban a második tagtól kezdve minden elem osztható 5-tel. Olyan sorozat is megadható, amelyben a sorozat elemeinek semelyik tagtól kezdve nem létezik 1-nél nagyobb közös osztója. Ilyen sorozat például az $a_{3n+1}=6p_{n+4}$, $a_{3n+2}=10p_{n+4}$, $a_{3n+3}=15p_{n+4}$ ($n\ge 0$) összefüggésekkel definiálható. Az is világos azonban, hogy bármely, a feladat feltételeinek eleget tevő sorozatban lesz végtelen sok elem, amelynek van 1-nél nagyobb közös osztója. (Miért?) 2. A sorozat konstrukciójánál mindenképpen szükség van végtelen sok különböző prímszám segítségére. Nem lehet ugyanis megadni véges sok prímszámot úgy, hogy legyen olyan pozitív egészekből álló végtelen sorozat, amelyben egyik szám sem osztója egyetlen másiknak sem, és amelyben minden szám összes prímosztója az adott prímszámok közül való. Feladat. Bizonyítsuk be a fenti állítást.   2. feladat. Először olyan $p$ polinomot mutatunk, amely az egymástól különböző $a_1$, $a_2$, $\text{...}$, $a_n$ helyeken rendre az egymástól nem feltétlenül különböző $b_1$, $b_2$, $\text{...}$, $b_n$ értékeket veszi fel. Ehhez tekintsük $i=1$, 2, $\text{...}$, $n$ esetén a következő $p_i$ polinomot: $\begin{array}{c}{\displaystyle p_i\left(x\right)=\prod _{\begin{array}{c}\hfill j\ne i\hfill \\ \hfill 1\le j\le n\hfill \end{array}}^{}\frac{x-a_j}{a_i-a_j}\mathrm{.}}\end{array}$ Világos, hogy $p_i\left(a_i\right)=1$ és $p_i\left(a_j\right)=0$, ha $j\ne i$. Ezért a $p\left(x\right)=b_1\cdot p_1\left(x\right)+\text{...}+b_n\cdot p_n\left(x\right)$ összefüggéssel definiált polinom, az ún. Lagrange-féle interpolációs polinom, megfelelő lesz. Könnyen látható, hogy ezen $p$ polinom fokszáma legfeljebb $n-1$. Azonban $p$ még akkor sem lesz mindig egész együtthatós, ha $a_1$, $\text{...}$, $a_n$ és $b_1$, $\text{...}$, $b_n$ egész számok. Legyen most $a_1=1$, $a_2=2$, $\text{...}$, $a_n=n$. Milyen $b_1$, $\text{...}$, $b_n$ egész értékek mellett tudunk egyszerűen következtetni arra, hogy a $p$ polinom együtthatói egész számok? A $p$ polinom minden együtthatója olyan racionális szám, amelynek a nevezője valamilyen $1\le i\le n$ indexre $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle \prod _{\begin{array}{c}\hfill j\ne i\hfill \\ \hfill 1\le j\le n\hfill \end{array}}^{}\left(a_i-a_j\right)}& {\displaystyle =\left(i-1\right)\left(i-2\right)\text{...}\left(i-\left(i-1\right)\right)\left(i-\left(i+1\right)\right)\text{...}\left(i-n\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle ={\left(-1\right)}^{n-i}\left(i-1\right)!\left(n-i\right)!}\hfill \end{array}}}\end{array}$ alakú, számlálója pedig ugyanekkor $b_i$-vel osztható egész szám. Könnyen látható, hogy az így adódó nevezők mindegyike osztója az $N={\left[\left(n-1\right)!\right]}^2$ számnak. Ha tehát a $b_i$ értékek mindegyike osztható $N$-nel, akkor a fenti konstrukcióval létrehozott $p$ polinom egész együtthatós lesz. Az általunk keresett polinomnak azonban az előírt helyeken 2-hatvány értékeket kell felvennie, azok pedig nem oszthatók $N$-nel, ha $n\ge 4$. Hogyan lehet ezen segíteni? Válasszunk ki $n$ darab különböző 2-hatványt, ami ugyanannyi ‐ mondjuk $m$ ‐ maradékot ad $N$-nel osztva. Ezt megtehetjük, hiszen végtelen sok különböző 2-hatvány van. Legyenek ezek $c_1$, $c_2$, $\text{...}$, $c_n$, és tekintsük a $b_i=c_i-m$ ($1\le i\le n$) számokat. Ezekre igaz, hogy $b_i$ osztható $N$-nel, létezik tehát olyan egész együtthatós polinom, amelyre $p\left(i\right)=b_i$ minden 1 és $n$ közé eső $i$ egész számra. Ennek a $p$ polinomnak konstans tagját $m$-mel megnövelve olyan, továbbra is egész együtthatós $p^{*}$ polinomhoz jutunk, amelyre $p^{*}\left(i\right)=c_i$. Ezzel a feladat állítását igazoltuk.   Megjegyzések. 1. A megoldásból kitűnik, hogy különböző 2-hatványok helyett különböző 3-hatványokat vagy éppen különböző prímszámokat is előírhattunk volna a keresett polinom 1, 2, $\text{...}$, $n$ helyen felvett értékeiként. Sőt, még ennél is tovább mehetünk. Mivel $\begin{array}{c}{\displaystyle \left(\genfrac{}{}{0ex}{}{n-1}{i-1}\right)=\frac{\left(n-1\right)!}{\left(i-1\right)!\left(n-i\right)!}}\end{array}$ egész szám, az $a_1=1$, $a_2=2$, $\text{...}$, $a_n=n$ alappontokra épített Lagrange-féle interpolációs polinom együtthatói már akkor is egész számok, ha minden $b_i$ osztható $\left(n-1\right)!$-sal. A skatulya-elv szerint $\left(n-1\right)\left(n-1\right)!+1$ szám között mindig található $n$ olyan, amelyik $\left(n-1\right)!$-sal osztva ugyanolyan maradékot ad. Megfogalmazhatjuk tehát a következő, a feladatban szereplőnél erősebb állítást. Legyen $H$ egy legalább $\left(n-1\right)\left(n-1\right)!+1$ elemű egész számokból álló halmaz. Ekkor létezik olyan, legfeljebb $\left(n-1\right)$-ed fokú egész együtthatós polinom, amelynek az 1, 2, $\text{...}$, $n$ helyeken felvett értékei a $H$ különböző elemei.   3. feladat. Tekintsünk egy $N$ elemű $H$ ponthalmazt, amely megfelel a feladatban szereplő feltételeknek. Tegyük fel, hogy $H$ konvex burkának $n$ csúcsa van. Ezt a konvex $n$-szöget egy csúcsából kiinduló átlói segítségével $n-2$ háromszögre bonthatjuk, amelyek mindegyikében $H$-nak pontosan egy pontja helyezkedik el, a második feltétel értelmében. Egy ilyen háromszög határára ‐ az első feltétel miatt ‐ $H$-nak nem eshet más pontja, mint a szóban forgó háromszög 3 csúcsa. A $H$ halmaz tehát pontosan a konvex burkának a csúcspontjaiból és az előbb említett $n-2$ pontból áll. Ennek következtében $N=2n-2=2\left(n-1\right)$, azaz páros szám. A következőkben megmutatjuk, hogy minden 3-nál nagyobb $N$ páros szám esetén megadható a síkon $N$ pont a követelményeknek megfelelően. Legyen $n=\frac{N+2}{2}$, ekkor $n\ge 3$. Tekintsünk egy tetszőleges $P_0{P}_1\text{...}{P}_{n-1}$ konvex $n$-szöget. Ennek a belsejében vegyünk fel $n-2$ további pontot a következőképpen. Minden $1\le i\le n-2$ esetén legyen $Q_i$ a $P_0{P}_i{P}_{n-1}$ és $P_{i-1}{P}_i{P}_{i+1}$ háromszögek közös részének tetszőleges belső pontja. Azt állítjuk, hogy a $H=\left\{P_0\mathrm{,}{P}_1\mathrm{,}\text{...}\mathrm{,}{P}_{n-1}\mathrm{,}{Q}_1\mathrm{,}\text{...}\mathrm{,}{Q}_{n-1}\right\}$ ponthalmaz megfelel a feltételeknek. Legyen $0\le i<j<k\le n-1$. Azt állítjuk, hogy a $P_i{P}_j{P}_k$ háromszög belseje $H$ pontjai közül egyedül a $Q_j$ pontot tartalmazza. Először azt mutatjuk meg, hogy $Q_j$ valóban a $P_i{P}_j{P}_k$ háromszög belső pontja. A $P_i{P}_j{P}_k$ szögtartomány tartalmazza a $P_0$, $P_j$, $P_{n-1}$ pontokat, és így a $P_0{P}_j{P}_{n-1}$ háromszög minden pontját is. Minthogy $Q_j$ ennek a háromszögnek belső pontja, $Q_j$ a $P_i{P}_j{P}_k$ szögtartomány belsejében van (1. ábra). Hasonlóképpen látható, hogy $Q_j$ a $P_i{P}_k$ egyenesre támaszkodó, $P_j$-t tartalmazó félsík belsejében található, hiszen ez a félsík tartalmazza a $P_{j-1}$, $P_j$, $P_{j+1}$ pontokat, és $Q_j$ a $P_{j-1}{P}_j{P}_{j+1}$ háromszög belső pontja (2. ábra). A $Q_j$ pont tehát az 1. ábrán látható nyílt szögtartomány és a 2. ábrán látható nyílt félsík közös részében van, ez pedig éppen a $P_i{P}_j{P}_k$ háromszög belső pontjainak halmaza. Most megmutatjuk, hogy ez a halmaz $H$ pontjai közül a $Q_j$-n kívül egyetlen pontot sem tartalmaz. A $P_0{P}_1\text{...}{P}_{n-1}$ sokszög konvex, ezért egyik csúcsa sem eshet a $P_i{P}_j{P}_k$ háromszög belsejébe. Tekintsük most valamelyik $Q_l$ pontot, ahol $l\ne j$. Ez a pont a $P_{l-1}{P}_l{P}_{l+1}$ háromszög belsejében helyezkedik el. Ha $l<i$, akkor a $P_0{P}_i$ egyenes elválasztja ezt a háromszöget a $P_i{P}_j{P}_k$ háromszögtől, tehát $Q_l$ valóban nem eshet az utóbbi háromszög belsejébe. Az $i<l<j$, $j<l<k$, illetve $k<l$ esetekben a megfelelő elválasztó egyenesek rendre a $P_i{P}_j$, $P_j{P}_k$ és $P_k{P}_{n-1}$ egyenesek. A 3. ábra az $l=j-1$ esetet szemlélteti. Ezzel állításunkat bizonyítottuk. Hátravan még annak igazolása, hogy $H$ pontjai közül semelyik három nem esik egy egyenesre. A konstrukcióból azonnal következik, hogy semelyik $P_i{P}_j$ egyenes nem illeszkedhet $H$-nak egyetlen további pontjára sem. Ha tehát egy egyenes $H$ pontjai közül hármat is tartalmazna, akkor tartalmaznia kellene legalább két $Q$ típusú pontot. Legyenek ezek $Q_s$ és $Q_t$. A $Q_s{Q}_t$ egyenes a $P_0{P}_1\text{...}{P}_{n-1}$ sokszög kerületét két pontban metszi, jelöljük ezeket $U$-val és $V$-vel. Ha ezek közül az egyik, mondjuk $U$ a sokszög $P_i$ csúcsa volna, akkor $V$ szükségképpen a sokszög valamely $P_j{P}_k$ oldalának belső pontja lenne. Ekkor a $P_i{P}_j{P}_k$ háromszög a $Q_s$ és a $Q_t$ pontokat is tartalmazná, fenti állításunkkal ellentétben. Ha pedig $U$ és $V$ rendre a sokszög $P_i{P}_j$ és $P_k{P}_l$ oldalainak lenne belső pontja (feltehető, hogy $P_i$, $P_j$, $P_k$ és $P_l$ ilyen sorrendben, egy konvex négyszög csúcsai), akkor $H$-nak összes pontja, amely a $Q_s{Q}_t$ egyenesre illeszkedik, a $P_i{P}_j{P}_k{P}_l$ négyszög belsejébe esne. Ez azonban lehetetlen, hiszen a fenti állításból könnyen levezethető, hogy ez a négyszög $H$-nak pontosan két pontját tartalmazza. Ezzel a feladat megoldását befejeztük.   Megjegyzések. 1. Páros $N$ esetén a keresett ponthalmaz létezésére indukciós bizonyítás is adható, amelyet csak vázolunk. Tegyük fel, hogy a $P_0{P}_1\text{...}{P}_{n-1}$ konvex sokszöget, és annak $Q_1$, $\text{...}$, $Q_{n-2}$ belső pontjait már meghatároztuk úgy, hogy semelyik 3 pont nem esik egy egyenesre, és minden $P_i{P}_j{P}_k$ háromszög belsejébe pontosan egy $Q$ pont esik. Vegyük fel a $P_n$ pontot úgy, hogy $P_0{P}_1\text{...}{P}_{n-1}{P}_n$ konvex $\left(n+1\right)$-szög legyen, semelyik $P_n{P}_i{P}_{n+1}$ háromszög ne tartalmazzon egyetlen $Q_j$ pontot sem, továbbá $P_n$ ne legyen rajta egyik olyan egyenesen sem, amely az eddigi pontok közül kettőre már illeszkedik. ,,Látszik'', hogy ezt mindig megtehetjük. A szabatos bizonyítás megfogalmazása azonban egyáltalán nem magától értetődő. Ezek után vegyük fel a $Q_{n-1}$ pontot a $P_{n-1}{P}_i{P}_n$ ($0\le i\le n-1$) háromszögek közös részeinek belsejében, ami éppen a $P_{n-1}{P}_0{P}_n$ és $P_{n-1}{P}_{n-2}{P}_n$ háromszögek közös részének belseje. Eközben vigyázunk arra, hogy $Q_{n-1}$ ne essék egyetlen olyan egyenesre sem, amelyeket az eddigi pontok meghatároznak. A keletkező $\left\{P_0\mathrm{,}{P}_1\mathrm{,}\text{...}\mathrm{,}{P}_n\mathrm{,}{Q}_1\mathrm{,}\text{...}\mathrm{,}{Q}_{n-1}\right\}$ ponthalmaz konvex burka éppen a $P_0{P}_1\text{...}{P}_n$ sokszög, és semelyik 3 pontja nem esik egy egyenesre. Az indukciós feltevésből adódik, hogy a $P_i{P}_j{P}_k$ belsejébe pontosan egy pont esik, ha $n\notin \left\{i\mathrm{,}j\mathrm{,}k\right\}$. A $Q_{n-1}$ pont konstrukciója alapján ugyanez elmondható a $P_{n-1}{P}_n{P}_i$ háromszögekről is. Végül tekintsük bármelyik $P_i{P}_j{P}_k$ háromszöget, ahol $i<j<n-1$. A $P_i{P}_j{P}_{n-1}{P}_n$ négyszögbe, melyet annak $P_j{P}_{n-1}$ átlója a $P_n{P}_{n-1}{P}_j$ és a $P_{n-1}{P}_j{P}_i$ háromszögekre bont, az előzőek alapján pontosan 2 pont esik. Ezek egyike a $Q_{n-1}$ pont, amely a $P_{n-1}{P}_n{P}_i$ háromszög egyetlen belső pontja a tekintett pontok közül. Ezért a másik pont szükségképpen a $P_i{P}_j{P}_{n-1}$ háromszögbe esik, és oda más pont nem is eshet (4. ábra). 2. Ha az $n=3$ esetén felrajzolható, lényegében egyértelmű konstrukcióból kiindulunk, és arra a fenti indukció lépéseit alkalmazzuk, akkor az első megoldásban ismertetett konstrukcióhoz hasonló pontrendszerhez jutunk. Felmerülhet az a gondolat, hogy lehetséges-e ,,geometriailag más szerkezetű'' ponthalmazokat is mutatni, amelyek a feltételeknek szintén megfelelnek. Ilyen ponthalmazokat is képezhetnénk az indukciós eljárás segítségével, ha nem ragaszkodunk ahhoz, hogy a $P_0$, $P_1$, $\text{...}$, $P_n$ csúcspontokkal rendelkező konvex sokszög csúcsai éppen ilyen sorrendben kövessék egymást. Az 5. ábrán három különböző konstrukciót mutatunk $N=10$ ($n=6$) esetén. Károlyi Gyula