Kezdőlap


Cím:	A VII. Horváthországi Országos Matematika Verseny
Szerző(k):	Horváth Bokor Rózsa , Horváth Vilmos
Füzet:	1998/október, 394 - 396. oldal	PDF \| MathML
Témakör(ök):	Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Adriai-tenger partján Kraljevicán május 7. és 10. között rendezték meg Horvátországban a hetedik országos matematika versenyt. A versenyen középiskolások és az általános iskola 7. és 8. osztályos diákjai szerepeltek. Az országos döntőbe meghívásos alapon évfolyamonként 25‐30 legjobb diák vehetett részt. Az iskolai versenyeket általában február végén tartják. A legjobbak indulhatnak a községi versenyen. Ezután következik a megyei erőpróba, ahol évenként kb. 900‐1000 tanuló szerepel.
Az országos döntő egyben jutalomkirándulás is az ott résztvevőknek. Alkalom nyílik a házigazda város és környéke nevezetességeinek megismerésére.
A versenypéldákat a Horvátországi Matematika Társulat bizottsága állítja össze. Évfolyamonként négy-négy feladatot tűznek ki, megoldásukra a versenyzőknek négy óra áll a rendelkezésre. A döntő legjobbjai alkotják Horvátország válogatottját a matematikai
diákolimpián.
Az 1997/98-as év feladatai:

I. évfolyam

1. Melyik tört a nagyobb:

\begin{matrix} A = \frac{2,00 ... .004}{{(1,00 ... .004)}^{2} + 2,00 ... .004} vagy B = \frac{2,00 ... .002}{{(1,00 ... .002)}^{2} + 2,00 ... .002}, \end{matrix}

ha tudjuk, hogy a számlálóban és a nevezőben megadott minden számban 1998 nulla szerepel?

2. Határozzuk meg mindazokat az

m

és

n

természetes számokat, amelyek kielégítik a következő egyenletet:

\begin{matrix} 10 (m + n) = m n . \end{matrix}

3. Iván és Krešo együtt indult el Crkvenicáról Kraljevica felé, míg Márkó velük egyidőben Kraljevicáról Crkvenica felé. A két város közötti távolság 15 km. Hármuknak egy kerékpárja volt. Az úton gyalog 5 km/h, míg kerékpárral 15 km/h sebességgel haladtak. Iván gyalog indult el, míg Krešo a kerékpárt hajtotta, amíg nem találkozott Márkóval. Akkor Krešo odaadta a kerékpárt Márkónak és gyalog folytatta az utat Kraljevica felé, míg Márkó kerékpáron haladt tovább Crkvenica felé. Amikor találkozott Ivánnal odaadta neki a járművet és gyalog érkezett Crkvenicára, míg Iván kerékpáron érkezett Kraljevicára. Melyik fiú mennyi ideig volt úton, mennyi ideig gyalogolt, valamint mennyi ideig kerékpározott?

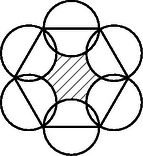
4. Legyen a szabályos hatszög oldalának hossza

a

. Határozzuk meg a besatírozott területet.

II. évfolyam

1.
Oldjuk meg a következő egyenletet

\begin{matrix} 2 z^{3} - (5 + 6 i) z^{2} + 9 i z + 1 - 3 i = 0, \end{matrix}

ha tudjuk, hogy az egyenlet egyik gyöke valós.

2. Bizonyítsuk be, hogy ha

a \geq 0

és

b \geq 0

két tetszőleges valós szám, akkor

\begin{matrix} \frac{a + \sqrt[3]{a^{2} b} + \sqrt[3]{a b^{2}} + b}{4} \leq \frac{a + \sqrt[]{a b} + b}{3} . \end{matrix}

3. Az

A B C D

négyzet

\bar{A B}

és

\bar{B C}

oldalán úgy adott egy-egy pont,

E

és

F

, ebben a sorrendben, hogy teljesül

| B E | = | B F |

. Legyen a

\bar{B N}

B C E

háromszög magassága. Bizonyítsuk be, hogy a

D N F

háromszög derékszögű.

4. Legyen

m

és

n

természetes szám, valamint

a = {(n + 1)}^{m} - n

és

b = {(n + 1)}^{m + 3} - n

*	a)Igazoljuk, hogy ha $m$ nem osztható hárommal, akkor $a$ és $b$ relatív prímek.

*	b)Határozzuk meg mindazokat az $m$ és $n$ számokat, amelyekre az $a$ és $b$ számoknak van közös osztójuk.

III. évfolyam

1. Bizonyítsuk be, hogy bármely háromszögre teljesül a szokásos jelölésekkel:

\begin{matrix} (\frac{b}{c} + \frac{c}{b}) cos α + (\frac{c}{a} + \frac{a}{c}) cos β + (\frac{a}{b} + \frac{b}{a}) cos γ = 3. \end{matrix}

2. Egy kúpba félgömböt írunk úgy, hogy alapköreik egybeessenek. Legyen a kúp felületének (az alappal együtt) és a félgömb felületének (az alaplap nélkül) az aránya

k = \frac{18}{5}

. Határozzuk meg a kúp csúcsánál lévő szög nagyságát.

3. Legyenek az

A B C

háromszög magasságvonalai

\bar{A A_{1}}

\bar{B B_{1}}

\bar{C C_{1}}

és teljesüljön a követlező vektoregyenlet:

\begin{matrix} \vec{A A_{1}} + \vec{B B_{1}} + \vec{C C_{1}} = \vec{0} . \end{matrix}

Bizonyítsuk be, hogy az

A B C

háromszög egyenlő oldalú.

4. Bizonyítsuk be, hogy bármely 79 egymást követő természetes szám között található legalább egy olyan szám, amelyben a számjegyek összege osztható 13-mal.
Találjunk olyan 78 egymást követő természetes számból álló sorozatot, amelynek minden tagjára érvényes, hogy számjegyeik összege nem osztható 13-mal.

IV. évfolyam

1. Bizonyítsuk be, hogy az

y^{2} = 4 a x

parabola minden olyan húrja, amelyik egyben átfogója egy derékszögű háromszögnek, amelynek derékszögű csúcsa egybeesik a koordinátarendszer középpontjával, egy pontban metszi egymást.

2. Legyenek

a

és

m

természetes számok, és

p

olyan páratlan prímszám, amelyre teljesül

p^{m} ∤ a - 1

és

p^{m + 1} ∤ a - 1

. Bizonyítsuk be, hogy ekkor:

*	a) $p^{m + n} ∣ a^{p^{n}} - 1$ minden $n \in N$ esetén,

*	b) $p^{m + n + 1} ∤ a^{p^{n}} - 1$ minden $n \in N$ esetén.

3. Legyen

A = {1

, 2, 3,

...

2 n}

, és definiáljuk a

g : A \to A

függvényt a következőképpen:

g (k) = 2 n - k + 1

. Létezik-e olyan

f : A \to A

függvény, amelyre teljesül, hogy

f (k) \neq g (k)

minden

k \in A

és

f (f (f (k))) = g (k)

minden

k \in A

esetén, ha
a)

n = 999

, b)

n = 1000

4. Elhelyeztünk nyolc villanykörtét egy kör mentén. Bármely égő felkapcsolható vagy lekapcsolható. Egy átállításkor egyszerre változtatjuk meg minden égő állapotát, a következő szabály szerint: az az égő, amelynek egyik szomszédja világít, míg a másik nem, a következő állapotban nem fog világítani, viszont az az égő, amelynek mindkét szomszédja egyszerre világít vagy egyszerre nem világít, az átállítás után világítani fog.
Bizonyítsuk be, hogy legfeljebb négy átállítás után minden égő világítani fog.

Horváth Vilmos
Horváth Bokor Rózsa