Cím: Tudósítás az Izsák Imre Gyula versenyről
Szerző(k):  Kiss Zsolt 
Füzet: 1998/április, 205 - 208. oldal  PDF  |  MathML 
Témakör(ök): Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A zalaegerszegi Zrínyi Miklós Gimnázium 1997-ben hatodik alkalommal hirdette meg az Izsák Imre Gyula komplex természettudományi (meghívásos) versenyt matematika, fizika és számítástechnika tantárgyakból. Az idei versenyt rendhagyó módon csillagászati totó is színesítette.
A verseny rendje: A versenyzők mindhárom tantárgyból kaptak feladatot, amelyek megoldására két-két óra állt rendelkezésükre. Használható segédanyagok: az OKTV-n meghatározottak. A számítástechnika versenyen a tanulók IBM PC gépen dolgozhattak PASCAL vagy BASIC nyelven.
A feladatokat az Eötvös Loránd Tudományegyetem tanárai állították össze, és ők alkották a zsűrit is: matematikából Hortobágyi István, fizikából Bérces György, számítástechnikából Zsakó László.
A versenyen 14 gimnázium két-két tanulója indult. Az összetett versenyben (mindhárom tárgy összesített eredménye alapján):

I. helyezett: Végh László, Debrecen, Fazekas Mihály Gimnázium; 
II. helyezett: Váry Mátyás, Zalaegerszeg, Zrínyi Miklós Gimnázium; 
III. helyezett: Karádi Richárd, Győr, Révai Miklós Gimnázium.
Tantárgyi első helyezettek:

matematika: Horváth Gábor, Debrecen, Fazekas Mihály Gimnázium, 
fizika: Császár Balázs, Szombathely, Premontrei r. Szent Norbert Gimnázium, 
számítástechnika: Várkonyi Dániel, Székesfehérvár, Teleki Blanka Gimnázium.
A nyerteseknek a díjakat a LOGITRON, a STARTUP BT és a PROCOMB Kft ajánlotta fel. A verseny megrendezését támogatták: a Pro Renovanda Cultura Hungariae Alapítvány és a ZALA Megyei Pedagógiai Intézet.
Kiss Zsolt
a verseny szervezője

 
A versenyben kitűzött feladatok

 
 
Matematika
 
 

 
1. Igazoljuk, hogy ha n  1-nél nagyobb természetes szám, akkor
2748<1n+1+1n+2...+12n<1.(10 pont)

 
2. Tekintsük az A1B1C1 és a hozzá hasonló, kétszer akkora oldalakkal rendelkező, ellenkező körüljárású, tetszőleges A2B2C2 háromszöget. Bizonyítsuk be, hogy az A1A2, B1B2, C1C2 szakaszok A1, B1, C1-hez közelebbi harmadolópontjai egy egyenesen helyezkednek el. (12 pont)
 
3. Oldjuk meg a következő egyenletet, ha x és y természetes szám:
1+1x-1996+1y-1996=1995(x-1996)(y-1996)(12 pont)

 
4. Bizonyítsuk be, hogy egy tetszőleges tetraéder felszíne legfeljebb az oldalélei négyzetösszegének 36-szorosával lehet egyenlő. Mikor áll fenn az egyenlőség? (16 pont)
 
 
Fizika
 
 

 
1.
  U=25 V        t(min, sec)      7'12''      14'30''      21'52''      29'14''     V(cm3)      5,0      10,0      15,0      20,0     I(mA)      88,5      89,3      89,7      89,8   
Hoffman-vízbontó készülékben szobahőmérsékleten (t=20∘C) fejlődő hidrogéngáz térfogatának időbeli változását mutatja a mellékelt táblázat. (A kísérletek közben mért áramerősség-értékek kiolvashatók a táblázatból.) Határozzuk meg az elemi töltés nagyságát.
 
2.
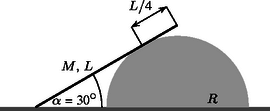
Vízszintes asztalon fekvő R sugarú, rögzített félgömbre egy M tömegű, L hosszúságú rúd támaszkodik. A rúd és a félgömb közötti súrlódás elhanyagolható. Mekkora az asztal és a rúd között fellépő μt tapadási súrlódási együttható értéke, ha a rúd az asztallappal α=30∘-os szöget zár be?
 
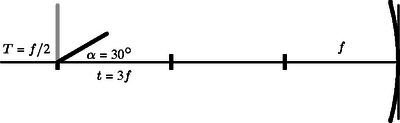
3. f=1 m fókusztávolságú, homorú lencse előtt t=3 m-re egy T=0,5 m magas, világító egyenes fényforrás áll, az optikai tengelyre merőlegesen. A fényforrást megdöntjük úgy, hogy az α=30∘-os szöget zárjon be az optikai tengellyel. Szerkesztéssel és számolással is határozzuk meg a fényforrás képének helyét és nagyságát.
 
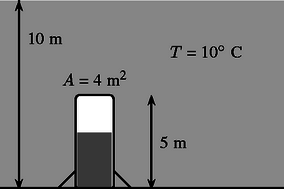
4. Egy L=5 m hosszúságú, A=4m2 keresztmetszetű, felső végén zárt vasbetonhengert 10 m mély tó fenekére eresztettek le (leeresztése során mindvégig függőlegesen tartva). A tó és a levegő hőmérséklete egyaránt 10∘ C.
a) Mekkora a hengerben levő levegőoszlop magassága?
b) Mennyi hőt kellene közölni a henger belsejében levő levegővel, hogy a hengerben csak levegő maradjon?
 
 
1997. Számítástechnika
 
 

 
1. feladat. Galton-deszka szimuláció (100 pont)
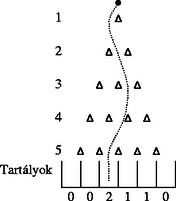
1. ábra (n=5 esetén)
Azt, hogy a binomiális eloszlásnak ,,köze van'' a normális eloszláshoz, a matematikusok sokféle tételben megfogalmazták. Készítsünk a két eloszlás ,,rokonságának'' igazolására kísérleti eszközt a következő elképzelésre építve! Egy deszkában n sorban szabályosan elrendezve ékeket helyezünk el, a k-adik sorban éppen k darabot (1. ábra). Golyókat indítunk útnak legfelül, egymás után, amelyek az ékeken véletlenszerűen eltérülve hullanak lefelé, míg végül a legalul elhelyezett n+1 tartály valamelyikében landolnak. Az ékek 1/2 (P) valószínűséggel térítik el a golyót balra, illetve jobbra. Sok-sok golyóval elvégezve a kísérletet, a normális eloszlás haranggörbéjére emlékeztető alakzat fog kialakulni a lehullott golyók ,,oszlopaiból''.
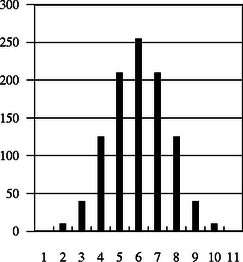
2. ábra (n=10 esetén)
Ezt az ún. Galton-deszka kísérletet kell számítógéppel imitálnod. A program paraméterként kérje be a sorok számát (n), valamint az egyes ékekről való balra eltérülés valószínűségét (P). Rajzold ki a Galton-deszkát a képernyőre, majd billentyűvel vezérelhető sebességgel ,,kövesd'' útjukon a golyókat. Az egyes tartályokba leérkező golyók száma jelenjen meg a tartályoknál, a relatív gyakorisága pedig egy hisztogramon (2. ábra), a felhasználó által kívánt golyószámonként kirajzolva. Ha nagyon gyors mozgást kíván, akkor elegendő minden ‐ mondjuk ‐ 100-adik időegységben újrarajzolni a hisztogramot, ha pedig nagyon lassan, akkor minden egyes golyó után. Mindez addig tartson, amíg a felhasználó meg nem unja.