Kezdőlap


Cím:	Egy hagyományos amerikai matematikaverseny (PUTNAM)
Füzet:	1998/április, 203 - 205. oldal	PDF \| MathML
Témakör(ök):	Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A William Lowell Putnam nevét viselő matematikaverseny 1938-ban indult. Az Egyesült Államok és Kanada főiskoláin és egyetemein minden évben megrendezik. A névadó az egykori harvardi diák 1921-ben cikket írt az iskola folyóiratába, amelyben egy főiskolák közötti szellemi vetélkedés előnyeire hívta fel a figyelmet. Halála után özvegye hozta létre a William Lowell Putnam főiskolák közötti emlékalapítványt. Az első versenyt angol nyelvből rendezték, és csak pár évvel később indult matematikából. Az özvegy 1935-ben bekövetkezett halála óta az Amerikai Matematikai Társulat szervezi a vetélkedőt.
Résztvevő lehet minden Egyesült Államokbeli és kanadai egyetemi és főiskolai hallgató, aki még nem szerezte meg a diplomáját, de minden diák összesen csak négy alkalommal vehet részt ezen a versenyen.
Érdekes a verseny lebonyolításának rendje: Három fős csapatok indulnak, de minden versenyző egyénileg írja a dolgozatát. Két részből áll a verseny, mindkettő három órás, közötte két óra szünettel. Minden városban egyszerre kell megírni, ezért a kontinens időeltolódásait is figyelembe vevő általános időbeosztást készítettek. A tavaly december 6-án megrendezett Putnam versenyen Magyarországon tanuló amerikai diákok is résztvettek a szigorú szabályoknak megfelelően.
A legutóbbi tíz évben a Harvard és a Duke Egyetem csapatai felváltva nyertek. A tavalyi versenyen az első öt helyzett a Harvard, a Duke, a Princeton, a Massachusetts és a Washington egyetem volt. Az első helyezett csapat díja 25 000 dollár és minden csapattag külön 1000 dollárt kap.
A múlt évi versenyen egy Amerikában tanuló magyar diák, a KöMaL matematika és fizika pontversenyeiből már jól ismert Katz Sándor dicséretben részesült.

Az 58. William Lowell Putnam matematikaverseny feladatai, 1997. december 6.

A1. A

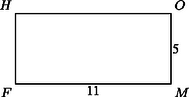
H O M F

téglalapban

H O = 11

egység,

O M = 5

egység. Egy

A B C

háromszögben a magasságvonalak metszéspontja a

H

, a körülírt körének középpontja az

O

, a

B C

szakasz felezőpontja az

M

, az

A

-ból húzott magasság talppontja az

F

. Milyen hosszú a

B C

szakasz?

A2. Egy kerek asztal körül

n

játékos ül, mindegyiknek van 1 pénzérméje. Az első játékos átad 1 pénzérmét a második játékosnak, aki ezután átad 2 érmét a harmadiknak. A harmadik játékos ismét 1 érmét ad a negyediknek, aki megint 2-t ad az ötödiknek. És így tovább, a játékosok felváltva 1 vagy 2 érmét adnak át a következő olyan játékosnak, akinek még van pénze. Akinek elfogy a pénze, az kiesik a játékból. Keressünk végtelen sok olyan

n

számot, amelyre valamelyik játékos birtokába kerül mind az

n

pénzdarab.

A3. Számítsuk ki az integrál értékét:

\begin{matrix} \int_{0}^{\infty} (x - \frac{x^{3}}{2} + \frac{x^{5}}{2 \cdot 4} - \frac{x^{7}}{2 \cdot 4 \cdot 6} + ...) \cdot (1 + \frac{x^{2}}{2} + \frac{x^{4}}{2^{2} \cdot 4^{2}} + \frac{x^{6}}{2^{2} \cdot 4^{2} \cdot 6^{2}} + ...) d x . \end{matrix}

A4. Legyen

G

egy csoport,

e

az egységeleme, és

φ : G \to G

olyan függvény, amelyre

\begin{matrix} φ (g_{1}) φ (g_{2}) φ (g_{3}) = φ (h_{1}) φ (h_{2}) φ (h_{3}) \end{matrix}

teljesül, valahányszor

g_{1} g_{2} g_{3} = e = h_{1} h_{2} h_{3}

. Bizonyítsuk be, hogy létezik

G

-nek egy olyan

a

eleme, amelyre a

ψ (x) = a φ (x)

leképezés homomorfizmus. (Azaz

ψ (x y) = ψ (x) ψ (y)

minden

x

y \in G

-re.)

A5. Jelölje

N_{n}

az olyan

(a_{1}, a_{2}, ..., a_{n})

pozitív egész rendezett

n

-esek számát, amelyekre

\frac{1}{a_{1}} + \frac{1}{a_{2}} + ... + \frac{1}{a_{n}} = 1

. Határozzuk meg, hogy

N_{10}

páros-e vagy páratlan.

A6. A pozitív egész

n

és tetszőleges

c

valós számra definiáljuk

x_{k}

-t a következő rekurzióval:

x_{0} = 0

x_{1} = 1

, és minden

k \geq 0

-ra

\begin{matrix} x_{k + 2} = \frac{c x_{k + 1} - (n - k) x_{k}}{k + 1} . \end{matrix}

Rögzítsük az

n

-et, és tekintsük azt a legnagyobb

c

értéket, amelyre

x_{n + 1} = 0

. Adjuk meg

x_{k}

-t

n

és

k

függvényében (

1 \leq k \leq n

B1. Jelölje

{x}

x

valós számnak a legközelebbi egész számtól való távolságát. Tetszőleges pozitív egész

n

-re határozzuk meg az

\begin{matrix} S_{n} = \sum_{m = 1}^{6 n - 1} {min}_{}^{} ({\frac{m}{6 n}}, {\frac{m}{3 n}}) \end{matrix}

értéket. (

{min}_{}^{} (a, b)

jelöli az

a

és

b

minimumát.)

B2. Legyen

f

egy kétszer differenciálható valós értékű függvény, amelyre teljesül az

\begin{matrix} f (x) + f'' (x) = - x g (x) f' (x) \end{matrix}

egyenlőség, ahol

g (x) \geq 0

minden valós

x

-re. Bizonyítsuk be, hogy

| f (x) |

korlátos.

B3. Tetszőleges pozitív egész

n

-re írjuk fel a

\sum_{m = 1}^{n} \frac{1}{m}

összeget

\frac{p_{n}}{q_{n}}

alakban, ahol

p_{n}

és

q_{n}

relatív prím pozitív egészek. Határozzuk meg az összes olyan

n

-et, amelyre a

q_{n}

nem osztható 5-tel.

B4. Jelölje az

{(1 + x + x^{2})}^{m}

hatványban az

x^{n}

együtthatóit

a_{m, n}

. Bizonyítsuk be, hogy minden

k \geq 0

esetén

\begin{matrix} 0 \leq \sum_{i = 0}^{⌊ 2 k / 3 ⌋} {(- 1)}^{i} a_{k - i, i} \leq 1. \end{matrix}

B5. Bizonyítsuk be, hogy minden

n \geq 2

-re

\begin{matrix} 2^{2^{.^{.^{.^{2}}}}}}^{n} \equiv 2^{2^{.^{.^{.^{2}}}}}}^{n - 1} (mod n) . \end{matrix}

B6.
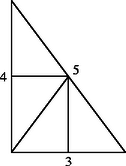
Egy háromszög feldarabolásakor képezzük az összes olyan pontpár távolságát, amelyek ugyanazon részbe esnek. A kapott távolságok halmazának legkisebb felső korlátját nevezzük a feldarabolás átmérőjének.
A 3, 4, 5 oldalú derékszögű háromszög ábra szerinti feldarabolásában például az ,,átmérő''

5 / 2

.
Mennyi a lehető legkisebb ,,átmérő'', amelyet e háromszög 4 részre darabolásával kaphatunk?