|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Simonyi Károly: A fizika kultúrtörténete és Sain Márton Nincsen királyi út című könyvében is megtalálható Arkhimédész gyönyörű gondolatmenete a parabolaszelet területének meghatározásáról: Arkhimédész be akarta bizonyítani, hogy egy ,,parabola szegment'' területe egyenlő a beírt háromszög területének 4/3-adszorosával. Ehhez a parabola néhány tulajdonságának ismeretére volt szüksége. A fenti művekben néhány tétel igazolásánál koordináta-geometriai levezetések szerepelnek. Ebben a cikkben a párhuzamos szelők tételének és háromszögek hasonlóságának segítségével fogjuk az egyik tételt belátni. Közben a parabola (és a többi másodrendű görbe) elemi tulajdonságainak bizonyításához alkalmas módszert is láthatunk.
Tudjuk, hogy a parabola a sík azon pontjainak halmaza, amelyek a sík egy egyenesétől, a vezéregyenestől () és egy ‐ nem az egyenesen lévő ‐ pontjától, a fókusztól () egyenlő távolságra vannak.
Fogalmazzuk át a fenti definíciót: Parabola azon körök középpontjainak halmaza, amely körök átmennek a fókuszon és érintik a vezéregyenest.
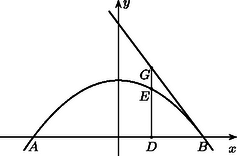
Az 1. ábrán az és a az fókuszú, vezéregyenesű parabola pontjai. A definícióból rögtön kitűnik, hogy a parabola szimmetrikus az -en átmenő, a -re merőleges egyenesre (tengely).
Ennek ismeretében tudunk parabolapontot szerkeszteni: Felveszünk a vezéregyenesen egy pontot, ezen át párhuzamost húzunk -vel, majd ezt az felezőmerőlegesével () messük el, az így kapott pont pontja a parabolának.
Lássuk be, hogy -nak csak egy közös pontja van a parabolával.
Legyen , . Ekkor , és ez nagyobb, mint -nek a -től való távolsága. Azt is beláttuk itt, hogy az összes pontja, -t kivéve, távolabb van -től, mint -től, azaz külső pont (1. ábra).
Azt sem nehéz megmutatni, hogy az -n átmenő összes egyenes közül egyedül az -nak van meg a fenti tulajdonsága. Joggal nevezzük -t a parabola -beli érintőjének. (Vegyünk egy, az -n átmenő, -tól különböző, -re nem merőleges egyenest, tükrözzük erre -et: képe , majd az -n átmenő, -vel párhuzamos egyenesnek és -nek a metszéspontjáról lássuk be, hogy közelebb van -hez, mint -hez, azaz belső pont. Ha viszont merőleges -re, akkor az ,,fölötti'' pontok lesznek a parabola belső pontjai.)
Igaz tehát a következő 1. állítás: A vezéregyenes bármely pontját a fókusszal összekötő szakasz felező merőlegese a parabola érintője annak a pont ,,fölötti'' pontjában.
Két érintő metszéspontja (az 1. ábrán ) viszont éppen felező merőlegesén van rajta, hiszen az háromszögben két oldal felező merőlegesének metszéspontja. Ezért igaz az alábbi:
2. állítás. A parabola két pontját (-t és -t) összekötő szakasz felezőpontja és a pontokban húzott érintők metszéspontja egy, a -vel párhuzamos egyenest határoz meg.
Az Arkimédész által kimondott tétel (ld. Simonyi Károly: A fizika kultúrtörténete c. könyv 75‐78. oldalán) a következő:
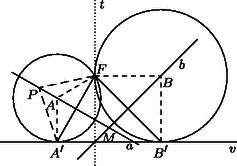
Tétel. ,,Húzzuk meg a parabola egy tetszés szerinti abszcisszájához tartozó ordinátát'' (2. ábra: most a parabola tengelye az tengely). Ennek talppontja , metszéspontja a parabolával . a ponthoz tartozó érintőval . Bárhol is vettük fel a pontot, érvényes a következő:
Ezt fogjuk bizonyítani a parabola tetszőleges húrján levő pontra.
Bizonyítás.
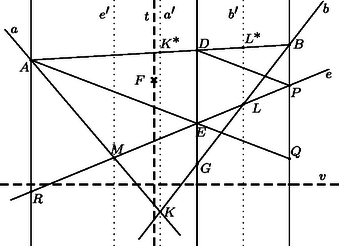
A 3. ábrán a parabola húrja, ezen van a pont. Az , , parabolapontokhoz húzott érintők , és . A 2. állítás szerint az -ban és -ben húzott érintők metszéspotja és az szakasz felezőpontja egy, a tengellyel párhuzamos egyenest határoz meg. Hasonlóan az szakasz felezőpontja és az és érintők metszéspontja, a tengellyel párhuzamos egyenest határozza meg. A szakasz felezőpontja és a és érintők metszéspontja a tengellyel párhuzamos egyenest határozza meg, ennek -vel való metszéspontja .
Előbb belátjuk, hogy párhuzamos -vel, ahol a -n átmenő, tengellyel párhuzamos egyenesnek az érintővel való metszéspontja. | |
(a párhuzamos szelők tétele szerint), amiért .
Így az és párhuzamos állású háromszögek, ahol az érintő és az -n keresztül a tengellyel párhuzamosan húzott egyenes metszéspontja. Mivel az szakasz felezőpontja , az felezőpontja az , így az és háromszögek is hasonlók. Tehát valóban .
Használjuk ki, hogy , ahol az és egyenesek metszéspontja, és miatt .
A párhuzamos szelők tételéből következik, hogy és a fenti egyenlőségek miatt ez utóbbi egyenlő -vel, tehát , és ezt akartuk bizonyítani.
Megjegyzés. Láthatunk most egy olyan feladatot, amely igen egyszerű, és látszólag semmi köze a fentiekhez:
Az középpontú arányú, =val jelölt középpontos hasonlóságnál az paralelogramma képe az . A paralelorgamma átlinak metszéspontja , a képe a , azaz . Legyen az tükörképe a -ra a és a -re a . Ekkor igaz, hogy , és például , illetve , valamint átmegy -n, -n és -n.
Mi köze ennek a fenti parabolás feladathoz?
Bohner Géza, tanár
Kossuth L. Gimn., Cegléd
|
 PDF | MathML
PDF | MathML