A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Egy geometriai feladatpár
Legyen adva az síkon három pont, , és , melyek egy hegyesszögű háromszöget alkotnak. A pontokkal kapcsolatban két feladatot fogalmazunk meg, és célunk a két feladat kapcsolatának vizsgálata.
1. feladat: Keresendő az a pont, amelynek össztávolsága az adott pontoktól, azaz az összeg, minimális. A feladat formálisan az alábbi módon írható le:
2. feladat: Fektessünk át az , , pontokon egy-egy egyenest úgy, hogy a keletkező háromszög szabályos legyen. Keresendő az összes ilyen háromszög közül az, amelyiknek legnagyobb a magassága. Jelölje a háromszög magasságát. Ekkor a feladat formálisan felírva a következő: | | (2) |
Megjegyezzük, hogy nem teljesen nyilvánvaló, hogy a feladatoknak van optimális megoldása, azaz van olyan pont, illetve háromszög, amelyre a keresett magasság maximális, illetve minimális, de az optimális megoldások létezését be fogjuk bizonyítani.
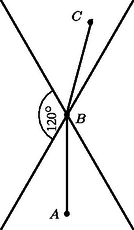
Tegyük fel, hogy az legkisebb szöge, ha több ilyen is van, akkor az egyik ilyen, a csúcsnál van. Vegyünk fel az ponton keresztül egy olyan egyenest, amelynek és ugyanazon az oldalán fekszik. Ez lesz az első oldalegyenese. Ekkor egyértelműen meghatározott az a két, és egyenes, amely keresztül megy a ponton, és az egyenessel 60 fokos szöget zár be. Azt állítjuk, hogy az és pont a két egyenes közül legalább az egyik esetében az egyenes ugyanazon oldalán fekszik, megengedve azt is, hogy és rajta legyen az egyenesen. Ha ugyanis nem így volna, akkor és az és által alkotott két csúcsszögpár egyikének két különböző szögtartományának belsejében volna, ami azt jelenti, hogy az szög nagyobb 60 foknál, ami lehetetlen, hiszen így az szögeinek összege nagyobb volna 180 foknál (1. ábra). A keresett második oldalegyenesének és közül azt választjuk tehát, amelynek ugyanazon oldalán fekszik és . Ekkor a háromszög harmadik, -n keresztül menő egyenese egyértelműen meghatározott. Mivel a kiindulásul szolgáló egyenest végtelen sokféleképpen lehet felvenni, ezért a (2) feladatban a maximumot egy végtelen halmazon keressük.
Az oldalegyenesei hét részre osztják fel az síkot. A háromszög maga egy ezek közül, három egy-egy szöge csúcsszögének szögtartománya, míg további három szögeinek szögtartományából az a rész, amely a háromszögön kívül fekszik. Tegyük fel, hogy a pont az csúcsnál fekvő szög csúcsszögének tartományában van (2. ábra). Ekkor a szög legalább akkora, mint a szög kiegészítő szöge, tehát a szög tompa szög. Innen az adódik, hogy a oldala nagyobb, mint a oldal. Hasonlóképp a háromszögben rövidebb, mint . Tehát a pont helyett előnyösebb az pontot választani, hiszen = . Tegyük most fel, hogy a pont az csúcsnál fekvő szög szögtartományának a háromszögön kívül eső részében van. Legyen az szakasz metszéspontja a oldallal. Az és szögek közül az egyik legalább derékszög. Az általánosság megszorítása nélkül feltehetjük, hogy ez az szög. Tehát a szög is legalább derékszög, így a leghosszabb oldala . Innen már megmutatható, hogy az pont jobb választás, mint . Ugyanis . Az utolsó lépésben az -re vonatkozó -egyenlőtlenséget használtuk fel. Tehát az 1. feladathoz tartozó optimális pontot az -ben kell keresni.
Az alábbiakban bebizonyítunk két tételt a feladatpárra vonatkozóan. A tételek tipikusak abban az értelemben, hogy valahányszor dualitásról beszélünk valamely feladatpár esetén, akkor ugyanilyen szerkezetű tételeket igyekszünk bizonyítani.
1. tétel: Legyen az hegyesszögű, és ennek egy tetszőleges pontja . Legyen egy tetszőleges olyan szabályos háromszög, amelynek oldalegyenesei átmennek az , és pontokon. Jelölje a háromszög magasságát. Ekkor | | (3) |
Bizonyítás: Tegyük fel, hogy az , , pontok rendre a , és oldalakon vannak.
A szabályos háromszög területét egyértelműen meghatározza a magassága, minél nagyobb a magasság, annál nagyobb a terület. Az -et a pont az , és háromszögekre bontja, tehát az előbbi területe az utóbbiak területeinek összege. A , és szakaszok legalább akkorák, mint az utóbbi háromszögek magasságai. Felhasználva, hogy az szabályos, területére a következő becslést kapjuk. | |
Innen -vel való osztás útján adódik az állítás.
2. tétel: Legyen az hegyesszögű az síkon. Legyen egy tetszőleges olyan szabályos háromszög, amelynek oldalegyenesei átmennek az , és pontokon. Jelölje a háromszög magasságát. Ekkor | | (4) |
Bizonyítás: A fentiek szerint elegendő csak a háromszögbe eső pontokat vizsgálni. Az előző tételből következik, hogy ha találunk egy pontból és egy -ből álló párt, amelyre teljesül, akkor a pont az 1. feladatnak, az háromszög a 2. feladatnak optimális megoldása. Ugyanis a (3) egyenlőtlenséget alkalmazva az adott esetre azt kapjuk, hogy bárhogy is válasszuk meg a pontot és az háromszöget, a háromszög magassága nem lehet nagyobb, mint . Tehát ha egyenlő vele, akkor a lehető legnagyobb, azaz maximális. Hasonlóan okoskodva az összeg esetében azt kapjuk, hogy ha az egyenlőség teljesül, akkor az összeg értéke a lehető legkisebb, azaz minimális. Ilyen pár pedig létezik, válasszuk ugyanis a pontnak azt, ahonnan az mindhárom oldala 120 fok alatt látszik. (Ez a pont megkapható, mint az és oldalak fölé írt megfelelő látókörök metszéspontja.) Az -et pedig azok az egyenesek alkotják, amelyek az , , szakaszokra rendre az , , pontokban merőlegesek. Ezért felhasználva a háromszög szabályos voltát nyerjük, hogy | |
Másfelől tudjuk, hogy | |
A két egyenlőtlenséget egybevetve azonnal adódik a kivánt állítás.
Duális feladatpárok általában
A fentiekben egy minimalizálási és egy maximalizálási feladatból álló párt láttunk. Összefoglaló néven mindkettő optimalizálási feladat. Egy optimalizálási feladat mindig valamilyen matematikai objektumokra vonatkozik. Ezek az 1. feladat esetében pontok, a 2. feladatnál háromszögek voltak. Az optimalizálási feladat két részből áll: egyrészt feltételekből, amelyeket a feladatban szereplő objektumoknak ki kell elégíteni, másrészt egy célfüggvényből, amely értékeli az objektumokat. A feladat abban áll, hogy a feltételeket kielégítő objektumok közül a célfüggvény szerinti legjobbat találjuk meg, ha ilyen egyáltalán létezik, és legalább egyet, ha több legjobb is létezik. Az utóbbi esetben természetesen mindegyik legjobbhoz ugyanaz a célfüggvényérték tartozik. A feltételeket kielégítő objektumokat megengedett megoldásoknak, a legjobbakat pedig optimális megoldásoknak nevezzük. Az 1. feladat esetén a megengedett megoldások azok a pontok voltak, amelyek az -gel egy síkban fekszenek, a 2. feladatban pedig azok a háromszögek, amelyek szabályosak, és oldalegyeneseik átmennek az , , pontokon. Az optimális megoldás az 1. feladat esetén az a pont, amelynek az össztávolsága az , , pontoktól a legkisebb, a 2. feladatban pedig az a háromszög, amelynek magassága a legnagyobb.
Első tételünk azt mondta ki, hogy a minimalizálási feladat bármely megengedett megoldásához tartozó ezen feladatbeli célfüggvényérték legalább akkora, mint a maximalizálási feladat bármely megengedett megoldásához tartozó célfüggvényérték az utóbbi feladatban. Ha egy maximalizálási-minimalizálási feladatpárra egy ilyen állítás teljesül, akkor a maximalizálási feladatot primál, feladatnak, a minimalizálásit pedig a duálisának mondjuk, a tételt pedig gyenge dualitási tételnek nevezzük. Innen természetesen azonnal következik, hogy a minimalizálási feladat célfüggvénye legalább akkora, mint a maximalizálási feladaté. Erős dualitási tételről akkor beszélünk, ha azt is sikerül bebizonyítani, hogy az optimális célfüggvényértékek egyenlők. Esetünkben ez volt a 2. tétel. Ha egy feladatpárra csak a gyenge dualitási tétel igaz, de az erős nem, azaz van olyan eset, amikor a minimalizálási feladat célfüggvénye határozottan nagyobb, mint a maximalizálási feladaté, akkor dualitási gyepűről beszélünk. Az alábbiakban mindkettőre látunk példát.
A lineáris programozás esete
Nézzük meg a bérbeadás kérdését most egy bonyolultabb helyzetben. Egy gyár optimális gyártási tervét kell meghatározni egy bizonyos időszakra. Tegyük fel, hogy a gyárban összesen gép van. Ismert a gyár ezen gépeinek kapacitása az adott időszakban, pontosabban szólva az az időtartam, amennyit legfeljebb dolgozhatnak. Ez gépenként különböző lehet, mert egyes gépeket különböző ideig kell karbantartani, hogy a meghibásodást megelőzzék, más gépeknek a személyzete szabadságra megy, stb. Jelölje az 1, 2, , gépek kapacitását , , , . Tegyük fel továbbá, hogy a gyárban terméket állítanak elő. A gépek és a termékek kapcsolatát az fejezi ki, hogy egy termék egy egységének gyártása az egyes gépeken mennyi ideig tart. Az 1, 2, , termékek esetén jelölje , , , azt az időtartamot, amit egységnyi termék gyártása az első gépen igényel. A második gép esetében ugyanezeket a mennyiségeket jelölje , , , , és így tovább, az -edik gép esetén legyenek ezek az időtartamok , , , . Végezetül feltesszük, hogy ismert, hogy az 1, 2, , termékek egy egységén mennyi a haszon, melyet rendre , , , jelöl. Feladatunk meghatározni, hogy mit gyártson az üzem úgy, hogy minden gép el tudja látni a rá váró feladatokat, azaz a legyártandó termékek ne kívánjanak több időt tölteni rajta összesen, mint a kapacitása az adott időszakban, és a vállalat haszna maximális legyen. Az egyes temékekből gyártandó, egyelőre még ismeretlen, mennyiségek legyenek , , , . Ez azt jelenti például, hogy az első termékből legyártandó teljes mennyiség a harmadik gépen időt fog eltölteni. Ha a harmadik gépre az összes ilyen mennyiséget összegezzük, akkor kapjuk meg, hogy a termelési terv szerint a harmadik gépnek mennyit kellene dolgoznia, és ez nem lehet több, mint a gép kapacitása. Természetesen ennek nemcsak a harmadik gépre kell teljesülnie, hanem valamennyi gépre. Így a következő feltételekhez jutunk: | | (5) |
A változók értéke negatív nem lehet, mert ez azt jelentené, hogy valamelyik terméket nem gyártjuk, hanem vásároljuk. Ezt formálisan kifejezve kapjuk, hogy Mivel a második termék egy egységén a nyereségünk, ezért, ha a gyártott mennyiség , akkor ezen a terméken a nyereség lesz, a teljes nyereség pedig az ilyen tagok összege. Tehát a célfüggvényünk | | (7) |
lesz.
Az a feladat, amely az (5) és (6) feltételek mellett a (7) célfüggvény optimalizálását jelenti, egy lineáris programozási probléma.
Valaki ajánlatot tesz a gyár tulajdonosának, hogy bérbe veszi az üzemet. Hogy létrejön-e az üzlet, még nem tudjuk, de egy dolog biztos: a tulajdonos vagy minden gépet bérbe ad vagy egyet sem. Az alku most akörül folyik, hogy az egyes gépek bérleti díja mennyi legyen. Tegyük fel, hogy az egyelőre még ismeretlen bérleti díjak az 1, 2, , gépek esetén időegységenként , , , .
A tulajdonosnak akkor éri meg bérbe adni az üzemet, ha olyan bérleti díjakat kap, hogy ezzel jobban jár, mintha akármelyik termékét gyártaná. Nézzük például az első terméket. Ennek egy egységén a haszon, és ennek legyártásához , , , egységnyi időket használ fel, melyekért rendre , , , bérleti díjakat kap. Tehát az utóbbiak összegének legalább akkorának kell lennie, mint . Hasonló igaz a többi gépre is. Innen az | | (8) |
feltételeket kapjuk. A változók most sem lehetnek negatívak, hiszen ez azt jelentené, hogy valamelyik gép kölcsönzéséért nemhogy nem kap a tulajdonos pénzt, hanem egyenesen neki kell fizetnie: (8) és (9) a bérbeadás feltétele. A bérlő nem tud a maga szempontjából jobb díjat elérni, mintha ezen feltételek mellett minimalizálja az összdíjat, azaz megkeresi a | | (10) |
célfüggvény optimális értékét, tehát neki akkor éri meg bérbevenni a gyárat, ha azt olyan ügyesen tudja felhasználni, hogy ennél nagyobb hasznot tud elérni.
A (8)‐(10) feladat ismét egy lineáris programozási feladat. Ezt nevezzük az (5)‐(7) feladat duáljának. Magának az (5)‐(7) problémának primál feladat a neve. Vegyük szemügyre a két feladatot formálisan. Az (5) egyenlőtlenségrendszer baloldán az együtthatókat soronként felírva az alábbi, úgynevezett mátrixot kapjuk: | | (11) |
Ebből úgy kapjuk meg a (8) feltételrendszer baloldalának mátrixát, hogy tükrözzük a főátlóra, azaz a bal felső sarokból induló azon ,,vonalra", amely azokból az együtthatókból áll, melyek két indexe egyenlő: | | (12) |
Ami a primál feladatban a célfüggvény volt, az a duáljában az egyenlőtlenségek jobboldala és viszont. Amikor az (5)‐(7) feladatot bevezettük, akkor az együttható jelentése az volt, hogy a termék egy egysége mennyi időt tölt az gépen. Természetes volna tehát azt gondolni, hogy az ilyen együtthatók nem lehetnek negatívak. Hasonló vonatkozik a , mennyiségekre is, hiszen például mi értelme volna egy olyan terméket gyártani, amin negatív nyereség, magyarul veszteség keletkezik. Mi azonban most eltekintünk ezektől a megfontolásoktól, és megengedjük, hogy a feladatokban szereplő mennyiségek tetszőleges valós számok legyenek. Még ebben az esetben is igaz azonban mind a gyenge, mind az erős dualitási tétel:
3. tétel: Tegyük fel, hogy az , , , értékek kielégítik az (5) és (6) feltételeket, hasonlóképpen az , , , értékek pedig a (8) és (9) egyenlőtlenségeket. Ekkor | | (13) |
Bizonyítás: Mivel az , , , nem lehetnek negatívak, ezért szabad velük az (5) egyenlőtlenségeket rendre beszorozni, majd az így kapott egyenlőtlenségeket összeadni. Így azt kapjuk, hogy | | (14) |
Ugyanígy beszorozhatjuk a (8) egyenlőtlenségeket rendre a , , , menyiségekkel és a keletkező egyenlőtlenségeket összegezhetjük: | | (15) |
Innen a kívánt egyenlőtlenség azért következik, mivel (14) és (15) baloldala megegyezik.
Köztudottl. pl.: Prékopa András: Lineáris programozás, KÖMAL, 1998/1. sz., hogy egy lineáris programozási feladat három osztályba eshet: (i) egyáltalán nincs megengedett megoldása, (ii) van megengedett megoldása, de a célfüggvénye nemkorlátos, azaz ha jelöli az , , , értékekből álló -est, akkor létezik megengedett megoldásoknak egy olyan , , végtelen sorozata, hogy , (iii) a feladatnak van optimális megoldása. A gyenge dualitási tételből következik, hogy amennyiben a primál feladat nemkorlátos, akkor a duál feladatnak nem lehet megengedett megoldása. Ha ugyanis volna, akkor a célfüggvény ehhez tartozó értéke köteles volna legalább akkora lenni, mint az előbb említett határértékbeli sorozat valamennyi tagja, az pedig lehetetlen. Az erős dualitási tétel csak a (iii) esetre vonatkozhat, és a következőt állítja:
4. tétel: Ha a primál feladatnak van optimális megoldása, akkor van optimális megoldása a duál feladatnak is, és a két feladat optimális célfüggvényértékei egyenlők.
A tétel bizonyítása túllépi a jelen dolgozat kereteit, ezért elhagyjuk.
A lineáris programozás dualitási tételeinek nagyon sok fontos speciális esete van. Ezek közül több anélkül bizonyítható, hogy hivatkozni kellene a lineáris programozásra. Egy ilyen, építő vállalatok, nagy berendézeseket (pl. hajó, vonat, daru) gyártó üzemek napi gyakorlatában használt feladatról lesz szó.
Egy ház építését vesszük példának. Ez számos különböző tevékenységből áll. Ezek közül egyeseknek meg kell előzni másokat. Nyilvánvaló, hogy az alapok kiásása megelőzi például a falak felhúzását, a vízvezetékek szerelését. A tevékenységek halmazát jelölje . Ha és két tevékenység, azaz , , akkor három eset lehetséges: (i) az tevékenységnek már be kell fejeződnie, amikor a tevékenységhez hozzákezdünk, másképpen kifejezve megelőzi -t, (ii) az és tevékenység nincs hatással egymásra, (iii) megelőzi -t.
Persze például az alapok kiásása és a vízvezeték szerelése között számos tevékenység van, amit szintén el kell végezni. Azt mondjuk, hogy az tevékenység közvetlenül megelőzi a -t, ha nincsen olyan tevékenység, amit megelőz, és ami viszont megelőzi -t. Jelölje azon rendezett párok halmazát, ahol közvetlenül megelőzi -t. Ekkor az előzmény, az ,,utózmány''. Célunk az, hogy a ház a lehető legrövidebb idő alatt elkészüljön. Ehhez természetesen ismerni kell az egyes tevékenységek elvégzéséhez szükséges időt, amit az tevékenység esetén jelöl.
1. példa: Különösen családi ház építésénél fordul elő, hogy az egész ház elkészítését részfeladatokra bontják fel, és a leendő tulajdonos mindig azt a már elvégezhető részfeladatot csináltatja meg, amire pénze van. Tekintsük most egy ilyen részfeladatot, nevezetesen a gáz bevezetését az utca alatt található csőből egy kisebb átmérőjű, föld alatt vezetett csövön keresztül a házba. Az egyszerűség kedvéért tegyük fel, hogy ez a részfeladat mindössze a következő tevékenységekből áll: előkészítés (), a cső elhelyezéséhez szükséges árok kiásása (), a cső szerelése (), szigetelés (), a cső leeresztése az árokba (), a vezeték bekötése (), a vezeték próbája (), az árok befedése (). Zárójelben mindenütt az a betű áll, amivel az alábbiakban az adott tevékenységre hivatkozunk. A tevékenységek elvégzéséhez szükséges időket, az egyes tevékenységek közvetlen előzményeit és az egyes tevékenységek megkezdésének ütemezését az alábbi táblázat foglalja össze. A tevékenységek ütemezését alább elemezzük.
Tegyük fel, hogy a tevékenységeket megkezdésük után megszakítás nélkül folyamatosan végezzük. Ütemezzük az tevékenységet a képzeletbeli 0 időpontra, így az 1 időpontban fejező-dik be. Ennél előbb sem , sem nem kezdődhet el. Ha mindkettőt valóban megkezdjük ekkor, úgy a 11, a 4 időpontban fejeződik be. A 4 időpontban azonnal hozzáfoghatunk a tevékenységhez, és az a 8 időpontban ér véget. Ekkor azonban a még hátralévő tevékenységek, azaz , , , , egyike sem kezdődhet el, mert mindegyiknek van egy-egy olyan előzménye, ami még nem készült el. Ez a helyzet a 11 időpontban változik, amikor elkészül, és így hozzáfoghatunk -hez. A továbbiakat a táblázatunk tartalmazza, amiből kiderül, hogy a teljes szereléshez 17 időegység szükséges.
A gyakorlatban egy ház felépítése vagy egy nagyobb szerelési munka sok száz vagy ezer tevékenységből állhat, és ennek a nyomonkövetése kézzel már igen nehézkes. Ezért célunk egy olyan módszer kifejlesztése, amely számítógéppel végezhető.
Az , , , tevékenységeket útnak mondjuk, ha , , , . Ha , , , út, és még az is teljesül, hogy , akkor az utat körnek nevezzük. Első megállapításunk éppen az, hogy tevékenységekből nem lehet kört alkotni. Hiszen ekkor -t nem lehet elkezdeni amíg -et be nem fejeztük, -at, amíg -t be nem fejeztük, és így tovább, egészen addig, hogy -et sem lehet elkezdeni addig, amíg nincs kész, azaz a tevékenységek körben várnának egymásra, semelyikhez sem lehetne hozzákezdeni.
Feltesszük továbbá, hogy létezik egy kezdeti tevékenység, egy első kapavágás, aminek minden más tevékenységet meg kell előznie, és egy befejező tevékenység, a kulcsátadás, aminek minden más tevékenységet követnie kell.
Ütemezni fogjuk a tevékenységek megkezdését. Az kezdeti tevékenységet a képzeletbeli 0 időpontra tesszük. Általában az tevékenység megkezdésének időpontját jelöli. Ha közvetlenül megelőzi -t, akkor megkezdését csak olyan időpontra lehet ütemezni megkezdéséhez viszonyítva, hogy legyen elegendő idő teljes elvégzésére. Így az alábbi feltételeket kapjuk: | | (17) |
Amikor a tevékenységhez hozzákezdünk a időpontban, akkor már minden más tevékenységnek be kellett fejeződnie. Tehát a ház a kulcsátadás befejezésével, a időpontban ér véget. Ez az érték nem más, mint az úgynevezett teljes átfutási idő, vagyis az az idő, ami az építés megkezdésétől annak teljes befejezéséig eltelik. Célunk tehát ennek minimalizálása. Így a célfüggvény lesz. A érték konstans, ezért elhagyható volna, hiszen az optimális megoldást nem befolyásolja, de a későbbiekben szükségünk lesz rá. Most egy minimalizálási feladatot fogalmaztunk meg, ami az eddigiek szerint a duális feladat. Meg kell adni tehát a primál feladatot is.
Tegyük fel, hogy egy, a fenti értelemben vett út, amely az , , , tevékenységekből áll. A út hosszának a mennyiséget nevezzük. A primál feladat a leghosszabb -ből -be vezető út megkeresése. Formálisan | | (19) |
5. tétel: Legyen egy tetszőleges ütemezés, amely eleget tesz a (16)‐(17) feltételeknek, pedig egy -ből -be vezető út. Ekkor
Bizonyítás: Mivel , ezért . Így a (17) feltételből következik, hogy , hiszen megelőzi -t. Hasonlóképpen megelőzi -at, ezért . A gondolatmenetet így folytatva kapjuk, hogy . Itt mindkét oldalhoz hozzáadva a mennyiséget, azonnal adódik a kívánt állítás.
Ez tehát a gyenge dualitási tétel. Az erős dualitási tétel bizonyítása azonnal megadja azt az eljárást, amivel az optimális ütemezést meg lehet határozni.
6. tétel: Létezik egy olyan út -ből -be és egy ütemezés, hogy .
Bizonyítás: Legyen egy tetszőleges ütemezés. Azt mondjuk, hogy az pár a ütemezés szerint kritikus, ha . Tegyük fel, hogy , , , a tevékenységeknek egy olyan sorozata, hogy az , , , párok mind kritikusak. Ezért | | (21) |
Az utat egy -ből -ba vezető kritikus útnak nevezzük.
Megadunk egy módszert, ami lépésenként szerkeszti meg az optimális ütemezést. Az eljárás feltételezi, hogy létezik a tevékenységeknek egy olyan halmaza, amelynek az kezdeti tevékenység eleme, és minden elemére teljesül, hogy létezik egy olyan -ből -ba vezető út, hogy az ebben az útban szereplő összes tevékenység eleme, és ez az út egyben szerint kritikus. A módszer minden egyes lépése kibővíti az halmazt egy további tevékenységgel.
Kezdetben az halmaz álljon egyedül az kezdeti tevékenységből, és (16) szerint legyen . Ekkor az halmazra a mondott követelmények teljesülnek. Jelölje most azokat a tevékenységeket, amelyek nem tartoznak bele az halmazba. Azt állítjuk, hogy a -beli tevékenységek között van olyan, amelynek minden előzménye az halmazban található. Ha ugyanis ez nem igaz, akkor minden -beli tevékenységnek létezik egy -beli előzménye. Válasszunk egy tetszőleges -beli tevékenységet. Tehát ennek van egy -beli előzménye. Hasonlóképpen az utóbbinak van egy -beli előzménye, és így folytathatjuk a sort a végtelenségig. Mivel azonban csak véges sok tevékenység van a halmazban, ezért ebben a sorozatban legalább egy tevékenység ismételten fellép. Ez azonban azt jelenti, hogy a fenti értelemben létezik egy kör, ami ellentmondás.
Legyen most már az a tevékenység, amelynek minden előzménye az halmazban található. Jelölje ezen előzmények halmazát. Legyen | | (22) |
Legyen egy olyan tevékenység, amire a (22) egyenlet jobboldalán maximumot kapunk. Ekkor , azaz az pár kritikus. Továbbá létezik -ből -ba vezető kritikus út. Legyen ez , , , . Ekkor , , , , egy -ből -be vezető kritikus út. (21) szerint | | (23) |
vagyis a tevékenységet arra az időpontra ütemeztük, amely megegyezik az -ből a -be vezető kritikus út hosszával.
Mindezen műveletek elvégzése után a tevékenység a halmazból átkerül az halmazba. Ez az eljárás nem folytatható akármeddig, mert elfogynak az halmazon kívüli tevékenységek, azaz végül maga a befejező tevékenység is az halmazba fog tartozni. Ekkor az -ből -be vezető kritikus út hossza lesz tehát, ami ekvivalens az állítással.
Könnyen ellenőrizhető, hogy a 1. példa számítási módszere azonos a bizonyításban közölt módszerrel. Egyes tevékenységek esetleg később is kezdhetők a számítottnál anélkül, hogy az átfutási idő meghosszabodna. Ilyen volt a példában a tevékenység. De evvel a módszerrel mindig a lehetséges legkorábbi kezdési időket kapjuk meg. A lehetséges legkésőbbi kezdési időket, amikor az átfutási idő még mindig minimális, akkor kapjuk, ha a módszert a befejező tevékenységből visszafelé haladva fordított irányban végezzük el.
Bonyolultabb problémák esetén egy primál feladathoz több különböző duális feladatot is be lehet vezetni. Az egyik leggyakrabban használt típust nevezik Lagrange duál feladatnak.
Ha a primál feladatot valamilyen oknál fogva nehéz megoldani, viszont a duál feladatot magát megoldani vagy egy megengedett megoldását megtalálni könnyű, akkor a duál feladat bevezetésével azt nyerjük, hogy kapunk egy könnyen számítható felső korlátot a primál feladat optimális célfüggvényértékére. Éppen ez a helyzet a hátizsák feladatA hátizsák feladatot tárgyalja a "Mit tegyünk a hátizsákba, hogyan váltsunk fel pénzt?" c. cikk a KÖMAL 1996/7. és 8. számában. esetében. Legyen , , , , , , , , , pozitív egész. Ekkor a hátizsák feladat | | (24) |
Legyen egy tetszőleges, rögzített nemnegatív valós szám. Tekintsük a | | (25) |
feladatot. Az utóbbi feladat optimális célfüggvényértéke mindig legalább akkora, mint a hátizsák feladaté, ugyanis | |
Ha az , , , értékek kielégítik a hátizsák feladat feltételeit, akkor itt az egyenlőség jobboldalának második tagja két nemnegatív szám szorzata, tehát a teljes kifejezés legalább akkora, mint , vagyis a hátizsák feladat célfüggvényének értéke az , , , értékek mellett.
A (25) feladatot nagyon egyszerű megoldani, mivel a változók nincsenek közvetlen hatással egymásra, ezért mindegyik értéke úgy választható meg a többitől függetlenül, hogy az a célfüggvény szempontjából a lehető legjobb legyen, vagyis az optimális megoldást a következő képlet adja: | | (26) |
Ez vezet oda, hogy más esetekben is érdemes lehet valamely primál feladat helyett a (25) feladat megfelelő változatát megoldani. Most ezt megfogalmazzuk általánosan.
Legyen és pozitív egész. Az és , , , legyenek az , , , változók valós függvényei. Az halmaz elemei legyenek rendezett szám -esek. Végül legyen , , , rögzített valós szám. Primál feladatunk a következő: | | (27) |
Mind a lineáris programozási, mind a hátizsák feladat szerkezete beleillik ebbe az általános keretbe. A lineáris programozási feladat esetén az halmaz az összes nemnegatív komponensekből álló szám -es volt. A hátizsák feladatnál pedig az összes olyan, amelyben csak 0 és 1 szerepel. (Az, hogy rendezett szám -eseket tartalmaz, a következő példával magyarázható el. Tegyük fel, hogy , és de . Ekkor az , , értékek a feladat egy megengedett megoldását adják, feltéve, hogy ezeket behelyettesítve az egyenlőtlenségekbe, azokat kielégítik. Azonban az , , értékek akkor sem adnak megengedett megoldást, ha velük az egyenlőtlenségek teljesülnek, mivel ez az értékrendszer nincs benne az halmazban, vagyis amikor , akkor nem lehet és egyidejűleg .)
7. tétel: Legyen , , , rögzített valós szám. Ekkor | | (28) |
Megjegyzés: A tétel azt állítja, hogy a primál feladat optimális célfüggvényértéke nem lehet nagyobb, mint egy másik feladaté, amiben az egyetlen feltétel az, hogy szám -es az halmaz eleme. A , , , mennyiségek a Lagrange-szorzók, a jobboldali feladat pedig a (rögzített szorzók melletti) Lagrange-feladat.
Bizonyítás: Ha az , , , értékek kielégítik a primál feladat feltételeit, akkor a jobboldali feladat célfüggvényének második tagja nem lehet negatív, tehát ennek értéke legalább akkora, mint a primál feladat célfüggvényéé.
Innen a következő, úgynevezett Lagrange-duál feladatot lehet kitűzni: | | (29) |
A , , , számokat szokás Lagrange-szorzóknak nevezni. A 7. tétel szerint ez a feladat kielégíti azt a követelményt, amit egy duál feladatnak kell. Így a tétel maga nem volt más, mint a gyenge dualitási tétel. A (29) feladat tulajdonképpen az adott módszerrel megkapható legpontosabb, azaz legkisebb, tehát a legjobb felső korlátot határozza meg.
Itt azonban az erős dualitási tétel már nem igaz. Erre példa az alábbi feladat. | |
Mivel mindhárom változó külön-külön csak két értéket vehet fel, ezért összesen nyolc eset lehetséges. Ebből a nyolcból az első egyenlőtlenség csak azt az esetet zárja ki, amikor mindhárom változó 1, a második meg csak azt, amikor , . Innen könnyen látható, hogy az optimális megoldás , , . Az ehhez tartozó célfüggvényérték 9. A megfelelő Lagrange-feladat rögzített és mellett | | (30) |
Itt és valamilyen nemnegatív számok. Ezért a célfüggvényben együtthatója biztosan nagyobb, mint -é. Ezért a Lagrange-feladatnak semmilyen és sem lehet olyan optimális megoldása, amelyben és . Így összesen hat különböző optimális megoldás lehetséges. Ezeket egyenként végigvizsgálva látható, hogy a feladat célfüggvénye soha nem kisebb, mint 10, azaz fellép a dualitási gyepű. Mi most a hat lehetséges eset közül azt vizsgáljuk meg, amikor . Ekkor | |
Az első egyenlőtlenség következik a másodikból, így ezzel külön nem kell foglalkozni. Az értékek helyére behelyettesítve 1-et, a célfüggvény értéke lesz. Tehát ahhoz, hogy a célfüggvény a lehető legkisebb legyen, -et a lehető legnagyobbra kell választani. Azonban a második és harmadik egyenlőtlenséget összeadva és egyszerűsítve azt kapjuk, hogy . Tehát ebben az esetben a célfüggvény értéke legalább 10. Hasonlóan elemezhető a további öt eset. Mindig azt kapjuk, hogy a Lagrange-feladat optimális célfüggvényértéke legalább 10. Tehát a Lagrange-duál feladatéé is, amely nem más, mint megkeresni és azon értékét, amire a (30) feladat optimális célfüggvényértéke minimális.
Megjegyezzük, hogy egyes esetekben, például amikor a (27) probléma egy lineáris programozási feladat, igaz az erős dualitási tétel is.
Vizvári Béla Eötvös Loránd Tudományegyetem, Operációkutatási Tanszék
*** |
|
PDF | MathML 
