A minden irányú elfordulást megengedő csuklókkal összekapcsolt merev rudakat rúd-csukló szerkezetnek nevezzük. Egy rúd-csukló szerkezet merev, ha bármely két csukló (nemcsak a rudakkal összekötöttek) távolsága állandó marad a szerkezet csuklóinak bármely folytonos mozgatása során. Például egy ,,négyzet'' nem merev a síkban, mert ,,rombusszá'' deformálható. Ha egyik átlójával bővítjük a négyzetet, akkor a síkban egy merev szerkezetet kapunk.
A merevségi vizsgálatoknál a dimenzió is fontos tényező, hiszen az átlójával bővített négyzet a síkban merev, de a térben nem, ugyanis az átló körül az átlón kívüli csúcsok egymástól függetlenül elfordulhatnak.
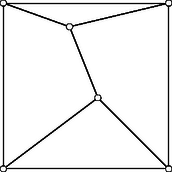
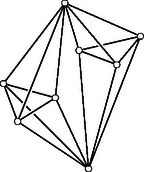
Egy $c$ darab csuklót tartalmazó szerkezet merevségének szükséges feltétele, hogy a rudak $r$ száma legalább $2c-3$ legyen a síkban, és legalább $3c-6$ a térben. A síkban vegyünk egy háromszöget, amelynek oldalai a szerkezet rúdjainak, csúcsai pedig a szerkezet csuklóinak felelnek meg. Ez a szerkezet merev, és természetesen kielégíti a szükséges feltételt. Egy merev szerkezethez mereven csatlakoztathatunk egy újabb csuklót legalább két rúddal, így a szerkezet rúdjainak száma legalább 2-vel nő minden újabb csukló hozzávételével, tehát a szükséges feltétel érvényben marad. Hasonlóan támaszthatjuk alá a szükséges feltételt térben is. Ez a meggondolás azonban nem bizonyító erejű, hiszen az említett iterációval nem juthatunk el minden merev szerkezethez, például az 1. ábrán látható szerkezethez sem. A szükséges feltétel korrekt bizonyítása megtalálható a cikk végén említett könyvben.
Ha egy szerkezet merev, és rúdjainak száma a síkban több, mint $2c-3$, illetve térben több, mint $3c-6$, akkor található olyan rúd, amelyet elhagyva a szerkezetből, az továbbra is merev marad. Azokat a merev szerkezeteket, amelyekből már nem hagyható el további rúd úgy, hogy a szerkezet még merev maradjon, minimális merev szerkezeteknek nevezzük. Természetesen a minimális merev szerkezetekben az élszám $2c-3$ a síban, illetve $3c-6$ a térben. A továbbiakban csak ilyen minimális merev szerkezetekkel foglalkozunk, és csak a síkban,
Tekintsünk olyan síkbeli szerkezeteket, amelyeknek rúdjai és csuklói kölcsönösen egyértelműen megfeleltethetők egy térbeli konvex poliéder éleinek és csúcsainak. A síkbeli szerkezetnek így megfeleltetett térbeli poliédereket nevezzük megfelelő konvex poliédereknek. A következő meglepő állítás kapcsolatot teremt síkbeli minimális szerkezetek merevsége és térbeli konvex poliéderek élhálózatának síkbeli vetülete között.
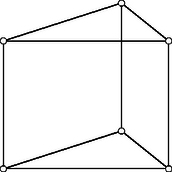
Egy minimális síkbeli szerkezet akkor és csak akkor merev, ha a szerkezet rajza nem állítható elő egy térbeli megfelelő konvex poliéder élhálózatának vetületeként. Az 1. ábrán látható szerkezet rajza nem állítható elő mint egy térbeli konvex poliéder síkbeli vetülete, mivel egyébként a háromszögek közelebbi csuklóit összekötő rúdnak megfelelő poliéderél egyenese a másik négy csúcshoz tartozó lapot két pontban is metszené. A 2. ábrán található szerkezet rajza viszont egy háromszög alapú hasáb vetületeként előáll, ezért ez a szerkezet nem merev.
Az előző tételt használva egy szerkezet merevségének igazolásához meg kell mutatnunk, hogy nincs olyan konvex poliéder, amely élhálózatának vetülete az adott szerkezet rajzával azonos lenne. Ez általában nem könnyű probléma.
Feleltessünk meg egy szerkezetnek egy gráfot úgy, hogy a gráf csúcsai felelnek meg a szerkezet csuklóinak, és két csúcs között akkor és csak akkor van él, ha a szerkezet megfelelő csuklói között van rúd. Így minden szerkezethez tartozik egy gráf, de egy gráfhoz több szerkezet is tartozhat. Ezek között lehetnek merevek és nem merevek is, ilyen szerkezetet látunk az 1. és a 2. ábrán. Nyilvánvalóan a két szerkezet gráfja azonos, azonban az 1. ábrán látható szerkezet merev, a 2. ábrán látható nem. Ha a 2. ábrán látható szerkezet rúdjainak hosszát ,,kissé'' megváltoztatjuk, akkor merev szerkezethez jutunk. Nevezzük ezért az ilyen tulajdonságú szerkezeteket generikusan merevnek.
Ha egy gráfnak megfelelő valamely szerkezet generikusan merev, akkor a gráfnak megfelelő összes generikus szerkezet generikusan merev lesz. Egy gráf akkor merev, ha van legalább egy megfelelő generikusan merev szerkezete. Ezért az 1. és a 2. ábrán látható szerkezetek gráfja merev.
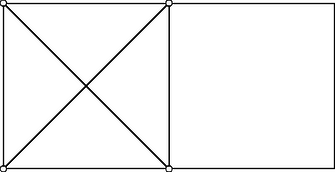
G. Laman talált először szükséges és elégséges feltételt gráfok síkbeli merevségére. Egy $2c-3$ élt tartalmazó gráf akkor és csak akkor merev, ha bármely részgráfja legfeljebb $2c\text{'}-3$ élt tartalmaz, ahol $c\text{'}$ a részgráf csúcsainak számát jelöli. Előző gráfunkról tehát eldönthetjük, hogy merev-e, ha ellenőrizzük, hogy a részgráfokban nincs-e több él, mint $2c\text{'}-3$. Nevezzük ezt Laman-féle feltételnek. A 3. ábrán egy olyan szerkezetet látunk, amelyhez tartozó gráf egy részgráfjában, nevezetesen a bal oldali négy csuklónak és a köztük levő rudaknak megfelelő részgráfjában, a Laman-féle feltétel nem teljesül, ezért ez a gráf nem merev, és a szerkezet sem merev. Annak eldöntése, hogy a gráf merev-e, exponenciális számú lépést igényelne a Laman-féle feltétel alkalmazásával, hiszen minden részgráfot meg kell vizsgálnunk.
Lovász László és Y. Yemini ereménye polinomiális számú lépésben tudja eldönteni egy gráfról a síkbeli merevséget. A tétel megértéséhez szükséges a következő definíció: Egy összefüggő gráf feszítőfája egy olyan fa gráf, amelynek csúcsai megegyeznek a gráf csúcsaival, élei pedig a gráf élei közül valók. Lovász és Yemini tétele:
Egy $2c-3$ élt tartalmazó gráf akkor és csak akkor merev, ha bármely élét megduplázva az így kapott gráfnak van két feszítőfája, amelyek közös élt nem tartalmaznak.
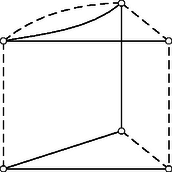
Az 1. és a 2. ábrán látható szerkezetek gráfjának egy élét megduplázva kapjuk a 4. ábrán látható két, közös élt nem tartalmazó feszítőfát.
A térben a $3v-6$ pontú merev gráfokra teljesül, hogy a részgráfok legfeljebb $3v\text{'}-6$ élt tartalmaznak, viszont a megfordítás már nem. Az 5. ábrán látható térbeli szerkezet rendelkezik a szükséges feltételekkel, de a szerkezet nem merev, ugyanis a két banánszerű szerkezet egymástól függetlenül az érintési pontjaik által meghatározott egyenes körül szabadon foroghat. Térbeli szerkezetek gráfjaira a merevség jól ellenőrizhető jellemzése még nyitott probléma. A térbeli szerkezetek merevségének tárgyalása szintén megtalálható a cikk végén található irodalomban.
A. L. Cauchy mondott ki konvex poliéderekre merevséggel kapcsolatos tételt. Tekintsük a poliéder lapjait merev lemezeknek, és azokat az éleik mentén zsanérszerűen rögzítve képzeljük el a poliédert. Ha a poliéder lapjai merevek, és a poliéder konvex, akkor a poliéder merev.
Rúd-csukló szerkezetként előállíva egy konvex poliédert, a lapok merevségét csak háromszöglapok esetén garantálhatjuk. Ezért Cauchy tétele rúd-csukló szerkezetekre átfogalmazva a következő lenne:
A háromszöglapú konvex poliéderek, mint rúd-csukló szerkezetek, merevek a térben.
Évszázados probléma volt, hogy a konvexitás feltétele elhagyható-e Cauchy tételében. Sokáig és sokan azt hitték, hogy a konvexség feltétele elhagyható, de a válasz nemleges. R. Conelly talált először olyan poliédert, amely nem konvex és nem merev. Ilyen poliédert láthatunk a hátsó borító ábráján. Ez egy olyan háromszöglapú test, amelynek csúcsaiba csuklókat, éleire rudakat helyezve egy nem merev szerkezethez jutunk. Az ábra két szélén levő gúla-szerű szerkezetek hosszú nyíllal jelölt csúcsait egyesítve a szerkezet szívószálakon átbújtatott cérnák segítségével elkészíthető, ha van hozzá türelmünk és kitartásunk. Az azonosan jelölet rudak hosszát a keretezett számok jelölik. A szaggatott nyíl irányában a felső csúcs mozgatható.
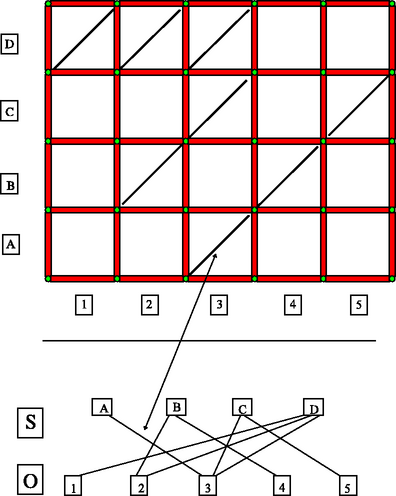
A generikus szerkezetekkel ellentétben vizsgálhatunk olyan szerkezeteket is, amelyek nagyszámú, azonos hosszúságú rúdból állnak. Ilyenek például a rácsszerű szerkezetek. A síkbeli rácsszerű szerkezetek közül az $n\times m$-es négyzetrácsokkal foglalkozunk részletesebben. Természetesen ezek nem merevek a síkban, merevítésükhöz további rudakra van szükség. Merevségen most nem a generikus merevséget, hanem az eredeti definíció szerintit értjük, hiszen azt szeretnénk most kihasználni, hogy a csuklók és a rudak helyzete speciális. A merevítéshez szükséges további rudakat a négyzetek átlóiba tesszük, és átlós merevítőnek nevezzük. Készítsük el egy átlós merevítőket tartalmazó négyzetrács szerkezet merevítés-gráfját, ez egy páros gráf lesz, amelynek két pontosztályát $S$-sel és $O$-val jelöljük. A négyzetrács sorai feleljenek meg az $S$ osztálynak, oszlopai az $O$ osztálynak; ha van átlós merevítő az $i$-edik sor $j$-edik oszlopában, akkor legyen él az $i$ és $j$ pontok között a merevítés-gráfban (6. ábra).
Négyzetrácsok átlós merevítésére ad szükséges és elégséges feltételt E. D. Bolker és H. Crapo következő tétele:
Átlóival merevített négyzetrács szerkezet a síkban akkor és csak akkor merev, ha a merevítés-gráfja összefüggő.
Ennek a tételnek a segítségével a merevítés-gráf ismeretében lineáris időben eldönthető, hogy a négyzetrács szerkezet merev-e. Hasonló tétel kockarácsra térben nem ismert.