Cím:	1997. évi Kürschák József Matemetikai Tanulóverseny feladatainak megoldása
Szerző(k):	Kós Géza ,  Surányi János ,  Újváry-Menyhárt Zoltán
Füzet:	1998/február, 66 - 72. oldal	PDF  |  MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   1. Legyen $p$ páratlan prímszám, és tekintsük a síkon azokat a pontokat, amelyeknek mindkét koordinátája a $0$, $1$, $2$, $\text{...}$, $p-1$ számok valamelyike. Mutassuk meg, hogy ezen rácspontok közül kiválasztható $p$ darab, amelyek közül semelyik három nem esik egy egyenesre.   Megoldás. Bebizonyítjuk, hogy azok az $A:\left(i\mathrm{,}y\left(i\right)\right)$ pontok, amelyeknél $y\left(x\right)$ az $x^2$ (legkisebb nemnegatív) maradéka $p$-vel történő osztásnál ($0\le i\le p-1$), kielégítik a követelményt. Az értelmezés szerint $y\left(x\right)=x^2+cp$ alkalmas $c$ egésszel. Tegyük fel, hogy az $A_i{A}_j$ és az $A_i{A}_k$ szakaszok meredeksége egyenlő volna: $\begin{array}{c}{\displaystyle \frac{y\left(j\right)-y\left(i\right)}{j-i}=\frac{y\left(k\right)-y\left(i\right)}{k-i}\mathrm{.}}\end{array}$ A törteket eltávolítva, az értelmezést felhasználva és átrendezve: $\begin{array}{c}{\displaystyle \left(k-i\right)\left(j^2-i^2+\left(v-u\right)p\right)=\left(j-i\right)\left(k^2-i^2+\left(w-u\right)p\right)\mathrm{,}}\end{array}$ továbbrendezve és alakítva $\begin{array}{c}{\displaystyle \left(k-i\right)\left(j-i\right)\left(j-k\right)=p\left(\left(j-i\right)\left(w-u\right)-\left(k-i\right)\left(v-u\right)\right)\mathrm{.}}\end{array}$ A bal oldali szorzatnak kellene tehát oszthatónak lennie $p$-vel. Ez azonban nem lehetséges, mert egy szorzat csak úgy lehet osztható egy prímszámmal, ha valamelyik tényezője osztható vele, itt pedig mindegyik tényező 0-tól különböző és abszolút értékük $p$-nél kisebb. Nem lehet tehát a két meredekség egyenlő.   Megjegyzések. 1. Az $x^2$ helyett bármilyen egész együtthatós vagy egész helyeken egész értéket felvevő, másodfokú polinom megfelel. Érdekes, hogy a feladattal foglalkozó versenyzők többnyire az $\frac{x\left(x+1\right)}{2}$ polinomot választották. 2. Többen használtak olyan pontatlan állításokat, mint különbség maradéka egyenlő a maradékok különbségével, vagy szorzat maradéka egyenlő a tényezők maradékainak szorzatával, amelyek csak kiegészítésekkel érvényesek. 3. Egy versenyző azokat az $\left(x\mathrm{,}y\right)$ pontokat adta meg, amelyekre $xy\equiv 1$ (mod $p$) ($1\le x\le p-1$), maga is megjegyezve, hogy így csak $p-1$ pontot kap. 4. A kérdésnek kiterjedt irodalma van. A feladat állítása igaznak látszik prímszám helyett minden pozitív egész számra, sőt próbálgatások során $n=32$-ig és számos nagyobb páros $n$-re $2n$ pontot is sikerült találni úgy, hogy ne legyen közülük 3 egy egyenesen. Sikerült bebizonyítani, hogy tetszés szerinti pozitív $h$ értékhez $\left(3/2\right)-h)n$ pont is kiválasztható, ha $n$ elég nagy. 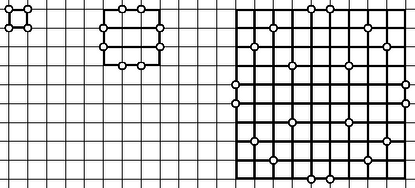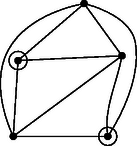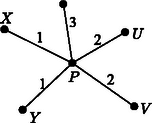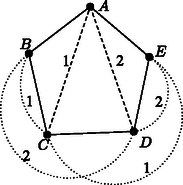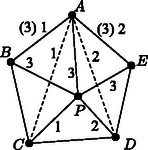A problémával kapcsolatban R. K. Guy és P. A. Kelly több érdekes sejtést fogalmazott meg. Így többek közt azt sejtik, hogy csak az 1. ábrán látható 3 esetben helyezhető el $2n$ pont egy $n$ oldalhosszú négyzetben úgy, hogy rendelkezzék a négyzet összes szimmetriájával; azt sejtik továbbá, hogy nagy $n$-re legfeljebb $\left(c+h\right)n$ pont helyezhető el a követelménynek megfelelően, ahol $c={\left(2{\pi }^2/3\right)}^{1/3}\approx 1\mathrm{,}85$. ${}^{*}$R. K. Guy: Unsolved problems in number theory, 2. kiad. Springer, 1996. XVI + 285 old., közelebbről 242‐244. old.   1. ábra     2. 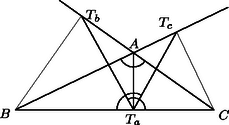Az $ABC$ háromszög körülírt körének középpontja $O$. A beírt kör az oldalakat az $A_1$, $B_1$, $C_1$ pontokban érinti, középpontja $O_1$. Az $A_1{B}_1{C}_1$ háromszög magasságpontja $M_1$. Igazoljuk, hogy az $O$, $O_1$, $M_1$ pontok egy egyenesen vannak.   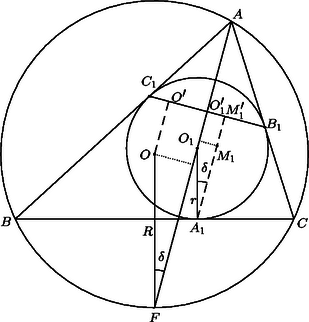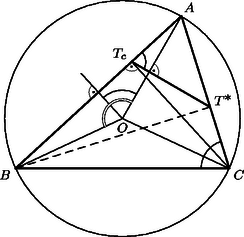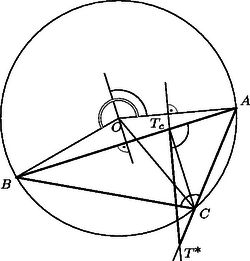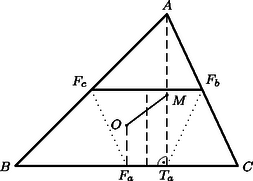I. megoldás. Tekintsük az $O$, $O_1$ és $M_1$ pontok merőleges vetületeit az $A_1{B}_1{C}_1$ háromszög oldalaira. Elegendő azt megmutatni, hogy az ezek közti szakaszok aránya két különböző oldalon megegyező. Határozzuk meg ezt az arányt pl. a $B_1{C}_1$ oldalon. $F$-fel jelölve az $ABC$ háromszög köré írt kör $A$-t nem tartalmazó $BC$ ívének felezőpontját, ezen átmegy az $O$-ból a $BC$ oldalra emelt merőleges is és az $A$-ból induló szögfelező is. Jelöljük a köztük levő szöget $\delta$-val (2. ábra). Az $O_1{A}_1$ érintési sugár szintén merőleges a $BC$ oldalra.   2. ábra   $O$, $O_1$ és $M_1$ merőleges vetületét a $B_1{C}_1$ oldalon jelöljük $O\text{'}$, $O_1\text{'}$ és $M_1\text{'}$-vel. Az $A{B}_1{C}_1$ háromszög egyenlő szárú, ezért $O_1\text{'}$ $AF$-en van, tehát $A_1{M}_1$ párhuzamos $AF$-fel, és így $O_1{A}_1{M}_1\sphericalangle =\delta$. Az $O$-ból $AF$-re és $O_1$-ből $A_1{M}_1\text{'}$-re emelt merőleges szakaszok az $O\text{'}{O}_1\text{'}$, illetőleg $O_1\text{'}{M}_1\text{'}$ szakasszal egyenlők, tehát hosszuk $R\text{sin}\delta$, illetőleg $r\text{sin}\delta$, ahol $R$ a háromszög köré írt kör sugara, $r$ a beírt köré. Így $\begin{array}{c}{\displaystyle O\text{'}{O}_1\text{'}:O_1\text{'}{M}_1\text{'}=\left(R\text{sin}\delta \right):\left(r\text{sin}\delta \right)=R:r\mathrm{.}}\end{array}$ Ez az arány azonban csak a két kör adataitól függ, a $B_1{C}_1$ oldaltól nem, így ugyanez az arány adódik a másik két oldalon levő vetületek közti szakaszokra is. Ezzel a feladat állítása bizonyítást nyert.   II. megoldás. A megoldáshoz felhasználunk a háromszögekre vonatkozó néhány összefüggést, amelyeket a megoldás végén bizonyítunk. 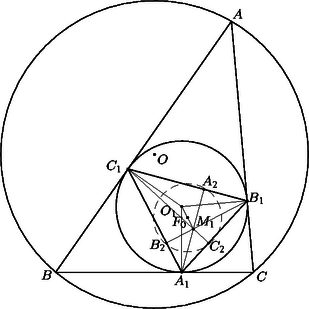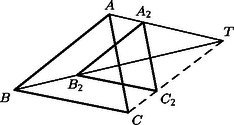Jelöljük az $A_1{B}_1{C}_1$ háromszög csúcsaiból húzott magasságok talppontját rendre $A_2$, $B_2$, $C_2$-vel (3. ábra).   3. ábra   a) Egy háromszög magasságai felezik a talpponti háromszög szögeit, így a magasságpont a talpponti háromszögbe írt kör középpontja, esetünkben $M_1$ az $A_2{B}_2{C}_2$-be írté. b) Ismeretes, hogy a háromszög (esetünkben az $A_1{B}_1{C}_1$ háromszög) köré írt körnek a csúcsokhoz mutató sugarai merőlegesek a talpponti háromszög oldalaira. Esetünkben $O_1{A}_1$, $O_1{B}_1$, $O_1{C}_1$ érintési sugár is, tehát merőleges rendre a $BC$, $CA$, $AB$ oldalra is, tehát az $ABC$ és az $A_2{B}_2{C}_2$ háromszög oldalai párhuzamosak. c) A két háromszög hasonló helyzetű is, s így rájuk vonatkozóan megfelelő pontpárok összekötő egyenesei is párhuzamosak. d) Az $A_2{B}_2{C}_2$ háromszög köré írt kör az $A_1{B}_1{C}_1$ háromszög ún. Feuerbach-köre, ez átmegy az oldalak felezőpontjain is, és középpontja az $O_1{M}_1$ szakasz $F_0$ felezőpontja. Az $ABC$ háromszögre vonatkozóan $O$ és $O_1$ megfelelői az $A_2{B}_2{C}_2$-re vonatkozóan $F_0$ és $M_1$, így összekötő egyeneseik párhuzamosak. A két egyenesnek azonban $O_1$ közös pontja, így $O$, $O_1$ és $M_1$ egy egyenesen van, és ezt kellett bizonyítani.   Bebizonyítjuk a felhasznált összefüggéseket.     4. 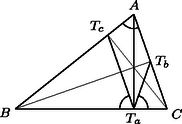ábra   a) Jelöljük az $ABC$ háromszög egymás utáni csúcsaiból húzott magasságainak talppontját $T_a$, $T_b$, $T_c$-vel (4. ábra). Az $AB{T}_a{T}_b$ és az $AC{T}_a{T}_c$ négyszög húrnégyszög, így $T_c{T}_{a}B\sphericalangle =CAB\sphericalangle$ és $T_b{T}_{a}C\sphericalangle =BAC\sphericalangle$, tehát $A{T}_a$ szögfelező.     5. ábra   b) Az $ABC$ háromszög köré írt $O$ középpontú körben az $AOB\sphericalangle$ mint középponti szög az $ACB\sphericalangle$ kétszerese (5. ábra). Szögfelezője merőleges $AB$-re, és $ACB\sphericalangle$ nagyságú szöget zár be vele. A $C$ pontból húzott magasság $T_c$ talppontjából állítsunk merőlegest $OA$-ra, messe ez a $CA$ oldal egyenesét a $T^{*}$ pontban. Ekkor $A{T}_c{T}^{*}\sphericalangle$ mint merőleges szárú szög ugyancsak $ACB\sphericalangle$ nagyságú, tehát $BC{T}^{*}{T}_C$ húrnégyszög, benne a $BC$ oldal $T_C$-ből derékszögben látszik, tehát $T^{*}$-ból is, vagyis $T^{*}$ a $B$-ből húzott magasság talppontja, $T_b$. c) Azt kell belátnunk, hogy ha az $ABC$ és az $A_2{B}_2{C}_2$ háromszög megfelelő oldalai párhuzamosak, akkor $A{A}_2$, $B{B}_2$ és $C{C}_2$ egy ponton megy keresztül, vagy párhuzamosak (6. ábra).   6. ábra   Ha pl. $A{A}_2$ és $B{B}_2$ metszi egymást egy $T$ pontban, akkor $ABT$ és $A_2{B}_{2}T$ hasonló háromszögek, így $AT:A_{2}T=AB:A_2{B}_2=BT:B_{2}T$. Másrészt $AB:A_2{B}_2=BC=B_2{C}_2$. Ekkor azonban a $BCT$ és a $B_2{C}_{2}T$ háromszög is hasonló, mert egy szögük és az azt közrefogó oldalak aránya egyenlő. Ebből viszont következik, hogy $C$, $C_2$ és $T$ is egy egyenesen van. d) A Feuerbach-körre vonatkozó állítások igazolására jelöljük a $BC$, $CA$, $AB$ oldalak felezőpontjait rendre $F_a$, $F_b$, $F_c$-vel (7. ábra(.   7. ábra   Az $A$ csúcs tükörképe az $F_b{F}_c$ középvonalra a $T_a$ magasságtalppont. $F_a{F}_c$ mint középvonal $F_{b}A$-val egyenlő és párhuzamos, a tükrözés folytán pedig $F_b{T}_a$-val egyenlő. Így $F_a{T}_a{F}_b{F}_c$ szimmetrikus trapéz (lehet hurkolt, esetleg egyenlő szárú háromszög). Így kör írható köré, amelynek középpontja az $F_a{T}_a$ szakasz felezőmerőlegesén van, az pedig felezi az $O$ és az $M$ magasságpont közti szakaszt. A kör átmegy mind a három oldal felezőpontján, így a gondolatot a másik két oldalra megismételve, ugyanaz a kör adódik, sőt, azt is kapjuk, hogy a kör középpontja az $OM$ szakasz $F_0$ felezőpontja. Az oldafelezőpontok és a magasságtalppontok közül bármelyik 3 különböző már meghatározza a kört.   3. Bizonyítsuk be, hogy tetszőleges síkba rajzolható gráf élei kiszínezhetők három színnel úgy, hogy a gráfban ne legyen egyszínű kör.   Megoldás. A feladat állítását hurokél és többszörös él nélküli gráfokra, ún. egyszerű gráfokra bizonyítjuk. (Hurokél minden színezésnél egyszínű körhöz vezetne, és egy négy éllel összekötött pontpár esetén már szintén keletkeznék kör.) Szükségünk lesz a síkra rajzolható gráfok két ismert tulajdonságára (ezek bizonyításával kapcsolatban lásd megjegyzéseinket): * 1) Síkra rajzolható gráfban nem lehet teljes ötszög, azaz öt olyan pont, amelyek közül bármely kettőt él köt össze. * 2) Tetszőleges síkra rajzolható gráf tartalmaz legfeljebb 5-ödfokú pontot, azaz olyan pontot, amelyből legfeljebb 5 él indul ki. Az állítást a pontok száma szerinti indukcióval bizonyítjuk. 1, 2 és 3 pontú gráfokra az állítás triviális. Tegyük fel, hogy az állítás igaz $n$ csúcsú gráfokra, és tekintsünk egy tetszőleges $n+1$ csúcsú síkra rajzolható gráfot. Ennek létezik legfeljebb 5-ödfokú pontja, legyen $P$ egy ilyen pont. A $P$ pont foka szerint három esetet különböztetünk meg. I. eset: $P$ legfeljebb 3-adfokú. Hagyjuk el $P$-t a belőle induló élekkel együtt. A megmaradó $G\text{'}$ gráf továbbra is síkra rajzolható, és az indukciós feltétel szerint jól színezhető, azaz nem lesz benne egyszínű kör. Ezután $G\text{'}$ egy jó színezéséhez a $P$-ből induló éleket színezzük különbözőre. Egyszínű kör $G\text{'}$-ben nincs, és a $P$-n átmenő körök is tartalmaznak két $P$-ből induló, különböző színű élt, a kapott színezés tehát jó. II. eset: $P$ 4-edfokú. Legyenek a $P$-vel összekötött pontok $A$, $B$, $C$ és $D$. Ezek között van kettő ‐ mondjuk $A$ és $B$ ‐, amelyek között nincs él, mert $P$-vel együtt nem alkothatnak teljes ötszöget. Hagyjuk el a $P$ pontot a belőle kiinduló élekkel együtt, és húzzuk be az $AB$ élt (Ez lehetséges, pl. az eredeti $AP$, $PB$ élekhez elég közel, (ld. 8. ábra).   8. ábra   A keletkező $G\text{'}$ gráfot színezzük jól. Tegyük fel, hogy az $AB$ él az $1$-es színt kapta. Ezután színezzük $G$-ben az $AP$, $PB$ éleket az $1$-es színnel, $PC$-t és $PD$-t pedig a $2$-es és a $3$-as színnel. A $G\text{'}$ jó színezése miatt egyszínű kör csak $P$-n keresztül haladhatna, és csak a $P$-ből kiinduló két egyszínű élen, $AP$-n és $PB$-n keresztül. Akkor azonban $G\text{'}$ is tartalmazna $1$-es színű kört az $AB$ élen keresztül. III. eset: $P$ ötödfokú. Legyenek a $P$-ből kiinduló élek a körüljárás sorrendjében $PA$, $PB$, $PC$, $PD$ és $PE$. Ha az $AB$, $BC$, $CD$, $DE$ és $EA$ élek valamelyike nem szerepelne $G$-ben, akkor húzzuk be. (Ez lehetséges, mert például ha $AB$ nem szerepel, akkor az $A$ és $B$ pontokat összeköthetjük az $AP$ és $PB$ élekhez elég közel.) Ha ezt a bővített gráfot jól színezzük, az az eredeti gráfnak is egy jó színezését adja. A továbbiakban feltehetjük tehát, hogy az $AB$, $BC$, $CD$, $DE$ és $EA$ élek szerepelnek a gráfban. Ezután megmutatjuk, hogy a $P$ és a belőle induló élek elhagyása után az $ABCDE$ ötszögnek meghúzható két, egy csúcsból induló átlója. Ha egyik átló sem szerepel $G$-ben, akkor behúzhatjuk $AC$-t és $AD$-t az $AP$ és $PC$, illetve $AP$ és $PD$ élekhez elég közel. Az új élek csak a $PB$ és $PE$ élt metszik, így a keletkező $G\text{'}$ gráf síkra rajzolható. Ha például a $BE$ él szerepel $G$-ben, akkor a $BEP$ háromszög elválasztja $A$-t $C$-től és $D$-től, így $G$-ben nem szerepelhet sem az $AC$, sem az $AD$ él. Húzzuk meg ezeket az előbbi módon, majd hagyjuk el $P$-t a belőle induló élekkel együtt, így most is síkra rajzolható $G\text{'}$ gráfot kapunk. Az indukciós feltevés szerint $G\text{'}$ jól színezhető (9. ábra).   9. ábra   Színezzük jól a $G\text{'}$ gráfot. Ha a színezésben $AC$ és $AD$ ugyanolyan, mondjuk $1$-es színű, akkor $G$-nek a $G\text{'}$-ben is szereplő élei színét megtartva színezzük az $AP$, $CP$ és $DP$ éleket $1$-es színnel, a $BP$ és $EP$ éleket $2$-es, illetve $3$-as színnel (10. ábra).   10. ábra   Ha az így kapott gráfban van egyszínű kör, akkor az ismét csak $1$-es színű lehet, $P$-n keresztül halad az $AP$ és $PC$, az $AP$ és $PD$ vagy pedig a $CP$ és $PD$ éleken keresztül. Ezekben az esetekben viszont $G\text{'}$ is tartalmaz egyszínű kört az $AC$, az $AD$, illetve a $CA$ és $AD$ éleken keresztül. A továbbiakban ezért feltesszük, hogy $AC$ és $AD$ színe különböző: $1$-es, illetve $2$-es. 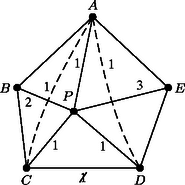Hagyjuk el az $AC$ és $AD$ átlókat, és vizsgáljuk meg, hogy az ötszög csúcspárjai milyen színű utakkal köthetők össze. Ha létezik két olyan csúcspár: $X$, $Y$ és $U$, $V$, amelyek közül $X$ és $Y$ nem köthető össze $1$-es, $U$ és $V$ pár pedig nem köthető össze $2$-es színnel, akkor színezzük ki $PX$-et és $PY$-t $1$-es színnel, $PU$-t és $PV$-t $2$-es színnel, a $P$-ből kiinduló ötödik élt pedig $3$-as színnel (11. ábra).   11. ábra   Ezzel a $G$ gráf egy jó színezését kapjuk. Mivel az $AC$ él $1$-es színű volt, $A$ és $C$ nem köthető össze $1$-es színnel; hasonlóképpen $A$ és $D$ nem köthető össze $2$-es színnel. Ha a $B$, $D$, $E$ csúcsok közül valamelyik kettő nem köthető össze $2$-es színnel, akkor azt a kettőt $U$, $V$-nek, $A$, $C$-t pedig $X$, $Y$-nak választva, az előbbiek szerint $G$-nek egy jó színezését nyerjük. Ha viszont $B$, $D$ és $E$ összeköthető $2$-es színnel, akkor $A$ nem köthető össze $B$-vel és $E$-vel $2$-es színű úton, mert akkor $A$ és $D$ is összeköthető lenne $2$-es színnel. Hasonlóképpen feltehetjük, hogy a $B$, $C$ és $E$ csúcsok összeköthetők $1$-es színnel, míg az $A$ csúcs nem köthető össze a $B$ és $E$ csúcsokkal $1$-es színű úton sem (12. ábra).   12. ábra   Az $A$ csúcs tehát nem köthető össze a $B$, és $E$ csúcsokkal sem $1$-es, sem $2$-es színű úton. Ebből következik, hogy az $AB$ és $AE$ élek színe $3$-as, és az $A$, $B$, $E$ csúcsok között csak ezek az élek alkotnak $3$-as színű utat. Színezzük át $AB$-t $1$-esre, $AE$-t pedig $2$-esre. Ezzel a változtatással nem keletkezhet egyszínű kör. Ezután színezzük ki a $PA$, $PB$ és $PE$ éleket $3$-asra, a $PC$ és $PD$ eleket pedig $1$-esre, illetve $2$-esre (13. ábra).   13. ábra   Ha lenne egyszínű kör, akkor az csak $P$-n keresztül haladhatna, és csak $3$-as színű lehetne, és azt jelentené, hogy az $A$, $B$ és $E$ csúcsok közül valamelyik kettő között még egy $3$-as színű út halad, ami ellentmondás. Ezzel minden $n+1$ csúcsú gráfra igazoltuk az állítást.   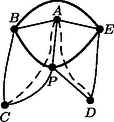Megjegyzések. 1. Az, hogy a teljes ötszög nem síkra rajzolható, például a következőképpen mutatható meg: Kössük össze a pontokat valamilyen sorrendben egymást nem metsző élekkel. A keletkező ötszög belsejében is, rajta kívül is csak két-két pontpárt köthet össze él, ezek a megmaradó csúcspárt elválasztják egymástól (14. ábra).   14. ábra   2. Síkra rajzolható gráfok a síkot lapokra bontják, ezekhez hozzávéve a gráfon kívüli tartomát is. Ha a gráf összefüggő, akkor a lapok $l$, az élek $é$ és a csúcsok $c$ száma között fennáll az Euler-féle $l-é+c=2$ összefüggés. Ha a csúcsok száma legalább $3$, akkor egy lapnak legalább $3$ oldala van, másrészt minden él két lapnak oldala, így $3l\le 2é$. Ezt az Euler-tételbe helyettesítve az $é\le 3c-6$ egyenlőtlenség adódik. Ha minden csúcs legalább $6$-odfokú lenne, akkor ‐ mivel minden él két csúcshoz tartozik ‐, $é\ge c$ teljesülne. 3. Könnyen igazolható, hogy ha egy $k$ csúcsú gráf nem tartalmaz kört, akkor legfeljebb $k-1$ éle van. Ha azt vizsgáljuk, hogy egy tetszőleges $G$ gráf élei mikor színezhetők ki $3$ színnel úgy, hogy ne legyen benne egyszínű kör, akkor szükséges, hogy tetszőleges $k$ pozitív egészre $G$ bármely $k$ csúcsa között legfeljebb $3k-3$ él haladjon. Ez a feltétel gyengébb, mint a síkra rajzolhatóság, és be lehet bizonyítani, hogy nemcsak szükséges, hanem elégséges is.   Surányi János, Kós Géza, Ujváry-Menyhárt Zoltán ${}^{*}$${}^1$