|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A lineáris programozás egy alkalmazott matematikai tudományág, amely a geometriára, az algebrára, a kombinatorikára, a numerikus módszerekre, a függvénytanra és a számítástechnikára támaszkodik. Egzakt matematikai megfogalmazása a következő.
A lineáris programozás feladata
Lineáris egyenlőtlenségekből és lineáris egyenlőségekből álló feltételeknek eleget tevő , , rendezett szám -esek közül ki kell választanunk olyan rendezett szám -est, amelyre egy előírt lineáris (első fokú) függvény a lehető legnagyobb, illetve a lehető legkisebb értéket veszi fel. Előfordulhat, hogy feltételeink ellentmondásosak, továbbá az is, hogy van ugyan a feltételeknek eleget tevő rendezett szám -es, ám nincs véges nagyságú szélsőérték. E két esetben a gyakorlati feladatot rosszul fogalmaztuk meg. Ez a tény az esetek nagy részében nem dönthető el ránézéssel, hanem csak a megoldási módszer alkalmazása során tűnik ki. Ezért a feltételek összeférhetőségének és a véges szélsőérték létezésének az eldöntését is a lineáris programozás feladatához soroljuk.
Néhány lineáris programozásra vezető gyakorlati feladat
Szendvicskészítés. Egy társasági összejövetelre szendvicseket készítünk, mégpedig két fajtát. Ezek egy-egy darabja az alábbi összetételű:
Kenyér van otthon bőven, ám a további összetevők mennyisége már korlátozott. Rendelkezésünkre áll:
Célunk az, hogy a lehető legtöbb szendvicset készítsük. Ha , illetve jelöli az egyes szendvicsfajtákból készítendő mennyiséget, akkor feladatunk a következő: | |
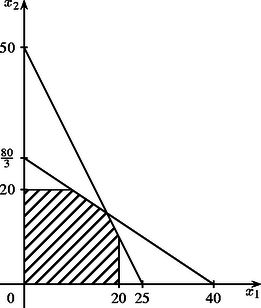
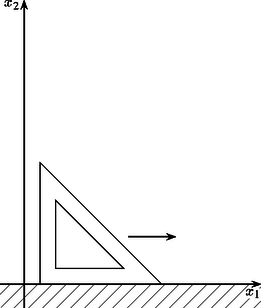
A feladat megoldását grafikusan a következő módon végezhetjük el. Az 1. ábrán a vonalkázott sokszög jelenti a sík azon pontjainak összességét, amelyek eleget tesznek a feladat feltételeinek. Ezek közül a legnagyobb összeget szolgáltató pontot a következő módon választhatjuk ki: egy egyenlőszárú derékszögű háromszög alakú vonalzót végigcsúsztatunk egy másik vonalzón, amely az tengellyel egybeesik ‐ a 2. ábrának megfelelő módon ‐, majd megállunk akkor, amikor a vonalzó átfogójának és a vonalkázott sokszögnek még van közös pontja, de a vonalzó akármilyen kis továbbhaladása esetén ilyen közös pont már nincs. Esetünkben ez az eljárás egyetlen pontot eredményez, amely a egyenesek metszéspontja. Innen adódik, hogy a legnagyobb összeget akkor kapjuk, amikorA programozási nyelvekben elterjedt szokás szerint a számok tizedestört felírásában tizedespontot és nem tizedesvesszőt használunk. és .
Az eredeti gyakorlati feladat megoldását csak közelítőleg kaptuk meg, hiszen nem egész szám, fél szendvicset pedig nem készítünk. Van módszerünk arra is, hogy az , ismeretlenekkel kapcsolatos fenti feltételeken kívül még ezekre az egész értékűség követelményét is előírva, megoldjuk a feladatot. Ezzel a bonyolultabb kérdéssel e helyen nem foglalkozunk. Megjegyezzük, hogy az egész értékűség természetesen nem minden lineáris programozási feladatban jogos követelmény, és még ha jogos is, elhanyagolhatjuk, ha nem tartjuk lényegesnek a meghatározandó darabszámok ily módon adódó csökkenését vagy túllépését.
Ha az eredeti feladattal kapcsolatban az egész értékűséget megkívánjuk, akkor ‐ amint az az előbbi grafikus módszerrel könnyen adódik ‐ három, ugyanazt a maximumot szolgáltató megoldást nyerünk. Ezek a következők: | |
Optimális termelési terv készítése. Egy teherautókat gyártó vállalat egyéves termelési tervet készít. Meg kell határozni, hogy ötféle autótípus mindegyikéből mennyit gyártsanak egy év folyamán. A gyárnak van két nagyobb üzemegysége: a karosszériaüzem és a motorüzem, továbbá öt kisebb szerelőcsarnoka, mindegyik autótípus számára egy-egy. A karosszéria- és a motorüzem egy időben csak egy-egy autótípushoz gyárt karosszériát, illetve motort; be kell osztani tehát, hogy az egy év időt hogyan használják fel az öt autótípus számára. A szerelőcsarnokok egymás munkáit nem tudják átvállalni.
Ha a karosszériaüzem csak egy autótípushoz gyártana karosszériát, akkor 10 000 db legyártásához rendre 1, , 2, és évre volna szükség.
Ha a motorüzem csak egy autótípushoz gyártana motort, akkor 15 000 db legyártásához rendre 1, , 3, 1 és évre volna szüksége.
Az öt szerelőcsarnok kapacitása évente 7500, 5000, 1000, 9000, illetve 3000 autó összeszerelése.
Végül megadjuk, hogy az egyes autótípusok egy-egy darabjának eladása révén a gyár tiszta haszna száz dolláros egységekben kifejezve 35, 45, 50, 30, illetve 40 egység.
Nem törődve azzal, hogy az autók száma csak egész szám lehet, feladatunkat az alábbi módon fogalmazzuk meg: | |
A lineárás programozási feladat megoldása
A lineáris programozási feladat megoldására mind a mai napig a Dantzig által 1951-ben közölt módszert alkalmazzák leginkábbA cikk első, 1979-es megjelenése óta természetesen több más módszert is kidolgoztak, de ezek ismertetésére itt nem térünk ki.. Ennek egy egyszerű variánsát fogjuk ismertetni.
A feladat feltételeinek eleget tevő , , rendezett szám -eseket megengedett megoldásoknak nevezzük. A továbbiakban feltesszük, hogy feladatunk olyan alakú, hogy csupán az , , feltételekben áll egyenlőtlenség, az egyéb feltételekben pedig egyenlőség, közelebbről: lineáris egyenlőség. A szendvicses feladat numerikus megoldása előtt majd példát mutatunk arra, hogy mi módon lehet a feladatot a most említett, ún. kanonikus (egységesített) alakra hozni, ha az eredetileg nem volt ilyen. Még azt is feltesszük, hogy az egyenlőséges feltételek ún. kifejezett alakúak bizonyos ,,változókra'' nézve, amin azt értjük, hogy mindegyik egyenlőséges feltételben van olyan változó, amely a többiekben nem szerepel (másképpen kifejezve: a többiekben zéró együtthatóval szerepel). Ilyen pl. az alábbi feltételrendszer: | | (1) |
amely kifejezett az , , változókra nézve. A kifejezett változókat más néven bázisváltozóknak is nevezzük. Még azt is feltesszük, hogy ha a bázisváltozóktól különböző többi változó helyébe zérót helyettesítünk, akkor az egyenlőségekből a bázisváltozók számára automatikusan adódó értékek nemnegatívak. A fenti példában pontosan ez a helyzet, ugyanis és helyébe zérót téve, az , , adódik.
Ha a kanonikus alakú feladat eredetileg nem ilyen, akkor is ilyen alakúra hozható, feltéve, hogy egyáltalán van megengedett megoldáa, amint azt a későbbiekben megmutatjuk.
Most egy olyan feladattal foglalkozunk, amelyben maximumot keresünk. A minimum-feladat erre visszavezethető, ha a minimalizálandó kifejezést -gyel megszorozzuk. A maximalizálandó kifejezést célfüggvénynek, a legnagyobb célfüggvényértéket adó megengedett megoldást ‐ ha ilyen egyáltalán van ‐ optimális megoldásnak nevezzük. Általában, ha egy halmaz minden eleméhez egyértelműen hozzárendelünk egy számot, akkor ezt a hozzárendelést függvénynek nevezzük. Most a feltételek által meghatározott , , rendezett szám -esek mindegyikéhez rendelünk hozzá egy-egy számot, ily módon alkotjuk meg a célfüggvényt. Például az (1) és az alábbi | | (2) |
nemnegativitási feltételeknek eleget tevő , , , , rendezett számötösökön értelmezhetjük az alábbi célfüggvényt: | | (3) |
Az (1) egyenlőségekből az , , változók számára adódó kifejezéseket (3) jobb oldalán a megfelelő helyekre behelyettesítve a célfüggvényre olyan alak adódik, amelyben , , már nem (vagy ha úgy tetszik, zéró együtthatóval) szerepel, mégpedig: Azt a feladatot, amelyben a (4) célfüggvény maximalizálandó az (1) és a (2) feltételek mellett, az alábbi alakban írjuk fel: | |
A feladatot a konstansok és az együtthatók alábbi táblázatából egyértelműen rekonstruálhatjuk:
1. tábla
A táblában a zérók kiírása vagy elhagyása tetszés szerint történhet. A tábla bal oldalon a kifejezett változókat és a célfüggvény függő változóját írjuk fel, a tábla tetején pedig felsoroljuk valamennyi változót. Most két tételt említünk meg, amelyeket a lineáris programozási feladat megoldásakor használunk fel.
1. tétel. Ha a tábla felső sorában álló számok ‐ az elsőt nem számítva ‐ mind nemnegatívak, akkor a kifejezett változókat a mellettük álló konstansokkal, a többi változót 0-val egyenlővé téve, a feladat optimális megoldását nyerjük.
A tétel igaz voltát az (5) feladat egy módosítottján szemléltetjük. A módosítás abban áll, hogy az együtthatóját a célfüggvényben megváltoztatjuk, helyett 7-et írunk a zárójelen belül, miáltal az új célfüggvény a következő lesz: Minthogy , , azonnal adódik, hogy ; és a célfüggvényértéket valóban megkapjuk, ha , továbbá , , .
2. tétel. Ha a tábla felső sorában ‐ az első számot nem számítva ‐ van olyan negatív szám, hogy az alatta álló számok mind nempozitívak, akkor a célfüggvény nem korlátos felülről, azaz akármilyen nagy számnál nagyobb értéket felvesz alkalmas megengedett megoldás esetén.
Ezt a tételt is az (5) feladat egy módosítottján szemléltetjük. A módosítás most abban áll, hogy az első és a második egyenlőséges feltételben a zárójelen belül együtthatóját helyett -ra, illetve 4 helyett -re változtatjuk. Az így nyert feladatban választunk egy tetszőleges , , , , megengedett megoldást; -et növelve, az egyenlőségek érvényben tarthatók az , , bázisváltozók értékeinek alkalmas megválasztásával, miközben a nem bázisváltozók értékét nem változtatjuk (most az tartozik ebbe a kategóriába). Eközben a célfüggvény értéke minden határon túl nő, vagyis tényleg nem korlátos felülről.
A fenti két tételben két különböző típusú tábláról van szó. Van egy harmadik típus is, amelyben a felső sorban ‐ az első számot kihagyva ‐ van negatív szám, és az alatta álló számok között van legalább egy pozitív. Mindegyik tábla a három kategória valamelyikébe tartozik. Az (5) feladathoz tartozó 1. tábla a harmadik csoportba tartozik.
Ekkor eljárásunk a következő: a bázisváltozók valamelyikét megszüntetjük mint bázisváltozót, helyette egy olyan változó, mely eddig nem volt bázisváltozó, azzá válik. Az új bázisváltozó céljára minden olyan változó megfelel, amelynek a célfüggvényben a kerek zárójelen belüli együtthatója negatív. Ezek közül tetszőlegesen kiválasztunk egyet bejövő változó gyanánt; ám a kimenő változó meghatározása már nem tetszőleges. Ezt úgy kell megválasztanunk, hogy a célfüggvényben szereplő konstans lehetőleg növekedjék, de legalábbis ne csökkenjen, a feltételek konstansai pedig maradjanak nemnegatívak az új bázisváltozk esetében. Mindkét célt elérjük, ha vesszük azokat az egyenlőséges feltételeket, amelyekben a bejövő változó ‐ zárójelen belüli ‐ együtthatója pozitív, majd meghatározzuk mindegyik ilyen egyenlőségen belül a konstans tag és a bejövő változó együtthatójának a hányadosát és amelyik egyenlőség esetében ez a hányados a legkisebb, annak a bázisváltozója lesz a kimenő változó. Ezek után az előbbi módon kiválasztott egyenlőséges feltételt a bejövő változó együtthatójával végigosztjuk, majd a célfüggvényből és a többi egyenlőséges feltételből ugyanezt a változót kiküszöböljük az új bázisváltozóhoz tartozó egyenlőséges feltétel alkalmas konstansszorosainak hozzáadásával. Megjegyzendő, hogy az új feltételek a régiekkel egyenértékűek, a célfüggvény pedig semmit nem változik értékében, csak alakjában, hiszen csupán zérót adtunk hozzá.
Bár a fentiek alapján nagyjából világos, hogy hogyan nyerjük az új táblát a régiből, a teljesség kedvéért ezt a szabályt röviden összefoglaljuk. Ha az változó bejön a bázisba, pedig kimegy a bázisból, akkor:
az új táblában sorát úgy nyerjük, hogy a régi táblában az -nek megfelelő sort végigosztjuk azzal az elemével, amelyik az oszlopában áll;
az új tábla minden egyéb sorát úgy származtatjuk, hogy a neki megfelelő, régi táblabeli sor oszlopában álló elemével az új tábla -nak megfelelő sorát elemenként végigszorozzuk, majd az így kapott sort elemenként levonjuk a régi táblabeli sorból.
Alkalmazzuk a fent leírt lépést az (5) feladatra. Csak egy negatív szám van a tábla felső sorában az utolsó öt pozícióban, ez -hez tartozik, tehát bejön. Minthogy és a minimumot az első egyenlőséges feltételben kapjuk, ezért a kimenő bázisváltozó. Az új feladatot szükségtelen kiírni, elég az új tábla megadására szorítkozni, ez pedig a következő:
2. tábla
Minthogy a felső sor utolsó öt pozíciójában minden szám nemnegatív, optimális megoldáshoz jutottunk, amely a következő: | |
Ezt a módszert nevezik Dantzig módszerének.
Ha Dantzig módszerének végrehajtása során a tábla bal felső sarkában álló szám állandóan növekszik, akkor soha nem térhet vissza a bázisváltozók egy olyan összessége, amely korábban már szerepelt. A kifejezett változók ugyanis a teljes táblát és így a bal felső sarokban álló elemet is egyértelműen meghatározzák. Minthogy pedig csak véges sok különböző módon lehet a kifejezett változókat kiválasztani, az eljárásnak véges sok lépés után be kell fejeződnie, vagy az 1. vagy a 2. tételnek megfelelő tábla elérésével. Ha a 2. tételnek megfelelő táblához jutunk, akkor nyilván rosszul fogalmaztuk meg az eredeti gyakorlati feladatot, ahhoz kell tehát visszatérnünk.
Most a szendvicskészítés példájának megoldását mutatjuk be. Az eredeti feladat négy egyenlőtlenséges feltételéhez segédváltozókat vezetünk be úgy, hogy a négy feltétel mindegyikében egyenlőség álljon fenn. Az új feladat a következő: | |
E feladatnak nyilván akkor és csak akkor van megengedett megoldása és véges optimuma, ha az eredeti feladatnak, és az optimumértékek (a célfüggvények értékei az optimális megoldásokon) egyenlők. Segédváltozóinknak ,,fizikai'' jelentést is tulajdoníthatunk. Ezek megadják a megmaradó vaj, sonka, franciasaláta és sajt mennyiségét. Segédváltozóink még abban is segítenek bennünket, hogy máris van egy kifejezett változó rendszerünk.
A (6) feladatot előbb az (5) feladatnak megfelelő alakra hozzuk: | |
Az ehhez tartozó tábla, majd a megoldási módszer alkalmazása révén adódó további táblák a következők:
1. tábla
2. tábla
3. tábla
4. tábla
Az optimális megoldás a következő: , , , , , . Eszerint a vajat és a sonkát teljesen felhasználjuk, franciasalátából marad dkg, sajtból pedig 10 dkg.
Vegyük észre, hogy az egymást követő táblák tetején mindig az összes változó szerepel ugyanabban a sorrendben, míg az bal oldalon a bejövő változó mindig a kimenő változó helyére kerül, a többi változó azonban helyben marad.
Az előző szakaszban tárgyalt megoldási módszer esetében nincs garanciánk arra, hogy véges sok lépéssel eljutunk az 1. vagy a 2. tételnek megfelelő állapothoz. Ismeretesek olyan példák, amelyekben néhány lépés után visszajutunk ugyanazokhoz a bázisváltozókhoz, amelyekből kiindultunk. Azt mondjuk, hogy ekkor az eljárás ciklizál. A későbbiekben ismertetni fogjuk Beale [1] példáját, amely megmutatja, hogy a ciklizálás lehetséges, előbb azonban a ciklizálás elkerülésére vonatkozó módszert tárgyaljuk. A módszer lényegében Charnes-tól származik, ám annak egy elegánsabb változata.
A ciklizálásra akkor kerülhet sor, amikor a kimenő változó meghatározása nem egyértelmű, mert a megalkotott hányadosok minimuma több sor esetében is fellép. Ilyen esetben a következő táblában a bal oldalon álló oszlopban legalább egy zérus keletkezik. Az ezt követő táblában a bal felső sarokban álló elem biztosan változatlan marad, és ha ez sorozatosan előfordul, fennáll a ciklizálás veszélye.
Mielőtt a módszert ismertetnénk, bevezetjük a lexikografikusan pozitív (-pozitív) rendezett szám -es fogalmát. Minthogy értéke a tárgyalás során mindig ismert lesz, és a rendezett szám -eseink egymás mellé egy sorban elhelyezett számokból állnak majd, elég lesz egyszerűen csak -pozitív sorokról beszélni. Egy sort akkor nevezünk -pozitívnak, ha az elemek között van zérustól különböző, és balról jobbra haladva az első nem zérus elem pozitív. Ilyen pl. az alábbi, öt elemből alkotott sor: viszont nem ilyen az alábbi: Ha két egyenlő számú elemből alkotott sor esetében az elsőből a másodikat elemenként levonva -pozitív sort kapunk, akkor azt mondjuk, hogy az első lexikografikusan nagyobb, mint a második. Például a sor lexikografikusan nagyobb, mint az alábbi ugyanis az elemenként vett különbség a -pozitív sort eredményezi.
Egy kifejezett alakú lineáris programozási feladathoz tartozó táblát lexikografikusan pozitívnak (-pozitívnak) nevezünk, ha annak második és ez alatti összes többi sora -pozitív. Ebben a cikkben az eddig felírt valamennyi tábla -pozitív.
A ciklizálás elkerülésére vonatkozó ún. lexikografikus szabály (-szabály) a bejövő változó ismeretében mindig egyértelműen dönt a bal szélső kimenő változó felől. A bejövő változóra vonatkozó szabály változatlan, tetszés szerint választhatunk egy negatív elemet a felső sorban, a bal szélső elemtől eltekintve. A kiválasztott elemnek megfelelő változó bejön. Ezután a táblában a most kiválasztott elem alatti pozitív (zérus nem lehet!) elemekkel rendre elosztjuk azokat a sorokat, amelyekben ezek a pozitív elemek állnak (vigyázzunk, a teljes sorokat kell osztani, a bal szélső elemek most nem hagyhatók el!), majd vesszük az így kapott sorok közül azt, amelyik a lexikografikusan legkisebb. Az ennek a sornak megfelelő változó fog kimenni, ezt nevezzük -szabálynak.
Az -szabállyal kapcsolatban megemlítjük, hogy véges sok különböző, de ugyanannyi elemből álló sor között mindig van egy és csakis egy lexikografikusan legkisebb, ami azt jelenti, hogy ezt a továbbiak akármelyikéből elemenként levonva, mindig -pozitív sort kapunk. Ennek az állításnak a belátását az olvasóra bízzuk. A mi vizsgálatainkban csakis olyan tábla fordul elő, amelynek a második és ez alatti sorai páronként nem arányosak, ugyanis ha kifejezett változó, akkor abban a sorban, amely mellett van, található egy 1-es olyan helyen, hogy annak oszlopában minden egyéb elem zérussal egyenlő.
Az -szabály alkalmazásakor megkívánjuk, hogy -pozitív táblából induljunk ki. Ez könnyen elérhető, ha változóinkat átszámozzuk oly módon, hogy a bázisváltozók az elsők legyenek, tehát számú bázisváltozó esetén éppen , , legyenek azok. Ez esetben ugyanis a bal oldalon a bázisváltozók melletti számok közül ha egyesek zérussal egyenlők is, soraikban az első nem zérus elem -gyel lesz egyenlő, tehát a tábla -pozitív lesz.
Könnyen belátható, hogy ha -pozitív táblából indulunk ki, és a kimenő változó meghatározására mindig az -szabályt alkalmazzuk, akkor minden további tábla -pozitív lesz, a legfelső sor pedig állandóan lexikografikusan növekszik. Ezt nemsokára Beale példáján szemléltetjük, ahonnan az állítás általános érvénye világosan látszik majd. Most csupán leszögezzük, hogy a legfelső sor állandó -növekedése miatt egyetlen bázisváltozó-rendszer sem térhet vissza (mert akkor a legfelső sor is visszatérne, ám egy sor nem lehet egyenlő egy nála lexikografikusan nagyobb sorral), ahonnan következik, hogy véges sok lépés után az eljárás véget ér vagy az 1., vagy a 2. tételnek megfelelő állapot elérésével. Ezt az eredményt tételszerűen is megfogalmazzuk az alábbi módon:
3. tétel. A lexikografikus módszer véges sok lépéssel véget ér.
Most pedig bemutatjuk Beale példáját. Előbb a lexikografikus módszert alkalmazzuk, hogy lássunk erre vonatkozó példát. Azután pedig megmutatjuk, hogy az eljárás ciklizálhat, amennyiben csupán az előző szakaszban ismertetett módszert alkalmazzuk. A lineáris programozási feladat (az általunk megkívánt alakban) a következő: | |
Az ehhez a feladathoz tartozó tábla a következő:
1. tábla
A felső sorban -et kiválasztva, alatta két helyen találunk pozitív számot, ezek: és . Azt a sort, amelyikben áll, végigosztjuk -del, azt a sort pedig, amelyikben áll, végigosztjuk -del. Ilyenformán az alábbi sorokat kapjuk: | | (8) |
Minthogy a két sor közül az alsó lexikografikusan kisebb, ezért megy ki. Helyébe jön be.
Lássuk most egy kicsit részletesebben, hogy miért növekszik a felső sor lexikografikusan, és miért lesz -pozitív az új tábla. Az új felső sort úgy kapjuk meg, hogy a mostani felső sorból levonjuk sorának a számmal elemenként vett szorzatát, azaz hozzáadjuk a felső sorhoz sorának -szeresét. Minthogy sora -pozitív, ebből azonnal adódik, hogy a felső sort ezáltal lexikografikusan megnöveltük.
A lexikografikus növekedés abból adódik, hogy a negatív áll a felső sorban a sarokelem felett. Ha a sarokelem oszlopában máshol negatív szám állna, akkor az új táblában ugyanezen megfontolás alapján a megfelelő sor lexikografikusan megnőne, tehát az új táblában ez a sor -pozitív maradna. Ez az eset most nem fordul elő, csak a teljesség kedvéért említjük.
Ha a sarokelem oszlopában valamelyik szám 0, akkor az a sor, amelyikben ez a 0 áll, nem változik. Eszerint ez a sor is -pozitív marad. Esetünkben ilyen az változó sora.
Az új táblában sora oly módon kapható meg a régi táblabeli -höz tartozó sorból, hogy ezt -del végigosztjuk. Az új sor tehát -pozitív.
Végül ami sorát illeti az új táblában, ez éppen az -szabály alkalmazása miatt lesz -pozitív. Ugyanis új sora egyenlő az alábbival: | |
ez pedig -pozitív, minthogy (8)-ban a felső és az alsó sor különbsége -pozitív. (Amikor valamely sor zárójele elé egy számot írunk, ez azt jelenti, hogy a sor minden eleme ezzel a számmal végigszorzandó.) Ezek után a második tábla a következő:
2. tábla
Vegyük észre, hogy a felső sor lexikografikusan nagyobb, mint az 1. tábla felső sora. A 2. táblában az -szabály nem jut szerephez, mert egyedül jöhet be, és egyedül mehet ki. A harmadik és egyben az optimális megoldást szolgáltató tábla így alakul:
3. tábla
Az optimális megoldás tehát a következő: , , , , , , .
A ciklizálás lehetőségét az alábbi táblák sorozata mutatja:
1. tábla
2. tábla
3. tábla
4. tábla
5. tábla
6. tábla
7. tábla
Induló bázisváltozók keresése
A szendvicskészítés példájában könnyű volt induló bázisváltozókat találni. A bevezetett segédváltozók megfeleltek e célra. Nem mindig van ilyen könnyű dolgunk. Ha a (6) feladatban a jobb oldalon akár csak egy szám is negatív volna, máris bajban volnánk, hiszen kikötöttük, hogy a nem bázisváltozókat zérussal egyenlővé téve, a bázisváltozók számára adódó értékek nemnegatívak legyenek.
Az induló bázisváltozók keresésének általános módszere az ún. kétfázisú módszer. Olyan feladatból indulunk ki, amelyben a változók nemnegativitási feltételein kívül minden további feltétel egyenlőséges. Ilyen pl. az alábbi feladat: | |
A kétfázisú módszer első fázisában önkényesen bevezetünk minden egyenlőséges feltételhez a bal oldalon egy további változót, ezeket mesterséges változóknak nevezzük. Ezután előírjuk, hogy ezek is nemnegatívak legyenek, és megfogalmazzuk azt a feladatot, amely a mesterséges változók összegének minimalizálásában áll, vagy ami ugyanaz, maximalizálandó a mesterséges változók összegének -szerese. A fenti feladat esetében ily módon a következőkre jutunk: | |
ahol és a mesterséges változók. E feladat megoldása:
1. tábla
2. tábla
3. tábla
Optimális megoldáshoz és egyben új bázisváltozókhoz érkeztünk. A 3. tábla alapján a feladat egyenlőséges feltételeinek új, a korábbiakkal egyenértékű alakja a következő: | |
Ha itt és helyébe zérót helyettesítünk, akkor a (9) feladat egyenlőséges feltételével egyenértékű feltételeket kapunk, amelyek kifejezettek az , változókra nézve. Ezzel az első fázis véget ér, következik a második fázis. Ez abban áll, hogy a (11) feltételekből ily módon nyert feltételekhez hozzávesszük a nemnegativitási feltételeket, továbbá az eredeti célfüggvényt és megoldjuk a feladatot. A második fázis feladatának alakja tehát: | |
A második fázis egy lépésben befejeződik, az optimális megoldás: | |
Az eredeti változókat a mesterséges változókkal szemben ,,fizikai változóknak'' is szokás nevezni.
A kétfázisú módszerrel kapcsolatban még a következőket fontos tudni.
Ha az első fázis befejeződik és az optimumérték 0-tól különbözőnek adódik, akkor ez azt jelenti, hogy az eredeti feladatnak nincs megengedett megoldása.
Ha az első fázis végén az optimumérték 0-val egyenlő, de marad mesterséges változó a bázisváltozók között, akkor az utolsó táblában a bal oldali oszlopban a mesterséges változók melletti számok szükségszerűen 0-val egyenlők. Ilyenkor először is a bázison kívüli mesterséges változókat a feladatból egyszerűen elhagyjuk. A bázisban bennmaradt mesterséges változókat pedig megpróbáljuk egymás után fizikai változókra kicserélni. A csere után ezeket a mesterséges változókat is egyszerűen elhagyjuk majd. Ha pl. az első fázis végén a bázison kívüli , , mesterséges változók elhagyása után az alábbi feltételekre jutottunk: | |
ahol a bázisban bennmaradt mesterséges változó, akkor a legalsó sor segítségével elimináljuk pl. -et a felső három sorból. Ezáltal kimegy a bázisból, pedig bejön. Ilyen csere csak akkor nem volna lehetséges, ha az utolsó sorban és együtthatói zéróval lennének egyenlők. Képzeljük el, hogy ez következett be. Ekkor azt a konzekvenciát vonjuk le, hogy az eredeti, mesterséges változókkal még el nem látott feladatban az utolsó feltétel az első három feltétel alkalmas konstansszorosainak összegeként áll elő, vagyis az utolsó feltétel felesleges. Általában, ha az mesterséges változó nem távolítható el a bázisból egy fizikai változó behozatalával, akkor az eredeti feladatban felesleges az a feltétel, amelyhez az -et vezettük be. Az első fázis végén tehát a felesleges egyenlőségeket is felfedezzük.
|
PDF | MathML 
