Kezdőlap


Cím:	Beszámoló az 1999. évi Eötvös-versenyről
Szerző(k):	Gnädig Péter , Radnai Gyula
Füzet:	2000/április, 240 - 246. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1999. október 15-én rendezte meg az Eötvös Loránd Fizikai Társulat hagyományos őszi tanulóversenyét, az Eötvös-versenyt, melyen 156 hazai, 3 szlovákiai és 1 romániai versenyző indult. Az első feladatot 15 versenyző tudta hibátlanul megoldani, a másodikat 40, a harmadikra azonban csupán egy tökéletes megoldás érkezett. Részben jó megoldás elég sok volt.
Ismertetjük a feladatokat, azok helyes megoldását, végül a verseny végeredményét.

1. Egy szuperszonikus vadászgép 900 m magasan repül el felettünk, vízszintes irányban. 1 km messze van tőlünk, amikor először meghalljuk a hangját. Milyen irányból halljuk a repülőgép hangját akkor, amikor már 2 km messze van tőlünk a gép?

(Radnai Gyula)

Megoldás. Az 1. ábrán az

M

megfigyelő fölött elhaladó repülőgépből egyenlő időközönként kibocsátott hanghullámokat ábrázoltuk.
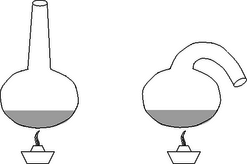
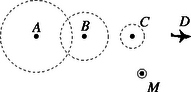
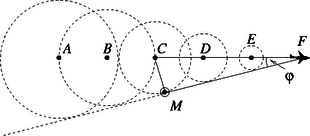
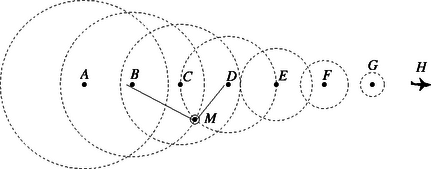
A szuperszonikus repülőgép sebessége nagyobb, mint a hang sebessége a levegőben. Jól látszik, hogy a repülőgép már elhaladt a megfigyelő felett, de a hangja még nem ért el a megfigyelőhöz. Az 1. ábrán a repülőgép éppen a

D

pontban van, ez előtt

τ

idővel volt a

C

pontban,

2 τ

idővel előtte a

B

pontban,

3 τ

idővel előtte az

A

pontban.

A B = B C = C D = v τ

(

v

a repülőgép sebessége). Természetesen a közbülső pontokban is bocsát ki hangot a repülőgép, az áttekinthetőség kedvéért ezeket nem tüntettük fel.
Akármekkora

τ

időközt választhatunk az ábrázolásra, most azonban éppen akkorát választottunk, hogy az 1. ábrán ábrázolt helyzethez képest pontosan

2 τ

idő múlva érjen el az

M

megfigyelőhöz a repülőgép hangja; ezt mutatja a 2. ábra. Itt a repülőgép már az

F

pontban van, s a

C

pontból indult hanghullám éppen

M

-be ért. (A többi pontból jövő hang még nem érte el

M

-et.)
Mivel

\vec{C M} ⊥ \vec{F M}

, a

C M F

háromszög derékszögű. Ameddig a gép megtette a

C F

utat, addig a hang a

C M

távolságot futotta be. (Ábránkon ez az idő

3 τ

.) Az összes pontból jövő hanghullán eredője az a kúp alakú ,,fejhullám-felület'', amelynek egyik alkotója a 2. ábrán az

F M

egyenes. E kúp fél nyílásszöge az ún. Mach-szög, amelyre

\begin{matrix} sin φ = \frac{c}{v} \end{matrix}

(

c

a hangsebesség,

v \geq c

). Ennek az általánosan érvényes összefüggésnek a felhasználásával fogjuk megoldani a feladatot.
Tekintsük a 3. ábrát, melyen a balról jobbra haladó repülőgép az

F

pontban van, amikor először jut el a hangja az

M

pontba. Az ábrából leolvasható, hogy a Mach-szögre (a megadott adatok felhasználásával)

\begin{matrix} \begin{matrix} sin φ = \frac{0, 9 km}{1 km} = 0,9, \\ ahonnan φ = 64, 16^{\circ} . \end{matrix} \end{matrix}

Abban a pillanatban, amikor a repülőgép az

M

megfigyelőtől 2 km távol lévő

R

pontban van, a megfigyelő azt a hangot hallja, amit a gép egy korábbi időpontban adott ki. Ahol ekkor volt a repülőgép, azt a pontot jelöljük

P

-vel. Feladatunk tehát az

M P

irány meghatározása. Kérdezhetjük például azt, hogy ez az irány mekkora szöggel marad le az

M R

iránytól, vagyis hány fokkal hátrábbról halljuk a hangot, mint ahol látjuk a gépet. Ezt a szöget (melyet a 3. ábrán

μ

-vel jelöltünk) az

M P R ▵

-ből a szinusztétel segítségével határozhatjuk meg:

\begin{matrix} \frac{sin ϱ}{sin μ} = \frac{P M}{P R} . \end{matrix}

Mivel

sin ϱ = \frac{0, 9 km}{2 km} = 0, 45

(ahonnan

ϱ = 26, 74^{\circ}),

valamint

\begin{matrix} \frac{P M}{P R} = \frac{c t}{v t} = \frac{c}{v} = sin φ = 0,9, \end{matrix}

ezért

\begin{matrix} sin μ = \frac{0, 45}{0, 9} = \frac{1}{2}, azaz μ_{1} = 30^{\circ}, illetve μ_{2} = 150^{\circ} . \end{matrix}

Meglepőnek tűnhet, hogy a

μ

szögre két érték is adódott, pedig csak egy hegyesszögre számítottunk. Vajon a tompaszög is megoldása az eredeti fizikai problémának? Bizony az! Már a 2. ábrából is látszik, hogy ha a repülőgép túlhaladt az

F

ponton, akkor nemcsak a

C

pont utáni helyekről (pl.

D

-ből és

E

-ből) induló hullámok érik el fokozatosan az

M

pontot, hanem egyidejűleg azok a hullámok is odaérnek, amelyeket még a

C

pontba érkezése előtt bocsátott ki a gép (pl.

B

-ből,

A

-ból). Egy ilyen helyzetet mutat a 4. ábra, ahol éppen a

B

és a

D

pontok közeléből indult hullámok érik el egyszerre

M

-et. (A

C

-ből indult hullám már túlhaladt

M

-en). Az első ,,hangrobbanás'' után tehát mindig két irányból halljuk a repülőgép hangját, igaz, általában az ,,elölről'' jövőt halljuk erősebben.
Megjegyzés. A megoldók a hallott hang

M P

irányának meghatározásakor általában a vízszintes vagy függőleges iránnyal bezárt szögeket adták meg. A helyes eredmények a vízszintessel bezárt szögekre:

μ_{1} + ϱ = 56, 74^{\circ}

, illetve

180^{\circ} - (μ_{2} + ϱ) = 3, 26^{\circ}

; a függőlegessel bezárt szögek pedig:

90^{\circ} - (μ_{1} + ϱ) = 33, 26^{\circ}

és

μ_{2} + ϱ - 90^{\circ} = 86, 74^{\circ}

2. Két egyébként egyforma lombik közül az egyiknek a nyaka egyenes, a másiké lefele görbül, az 5. ábra szerint. A két lombikba azonos mennyiségű

A)

vizet,

B)

étert

töltünk, és gondoskodunk róla, hogy mindkét lombikban a folyadék hőmérséklete
az

A)

esetben

100^{\circ}

C,
a

B)

esetben

34, 6^{\circ}

C

legyen. Melyik lombikból fogy el hamarabb a folyadék az egyik, illetve a másik esetben?

(Károlyházy Frigyes)

Megoldás. A megadott

100^{\circ} C

a víz,

34, 6^{\circ} C

pedig az éter normál nyomás melletti forráspontja. A víz móltömege 18 g/mol, az éter

[{(C_{2} H_{5})}_{2} O]

móltömege 74 g/mol. Igaz, a forráspont környékén egyetlen reális gáz sem viselkedik ideális gázként, az mégis joggal feltételezhető, hogy a vízgőz sűrűsége kisebb, az étergőz sűrűsége pedig nagyobb marad a levegő sűrűségénél. (A vízgőz ,,könnyebb'', az étergőz ,,nehezebb'' a levegőnél.)
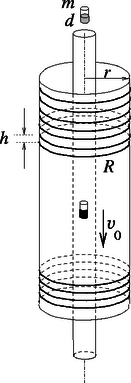
Tekintsük először az

A)

esetet, amikor mindkét lombikba vizet töltöttünk. Ekkor az egyenes nyakú lombikban képződő vízgőz előbb-utóbb betölti a lombik nyakát, azonban nem maradhat stabilan a nála ,,nehezebb'' levegő alatt, hanem felszáll, helyet adva a levegőnek, valamint az újabb és újabb vízgőzképződésnek; így a víz hamarosan elforr.
A görbe nyakú lombik nyakát is betölti a vízgőz, innen azonban csak ,,lefelé'' tudna kiszabadulni, miközben a sűrűbb levegőnek kellene felfelé, a vízgőz helyére áramlania. Ez nem történik meg olyan hevességgel, mint az egyenes nyakú lombiknál, mert most csak diffúzióval tud eltávozni a vízgőz, ami viszont lassú folyamat. Az

A)

esetben tehát a vízgőz az egyenes nyakú csőből szabadul ki gyorsabban, vagyis ebből a lombikból forr el hamarabb a víz.
Nyilvánvaló, hogy a

B)

esetben, amikor a forráspontján tartott éter van a lombikokban, a helyzet éppen fordított. Az egyenes nyakú lombik nyakában megül az étergőz, nem fog felszállni a nála kisebb sűrűségű levegőbe. A nyak felső végénél diffundálnak az étermolekulák a levegőbe, ezért csak hosszú idő alatt forr el és távozik az éter a lombikból.
A lefelé görbülő nyakú lombik nyakából viszont ,,kifolyik'' a nehéz étergőz a levegőbe, helyére nemcsak levegő, hanem a lombikból újabb étergőz áramlik, gyorsítva ezzel az éter elforrását.

3. Hosszú, keskeny, függőleges üvegcsövet egy vele azonos tengelyű, de sokkal szélesebb,

r

külső sugarú másik üvegcső vesz körül. E szélesebb csövön sűrűn, egymástól

h

távolságra elhelyezkedő,

R

ellenállású körvezetők vannak.
Ha a keskeny csőbe egy

m

tömegű,

d

erősségű (mágneses dipólnyomatékú) kicsiny rúdmágnest ejtünk, az viszonylag hamar elér egy állandó

v_{0}

sebességet, amellyel egyenletesen süllyed.(6. ábra.)
További kísérleteink során a fenti öt mennyiség (

m

d

h

R

r

) közül az egyiket mindig a kétszeresére növeljük, miközben a másik négyet nem változtatjuk meg. Hányszorosára nő az egyes esetekben a kicsiny rúdmágnes állandósult végsebessége?
Az eredeti eset:

m, d, h, R, r

; ekkor

v = v_{0}

a)

(

2 m

d

h

R

r

);

v_{a} / v_{0} = ?

b)

(

m

2 d

h

R

r

);

v_{b} / v_{0} = ?

c)

(

m

d

2 h

R

r

);

v_{c} / v_{0} = ?

d)

(

m

d

h

2 R

r

);

v_{d} / v_{0} = ?

e)

(

m

d

h

R

2 r

);

v_{e} / v_{0} = ?

A mechanikai súrlódástól és a közegellenállástól, továbbá a körvezetők önindukciójától és kölcsönös indukciójától eltekinthetünk.

(Gnädig Péter)

Megoldás¹. Számítsuk ki, mennyi energia disszipálódik (mennyi

Q

hő fejlődik) egyetlen körvezetőben, miközben a mágnes keresztülesik rajta. Kétféleképpen is következtethetünk erre a

Q

mennyiségre: egyrészt az energiaviszonyok összevetéséből, másrészt dimenzionális megfontolásokból.
Ha az

m

tömegű mágnes egyenletesen mozog függőlegesen lefelé a csőben és

L

utat tesz meg, helyzeti energiája

m g L

értékkel csökken. Eközben áthalad

L / h

darab körvezetőn, mindegyikben

Q

hőt fejleszt, és mivel a mágnes mozgási energiája nem változik, fenn kell álljon, hogy

\begin{matrix} m g L = Q L / h, azaz Q = m g h . \end{matrix}

Milyen fizikai mennyiségektől és milyen módon függhet

Q

? Nyilván függ a hőfejlődés a kicsiny mágnes jellemzőitől (a

d

dipólnyomatéktól és a

v

sebességtől), továbbá a körvezető adataitól (az

r

sugártól és a vezető

R

elektromos ellenállásától):

\begin{matrix} Q = F (d, v, r, R), \end{matrix}

ahol

F

valamilyen négyváltozós függvény, melynek pontos (vagy legalább arányossági tényezők erejéig határozott) alakja megadná a feladat valamennyi kérdésére a választ.
Ha dimenzionális megfontolásokkal akarjuk ,,kitalálni'', hogyan függ

F (d, v, r, R)

az egyes változóitól, nem szabad megfeledkeznünk arról, hogy

Q

a felsorolt mennyiségek mellett függhet még

μ_{0}

-tól (a vákuum permeabilitásától), ami ugyan nem változó, hanem egy meghatározott mértékegységű és nagyságú mennyiség, de a hőfejlődés képletében (lévén az mágnességgel kapcsolatos folyamatok eredménye) ez a fizikai állandó is felbukkanhat. A keresett összefüggés tehát

\begin{matrix} Q = G (d, v, r, R, μ_{0}), \end{matrix}

alakú, ahol

G

egy ötváltozós függvény, melyet azonban az SI itt előforduló négy alapmértékegységének (kg, m, s, A) vizsgálatából nem lehet meghatározni.
A feladat mégis megoldható a dimenzióanalízis módszerével, ugyanis a hőfejlődés és az

R

ellenállás közötti összefüggés (a többi adat rögzített értéke mellett) fordított arányosság kell legyen (azaz

Q \propto 1 / R

), hiszen az áram hőhatása (adott módon változó indukált feszültség mellett) az ellenállás reciprokával arányos. Mondhatjuk tehát, hogy

\begin{matrix} Q \propto \frac{1}{R} f (d, v, r, μ_{0}), \end{matrix}

ahol

f (d, v, r, μ_{0})

már csak 4 fizikai mennyiségtől függ.
Írjuk fel az egyes fizikai mennyiségek mértékegységét:

\begin{matrix} [Q] = \frac{kgm^{2}}{s^{2}}, [1 / R] = \frac{s^{3}A^{2}}{k g m^{2}} [v] = \frac{m}{s}, [d] = Am^{2}, [r] = m, [μ_{0}] = \frac{kg m}{A^{2} s^{2}} . \end{matrix}

Ha a keresett

f

függvényt hatványfüggvény alakban próbáljuk felírni²:

\begin{matrix} h (d, v, r, μ_{0}) \propto d^{α} \cdot v^{β} \cdot r^{γ} \cdot μ_{0}^{δ}, \end{matrix}

akkor a 4 független mértékegység hatványainak összehasonlításából a kitevőkre

\begin{matrix} α = 2, β = 1, γ = - 3, δ = 2 \end{matrix}

adódik. Ezek szerint

\begin{matrix} Q = m g h \propto \frac{{(μ_{0} d)}^{2} v}{R r^{3}}, \end{matrix}

vagyis a mágnes esési sebességének és a többi paraméternek a kapcsolata:

\begin{matrix} v \propto \frac{m h R r^{3}}{d^{2}} . \end{matrix}

Ez a formula a feladat valamennyi kérdésére megadja választ: akár a tömeget, akár a menettávolságot, vagy a körvezetők elektromos ellenállását növeljük az eredeti érték kétszeresére, a mágnes esési sebessége 2-szer nagyobb lesz. Kétszer erősebb mágnes az eredetinél 4-szer lassabban fog mozogni, végül pedig a körvezetők sugarának kétszerezése a sebességet az eredeti érték 8-szorosára növeli.

⋆

Az eredményhirdetésre és az ünnepélyes díjkiosztásra az ELTE új, lágymányosi épületének egyik nagyobb előadótermében került sor 1999. november 19-én. Itt először a Versenybizottság elnöke megemlékezett Sztrókay Pálról (1899‐1965) és Náray-Szabó Istvánról (1899‐1972), akik éppen száz évvel ezelőtt születtek, s az 1917. évi tanulóversenyen az 1. és 2. díjat nyerték. Sztrókay Pál Kossuth-díjas mérnök lett, a Ganznál a villamos vontatás fejlesztésén dolgozott, Kandó Kálmán utáni második emberként. Náray-Szabó István nemzetközi tekintélyű vegyészprofesszor lett, a fizika és a kémia határterületén alkotott: röntgendiffrakcióval kutatta az anyag kémiai-fizikai szerkezetét.
A rövid megemlékezések után került sor idei feladatok megoldásának diszkussziójára. Az első feladat megoldását Radnai Gyula, a másodikat az egyik versenyző (Tóth Bálint), a harmadikat Gnädig Péter mutatta be. A harmadik feladathoz kapcsolódóan, azt modellezve kísérleteket is láthattak a megjelentek: más-más falvastagságú, más-más fémből készült csöveknél különböző erősségű rúdmágnesek esési idejét figyelhették meg, s így összehasonlíthatták különféle körülmények között kialakuló örvényáramok fékező hatását.
Az ünnepélyes eredményhirdetésen Fehér István, az ELFT alelnöke adta át (a feladatok kitűzőiből álló) Versenybizottság által odaítélt díjakat. A Társulat által biztosított pénzjutalmak mellett a Nemzeti Tankönyvkiadótól könyvutalványokat kaptak a díjazott versenyzők, akiknek jelen levő tanárai a Műszaki Kiadó és a Tankönyvkiadó ajándék-könyveiből válogathattak. Sajnos nem mindenki tudott eljönni: az éppen a díjkiosztás napján kitört hóvihar miatt maradt le az ünnepségről néhány régi Eötvös-verseny nyertes is.

7. ábra

Az 1999. évi Eötvös-verseny díjazottai (fentről lefelé, balról jobbra): Péterfalvi Csaba Géza, Terpai Tamás, Gáspár Merse Előd, Buruzs Ádám, Katona Gergely, Csillag Kristóf, Hegedűs Ákos, Patay Gergely, Tóth Bálint, Pesti Gábor és Czigler István.

A mostani verseny eredménye a következő:

Első díjat kapott: Terpai Tamás, az ELTE matematikus hallgatója, aki a Fazakas Mihály Fővárosi Gyakorló Gimnáziumban érettségizett mint Horváth Gábor tanítványa.

Második díjat kapott a verseny 2‐6. helyezettje: Hegedűs Ákos, a pécsi ciszterci Nagy Lajos Gimnázium 12. osztályos tanulója, Orovica Márkné tanítványa; Katona Gergely, az ELTE fizikus hallgatója, aki a budapesti ELTE Trefort Ágoston Gyakorlóiskolában érettségizett mint Szörényi Zoltán tanítványa; Pesti Gábor, a nagykanizsai Batthyány Lajos Gimnázium 11. osztályos tanulója, Piriti János tanítványa; Péterfalvi Csaba Géza, az ELTE geofizikus hallgatója, aki a szekszárdi Garay János Gimnáziumban érettségizett mint Bayer József tanítványa; Tóth Bálint, az ELTE fizikus hallgatója, aki a Fazakas Mihály Fővárosi Gyakorló Gimnáziumban érettségizett mint Horváth Gábor tanítványa.

Harmadik díjat kapott a verseny 7‐10. helyezettje: Béky Bence, a Fazakas Mihály Fővárosi Gyakorló Gimnázium 10. osztályos tanulója, Horváth Gábor tanítványa; Csillag Kristóf, a püspökladányi Karacs Ferenc Gimnázium 12. osztályos tanulója, Lajtosné Buzási Márta tanítványa; Gáspár Merse Előd, a Fazakas Mihály Fővárosi Gyakorló Gimnázium 12. osztályos tanulója, Horváth Gábor tanítványa; Patay Gergely, a debreceni Tóth Árpád Gimnázium 12. osztályos tanulója, Kovács Miklós és Szegedi Ervin tanítványa.

Dicséretben részesült a verseny 11‐13. helyezettje: Buruzs Ádám, a szegedi Radnóti Miklós Gimnázium 12. osztályos tanulója, Mike János tanítványa; Czigler István, a budapesti Lauder Javne Gimnázium 12. osztályos tanulója, Tóth Eszter tanítványa; Kenyeres Péter, a POTE orvostanhallgatója, aki a zalaegerszegi Zrínyi Miklós Gimnáziumban érettségizett mint Pálovics Róbert tanítványa.
Az 1. díjas versenyző 10 000 Ft pénzjutalmat és 5 000 Ft értékű könyvutalványt, a 2. díjasok 6 000 Ft pénzjutalmat és 4 000 Ft értékű könyvutalványt, a 3. díjasok 4 000 Ft pénzjutalmat és 4 000 Ft értékű könyvutalványt, a dicséretben részesültek 3 000 Ft értékű könyvutalványt kaptak.
Gratulálunk a nyerteseknek és tanáraiknak!

Gnädig Péter, Radnai Gyula

¹Terpai Tamás dolgozata alapján

²Belátható, hogy ezt az általánosság megszorítása nélkül megtehetjük.