Kezdőlap


Cím:	Kepler egyenlete
Szerző(k):	Horányi Gábor
Füzet:	2000/február, 110 - 112. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A bolygók ‐ Kepler I. törvénye szerint ‐ olyan ellipszispályán mozognak, melynek egyik $(F)$ fókuszpontjában a Nap található. A bolygó pillanatnyi helyzete pl. az ábrán látható $α$ szöggel jellemezhető. A mozgás időbeli leírása, vagyis az $α$ szöghöz tartozó $C B$ ív befutásához szükséges idő megadása (a körpálya speciális esetét leszámítva) általában nem könnyű feladat.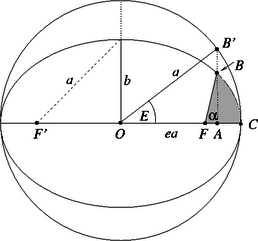

Kepler ‐ még a differenciálszámítás ismerete előtt ‐ levezetett egy olyan összefüggést, melynek segítségével kiszámítható egy tetszőleges ellipszis-ív befutásához szükséges idő. Az egyenlet Kepler II. törvényén, a területi sebesség állandóságán alapszik.
Tekintsünk egy

a

és

b

féltengelyű ellipszist, és használjuk az

\begin{matrix} e = \sqrt[]{1 - \frac{b^{2}}{a^{2}}}, \frac{b}{a} = \sqrt[]{1 - e^{2}} \end{matrix}

összefüggéseket. (

e

az ellipszis ,,excentricitása'', kör esetében

e = 0,

parabolává fajuló ,,ellipszisre'' pedig

e \to 1

.)
Nagyítsuk meg az ellipszist a kistengelye mentén

a / b

-szeresére, így egy

a

sugarú kört kapunk. Jelöljük a

B

helyen levő bolygónak megfelelő pontot a körön

B'

-vel, a

C O B'

szöget pedig

E

-vel. (Ezt a szöget az égi mechanikában excentrikus anomáliának nevezik.)
Kepler II. törvénye szerint a

B C

ív befutásához szükséges

t

idő úgy aránylik a

T

keringési időhöz, mint a vezérsugár által súrolt

A_{F C B}

terület (az ábrán satírozott rész területe) az ellipszis teljes területéhez. Ugyanez az arány a nagyítás után adódó körön is leolvasható:

\begin{matrix} \frac{t}{T} = \frac{A_{F C B'}}{a^{2} π} . \end{matrix}

Másrészt viszont az

A_{F C B'}

terület az

O C B'

körcikk

a^{2} E / 2

területének és az

O F B'

háromszög területének különbsége. Mivel az ellipszis középpontjának és a fókuszpontjának távolsága

\begin{matrix} O F = \sqrt[]{a^{2} - b^{2}} = a \sqrt[]{1 - \frac{b^{2}}{a^{2}}} = a \cdot e, \end{matrix}

O F B'

háromszög

B'

csúcsponthoz tartozó magassága pedig

a \cdot sin E,

felírhatjuk, hogy

\begin{matrix} \begin{matrix} \frac{t}{T} = \frac{\frac{1}{2} a^{2} E - \frac{1}{2} a e \cdot a sin E}{a^{2} π}, ahonnan t = T \frac{E - e sin E}{2 π} . \end{matrix} \end{matrix}

Ez Kepler egyenlete.
Az egyenlet gyakorlati alkalmazhatóságához meg kell határoznunk még a bolygó helyzetét jellemző

α

szög és az

E

szög közötti kapcsolatot. Elemi trigonometriai átalakítások segítségével belátható, hogy a kérdéses összefüggés a következő:

\begin{matrix} tg \frac{α}{2} = \sqrt[]{\frac{1 + e}{1 - e}} tg \frac{E}{2} . \end{matrix}

Tekintsük ugyanis az

F A B

háromszöget:

\begin{matrix} tg α = \frac{B A}{F A} = \frac{\sqrt[]{1 - e^{2}} \cdot B' A}{F A} = \frac{a sin E \sqrt[]{1 - e^{2}}}{a cos E - e a} = \frac{tg E \sqrt[]{1 - e^{2}}}{1 - e \sqrt[]{1 + tg^{2} E}} . \end{matrix}

Fennáll továbbá, hogy

\begin{matrix} tg α = \frac{2 tg \frac{α}{2}}{1 - tg^{2} \frac{α}{2}} és tg E = \frac{2 tg \frac{E}{2}}{1 - tg^{2} \frac{E}{2}}, \end{matrix}

amelyeket a fentebbi összefüggésbe helyettesítve némi átalakítás után

\begin{matrix} \frac{tg \frac{α}{2}}{1 - tg^{2} \frac{α}{2}} = \frac{\sqrt[]{\frac{1 + e}{1 - e}} tg \frac{E}{2}}{1 - \frac{1 + e}{1 - e} tg^{2} \frac{E}{2}} \end{matrix}

adódik. Jelöljük

tg \frac{α}{2}

-t

n

-nel,

\sqrt[]{\frac{1 + e}{1 - e}} tg \frac{α}{2}

-t pedig

m

-mel, akkor a fenti összefüggés így néz ki:

\begin{matrix} \frac{n}{1 - n^{2}} = \frac{m}{1 - m^{2}}, ahonnan (n - m) (1 + n m) = 0. \end{matrix}

Ez utóbbi viszont csak

n = m

, vagyis

\begin{matrix} tg \frac{α}{2} = \sqrt[]{\frac{1 + e}{1 - e}} tg \frac{E}{2} \end{matrix}

fennállása esetén teljesülhet, hiszen

n m

sosem negatív.
A fenti összefüggés segítségével adott

α

esetén könnyen kiszámíthatjuk az excentrikus anomáliát (

E

-t), abból pedig a

t

időt, így a

t (α)

függvényt, a bolygó mozgását megadó

α (t)

függvény inverzét.

Horányi Gábor