|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A csillagok egyik legfontosabb adata (állapotjelzője) a tömeg, meghatározása azonban csöppet sem egyszerű. Egy csillag tömegét megállapítani viszonylag megbízható pontossággal csak kettőscsillagok esetében lehetséges. Ilyenkor ugyanis a pályák adataiból a két csillag egymásra kifejtett gravitációs hatására lehet következtetni, ami viszont a tömegekkel arányos.
Tegyük föl, hogy egy kettőscsillag mindkét komponensét látjuk a távcsőben. Ha sokáig (esetenként több évtizeden vagy évszázadon keresztül) figyeljük a csillagpárt, megfigyelhető, hogyan mozdulnak el egymáshoz képest. Tudjuk, hogy mindkettő ellipszispályán mozog a rendszer tömegközéppontja körül, a tömegközéppont helyét azonban nem ismerjük. Egyszerűbbé teszi a helyzetet, ha az egyik csillagot (,,a főcsillagot'') rögzítettnek képzeljük, vagyis beülünk a főcsillaghoz rögzített koordináta-rendszerbe. Bebizonyítható, hogy a másik csillag ebből a (gyorsuló) koordináta-rendszerből nézve is ellipszispályán fog mozogni, s a pályaellipszis egyik fókuszpontjában a rögzítettnek tekintett csillag van.
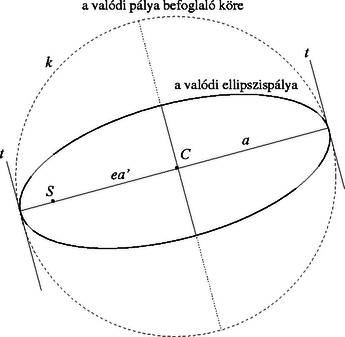
Legyen a főcsillag helye az pont, az észlelésekkel meghatározott pályaellipszis középpontja pedig (1. ábra)! Ez az ellipszis azonban még nem a 2. ábrán látható valódi pálya, hanem annak az éggömbre vetített képe, hiszen látóirányunk bizonyára nem merőleges a kettőscsillag keringési síkjára. Fontos megjegyezni, hogy az eredeti pályaellipszis fókuszpontjának éggömbre vetített képe, tehát a vetületi ellipszisnek nem fókuszpontja.
Határozzuk meg először az eredeti ellipszis nagytengelyének hosszát! A vetület azon átmérője, amelyre és illeszkedik, az eredeti pályaellipszis nagytengelyének vetülete, hiszen a párhuzamos vetítéssel a középpont középpontba ment át. Ezen átmérő feléből () és az távolságból kiszámíthatjuk az eredeti ellipszis pályaexcentricitását: A vetületi ellipszist a kistengely vetülete mentén -szeresre megnyújtva az eredeti pályaellipszis körülírható körének az éggömbre vonatkoztatott vetületét kapjuk meg. (A nyújtás iránya az 1. ábrán látható érintők irányával egyezik meg, hiszen a pályaellipszis nagytengelyének végpontjaiban húzható érintő (lásd a 2. ábrát) a kistengellyel párhuzamos.) Az így kapott ellipszis nagytengelye egyenlő lesz a valódi pályaellipszis körülírható körének átmérőjével, ami viszont a valódi pályaellipszis nagytengelyével egyenlő.
A leírt módszer az ún. Zwiers-féle grafikus eljárás, melyből az eredményt (a nagytengely méretét) még nem kilométerben, hanem csak a nagytengely látószögét (mondjuk ívmásodperc egységekben kifejezve) kapjuk meg. Ha ismerjük a kettős rendszer távolságát, akkor az adatot km-be is átszámíthatjuk; a gond azonban épp az szokott lenni, hogy ez a távolságadat nem áll rendelkezésünkre.
Ha a két csillag tömegközépponthoz viszonyított mozgását (pályaellipsziseik és nagytengelyeit) is mérni tudjuk, akkor ebből a két tömeg értékére a tömegközéppont megmaradásának tételéből újabb egyenlet adódik: Ezzel (és Kepler III. törvényével) már kiszámítható a két tömeg értéke.
A tömegek meghatározására az ún. dinamikus parallaxis-meghatározás a legszellemesebb eljárás, amely egyúttal a kettős távolságát is megadja. Ehhez ismernünk kell az előbbi eljárással meghatározott értéket, valamint három további egyenletet! Az első Kepler III. törvénye, amely szerint A második, az ún. empirikus tömeg-fényesség reláció azt az eredetileg tapasztalati úton megállapított, utóbb elméletileg is igazolt tényt rögzíti, hogy a legtöbb csillag esetén a fényesség (luminozitás, ) és a csillag tömege nem független egymástól, hanem Az összefüggést itt csak közelítő alakban írtuk föl, különböző csillagtípusokra ennél pontosabb alakja is ismeretes. Végül a harmadik a csillagok látszó és abszolút fényessége közti összefüggés: (A fenti egyenletekben a csillagok tömege, a tőlünk mért távolságuk parszek egységben, az abszolút fényesség, a megfigyelt keringési idő, a szintén közvetlenül mérhető látszó fényesség. Ha a Kepler-törvényben időegységnek az évet, távolságegységnek a csillagászati egységet, tömegegységnek a Nap tömegét vesszük, akkor a konstans értéke éppen 1.)
A számítás kezdetekor nem ismerjük sem a csillagok tömegét, sem távolságukat, de tudjuk, hogy a legtöbb csillag tömege és naptömeg közé esik. Vegyük első közelítésben mindkét csillag tömegét naptömegnek, ami bizonyára nem rossz közelítés; legyen tehát Ezeket a Kepler III. törvényébe helyettesítve megkapjuk a pálya a fél nagytengelyének hosszát csillagászati egységekben, vagy ha tetszik, km-ben. Ebből és a megfigyelt pályaadatokból (a Zwiers-féle grafikus eljárással) meghatározott látószögértékből kiszámíthatjuk a két csillag tőlünk mért távolságát, azaz értékét.
Ezután és az ismert látszó fényesség alapján meghatározzuk a két csillag fényességét. Mivel a két csillag látszó fényessége általában különböző, itt már két különböző és értéket kapunk, majd az empirikus tömeg-fényesség relációból meghatározzuk a két csillag és tömegét. Ezek most már különbözni fognak egymástól is, és az kiinduláskor feltételezett 1 naptömegnyi közelítő értéktől is.
Megkaptuk tehát a két csillag tömegének egy jobb közelítését. Ezeket ismét a Kepler-törvénybe helyettesítjük és elvégezzük újra az előbbi számításokat, így újabb, még pontosabb értékhez jutunk és így tovább. Néhány iterációs lépés után kielégítő pontosságú becslést kapunk a csillagok tömegére, és ‐ hasznos melléktermékként ‐ távolságukra is. (A módszer hibalehetősége többek között, hogy az abszolút és a látszó fényesség összefüggése nem tartalmazza a csillagközi fényelnyelés ‐ általában ismeretlen ‐ mértékét, amely a távolság növekedésével egyre bizonytalanabbá teszi az abszolút fényességre kapott eredményt.)
Ha egy csillag távolságát valahonnan már ismerjük (pl. geometriai parallaxisát sikerült meghatározni), akkor egyszerűbben is eljárhatunk. Látszó fényességéből és távolságából kiadódik a csillag fényessége, ebből és a tömeg-fényesség relációból pedig megbecsülhető a tömege.
|
 PDF | MathML
PDF | MathML