Cím:	A 31. Nemzetközi Fizikai Diákolimpia feladatainak megoldása
Szerző(k):	Gnädig Péter ,  Vankó Péter
Füzet:	2000/november, 495 - 505. oldal	PDF  |  MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1   Elméleti forduló       1. feladat. Néhány (egymástól független) probléma.   A) a) A ,,halálugró'' ember sebessége akkor csökken először nullára, amikor a gravitációs helyzeti energia csökkenése megegyezik a kötélben tárolt rugalmas energiával: $\begin{array}{c}{\displaystyle mgy=\frac{1}{2}k{\left(y-L\right)}^2\mathrm{.}}\end{array}$ Ennek a másodfokú egyenletnek a megoldásai: $\begin{array}{c}{\displaystyle y=\frac{kL+mg\pm \sqrt[]{2mgkL+m^2{g}^2}}{k}\mathrm{.}}\end{array}$ Esetünkben a gyökjel előtt a negatív előjelet kell választanunk, hiszen az alacsonyabb helyzetű (nagyobb $y$-hoz tartozó) egyensúlyi helyzetet keressük.   b) Az ugró ember sebessége akkor maximális, amikor a gyorsulása nulla, vagyis amikor az erőegyensúly $mg=kx$ feltétele teljesül. Ebben a pillanatban a munkatétel szerint $\begin{array}{c}{\displaystyle \frac{1}{2}m{v}_{\text{max}}^2=mg\left(L+x\right)-\frac{1}{2}k{x}^2\mathrm{,}}\end{array}$ ahonnan $x=mg/k$ felhasználásával a kérdéses sebesség $\begin{array}{c}{\displaystyle v_{\text{max}}=\sqrt[]{2gL+\frac{m{g}^2}{k}}\mathrm{.}}\end{array}$   c) Az ugró ember első megállásáig eltelő idő két tag összegeként számítható ki: a kötél megfeszüléséig a mozgás szabadesés, ennek időtartama $t_1=\sqrt[]{2L/g}\mathrm{,}$ majd az ezt követő harmonikus rezgőmozgás bizonyos szakaszának $t_2$ ideje együtt teszi ki a kérdéses időtartamot. A harmonikus rezgőmozgás periódusideje $T=2\pi \sqrt[]{m/k}$, körfrekvenciája $\omega =\sqrt[]{k/m}$. A sebesség időbeli változása $\begin{array}{c}{\displaystyle v\left(t\right)=v_{\text{max}}\text{sin}\left(\omega t\right)}\end{array}$ alakban írható fel, kezdetét pedig az a $\tau$ időpillanat jellemzi, melynél a rezgő test sebessége éppen megegyezik a szabadesés végsebességével, vagyis a $v_{\tau }=g{t}_1=\sqrt[]{2gL}$ mennyiséggel (1. ábra). Innen $\begin{array}{c}{\displaystyle \tau =\frac{1}{\omega }\text{arc}\text{sin}\frac{\sqrt[]{2gL}}{v_{\text{max}}}\mathrm{,}}\end{array}$ az esés teljes ideje pedig az első megállásig $\begin{array}{c}{\displaystyle t_{\text{teljes}}=t_1+t_2=t_1+\left(\frac{T}{2}-\tau \right)=\sqrt[]{\frac{2L}{g}}+\sqrt[]{\frac{m}{k}}\left(\pi -\text{arc}\text{sin}\frac{\sqrt[]{2gL}}{\sqrt[]{2gL+m{g}^2/k}}\right)\mathrm{.}}\end{array}$   1. 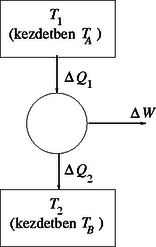ábra   B) Jelöljük az $A$ test által leadott hőt $\Delta Q_1$-gyel, a $B$ test által felvett hőt pedig $\Delta Q_2$-vel. Ezeket a mennyiségeket kifejezhetjük a megfelelő hőmérsékletváltozásokkal: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle \Delta Q_1=-ms\Delta T_1\mathrm{,}\Delta T_1\text{negatív}\mathrm{,}}\\ \hfill {\displaystyle \Delta Q_2=ms\Delta T_2\mathrm{,}\Delta T_2\text{pozitív}\mathrm{.}}\end{array}}}\end{array}$   2. ábra   a) A hőerőgép akkor végzi a lehető legtöbb munkát, ha Carnot-gépként működik. Ilyenkor $\begin{array}{c}{\displaystyle \frac{\Delta Q_1}{T_1}=\frac{\Delta Q_2}{T_2}\mathrm{,}}\end{array}$ vagyis $\begin{array}{c}{\displaystyle -ms\frac{\Delta T_1}{T_1}=ms\frac{\Delta Q_2}{T_2}\mathrm{.}}\end{array}$ Ez az összefüggés $\begin{array}{c}{\displaystyle T_1\cdot \Delta T_2+T_2\cdot \Delta T_1=\Delta \left(T_1\cdot T_2\right)=\mathrm{0,}}\end{array}$ tehát $T_1\cdot T_2=\text{állandó}$ alakba is írható. Eszerint a végső (közös) hőmérséklet: $T_0=\sqrt[]{T_A{T}_B}\mathrm{.}$ Ugyanez az eredmény integrálszámítással is megkapható: $\begin{array}{c}{\displaystyle -ms\underset{T_A}{\overset{T_0}{\int }}\frac{d{T}_1}{T_1}=ms\underset{T_B}{\overset{T_0}{\int }}\frac{d{T}_2}{T_2}\mathrm{,}}\end{array}$ ahonnan $\text{ln}\left(T_A/T_0\right)=\text{ln}\left(T_0/T_B\right)\mathrm{,}$ vagyis $T_0=\sqrt[]{T_A{T}_B}$ következik.   b) A munkavégzés a leadott és a felvett hő különbségéből számítható: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle W=Q_1-Q_2=ms\left(T_A-T_0\right)-ms\left(T_0-T_B\right)=}\\ \hfill {\displaystyle =ms\left(T_A+T_B-2T_0\right)=ms{\left(\sqrt[]{T_A}-\sqrt[]{T_B}\right)}^2\mathrm{.}}\end{array}}}\end{array}$   c) A megadott számadatokkal $W=20$ MJ.   C) a) A kezdetben $N_0$ darab ${}^{238}\text{U}$ izotópból $t$ idő múlva már csak $N=N_0{e}^{-\lambda t}$ marad, tehát a bomlástermékének száma $n=N_0\left(1-e^{-\lambda t}\right)=N\left(e^{\lambda t}-1\right)\mathrm{.}$ Mivel a $\lambda$ bomlásállandó és a $T$ felezési idő közötti kapcsolat: $\lambda =\frac{\text{ln}2}{T}=\frac{0\mathrm{,}693}{T}\mathrm{,}$ az ${}^{238}\text{U}$ atomok pillanatnyi ${}^{238}N$ száma és a bomlása során keletkező ${}^{206}\text{Pb}$ atomok pillanatnyi ${}^{206}n$ száma közötti kapcsolat (ha az időt milliárd év egységekben mérjük): $\begin{array}{c}{\displaystyle {}^{206}n={}^{238}N\left(e^{0\mathrm{,}154t}-1\right)={}^{238}N\left(2^{t/4\mathrm{,}50}-1\right)\mathrm{.}}\end{array}$   b) Hasonlóan az előbbi pontban leírtakhoz $\begin{array}{c}{\displaystyle {}^{207}n={}^{235}N\left(e^{0\mathrm{,}976t}-1\right)={}^{235}N\left(2^{t/0\mathrm{,}710}-1\right)\mathrm{.}}\end{array}$   c) Az urán-ólom keverékben (ahol a radioaktív bomlások során folyamatosan keletkeznek ólom atomok), a különböző tömegszámú ólomizotópok számának aránya: $\begin{array}{c}{\displaystyle 204:206:207\Rightarrow 1\mathrm{,}00:29\mathrm{,}6:22\mathrm{,}6.}\end{array}$ A tiszta ólomban a megfelelő arányok: $\begin{array}{c}{\displaystyle 204:206:207\Rightarrow 1\mathrm{,}00:17\mathrm{,}9:15\mathrm{,}5.}\end{array}$ A fenti arányszámok különbségét képezve látható, hogy a radioaktív bomlásokból származó ólomizotópok aránya: $\begin{array}{c}{\displaystyle 206:207\Rightarrow 11\mathrm{,}7:7\mathrm{,}1.}\end{array}$ Az $a)$ és a $b)$ alkérdések megoldásában szereplő egyenlőségek hányadosát képezve: $\begin{array}{c}{\displaystyle \frac{{}^{206}n}{{}^{207}n}=\frac{{}^{238}N}{{}^{235}N}\frac{e^{0\mathrm{,}154t}-1}{e^{0\mathrm{,}976t}-1}\mathrm{,}}\end{array}$ ahonnan a Föld $T$ életkorára a következő egyenletet kapjuk: $\begin{array}{c}{\displaystyle \frac{11\mathrm{,}7}{7\mathrm{,}1}=137\frac{e^{0\mathrm{,}154T}-1}{e^{0\mathrm{,}976T}-1}\mathrm{,}}\end{array}$ vagyis $\begin{array}{c}{\displaystyle 0\mathrm{,}012\left(e^{0\mathrm{,}976T}-1\right)=\left(e^{0\mathrm{,}154T}-1\right)\mathrm{.}}\end{array}$   d) Feltételezve, hogy $T\gg 4\mathrm{,}5\cdot {10}^9$ év, a fenti formulában a zárójelekben az 1-eseket elhanyagolhatjuk, s $T$-t könnyen kifejezhetjük (milliárd években): $\begin{array}{c}{\displaystyle T=\frac{\text{ln}0\mathrm{,}012}{-0\mathrm{,}822}=5\mathrm{,}38.}\end{array}$   e) Láthatjuk, hogy ez a közelítő érték nem sokkal nagyobb, mint a hosszabb felezési idő (tehát a kiszámítása során alkalmazott elhanyagolás nem volt jogos!), de felhasználható egy pontosabb $T$ érték meghatározására. Jelöljük a Föld életkorára durva közelítésben kapott 5,38 milliárd évet $T^{*}$-gal, s az eredeti egyenlet helyett tekintsük a $\begin{array}{c}{\displaystyle 0\mathrm{,}012\left(e^{0\mathrm{,}976T}-1\right)=\left(e^{0\mathrm{,}154T^{*}}-1\right)}\end{array}$ egyenletet. Ez zárt alakban megoldható, s $T$-re $4\mathrm{,}80\cdot {10}^9$ év adódik. Ha ezen értéket írjuk $T^{*}$ helyébe, $T$-re még jobb közelítést, $4\mathrm{,}62\cdot {10}^{10}$ évet kapunk. Ezt a (fokozatosan közelítő) eljárást tovább folytatva az eredmények $4\mathrm{,}52\cdot {10}^9$ évhez konvergálnak. (Ezt a gyököt természetesen más módszerekkel, pl. az eredeti exponenciális egyenlet grafikus megoldásával is megkaphatjuk.)   D) A homogén töltéseloszlású gömb elektromos töltéssűrűsége: $\begin{array}{c}{\displaystyle \varrho =\frac{Q}{\frac{4}{3}\pi R^3}\text{(ha}r<R)\mathrm{.}}\end{array}$   a) Az elektromos térerősség a gömb középpontjától mért $r$ távolságban $r\le R$ esetén az $r$ sugarú gömbben levő töltések Coulomb-terével, $r\ge R$ esetben pedig a teljes $Q$ töltés Coulomb-terével egyezik meg: $\begin{array}{c}{\displaystyle E=\{{\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{\frac{4}{3}\pi r^3\varrho }{4\pi {\epsilon }_0{r}^2}=\frac{Qr}{4\pi {\epsilon }_0{R}^3}\mathrm{,}}& {\displaystyle \text{ha <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>r</mi><mo>≤</mo><mi>R</mi></math>;}}\hfill \\ \multicolumn{2}{c}{\text{<div style="line-height: 6pt"> </div>}}\\ \hfill {\displaystyle \frac{Q}{4\pi {\epsilon }_0{r}^2}\mathrm{,}}& {\displaystyle \text{ha <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>r</mi><mo>≥</mo><mi>R</mi></math>.}}\hfill \end{array}}}\end{array}$   b) A teljes elektromos mező $W$ energiája az elektromos mező térerősségének ismeretében gömbhéjak energiájából integrálható össze: $\begin{array}{c}{\displaystyle W=\underset{0}{\overset{\infty }{\int }}\frac{1}{2}{\epsilon }_0{E}^2\cdot 4\pi r^{2}dr=\frac{Q^2}{8\pi {\epsilon }_0}\left(\frac{1}{R^6}\underset{0}{\overset{R}{\int }}{r}^{4}dr+\underset{R}{\overset{\infty }{\int }}\frac{1}{r^2}dr\right)=\frac{3}{20}\frac{Q^2}{\pi {\epsilon }_{0}R}\mathrm{.}}\end{array}$ A teljes energiát úgy is ki lehet számítani, hogy meghatározzuk, mekkora munkavégzéssel lehet vékony, egyenletesen töltött gömbhéjakban található töltéseket nagyon messziről (a ,,végtelenből'') $r$ sugárnak megfelelő helyzetbe hozni, miközben $r$ fokozatosan nő 0-tól $R$-ig. Mivel $r$ sugarú homogénen töltött gömb felületén az elektromos potenciál $\begin{array}{c}{\displaystyle U\left(r\right)=\frac{\frac{4}{3}\pi r^3\varrho }{4\pi {\epsilon }_{0}r}=\frac{r^2\varrho }{3{\epsilon }_0}\mathrm{,}}\end{array}$ így a teljes munka $\begin{array}{c}{\displaystyle W=\underset{0}{\overset{R}{\int }}}\end{array}$ r2ϱ3ε0⋅4πr2ϱdr=4πϱ23ε0∫0Rr4dr=4πϱ23ε0R55=320Q2πε0R.   E) A mágneses indukcióvektor vízszintes komponense $\begin{array}{c}{\displaystyle B=44\mathrm{,}5\mu \text{T}\cdot \text{cos}{64}^{\circ }\mathrm{,}}\end{array}$ amely az $a$ sugarú, $\theta$ szöggel jellemezhető síkban álló rézgyűrűn keresztül $\begin{array}{c}{\displaystyle \Phi =B{a}^2\pi \text{sin}\theta }\end{array}$ mágneses fluxust eredményes. Ha a gyűrű $\omega$ szögsebességgel (közel egyenletesen) forog, a benne indukálódó pillanatnyi feszültség (elektromotoros erő) $\begin{array}{c}{\displaystyle U\left(t\right)=\frac{d\Phi }{dt}=B{a}^2\pi \frac{d}{dt}\text{sin}\omega t=B{a}^2\pi \omega \text{cos}\omega t\mathrm{.}}\end{array}$ Ez a változófeszültség a hőhatását tekintve $\begin{array}{c}{\displaystyle U_{\text{eff}}=\frac{1}{\sqrt[]{2}}{U}_{max}=\frac{B{a}^2\pi \omega }{\sqrt[]{2}}}\end{array}$ effektív feszültséggel egyenértékű, tehát az $R$ ellenállású rézgyűrűben átlagosan $\begin{array}{c}{\displaystyle P=\frac{U_{\text{eff}}^2}{R}=\frac{B^2{\pi }^2{a}^4{\omega }^2}{2R}}\end{array}$ teljesítménnyel termel hőt, s ugyanilyen mértékben csökkenti időegységenként az $m$ tömegű, az átmérőjére vonatkoztatva $\Theta =\frac{1}{2}m{a}^2$ tehetetlenségi nyomatékú gyűrű mechanikai (forgási) energiáját: $\begin{array}{c}{\displaystyle P=-\frac{d}{dt}\left(\frac{1}{4}m{a}^2{\omega }^2\right)=-\frac{1}{2}m{a}^2\omega \frac{d\omega }{dt}\mathrm{.}}\end{array}$ Ezek szerint a szögsebesség (lassú) változását megadó egyenlet: $\begin{array}{c}{\displaystyle \frac{d\omega \left(t\right)}{dt}=-\lambda \cdot \omega \left(t\right)\mathrm{,}}\end{array}$ ahol $\lambda =B^2{\pi }^2{a}^2/\left(mR\right)$ állandó, amely a réz $s$ sűrűségével és $\varrho$ fajlagos ellenállásával is kifejezhető: $\lambda =B^2/\left(4s\varrho \right)$. Ez az egyenlet (differenciálegyenlet) alakilag megegyezik a radioaktív bomlások egyenletével, tehát a megoldása is azokéval egyező: $\begin{array}{c}{\displaystyle \omega \left(t\right)={\omega }_0{e}^{-\lambda t}\mathrm{.}}\end{array}$ A szögsebesség felezési ideje (tehát az a $T_{1/2}$ idő, amikor $\omega \left(t\right)={\omega }_0/2$: $T_{1/2}=\frac{\text{ln}2}{\lambda }=\frac{4\text{ln}2s\varrho }{B^2}\mathrm{,}$ ami a megadott számadatokkal $1\mathrm{,}10\cdot {10}^6\text{s}\approx 306$ óra$\approx 13$ napnak adódik. Az eredmény a szögsebesség változását megadó egyenletből integrálszámítással is megkapható: $\begin{array}{c}{\displaystyle \frac{d\omega \left(t\right)}{dt}=-\lambda \cdot \omega \left(t\right)\Rightarrow \underset{{\omega }_0}{\overset{{\omega }_0/2}{\int }}\frac{d\omega }{\omega }=-\lambda \underset{0}{\overset{T_{1/2}}{\int }}dt\Rightarrow \text{ln}2=\lambda T_{1/2}\mathrm{.}}\end{array}$ A rézgyűrű fékeződése más módszerrel, pl. a gyűrűre ható átlagos forgatónyomaték kiszámításával, majd a forgómozgás dinamikai egyenletének felírásával és megoldásával is meghatározható.     2. feladat. Az elektron fajlagos töltésének meghatározása.   a) Az elektron sebessége $V$ gyorsítófeszültség esetén $v=\sqrt[]{2eV/m}\mathrm{,}$ ahol $e/m$ a kérdéses fajlagos töltés. (Felhasználtuk, hogy az elektron gyorsítása során szerzett $eV$ energia sokkal nagyobb, mint az elektron kezdeti mozgási energiája, de sokkal kisebb, mint az elektron nyugalmi energiája, így nincs szükség relativisztikus mozgástörvények használatára.) Az elektronok a katód és az anód közötti $D$ távolságot $T=D\text{cos}\beta /v\approx D/v$ idő alatt teszik meg, miközben a mágneses tér miatt a tengelyre merőleges síkban $\omega =eB/m$ szögsebességgel (az ún. ciklotronfrekvenciával) körmozgást végeznek. A különböző irányban induló elektronok akkor fókuszálódnak az ernyőn (akkor csapódnak be közel azonos helyen), ha a $T$ repülési idő alatt a ciklotronfrekvenciájú körmozgásban éppen egész számú kört tesznek meg. A legkisebb fókuszáló mágneses mezőben 1 kör megtételére van idő, vagyis $T=1\cdot \left(2\pi /\omega \right)\mathrm{.}$ Ennek feltétele: $\begin{array}{c}{\displaystyle \frac{D}{\sqrt[]{2eV/m}}=2\pi \frac{m}{eB}\mathrm{,}\text{azaz}\frac{e}{m}=\frac{8{\pi }^{2}V}{B^2{D}^2}\mathrm{.}}\end{array}$   b) Az elektronok akkor juthatnak csak ki az egymáshoz igen közeli lemezek közül (akkor nem ütköznek bele egyikbe sem), ha a lemezekre merőleges irányban ható eredő erő (az elektromos mezőből és a mágneses mezőből származó erők összege) éppen nulla. Tekintsük azt az esetet, amikor $V>0$ és $B>0$. Ilyenkor a felső lemez pozitív, tehát a negatív töltésű elektronokra az elektromos mező felfele mutató erőt fejt ki. Az $A$ tartományban (az óramutató járásával ellentétesen kanyarodó elektronoknál) a Lorentz-erő ugyancsak felfele mutat, ezek az elektronok tehát a felső lemezbe ütköznek, nem érhetik el a filmet. A $B$ tartományban az elektromos mező és a mágneses mező ellentétes irányú erőt fejt ki, ezek tehát (megfelelő nagyságú sebességgel mozgó elektronoknál) kiejtheti egymást. A film tehát az $B$ tartományban készült. Ugyanezt állíthatjuk akkor is, ha $B$ és $V$ előjele negatív, hiszen ilyenkor mind az elektromos, mind pedig a mágneses erő az előzőhöz képest ellentétes irányú.   c) Itt is az elektromos és a mágneses erők egyenlőségét kell megkövetelnünk. Az elektromos mező által kifejtett erő nagysága: $eV/t$, a mágneses mezőé pedig $evB\text{sin}\varphi$, ahol $v$ az elektron sebessége. Az erőegyensúly feltétele: $\begin{array}{c}{\displaystyle v=\frac{V}{tB\text{sin}\varphi }\mathrm{.}}\end{array}$ A legnagyobb részecskesebesség a legkisebb megfigyelt szögnek, ${\varphi }_{\text{min}}={23}^{\circ }$-nak felel meg: $\begin{array}{c}{\displaystyle v_{\text{max}}=2\mathrm{,}687\cdot {10}^8\text{m/s}=0\mathrm{,}896c\mathrm{.}}\end{array}$ Ez már a fénysebességgel összemérhető, a mozgási energiát tehát a $\begin{array}{c}{\displaystyle W_{\text{mozgási}}=W_{\text{teljes}}-W_{\text{nyugalmi}}=\frac{m{c}^2}{\sqrt[]{1-v^2/c^2}}-m{c}^2}\end{array}$ relativisztikus képletekből kell számítanunk. Numerikusan: $W_{\text{mozgási}}=641\text{keV}\mathrm{.}$   d) A lemezek közötti térrészt elhagyva az elektronokra már csak a mágneses mezőtől származó (jó közelítéssel függőleges irányúnak tekinthető), $evB\text{sin}\varphi$ nagyságú Lorentz-erő hat. Az ettől származó gyorsulás (a relativisztikus tömegnövekedést is figyelembe véve) $\begin{array}{c}{\displaystyle a=evB\text{sin}\varphi \cdot \frac{\sqrt[]{1-v^2/c^2}}{m}\mathrm{,}}\end{array}$ a függőleges elmozdulás tehát (a feladat szövegében megadott 3. és 5. ábrák jelöléseit használva) $\begin{array}{c}{\displaystyle \frac{y}{2}=\frac{a}{2}{\tau }^2\mathrm{,}}\end{array}$ ahol $\tau =s/v$ a repülés ideje. Másrészt viszont $v$ kifejezhető a $\varphi$ szöggel (lásd az előző alkérdést), így végül $y$ és $\varphi$ között az alábbi összefüggést kapjuk: $\begin{array}{c}{\displaystyle y^2={\left(\frac{esB\text{sin}\varphi }{m}\right)}^2\left[{\left(\frac{Bst\text{sin}\varphi }{V}\right)}^2-{\left(\frac{s}{c}\right)}^2\right]\mathrm{.}}\end{array}$ Ezek után ha ábrázoljuk milliméterpapíron ${\displaystyle (}\frac{y}{Bs\text{sin}\varphi }{)}^2$-t ${\displaystyle (}\frac{Bst\text{sin}\varphi }{V}{)}^2$ függvényében, közelítőleg egyenest kell kapjunk, melynek meredeksége ${\left(e/m\right)}^2$, tengelymetszete pedig $-{\left[es/\left(mc\right)\right]}^2$. Mindkét mennyiség leolvasható a grafikonról, és a keresett fajlagos töltésre a meredekségből $e/m=1\mathrm{,}70\cdot {10}^{11}$ C/kg, a tengelymetszetből pedig $e/m=1\mathrm{,}68\cdot {10}^{11}$ C/kg adódik. (Az elektron fajlagos töltését elsőként J.J.Thomson angol fizikus mérte meg 1897-ben, mai ,,hivatalosan elfogadott'' értéke $e/m=1\mathrm{,}76\cdot {10}^{11}$ C/kg.)     3. feladat. Gravitáciás hullámok és a gravitáció hatása a fényre.   A) a) A rudak szabad végeinek rezgését leíró $\Delta x_t\propto e^{-\mu t}$ függvényben az exponenciális faktor 50 s alatt $20\%$-kal csökken, tehát $0\mathrm{,}8=e^{-\mu \cdot 50\text{s}}\mathrm{,}$ ahonnan $\mu =4\mathrm{,}5\cdot {10}^{-3}\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>s</mi></mrow><mrow><mo stretchy="false">-</mo><mn>1</mn></mrow></msup></mrow></math>}$.   b) A longitudinális hullámok sebessége az alumínium megadott anyagi állandóiból számítható: $v=\sqrt[]{E/\varrho }=5100$ m/s. Tudjuk továbbá, hogy az egyik végén rögzített, a másik végén szabadon mozgó rúd longitudinális alaprezgésénél a rúd hossza a hullámhossz negyede, vagyis ${\lambda }_{\text{rúd}}=4\ell =4$m, alaprezgés frekvenciája tehát $f=v/\lambda =1\mathrm{,}3$kHz, körfrekvenciája pedig $\omega =2\pi f=8\mathrm{,}1\cdot {10}^3\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>s</mi></mrow><mrow><mo stretchy="false">-</mo><mn>1</mn></mrow></msup></mrow></math>.}$   c) A rudak hossza és a rezgések frekvenciája fordítottan arányos egymással: $\ell \cdot f=v/4=$állandó, vagyis $\begin{array}{c}{\displaystyle \frac{\Delta \ell }{\ell }=-\frac{\Delta f}{f}=\frac{5\cdot {10}^{-3}}{1\mathrm{,}3\cdot {10}^3}=3\mathrm{,}8\cdot {10}^{-6}\mathrm{.}}\end{array}$ A két (közelítőleg 1 méteres) rúd hosszának különbsége tehát $3\mathrm{,}8$ mikron.   d) A gravitációs térerősség (gravitációs gyorsulás) hatására egy $\ell$ hosszúságú, $\varrho$ sűrűségű rúd rögzített végénél $\sigma =\ell g\varrho$ rugalmas feszültség ébred, a szabad végénél nulla a feszültség, az átlagos feszültség tehát $\overline{\sigma }=\frac{1}{2}\ell g\varrho$. Ennek hatására a rúd deformációja $\begin{array}{c}{\displaystyle \frac{\ell \overline{\sigma }}{E}=\frac{{\ell }^2\varrho }{2E}\cdot g\mathrm{,}}\end{array}$ amelynek kicsiny megváltozása a gravitációs térerősség kicsiny $\Delta g$ megváltozásának hatására $\begin{array}{c}{\displaystyle \Delta \ell =\frac{{\ell }^2\varrho }{2E}\cdot \Delta g\mathrm{.}}\end{array}$   e) A $\Delta \ell =656\text{nm}\cdot {10}^{-4}=\frac{{\ell }^2\varrho }{2E}\cdot \Delta g$ összefüggésből a megadott számadatokkal a szükséges rúd hosszára $\ell \approx 2\cdot {10}^8$ m adódik. Ilyen hosszú (csillagászati méretű) rúd nyilvánvalóan nem készíthető! A számítás eredménye mindenesetre tanulságos, rávilágít arra a tényre, hogy a gravitációs hullámok kísérleti kimutatása technikailag igen nehéz feladat, nem csoda, hogy mind ez ideig még nem sikerült. Megjegyzés. A fenti becslésnél azt tételeztük fel, hogy a gravitációs térerősség egy igen kicsit megváltozik, majd stabilan a megváltozott érték marad; emiatt az egyik rúd szabad vége kicsit elmozdul. A reálisan várható mérési elrendezésben $\Delta g$ csak egy nagyon rövid ideig különbözik nullától (hiszen a gravitációs hullámok fénysebességgel terjednek), s csak ,,meglökik'' a rudat, amely (kicsiny csillapítás esetén) az alaprezgés frekvenciájával hosszú ideig tartó rezgésbe kezd. A tervezett mérésekben ennek a rezgésnek közvetett hatásait szeretnék kimutatni.   B) Gravitációs mező hatása a fény terjedésére az űrben   a) A $hf=m{c}^2$ összefüggésből az $f$ frekvenciájú foton ,,ekvivalens tömege'' $m=hf/c^2\mathrm{.}$ A Nap felszínéről induló és onnan nagyon messze eltávolodó foton mozgási energiája a gravitációs helyzeti energia változása miatt $hf\text{'}=hf-GmM/R$ értékű lesz, ahonnan a bizonyítandó $f\text{'}=f\left(1-GM/R{c}^2\right)$ formulát kapjuk.   b) Ha a gravitációs mező jelenléte a Nap középpontjától $r$ távolságban a frekvenciákat és a távolságokat $\left(1-GM/R{c}^2\right)$ arányban csökkenti, az időtartamokat pedig ugyanilyen mértékben növeli, akkor ez a fény terjedési sebességének ${\left(1-GM/R{c}^2\right)}^2$ arányú csökkenéséhez vezet. Ezek szerint az effektív törésmutató $\begin{array}{c}{\displaystyle n_r=\frac{c}{c\text{'}}={\left(1-\frac{GM}{r{c}^2}\right)}^{-2}\approx 1+2\cdot \frac{GM}{r{c}^2}\mathrm{,}}\end{array}$ vagyis a kérdéses $\alpha$ állandó számértéke 2.   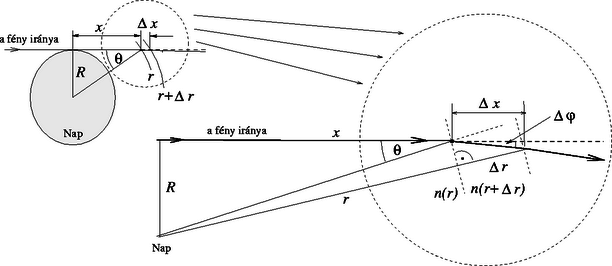c) A Nap szélét éppen érintő fénysugár a gravitáció hatására ‐ a fentebb kiszámított, helyről helyre változó effektív törésmutató miatt ‐ fokozatosan elgörbül. Osszuk fel a fénysugár pályáját a Napot érintő pontjától mért $x$ távolság függvényében kicsiny szakaszokra. Az $x$ és $x+\Delta x$ radiális távolsággal jellemzett pontok közötti gömbhéjat tekintsük optikailag homogén, $n\left(r+\Delta r\right)$ törésmutatójú közegnek, az alatta levő réteget pedig $n\left(r\right)$ törésmutatójúnak (lásd a 3. ábrát)! A réteg alsó határfelületére eső fénysugár a Snellius‐Descartes-törvénynek megfelelően megtörik, eredeti irányához képest igen kicsiny $\Delta \phi$ szöggel eltérül:   3. ábra   $\begin{array}{c}{\displaystyle \frac{\text{sin}\theta }{\text{sin}\left(\theta +\Delta \phi \right)}=\frac{n\left(r+\Delta r\right)}{n\left(r\right)}\mathrm{.}}\end{array}$ Használjuk ki, hogy $\Delta \phi$ és $\Delta r=\Delta x\text{cos}\theta$ kicsiny mennyiségek, továbbá hogy $n\left(r\right)\approx 1$ miatt a fény pályája alig tér el az egyenestől, így $\begin{array}{c}{\displaystyle \text{sin}\left(\theta +\Delta \phi \right)\approx \text{sin}\theta +\Delta \phi \text{cos}\theta }\end{array}$ és $\begin{array}{c}{\displaystyle n\left(r+\Delta r\right)-n\left(r\right)=\frac{2GM}{c^2}\left(\frac{1}{r+\Delta r}-\frac{1}{r}\right)\approx -\frac{2GM}{r^2{c}^2}\Delta r\mathrm{,}}\end{array}$ ahonnan a szögeltérülésre $\begin{array}{c}{\displaystyle \Delta \phi =\frac{2GM}{r^2{c}^2}\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\theta \cdot \Delta r=\frac{2GMR}{c^2}\cdot \frac{\Delta x}{{\left(x^2+R^2\right)}^{3/2}}}\end{array}$ adódik. összegezve (integrálva) ezt az összefüggést (az $x$ változóra teljes tartományára) megkapjuk a fény teljes eltérülését: $\begin{array}{c}{\displaystyle \phi =\frac{2GMR}{c^2}\underset{-\infty }{\overset{\infty }{\int }}\frac{dx}{{\left(x^2+R^2\right)}^{3/2}}=\frac{4GM}{R{c}^2}\approx 8\mathrm{,}4\cdot {10}^{-6}\text{<span style="font-weight: normal;font-style: normal;">radián</span>}\mathrm{.}}\end{array}$ Megjegyzés. A feladat megoldása során követett gondolatmenet a klasszikus newtoni gravitációelmélet fogalmait használja (némi relativisztikus korrekcióval). Ez a leírás nem minden esetben tükrözi helyesen a kísérletileg megfigyelt tényeket; erre mai tudásunk szerint csak az Einstein-féle általános relativitáselmélet képes, melynek matematikai apparátusa és fogalomrendszere azonban sokkal bonyolultabb annál, semhogy középiskolás versenyfeladatok között felhasználható volna. A diákolimpián szereplő (a gravitációs fényelhajlást tárgyaló) feladatban a ,,félklasszikus'' gondolatmenettel kapott formula megegyezik az általános relativitáselmélet (kísérletek által is pontosan igazolt) jóslatával, a gravitációs hullámok Einstein-féle elmélete azonban sokkal összetettebb, mint azt a versenyfeladat megoldása alapján vélhetnénk. Gnädig Péter     Kísérleti forduló     CD-ROM spektrométer.   Ebben a feladatban a versenyzőknek egy pontosan lépésekre tagolt, részletesen leírt mérést kellett végrehajtaniuk. A kihívás inkább a mérés gyors és pontos elvégzése volt. A meghajlított CD-darabbal könnyen elő lehetett állítani az elsőrendű spektrumot, és a fotóellenállás fókuszsíkban való mozgatásával a karakterisztikát (a vezetőképességet a hullámhossz függvényében) sem volt nehéz kimérni. A hullámhosszakat a megadott rácsállandóból és a geometriai adatokból lehetett kiszámítani. Bár csak a látható tartományban kellett mérni, és így a színek támpontot adtak a hullámhosszak körülbelüli értékére, mégis előfordult nagyságrendi hiba is a hullámhosszak meghatározásánál. A mérés másik felében ezt a kimért, elsődleges karakterisztikát kellett korrigálni, hiszen a spektrum létrehozásához használt izzó nem azonos intenzitással sugároz a különböző hullámhosszakon. Először azt kellett igazolni, hogy az izzó abszolút fekete testként viselkedik: ehhez az izzólámpa feszültsége és árama között fennálló $U^3\propto I^5$ összefüggés kísérleti igazolására volt szükség. Ezután az izzó ,,meleg-'' és ,,hideg-ellenállása'' alapján meg kellett mérni az izzószál hőmérsékletét. (A volfrám fajlagos ellenállásának hőmérsékletfüggését megadták.) A feladatot az tette bonyolultabbá, hogy az izzó ellenállása szobahőmérsékleten olyan kicsi, hogy a rendelkezésre álló műszerekkel nem lehetett elegendő pontossággal megmérni. Ezért egy ,,közvetítő'' izzót használhattak a versenyzők: egy közbülső hőmérsékleten, ahol a vizsgált izzó még jól mérhető ellenállású, a szín alapján (vizuálisan) azonos hőmérsékletűre kellett beállítani egy nagyobb ellenállású izzót. Ennek viszont a hideg-ellenállását is meg lehetett mérni, amiből a közbülső hőmérséklet, és így az eredeti izzó eredeti hőmérséklete is számolható volt. Ezután már csak ki kellett választani a megadott Planck-görbékből az izzószál hőmérsékletének megfelelőt, ezzel korrigálhatták a kimért karakterisztikát.   Mágneses korong.   Ez a mérés, az előző ellentéteként, a versenyzőknek szinte teljes szabadságot adott abban, hogy mit és hogyan mérnek. Célszerű volt először csak játszani az eszközzel: különböző szögeknél, különböző magasságokból lecsúsztatni a korongot (hol egyik, hol másik ‐ gyengébben mágneses ‐ oldalán), és közben figyelni a mozgást. Az rögtön látszott, hogy az örvényáramú fékezés miatt a test sebessége előbb-utóbb állandó lett. (Sajnos ezt a magyar versenyzők nyilvánvalónak tekintették, és nem ellenőrizték mérésekkel, hogy különböző esetekben mekkora út megtétele után lesz a sebesség tényleg állandó.) A feladat szerint fel kellett állítani egy elméleti hipotézist arra, hogyan függ a mágneses fékezőerő a korong állandósult sebességétől és a lejtő szögétől. (Természetesen ez a két mennyiség se független egymástól.) Ezután ezt a hipotézist kellett megfelelő mérésekkel igazolni! A mérés elvégzése közben persze érdemes volt néhány ,,apró'' dologra figyelni (például az időmérő szerkezet telepe feszültségének folyamatos ellenőrzése), de a feladat lényege a jó koncepció ‐ hipotézis és mérési eljárás ‐ megtalálása volt. Volt aki tudta vagy ráérzett a fékezőerő és a sebesség közti lineáris kapcsolatra, másvalaki $F\propto v^n$ alakú erőt feltételezett, és $n$ értékét mérte. Olyan (magyar) versenyző is volt, aki $F\propto v^2$ kapcsolatot feltételezett, ezt próbálta igazolni, és amikor az eredményei nem egyeztek a várakozásával, akkor módosította a hipotézisét (és így aranyérmet nyert). Természetesen ennek a feladatnak nem volt könnyű a javítása és a pontozása, hiszen nem lehetett előre látni, milyen utakat választanak a versenyzők. Ezzel együtt sokan örömmel fogadtuk ezt az elmúlt évek olimpiáihoz képest szokatlan, gondolkodtató, ,,nyitott'' feladatot.   Vankó Péter 1A feladatok szövegét októberi számunkban közöltük