Cím:	Az 1998/99. tanévben megrendezett FIZIKA OKTV II. fordulójának feladatmegoldásai
Szerző(k):	Holics László
Füzet:	2000/január, 47 - 55. oldal	PDF  |  MathML
Témakör(ök):	OKTV

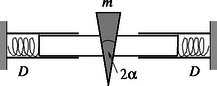
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.     A fizika I. kategória (szakközépiskolások) feladatai     1. ábra     1. feladat. Az ábra szerint egymással szemben rögzítünk két egyforma ,,kilövő szerkezetet", amelyek egy-egy $D=800\text{N/m}$ direkciós erejű rugót tartalmaznak. Ezután közéjük helyezünk egy $m=0\mathrm{,}5\text{kg}$ tömegű, $\alpha ={15}^{\circ }$ félnyílásszögű éket úgy, hogy mindegyik rugó $\Delta l_0=6\text{cm}$-rel összenyomódjon. A hengerek és a rugók tömege valamint minden súrlódás elhanyagolható. a)  Legfeljebb mekkora sebességet érhet el az elengedett ék? b)  Mekkora lehet az ék maximális emelkedése? (Számoljunk $g=10{\text{m/s}}^2$-tel!)  (Jurisits József)    Megoldás. A hengerekre ható erők eredője nulla, ui. a hengerek (az adott közelítésben) tömegtelenek. A hengerre három test hat: a rugó, az ék és a cső fala. A rugóerő a pillanatnyi összenyomódással kifejezve: $F_{\text{r}}=D\Delta l\mathrm{.}$ A cső súrlódásmentes fala csak függőlegesen felfelé ható erőt fejt ki a hengerre. Az egyes hengerek által az ékre kifejtett erő merőleges kell legyen az ék felületére (hiszen nincsen súrlódás). Ez a feltétel akkor teljesül, ha a kérdéses erő függőleges komponensének és a vízszintes komponensének aránya $\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha$. Eszerint az ékre ható teljes függőleges erő: $\begin{array}{c}{\displaystyle \sum F=2D\Delta l\cdot \text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha -mg\mathrm{.}}\end{array}$ Az ék sebessége mindaddig nő, amíg a fenti kifejezés pozitív. A sebesség abban a pillanatban maximális, amikor az erők eredője nulla. Ekkor a rugó pillanatnyi összenyomódásának értéke: $\begin{array}{c}{\displaystyle \Delta l_1=\frac{mg}{2D\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha }=1\mathrm{,}17\text{cm}\mathrm{.}}\end{array}$ A rugó végének elmozdulása ezalatt: $\Delta x=\Delta l_0-\Delta l_1=4\mathrm{,}83\text{cm}$, az ék emelkedése pedig $\Delta y=\text{<span style="font-weight: normal;font-style: normal;">ctg</span>}\alpha \cdot \Delta x=18\text{cm}\mathrm{.}$ Az ék legnagyobb sebességét a munkatétel segítségével kapjuk: $\begin{array}{c}{\displaystyle -mg\Delta y+2\cdot \frac{1}{2}D\left[{\left(\Delta l_0\right)}^2-{\left(\Delta l_1\right)}^2\right]=\frac{1}{2}m{v}_{\text{max}}^2\mathrm{,}}\end{array}$ ahonnan $v_{\text{max}}=1\mathrm{,}68\text{m/s}\mathrm{.}$ Ettől kezdve lassulva emelkedik az ék. A kiindulási helyzettől mért emelkedés magasságát szintén a munkatételből kaphatjuk. A kezdő- és végállapotban az ék sebessége nulla, így $\begin{array}{c}{\displaystyle 2\cdot \frac{1}{2}D{\left(\Delta l_0\right)}^2-mgh=\mathrm{0,}}\end{array}$ ahonnan a maximális emelkedési magasság: $h=57\mathrm{,}6\text{cm}\mathrm{.}$ (Feltettük, hogy a rugók a teljes meglazulásukig működtek. Ez valóban teljesül, hiszen a számított emelkedési $h$ magasság nagyobb, mint $\Delta l_0/\text{<span style="font-weight: normal;font-style: normal;">tg</span>}{15}^{\circ }=0\mathrm{,}224\text{m}$.)   2. feladat. Szobahőmérsékleten egy $V=2$ literes szódásszifonban $V_1=1\mathrm{,}6\text{l}$ szódavíz és felette $V_2=0\mathrm{,}4\text{l}$ térfogatú, $p=240\text{kPa}$ nyomású ${\text{CO}}_2$ gáz van. Maximálisan mennyi szódavíz engedhető ki a szifonból, ha a külső nyomás $p_0=100\text{kPa}$? (Szobahőmérsékleten a víz felett $100\text{kPa}$ $\text{C<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>O</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow></math>}$ gáznyomás esetén $1\text{l}$ vízben annyi $\text{C<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>O</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow></math>}$ gáz oldódik, amelynek térfogata $100\text{kPa}$ nyomásnál $v=0\mathrm{,}8\text{l}$; a víz feletti egyéb $p$ nyomásnál az oldott $\text{C<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>O</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow></math>}$ gáznak a $100\text{kPa}$ nyomásra átszámított térfogata $pv/p_0$. A szifonban levő levegő hatását hanyagoljuk el! A szifon csöve az edény aljáig ér le.)  (Blészer Jenő)    Megoldás. Határozzuk meg először az 1 liter vízben oldott $\text{C<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>O</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow></math>}$ tömeghányadát. $p_0$ gáznyomás esetén az oldott szén-dioxid térfogata $T=300$ K hőmérsékleten (a feladat szövege szerint) $v$ térfogatú, azaz $\begin{array}{c}{\displaystyle m_0=\frac{p_{0}vM}{RT}}\end{array}$ tömegű. ($M=44\text{g}/$mol a szén-dioxid moláris tömege.) $p$ gáznyomás esetén oldott $\text{C<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>O</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow></math>}$ $p_0$ nyomáson, $T$ hőmérsékleten $pv/p_0$ térfogatú, a tömege tehát $\begin{array}{c}{\displaystyle m=\frac{p_0}{RT}\frac{p}{p_0}vM=\frac{pvM}{RT}\mathrm{.}}\end{array}$ Ezekből a $p$ gáznyomás esetén $V^{*}=1$ liter vízben oldott $\text{C<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>O</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow></math>}$ és az őt tartalmazó ($\varrho$ sűrűségű) víz tömeghányada: $\begin{array}{c}{\displaystyle \mu =\frac{m}{m_{víz}}=\frac{m}{V^{*}\varrho }=\frac{pvM}{V^{*}\varrho RT}=\frac{4}{5}\frac{M}{\varrho RT}p\mathrm{.}}\end{array}$ (1) Számítsuk ki a $V_{\text{ö}}$ össztérfogatú szifonban levő $\text{C<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>O</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow></math>}$ össztömegét, ha a gáz $V$ térfogatú és $p$ nyomású: $\begin{array}{c}{\displaystyle m\left(p\mathrm{,}V\right)=m_{\text{gáztérben}}+m_{\text{vízben oldva}}}\end{array}$ azaz $\begin{array}{c}{\displaystyle m\left(p\mathrm{,}V\right)=\frac{MpV}{RT}+\left(V_{\text{ö}}-V\right)\varrho \cdot \mu \mathrm{,}}\end{array}$ ami (1) felhasználásával $\begin{array}{c}{\displaystyle m\left(p\mathrm{,}V\right)=\frac{M}{5RT}p\left(V+4V_{\text{ö}}\right)}\end{array}$ (2) alakra hozható. A gáz kezdeti nyomása $p_{\text{k}}=240$ kPa, a végső nyomás $p_{\text{v}}=100$ kPa, a kezdeti térfogata $V_{\text{k}}=0\mathrm{,}4{\text{dm}}^3\mathrm{,}$ végső térfogata ($V_{\text{v}}$) pedig a feladat tulajdonképpeni kérdése. A folyamat elején, illetve végén az oldott $\text{C<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>O</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow></math>}$ tömeghányada (1) alapján: $\begin{array}{c}{\displaystyle {\mu }_{\text{k}}=\frac{4}{5}\frac{M}{\varrho RT}{p}_{\text{k}}\mathrm{,}\text{illetve}{\mu }_{\text{v}}=\frac{4}{5}\frac{M}{\varrho RT}{p}_{\text{v}}\mathrm{.}}\end{array}$ Az oldott $\text{C<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>O</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow></math>}$ tömegaránya a nyomás csökkenése miatt változik. Közelítsük a folyamat átlagos tömeghányadát számtani középpel${}^{*}$: $\begin{array}{c}{\displaystyle \overline{\mu }=\frac{{\mu }_{\text{k}}+{\mu }_{\text{v}}}{2}=\frac{4}{5}\frac{M}{\varrho RT}\frac{p_{\text{k}}+p_{\text{v}}}{2}\mathrm{.}}\end{array}$ Az eltávozott $\Delta V=V_{\text{v}}-V_{\text{k}}$ térfogatú víz kivisz magával $\left(V_{\text{v}}-V_{\text{k}}\right)\varrho \overline{\mu }$ tömegű $\text{C<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>O</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow></math>}$-t. A szén-dioxid össztömegének állandóságát kifejező egyenlet (tömegmérleg): $\begin{array}{c}{\displaystyle m\left(p_{\text{k}}\mathrm{,}{V}_{\text{k}}\right)=m\left(p_{\text{v}}\mathrm{,}{V}_{\text{v}}\right)+\left(V_{\text{v}}-V_{\text{k}}\right)\varrho \overline{\mu }\mathrm{,}}\end{array}$ ami (2) felhasználásával: $\begin{array}{c}{\displaystyle \frac{M}{5RT}{p}_{\text{k}}\left(V_{\text{k}}+4V_{\text{ö}}\right)=\frac{M}{5RT}{p}_{\text{v}}\left(V_{\text{v}}+4V_{\text{ö}}\right)+\frac{4}{5}\frac{M}{RT}\frac{p_{\text{k}}+p_{\text{k}}}{2}\left(V_{\text{v}}-V_{\text{k}}\right)\mathrm{.}}\end{array}$ Innen $\begin{array}{c}{\displaystyle V_{\text{v}}=\frac{\left(2p_{\text{v}}+3p_{\text{k}}\right)V_{\text{k}}+4\left(p_{\text{k}}-p_{\text{v}}\right)V_{\text{ö}}}{2p_{\text{k}}+3p_{\text{v}}}=1\mathrm{,}91{\text{dm}}^3\mathrm{.}}\end{array}$ A palackban végül 100 kPa nyomású gáz maradt, és $V_{\text{ö}}-V_{\text{v}}=0\mathrm{,}09{\text{dm}}^3$ térfogatú víz nem folyt ki a palackból. A szifonból tehát $1\mathrm{,}51$ liternyi szódavíz (csaknem a teljes kezdeti vízmennyiség) kiengedhető.   3. feladat. Van $N$ darab $U_0$ üresjárási feszültségű, $R$ belső ellenállású egyforma áramforrásunk. Mindegyiket felhasználva telepet készítünk belőlük úgy, hogy először bizonyos számú áramforrást azonos pólussorrendben sorba kapcsolunk egy-egy láncba, majd ezeket a megegyező számú áramforrást tartalmazó láncokat ─ azonos pólusaikat összekötve ─ párhuzamosan kapcsoljuk egymással. A nyert telepre a kivehető teljesítmény szempontjából optimális ellenállású fogyasztót kapcsolunk. a)  Hány telepet kapcsoljunk egy-egy láncba, azaz milyen telepelrendezést készítsünk, hogy a legnagyobb teljesítményt kapjuk a fogyasztón? b)  Mekkora ez a teljesítmény, ha $N=\mathrm{64,}$ $U_0=12\text{V}\mathrm{,}$ $R=2\Omega$?  (Légrádi Imre)    Megoldás. Kapcsoljunk sorba $s$ darab áramforrást egy-egy láncba, így $k=N/s$ darab lánc keletkezik $\left(1\le s\le N\right)$. Egy-egy lánc eredő üresjárási feszültsége $U_1=sU$, eredő belső ellenállása $R_1=sR$. A párhuzamosan kapcsolt láncokból álló telep eredő belső ellenállása $\begin{array}{c}{\displaystyle R_{\text{b}}=\frac{R_1}{k}=\frac{sR}{N/s}=s^2\frac{R}{N}\mathrm{.}}\end{array}$ Ha a kivehető teljesítmény szempontjából optimális ellenállású fogyasztót kapcsolunk a telepre, akkor annak ellenállása a telep belső ellenállásával egyezik meg, vagyis $\begin{array}{c}{\displaystyle R_{\text{f}}=R_{\text{b}}=s^2\frac{R}{N}\mathrm{.}}\end{array}$ A fogyasztón leadott teljesítmény $\begin{array}{c}{\displaystyle P=I^2{R}_{\text{f}}={\left(\frac{sU}{2s^{2}R/N}\right)}^2\frac{s^{2}R}{N}=\frac{U^{2}N}{4R}\mathrm{.}}\end{array}$ Végeredményünkben nem szerepel $s$, ami azt jelenti, hogy az optimális ellenállású fogyasztón minden esetben ugyanakkora teljesítmény jön létre, függetlenül attól, hogy mekkora $s$ értéke, azaz milyen elrendezésű a telepünk. Számadatainkkal $P=1152\text{W}\mathrm{.}$     A fizika II. és III. kategória (valamennyi gimnazista) feladatai     2. 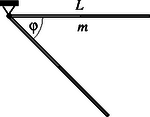ábra     1. feladat. Egy $L$ hosszúságú, $m$ tömegű homogén, vékony rudat egyik végénél fogva csuklósan felfüggesztünk, majd a vízszintesig kitérítjük az ábra szerint. A rudat kezdősebesség nélkül elengedjük. Mekkora és milyen irányú erőt fejt ki a rúd egyik $L/2$ hosszúságú fele a másik $L/2$ hosszúságú felére a $\phi ={60}^{\circ }$-os szögelfordulás pillanatában?  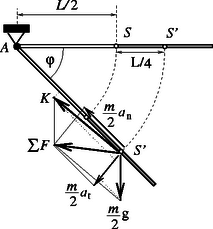(Holics László)    Megoldás. A félrúd által kifejtett (a valójában a két fél találkozási pontjában ható) kényszererőt az alsó félrúd tömegközéppontjának mozgásegyenletéből határozhatjuk meg. A mozgásegyenletet érdemes két komponensre, érintőleges (tangenciális) és sugárirányú (normál) vetületre felírni: $\begin{array}{c}{\displaystyle K_{\text{t}}+\frac{m}{2}g\text{cos}\phi =\frac{m}{2}{a}_{\text{t}}\mathrm{,}}\end{array}$ (1) $\begin{array}{c}{\displaystyle K_{\text{n}}-\frac{m}{2}g\text{sin}\phi =\frac{m}{2}{a}_{\text{n}}\mathrm{.}}\end{array}$ (2)   3. ábra   A $K=\sqrt[]{K_{\text{n}}^2+K_{\text{t}}^2}$ kényszererő meghatározásához a normál és tangenciális gyorsulásokat kell a folyamat dinamikájából meghatározni. Ehhez a pillanatnyi szögsebességre és szöggyorsulásra van szükségünk. A szögsebességet a munkatételből, a szöggyorsulást a forgatónyomaték-tételből kaphatjuk meg. Mivel a félrúd szögadatai azonosak az egész rúdéival, érvényesek a következők: $\begin{array}{c}{\displaystyle mg\frac{L}{2}\text{sin}\phi =\frac{1}{2}\frac{1}{3}m{L}^2{\omega }^2\mathrm{,}}\end{array}$ ahonnan $\begin{array}{c}{\displaystyle L{\omega }^2=3g\text{sin}\phi \mathrm{,}}\end{array}$ (3) valamint $\begin{array}{c}{\displaystyle mg\frac{L}{2}\text{cos}\phi =\frac{1}{3}m{L}^2\beta \mathrm{,}}\end{array}$ innen $\begin{array}{c}{\displaystyle L\beta =\frac{3}{2}g\text{cos}\phi \mathrm{.}}\end{array}$ (4)   4. 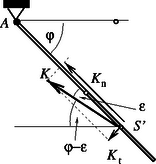ábra   Az (1)‐(4) egyenletekből $a_{\text{t}}=\frac{3}{4}L\beta$ és $a_{\text{n}}=\frac{3}{4}L{\omega }^2$, ezekből a keresett erő két (derékszögű) komponensének nagyságára $\begin{array}{c}{\displaystyle K_{\text{t}}=\frac{1}{16}mg\text{cos}\phi \mathrm{,}\text{valamint}{K}_{\text{n}}=\frac{26}{16}mg\text{sin}\phi }\end{array}$ adódik. A kérdéses erő nagysága: $\begin{array}{c}{\displaystyle K=\frac{1}{16}mg\sqrt[]{\text{cos}{}^2\phi +{26}^2\cdot \text{sin}{}^2\phi }=\frac{\sqrt[]{2029}}{32}mg\approx 1\mathrm{,}4mg\mathrm{.}}\end{array}$ A $K$ erőnek a rúdhoz viszonyított $\epsilon$ irányára fennáll: $\begin{array}{c}{\displaystyle \text{<span style="font-weight: normal;font-style: normal;">tg</span>}\epsilon =\frac{K_{\text{t}}}{K_{\text{n}}}=\frac{1}{26\cdot \sqrt[]{3}}\approx 0\mathrm{,}\mathrm{0222,}}\end{array}$ ahonnan $\epsilon \approx 1\mathrm{,}{27}^{\circ }\mathrm{,}$ a vízszintessel bezárt szög pedig $\alpha =\phi -\epsilon =58\mathrm{,}{73}^{\circ }$.   5. 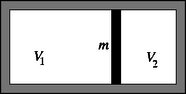ábra     2. feladat. Hőszigetelő falú hengerben $V_1=3$ liter térfogatú, $p_1=4\cdot {10}^5$ Pa nyomású és $T_1=1092$ K hőmérsékletű héliumgázt egy igen jó hőszigetelő, $m=2\text{kg}$ tömegű fal választ el $V_2=2$ liter térfogatú, $p_2=2\mathrm{,}5\cdot {10}^5$ Pa nyomású és $T_2=1365$ K hőmérsékletű héliumgáztól. A válaszfalat elengedjük, ezután a fal súrlódás nélkül mozoghat. Maximálisan mekkora sebességre gyorsul fel a válaszfal?  (Holics László)    Megoldás. A folyamat adiabatikus. A súlyos fal addig gyorsul, míg a két oldalról ható nyomás éppen egyenlővé nem válik. Mivel a dugattyú hőszigetelő, energiát a gáztól hőcserével nem vesz fel. A dugattyú mozgási energiájának megváltozása a rajta végzett munkák összegével egyenlő (munkatétel): $\begin{array}{c}{\displaystyle \frac{1}{2}m{v}^2=W_1+W_2\mathrm{.}}\end{array}$ A két gáz munkája adiabatikus állapotváltozás során belső energiájuk megváltozásának ellentettjével egyenlő, tehát: $\begin{array}{c}{\displaystyle \frac{1}{2}m{v}^2=-\Delta E_1-\Delta E_2\mathrm{.}}\end{array}$ Ismeretes (a hőtan I. főtételéből és a gáztörvényből könnyen megkapható), hogy a gáz belső energiájának megváltozása így is felírható: $\Delta E=\Delta \left(pV\right)/\left(\kappa -1\right)\mathrm{,}$ ahol $\kappa =c_p/c_V$ az ún. fajhőhányados. Ezt felhasználva esetünkben (a második állapothoz tartozó értékeket vesszővel jelölve): $\begin{array}{c}{\displaystyle \frac{1}{2}m{v}^2=\frac{p_1{V}_1+p_2{V}_2}{\kappa -1}-\frac{p{\text{'}}_{1}V{\text{'}}_1+p{\text{'}}_{2}V{\text{'}}_2}{\kappa -1}\mathrm{.}}\end{array}$ Mivel a legnagyobb sebesség elérésekor nem gyorsul a fal, a két gáz nyomása éppen megegyezik, vagyis $p{\text{'}}_1=p{\text{'}}_2=p_{\text{k}}$ közös érték egy pillanatra, és az össztérfogat a dugattyú (fal) elmozdulásával nem változik $\left(V{\text{'}}_1+V{\text{'}}_2=V_1+V_2\right)\mathrm{,}$ ezért egyenletünk így alakul: $\begin{array}{c}{\displaystyle \frac{1}{2}m{v}^2=\frac{p_1{V}_1+p_2{V}_2}{\kappa -1}-\frac{p_{\text{k}}\left(V_1+V_2\right)}{\kappa -1}\mathrm{.}}\end{array}$ A közös $p_{\text{k}}$ nyomást az adiabatikus állapotváltozás egyenletéből $(p^{1/\kappa }\cdot V=\text{állandó}$) határozhatjuk meg: $\begin{array}{c}{\displaystyle p_1^{1/\kappa }{V}_1=p_{\text{k}}^{1/\kappa }V{\text{'}}_1\mathrm{,}}\end{array}$ $\begin{array}{c}{\displaystyle p_2^{1/\kappa }{V}_2=p_{\text{k}}^{1/\kappa }V{\text{'}}_2\mathrm{,}}\end{array}$ Ezeket összeadva (és figyelembe véve, hogy az össztérfogat változatlan) kapjuk, hogy $\begin{array}{c}{\displaystyle p_1^{1/\kappa }{V}_1+p_2^{1/\kappa }{V}_2=p_{\text{k}}^{1/\kappa }\left(V_1+V_2\right)\mathrm{,}}\end{array}$ ahonnan (felhasználva, hogy héliumra $\kappa =\frac{5}{3}$) a közös nyomás $\begin{array}{c}{\displaystyle p_{\text{k}}=\frac{{\left(p_1^{1/\kappa }{V}_1+p_2^{1/\kappa }{V}_2\right)}^{\kappa }}{{\left(V_1+V_2\right)}^{\kappa }}=3\mathrm{,}37\cdot {10}^5\text{Pa}\mathrm{.}}\end{array}$ Ezt az eredményt a fal mozgási energiájának képletébe írva a keresett sebességre végül $v=5\mathrm{,}016\text{m/s}\approx 5\text{m/s}$ adódik.   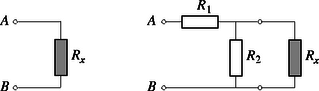3. feladat. A jobb oldali ábrán látható ellenálláslánc a bal oldali ábrán látható ,négypólusból" $n$ számút tartalmaz. $R_1=1\Omega$ és $R_2=6\Omega$. Az ellenálláslánc egy $R_x$ ellenállással van lezárva.   6. ábra   a)  Mekkora legyen az $R_x$ ellenállás értéke, hogy az $A$ és $B$ pontok között mérhető eredő ellenállás értéke független legyen a bekapcsolt négypólusok $n$ számától? b)  Az ellenállásláncot az a) kérdésben meghatározott $R_x$ ellenállással zárjuk le, és az $A$ és $B$ pontok közé $U_{AB}=3\text{V}$ kapocsfeszültségű telepet kapcsolunk. A lánc most $n=21$ négypólust tartalmaz. Határozzuk meg ebben az esetben az $R_x$ ellenállásra eső feszültséget!  (Szegedi Ervin)    Megoldás. a)  Ha a feladat első részében megfogalmazott feltétel teljesíthető, akkor $n=0$ és $n=1$ esetén is teljesül, tehát az $A$ és $B$ pontok között mérhető eredő ellenállás e két esetben egyenlő. Az ábra alapján: $\begin{array}{c}{\displaystyle R_x=R_1+\frac{R_2{R}_x}{R_2+R_x}\mathrm{,}}\end{array}$ (1)   7. ábra   A kérdéses $R_x$-re egy másodfokú egyenletet kapunk: $\begin{array}{c}{\displaystyle R_x^2-R_1{R}_x-R_1{R}_2=\mathrm{0,}}\end{array}$ amelynek megoldása: $R_x=3\Omega$. Meg kell vizsgálnunk, hogy $R_x=3\Omega$ esetén valóban teljesül-e, hogy $R_{AB}$ független a bekapcsolt négypólusok számától! Tekintsük az utolsó négypólust és az azt lezáró $R_x$ ellenállást! Ezek eredője az (1) feltétel alapján $R_x$. Ekkor viszont az utolsó előtti négypólus végeredményben szintén $R_x$ ellenállással van lezárva, ami ismét azt jelenti, hogy az eredő $R_x$. Az eljárást mindaddig folytathatjuk, amíg az első négypólushoz érünk. Ez ismét $R_x$ eredő ellenállású hálózatrésszel van lezárva, tehát az $A$ és $B$ pontok között az eredő ellenállás valóban $R_x$, értéke független a bekapcsolt négypólusok számától. b)  Az utolsó tagon (vagyis az $R_x$ ellenálláson) eső feszültség kiszámításához meg kell határoznunk az $R_x$ ellenálláson átfolyó áram erősségét.   8. 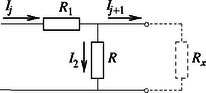ábra   Az első $R_1$ ellenálláson átfolyó áram erőssége $U_{AB}=3\text{V}$ és $R_{AB}=3\Omega$ miatt $I_1=U_{AB}/R_{AB}=1\text{A}\mathrm{.}$ Vizsgáljuk meg ezután egy tetszőleges (mondjuk a $j$-edik) négypólust. Az $R_1$ ellenálláson folyó áram erőssége legyen $I_j$, az $R_x$ ellenálláson folyó áram erőssége pedig $I_{j+1}\mathrm{.}$ Ekkor a csomóponti törvény szerint az $R_2$ ellenálláson $I_j-I_{j+1}$ áram folyik át, és a huroktörvény szerint fenn kell álljon, hogy $\begin{array}{c}{\displaystyle \frac{I_{j+1}}{I_j-I_{j+1}}=\frac{R_2}{R_x}\mathrm{.}}\end{array}$ Innen az áramerősségek arányára $\begin{array}{c}{\displaystyle \frac{I_{j+1}}{I_j}=\frac{R_2}{R_x+R_2}=\frac{2}{3}}\end{array}$ adódik, melyből $I_1$ ismeretében rendre kiszámolhatók a lánc egyes elemein átfolyó áramerősségek: $\begin{array}{c}{\displaystyle I_2=\frac{2}{3}{I}_1\mathrm{,}{I}_3=\frac{2}{3}{I}_2={\left(\frac{2}{3}\right)}^2{I}_1\mathrm{,}\text{...}{I}_n={\left(\frac{2}{3}\right)}^{n-1}{I}_1\mathrm{.}}\end{array}$ Ezzel az $n=21$ tagú láncot lezáró $R_x$ ellenálláson átfolyó áram: $I_{22}=1\text{A}\cdot {\left(\frac{2}{3}\right)}^{21}=0\mathrm{,}2\text{mA}$, az ellenálláson eső feszültség pedig $R_x{I}_{22}=0\mathrm{,}6\text{mV}\mathrm{.}$ Holics László     A fizika I. kategória végeredménye     * 1.Walsch, Thomas William (Szeged, Déri Miksa Ipari Szki., 11. évf.),  tanára: Varjasiné Balla Edit; * 2.Tomon Sándor (Bp., Puskás Tivadar Távközlési Techn., 11. évf.),  tanára: Alapiné Ecseri Éva; * 3.Belicza András (Bp., Puskás Tivadar Távközlési Techn., 11. évf.),  tanára: Szabó Gábor;   4. Belicza Zsolt (Bp., Puskás T. Távk. Techn., 12. évf.), tanára: Szigligeti Márta; 5. Hegedűs Zoltán Csaba (Miskolc, Andrássy Gyula Műsz. Szki. 11. évf.), tanárai: Gonda Gáspár, Dobos Zsolt.     A fizika II. kategória végeredménye     * 1. Felföldi Zsolt (Fazekas Mihály Fővárosi Gyakorló Gimn., 12. évf.),  tanára: Horváth Gábor; * 2. Végh László (Debrecen, Fazekas Mihály Gimn., 12. évf.),  tanárai: Lakatos Tibor, Szegedi Ervin; * 3. Terpai Tamás (Fazekas Mihály Fővárosi Gyakorló Gimn., 12. évf.),  tanára: Horváth Gábor;   4. Tóth Bálint (Fazekas M. Főv. Gyak. Gimn., 12. évf.), tanára: Horváth Gábor; 5. Patakfalvi Zsolt (Fazekas M. Főv. Gyak. Gimn., 12. évf.), tanárai: Horváth Gábor, Dvorák Cecília; 6. Buella Csaba (Tiszaújváros, Eötvös J. Gimn. és Szki., 12. évf.), tanára: Magyari Árpád; 7. Lukács László (Miskolc, Földes F. Gimn., 12. évf.), tanára: Gregáné Ursán Zsuzsanna; 8. Németh András (Fazekas M. Főv. Gyak. Gimn., 12. évf.), tanárai: Horváth Gábor, Dvorák Cecília; 9. Gulyás Nándor (Mezőkovácsháza, Hunyadi J. Gimn., 12. évf.), tanárai: Sallai István, Varga István; 10. Pilászy István (Bp., Piarista Gimn., 12. évf.), tanára: Urbán János.     A fizika III. kategória végeredménye     * 1. Hegedűs Ákos (Pécs, Ciszterci Rend Nagy Lajos Gimnáziuma, 11. évf.),  tanárai: Orovica Márkné, Kotek László; * 2. Máthé András (Budapest, ELTE Apáczai Csere János Gyakorló Gimn., 11. évf.), tanára: Flórik György; * 3. Rácz Balázs (Budapest, Veres Péter Gimn., 12. évf.), tanára: Varga Mária;   4‐5. Gáspár Merse Előd (Fazekas M. Főv. Gyak. Gimn., 11. évf.), tanára: Horváth Gábor; Gönci Balázs (Bp., Móricz Zs. Gimn., 12. évf.), tanára: Horányi Gábor; 6. Buday Tamás (Debrecen, KLTE Gyak. Gimn., 11. évf.), tanárai: Kovács Miklós, Szegedi Ervin; 7. Madarász Tamás (Bp., ELTE Radnóti M. Gyak. Gimn., 12. évf.); tanára: Szalóki Dezső; 8‐9. Ispánovity Péter Dusán (Bp., ELTE Radnóti M. Gyak. Gimn., 12. évf.); tanára: Honyek Gyula; Rozsonday Gerzson (Debrecen, KLTE Gyak. Gimn., 12. évf.), tanárai: Kirsch Éva, Szegedi Ervin; 10‐11. Kajtár Márton (Fazekas M. Főv. Gyak. Gimn., 11. évf.), tanára: Horváth Gábor; Madarász Ádám (Bp., ELTE Radnóti M. Gyak. Gimn., 11. évf.); tanára: Kiss László. ${}^{*}$Felsőbb matematikai módszerekkel a folyamat részletesebben is elemezhető, s ennek eredménye azt mutatja, hogy az alkalmazott közelítés jogos.