Cím:	Az 1999/2000. tanévben megrendezett fizika OKTV II. fordulójának feladatmegoldásai
Szerző(k):	Holics László
Füzet:	2001/január, 44 - 54. oldal	PDF  |  MathML
Témakör(ök):	OKTV

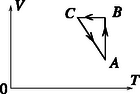
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   A fizika I. kategória (szakközépiskolások) feladatai       1. feladat. Ideális gázzal végezzük az 1. ábra szerinti $ABCA$ körfolyamatot, amelynek grafikonja a $\left(V;T\right)$ térfogat ‐ hőmérséklet síkon derékszögű háromszög, a $V$ és $T$ tengelyekkel párhuzamos befogókkal. A gáz az $A$ ponttal jellemzett állapotában $373\text{K}$ hőmérsékletű, térfogata $5{\text{dm}}^3;$ a $C$ ponttal jellemzett állapotában $273\text{K}$ hőmérsékletű és térfogata $12{\text{dm}}^3$. Határozzuk meg, hogy a körfolyamat $C\to A$ szakaszában mely térfogatnál lesz a gáz nyomása éppen akkora, mint a $B$ ponttal jellemzett állapotában volt!  (Légrádi Imre)    Megoldás. Gay-Lussac I. törvénye szerint a $B$-vel jelzett állapottal azonos nyomású állapotokra fennáll $\begin{array}{c}{\displaystyle T=\frac{T_B}{V_B}V\mathrm{.}}\end{array}$ (1) A keresett állapotot jellemző pont rajta van az $AC$ egyenesen, vagyis kielégíti a $\begin{array}{c}{\displaystyle V-V_C=\frac{V_A-V_B}{T_A-T_B}\cdot \left(T-T_C\right)}\end{array}$ (2) egyenletet. 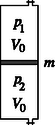Az (1) és (2) egyenletrendszert $V$-re megoldva a keresett térfogatot kapjuk: $\begin{array}{c}{\displaystyle V=V_C\frac{V_A{T}_C-V_C{T}_A}{V_A{T}_A-2V_C{T}_A+V_C{T}_C}\approx 9\mathrm{,}8{\text{dm}}^3\mathrm{.}}\end{array}$     2. feladat. Egy hőszigetelő falú, elhanyagolható hőkapacitású hengerben $A=100{\text{cm}}^2$ keresztmetszetű, $m=0\mathrm{,}5\text{kg}$ tömegű, $c=210\text{J}/\left({\text{kg}}^{\circ }\text{C}\right)$ fajhőjű anyagból készült dugattyú mozoghat függőleges irányban súrlódásmentesen. A $t_0={100}^{\circ }\text{C}$ hőmérsékletű, súlyos dugattyú fölé $n_1=0\mathrm{,}05$ mólnyi $t_1=-{90}^{\circ }\text{C}$-os nemesgázt, a dugattyú alá pedig $n_2=0\mathrm{,}03$ mólnyi $t_2={46}^{\circ }\text{C}$-os levegőt juttatunk. Ekkor a két rész térfogata éppen megegyezik. $a)$ Mennyi lesz a dugattyú végső hőmérséklete? $b)$ Mennyit mozdul el a dugattyú?  (Jurisits József)    Megoldás. $a)$ A kezdeti nyomások és a térfogat kiszámíthatók az állapotegyenletek és a nyomások közötti kapcsolat felhasználásával: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle p_1{V}_0}& {\displaystyle =n_{1}R{T}_1\mathrm{,}}\hfill & \hfill {\displaystyle \left(3\right)}\\ \hfill {\displaystyle p_2{V}_0}& {\displaystyle =n_{2}R{T}_2\mathrm{,}}\hfill \\ \hfill {\displaystyle p_2}& {\displaystyle =p_1+\frac{mg}{A}\mathrm{.}}\hfill \end{array}}}\end{array}$ Ezekből a két rész nyomása meghatározható: $\begin{array}{c}{\displaystyle p_1=\frac{mg}{A}\cdot \frac{n_1{T}_1}{n_2{T}_2-n_1{T}_1}=10\mathrm{,}69\text{kPa}\mathrm{,}}\end{array}$ az alul levő gáz nyomása pedig: $\begin{array}{c}{\displaystyle p_2=p_1+\frac{mg}{A}=11\mathrm{,}18\text{kPa}\mathrm{.}}\end{array}$ A két gázmennyiség azonos kezdeti térfogata a (3) egyenletből: $\begin{array}{c}{\displaystyle V_0=\frac{n_{1}R{T}_1}{p_1}=\frac{A}{mg}R\left(n_2{T}_2-n_1{T}_1\right)=7\mathrm{,}12{\text{dm}}^3\mathrm{.}}\end{array}$ A végső állapot $T$ hőmérsékletének és a dugattyú (lefelé történő) $x$ elmozdulásának kiszámításához felhasználhatjuk az állapotegyenleteket és az energia megmaradásának törvényét. Az állapotegyenlet a felső és az alsó gáz kezdeti és végállapota között: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle \frac{p_1{V}_0}{T_1}}& {\displaystyle =\frac{p\left(V_0+xA\right)}{T}\mathrm{,}}\hfill & \hfill {\displaystyle \left(4\right)}\\ \hfill {\displaystyle \frac{p_2{V}_0}{T_2}}& {\displaystyle =\frac{\left(p+\frac{mg}{A}\right)\left(V_0-xA\right)}{T}\mathrm{.}}\hfill & \hfill {\displaystyle \left(5\right)}\end{array}}}\end{array}$ Az energia megmaradásának törvénye a teljes folyamatra a hőszigetelő edényben: $\begin{array}{c}{\displaystyle \frac{f_1}{2}{n}_{1}R\left(T-T_1\right)+\frac{f_2}{2}{n}_{2}R\left(T-T_2\right)+cm\left(T-T_0\right)-mgx=0.}\end{array}$ (6) A fenti három egyenlet egyértelműen meghatározza a $T$, $p$ és $x$ ismeretleneket. Az egyenletrendszer megoldása akkor egyszerű, ha észrevesszük, hogy a dugattyú súlyából származó nyomás nagyságrendekkel kisebb, mint a gázok nyomása, így az elhanyagolgató. (Míg a felső térrészben ható nyomás $10\mathrm{,}7$ kPa, az alsóban $11\mathrm{,}2$ kPa, addig a dugattyú nyomása $0\mathrm{,}5$ kPa, ami a gáznyomások $5\%$-át sem éri el!) Ebben a közelítésben (5) így írható: $\begin{array}{c}{\displaystyle \frac{p_2{V}_0}{T_2}=\frac{p\left(V_0-xA\right)}{T}\mathrm{.}}\end{array}$ (5') (4)-t $\left(5\text{'}\right)$-vel osztva mind $p$, mind $T$ kiesik. (Ez nem azt jelenti, hogy az eredmény független a hőmérsékletváltozástól és a nyomásváltozástól, mert a pontos összefüggésben még $mg/A$ is szerepel!) $\begin{array}{c}{\displaystyle \frac{p_1{T}_2}{p_2{T}_1}=\frac{V_0+xA}{V_0-xA}\mathrm{,}}\end{array}$ ahonnan a dugattyú elmozdulása: $\begin{array}{c}{\displaystyle x=\frac{p_1{T}_2-p_2{T}_1}{p_1{T}_2+p_2{T}_1}\frac{V_0}{A}\approx 18\text{cm}\mathrm{.}}\end{array}$ A (6) energiaegyenletből (a $-mgx$ tag elhanyagolásával) kifejezhetjük a kialakuló közös egyensúlyi hőmérsékletet: $\begin{array}{c}{\displaystyle T=\frac{\left(f_1{n}_1{T}_1+f_2{n}_2{T}_2\right)R+\left(2c{T}_0-2gx\right)m}{\left(f_1{n}_1+f_2{n}_2\right)R+2mc}\approx \frac{\left(f_1{n}_1{T}_1+f_2{n}_2{T}_2\right)R+2c{T}_{0}m}{\left(f_1{n}_1+f_2{n}_2\right)R+2mc}=371\mathrm{,}6\text{K}\mathrm{.}}\end{array}$ Megjegyzés. Amennyiben a (6) egyenletből indulunk ki (ott viszonylag kisebb elhanyagolás az $x$-et tartalmazó tag elhagyása), a kiszámított $T$ hőmérsékletet a (4) és (5) állapotegyenletekbe írva a dugattyú elmozdulására egy másodfokú egyenletet kapunk, melynek megoldása: $18\mathrm{,}7$cm. Ez az előzőnél pontosabb érték, de mind a két számítás elfogadható.   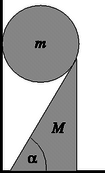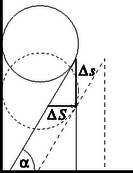3. feladat. Egy függőleges fal és egy vízszintes síkon álló $\alpha$ hajlásszögű, $M$ tömegű derékszögű ék közé $m$ tömegű golyót helyezünk úgy, hogy az ék lapja a legfelső pontjában éppen érintse a golyót a 3. ábra szerint. Az ék és a golyó is súrlódásmentesen csúszhat. $a)$ Hogyan kell megválasztanunk az $M/m$ tömegarányt és az $\alpha$ hajlásszöget, hogy a golyó elengedése után a lejtő ne billenjen meg? $b)$ Mekkora sebességet ér el a golyó, miközben az éknek $l=20\text{cm}$ hosszú szakaszán csúszik végig, ha $\alpha ={60}^{\circ }$ és $M/m=12$?  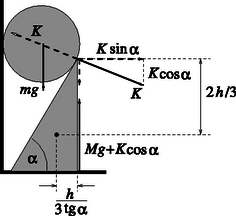(Jurisits József)    Megoldás. Írjuk fel a golyó és a lejtő mozgásegyenletét, valamint a gyorsulások kapcsolatát. Jelöljük a golyó adatait kis, az ék adatait nagy betűkkel! A 4. ábra alapján: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle mg-K\text{cos}\alpha }& {\displaystyle =ma\mathrm{,}}\hfill & \hfill {\displaystyle \left(7\right)}\\ \hfill {\displaystyle K\text{sin}\alpha }& {\displaystyle =MA\mathrm{,}}\hfill & \hfill {\displaystyle \left(8\right)}\\ \hfill {\displaystyle a}& {\displaystyle =A\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha \mathrm{.}}\hfill & \hfill {\displaystyle \left(9\right)}\end{array}}}\end{array}$ Az utóbbi összefüggés abból a kényszerfeltételből adódik, hogy a golyó mindvégig érinti az ék lapját. A golyó és az ék útja $t$ idő alatt: $\begin{array}{c}{\displaystyle \Delta s=\frac{a}{2}{t}^2\mathrm{,}\text{illetve}\Delta S=\frac{A}{2}{t}^2\mathrm{,}}\end{array}$ ugyanis az erők és így a gyorsulások is állandók. Az 5. ábráról leolvasható, hogy $\begin{array}{c}{\displaystyle \Delta s=\Delta S\cdot \text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha \mathrm{,}}\end{array}$ vagyis $\begin{array}{c}{\displaystyle \frac{a}{2}{t}^2=\frac{A}{2}{t}^2\cdot \text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha \mathrm{,}}\end{array}$ ahonnan $t^2/2$-vel osztva (9) adódik. A (7)‐(9) egyenletrendszert megoldva $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle a}& {\displaystyle =\frac{\text{<span style="font-weight: normal;font-style: normal;">tg</span>}{}^2\alpha }{\left(M/m\right)+\text{<span style="font-weight: normal;font-style: normal;">tg</span>}{}^2\alpha }g\mathrm{,}}\hfill & \hfill {\displaystyle \left(10\right)}\\ \hfill {\displaystyle K}& {\displaystyle =\frac{1}{\left(M/m\right)+\text{<span style="font-weight: normal;font-style: normal;">tg</span>}{}^2\alpha }\cdot \frac{Mg}{\text{cos}\alpha }\mathrm{,}}\hfill & \hfill {\displaystyle \left(11\right)}\\ \hfill {\displaystyle A}& {\displaystyle =\frac{\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha }{\left(M/m\right)+\text{<span style="font-weight: normal;font-style: normal;">tg</span>}{}^2\alpha }g\mathrm{.}}\hfill & \hfill {\displaystyle \left(12\right)}\end{array}}}\end{array}$ Annak a feltétele, hogy az ék ne billenjen meg az ék tömegközéppontjára felírható forgatónyomaték-tétellel kifejezve a 4. ábra alapján: $\begin{array}{c}{\displaystyle \frac{2}{3}Kh\text{sin}\alpha +K\text{cos}\alpha \frac{h}{3\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha }\le \left(Mg+K\text{cos}\alpha \right)\frac{h}{3\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha }\mathrm{.}}\end{array}$ (13) (Felhasználtuk, hogy határesetben a talaj által az ékre kifejtett kényszererő hatásvonala az ék jobb szélére tolódik el.) A (13) egyenlőtlenségből (11) felhasználásával a tömegarányra a $\begin{array}{c}{\displaystyle \frac{M}{m}\ge \text{<span style="font-weight: normal;font-style: normal;">tg</span>}{}^2\alpha }\end{array}$ megszorítást, a golyó gyorsulására pedig az $\begin{array}{c}{\displaystyle a\le \frac{g}{2}}\end{array}$ felső korlátot kapjuk. $b)$ Ha $\alpha ={60}^{\circ }$, akkor $M/m\ge \text{<span style="font-weight: normal;font-style: normal;">tg</span>}{}^2{60}^{\circ }=3$ szükséges, tehát a megadott $M/m=12$ esetén nem billen az ék. A mechanikai energia megmaradásának tétele szerint: $\begin{array}{c}{\displaystyle mgl\text{sin}\alpha =\frac{1}{2}m{v}^2+\frac{1}{2}M{V}^2\mathrm{.}}\end{array}$ (14) A sebességek kapcsolata (hasonlóan a gyorsulások kényszerkapcsolatához): $V=v/\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha$, melyet (14)-be helyettesítve a golyó sebességére ($l$ lejtőmenti szakasz befutása után) a következő adódik: $\begin{array}{c}{\displaystyle v=\sqrt[]{\frac{2gl\text{sin}\alpha }{1+\frac{M}{m\text{<span style="font-weight: normal;font-style: normal;">tg</span>}{}^2\alpha }}}\approx 0\mathrm{,}82\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>m</mi></mrow><mrow><mi>s</mi></mrow></mfrac></mrow></math>}\mathrm{.}}\end{array}$       A fizika II. és III. 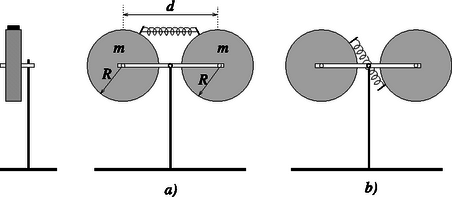kategória (valamennyi gimnazista) feladatai       1. feladat. Elhanyagolható tömegű, közepén tengelyezett, könnyen forgó rúd két végén szimmetrikusan egy-egy $R=10\text{cm}$ sugarú, $m=4\text{kg}$ tömegű homogén tömör korong van vízszintes tengelyhez erősítve a 6. ábra szerint. A korongok tengelyei egymástól $d=25\text{cm}$-re vannak. A korongok palástján elhanyagolható tömegű pöckök közé $D=1800\text{N/m}$ direkciós erejű rugó van elhelyezve $\Delta l=5\text{cm}$-rel összenyomott állapotban. Mekkora lesz a korongok szögsebessége, miután a rugót feszesen tartó fonalat elégetjük, ha a pöckök eredetileg a 6.a, illetve a 6.b ábra szerint helyezkednek el? (A rugók teljes megnyúlásig érintkeznek a pöckökkel, s ezután leesnek.)  (Holics László)    Megoldás. $a)$ eset. Mivel a külső forgatónyomatékok összege nulla, a perdület megmarad. A rugó kitágulása után a két egyforma korong egymással ellentétes irányban, azonos nagyságú szögsebességgel kezd forogni. A rugó teljes energiája a két korong forgási energiájába alakul át: $\begin{array}{c}{\displaystyle \frac{1}{2}D{\left(\Delta l\right)}^2=2\cdot \frac{1}{2}\Theta {\omega }_a^2\mathrm{.}}\end{array}$ Felhasználva, hogy a korongok tehetetlenségi nyomatéka $\Theta =\frac{1}{2}m{R}^2$, a keresett szögsebesség: $\begin{array}{c}{\displaystyle {\omega }_a=\frac{\Delta l}{R}\sqrt[]{\frac{D}{m}}=10\mathrm{,}6\frac{1}{\text{s}}\mathrm{.}}\end{array}$ $b)$ eset. A két korong most azonos irányban kezd el forogni, de mivel a külső forgatónyomatékok összege most is nulla, a rendszer teljes perdületének meg kell maradnia. Ez csak úgy lehetséges, hogy a két korongot tartó (elhanyagolható tömegű) rúd elfordul a korongokkal, azok szögsebességével ellentétes irányban. Így a korongok ‐ azonos irányú ‐ sajátperdülete, és a rendszer forgása miatt keletkező ‐ a sajátperdülettel ellentétes irányú ‐ pályaperdülete egyenlő abszolút értékű. Az energia megmaradása: $\begin{array}{c}{\displaystyle \frac{1}{2}D{\left(\Delta l\right)}^2=2\cdot \frac{1}{2}\Theta {\omega }_b^2+2\cdot \frac{1}{2}m{v}^2\mathrm{,}}\end{array}$ (15) a perdület megmaradása: $\begin{array}{c}{\displaystyle 2\cdot \Theta {\omega }_b-2\cdot mv\frac{d}{2}=\mathrm{0,}}\end{array}$ (16) ahol $v$ a korongok tömegközéppontjának sebessége. 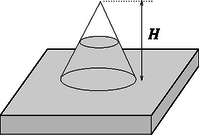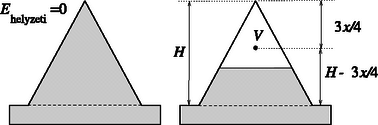(16)-ból $v$-t kifejezve és (15) egyenletbe helyettesítve megkapjuk a korongok szögsebességét: $\begin{array}{c}{\displaystyle {\omega }_b=\frac{\Delta l}{R}\frac{d}{\sqrt[]{d^2+2R^2}}\sqrt[]{\frac{D}{m}}=9\mathrm{,}23\frac{1}{\text{s}}\mathrm{.}}\end{array}$ (17)   2. feladat. Egyenes körkúp alakú, vékonyfalú üvegedény alsó, nyitott vége higannyal telt kádba merül. Az üvegkúp csúcsa $H=76\text{cm}$ magasan van a kádbeli higanyszint felett. Az üvegedényt részben higany tölti ki. A higany feletti zárt térrészben $n=0\mathrm{,}01\text{mol}$ levegő van. A külső légköri nyomás $H=76\text{cm}$ magasságú higanyoszlop hidrosztatikai nyomásával egyenlő. Mennyi hőt vesz fel az elzárt levegő, ha hőmérséklete lassan $\Delta T=10{}^{\circ }\text{C}$-kal emelkedik? (A kádbeli higanyszint változása elhanyagolható, a kúpbeli higanyszint nem süllyed a kádbeli higanyszint alá.)  (Szegedi Ervin)    Megoldás. Határozzuk meg, hogyan függ a kúpba bezárt gáz nyomása a gázkúp magasságától! Mivel a külső légnyomás $H$ magasságú higany hidrosztatikai nyomásával tart egyensúlyt, a kúpba zárt higany magassága pedig $H-x$ (8. ábra), a bezárt levegő nyomása a hiányzó $x$ magasságú higany nyomását kell, hogy pótolja, vagyis $p=\varrho gx$, azaz a bezárt gáz nyomása egyenlő az általa alkotott kúp magasságával azonos magasságú higany hidrosztatikai nyomásával. Tudjuk viszont, hogy a külső nyomás $\begin{array}{c}{\displaystyle p_{\text{k}}=\varrho gH\mathrm{,}}\end{array}$ (18) a kádbeli higany felületénél pedig a nyomás mindenhol (tehát a kúpon kívül és azon belül is) ugyanakkora: $\begin{array}{c}{\displaystyle p_{\text{k}}=p+\varrho g\left(H-x\right)\mathrm{.}}\end{array}$ (19) (18) és (19) alapján valóban igaz $\begin{array}{c}{\displaystyle p=\varrho gx\mathrm{.}}\end{array}$ (20) Számítsuk ki (a hőtan a I. főtételének alkalmazásával) a gáz hőfelvételét: $\begin{array}{c}{\displaystyle Q=\Delta E+W_{\text{gáz}}\mathrm{.}}\end{array}$ Az energiaváltozást a hőmérsékletváltozás egyértelműen megadja. Az ekvipartíció tétele alapján: $\begin{array}{c}{\displaystyle \Delta E=\frac{f}{2}Nk\Delta T=\frac{f}{2}n{N}_{A}k\Delta T=\frac{f}{2}nR\Delta T\mathrm{.}}\end{array}$ A gáz által felvett hő tehát (mivel levegőre $f=5$): $\begin{array}{c}{\displaystyle Q=\frac{5}{2}nR\Delta T+W_{\text{gáz}}\mathrm{.}}\end{array}$ (21) Határozzuk meg a gáz által végzett munkát! (Ez okozza az igazi nehézséget a megoldás során.) Mivel a gáz nyomása a térfogat függvényében nem lineárisan változik, ezért az elemi munkák összegezése csak integrálással tehető meg. Keressünk más megoldást! Alkalmazzuk a munkatételt a kádbeli és kúpbeli higany rendszerére a kezdeti és végállapot között! A higanyon a kitáguló kúpbeli levegő, a nehézségi erő és a külső levegő végez munkát. (A kádbeli higany ugyan elhanyagolható mértékben emelkedik, de nagy felületen, ezért az általa kiszorított levegő térfogata nem elhanyagolható!) A bezárt gáz és a nehézségi erő munkája pozitív, a külső levegőé pedig negatív. Mivel a higany mozgási energiája nem változik, ezért az összes munkák összege zérus: $\begin{array}{c}{\displaystyle W_{\text{gáz}}+W_{\text{nehézségi}}+W_{\text{külső}}=0.}\end{array}$ Tekintve, hogy a nehézségi erő munkája a helyzeti energia megváltozásának ellentettjével egyenlő, a bezárt gáz munkájára a következő összefüggést kapjuk: $\begin{array}{c}{\displaystyle W_{\text{gáz}}=\Delta E_{\text{helyzeti}}-W_{\text{külső}}=0.}\end{array}$ A külső, állandó nyomású levegő munkavégzése könnyen kapható, hiszen térfogatváltozása az elzárt levegő térfogatváltozásának ellentettje: $\begin{array}{c}{\displaystyle W_{\text{külső}}=p_{\text{k}}\Delta V=-p_{\text{k}}\left(V_2-V_1\right)\mathrm{.}}\end{array}$ Az elzárt gáz munkája tehát ezzel így írható: $\begin{array}{c}{\displaystyle W_{\text{gáz}}=\Delta E_{\text{helyzeti}}-p_{\text{k}}\left(V_2-V_1\right)\mathrm{.}}\end{array}$ (22) 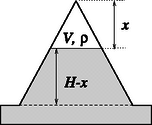Hátra van még a higany helyzeti (,,magassági'') energiája megváltozásának meghatározása. E célból első lépésként írjuk fel ezt az energiát általános helyzetben! Válasszuk a helyzeti energia nullszintjét úgy, hogy akkor legyen nulla a helyzeti energia, amikor a higany teljesen kitölti az üvegkúpot! A vizsgált helyzetben (9. ábra) a higany helyzeti energiája a nulla energiánál $\begin{array}{c}{\displaystyle \varrho Vg\left(H-\frac{3}{4}x\right)}\end{array}$ értékkel kevesebb, hiszen a $V$ térfogatú részt kezdetben kitöltő higany tömegközéppontja $\Delta h=\left(H-\frac{3}{4}x\right)$ értékkel mélyebbre került (mintha a kúp csúcsában levő higanymennyiség került volna ki az üvegből és terült volna szét a nagy felületű kádban), a többi higany energiája nem változott. (Felhasználtuk a Függvénytáblázatból is kiolvasható ismeretet, hogy a homogén anyaggal kitöltött $x$ magasságú egyenes körkúp tömegközéppontja az alaplap felett $x/4$ magasságban van. Az $x$ magasságú higanykúp helyzeti energiája tehát: $\begin{array}{c}{\displaystyle E_{\text{helyzeti}}=-\varrho Vg\left(H-\frac{3}{4}x\right)\mathrm{,}}\end{array}$ vagy (18) és (19) szerint: $\begin{array}{c}{\displaystyle E_{\text{helyzeti}}=\frac{3}{4}\varrho gxV-\varrho VgH=\frac{3}{4}pV-p_{\text{k}}V\mathrm{.}}\end{array}$ (23) A vizsgált folyamatban a higany helyzeti energiájának megváltozása tehát (22) szerint: $\begin{array}{c}{\displaystyle E_{\text{helyzeti}}=\frac{3}{4}\left(p_2{V}_2-p_1{V}_1\right)-p_{\text{k}}\left(V_2-V_1\right)\mathrm{.}}\end{array}$ (24) A gáz munkája tehát (22) alapján, (24) felhasználásával: $\begin{array}{c}{\displaystyle W_{\text{gáz}}=\Delta E_{\text{helyzeti}}-p_{\text{k}}\left(V_2-V_1\right)=\frac{3}{4}\left(p_2{V}_2-p_1{V}_1\right)\mathrm{,}}\end{array}$ ami a $pV=nRT$ állapotegyenlet szerint $\begin{array}{c}{\displaystyle W_{\text{gáz}}=\frac{3}{4}nR\Delta T}\end{array}$ (25) alakba írható. A folyamatban felvett hő (21) és (25) alapján tehát: $\begin{array}{c}{\displaystyle Q=\left(\frac{5}{2}+\frac{3}{4}\right)nR\Delta T=\frac{13}{4}nR\Delta T=2\mathrm{,}70\text{J}\mathrm{.}}\end{array}$ Megjegyzés. A gáz munkája integrálással is kiszámítható. Határozzuk meg a gáz állapotváltozásának $p\left(V\right)$ függvényét! A gázkúp térfogata $V=\pi r^{2}x/\mathrm{3,}$ ahol $r$ a kúp alapkörének sugara, amely a kúp fél nyílásszögével és magasságával is kifejezhető: $r=x\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha \mathrm{.}$ Ezek szerint $\begin{array}{c}{\displaystyle V=\frac{\pi }{3}{x}^3\text{<span style="font-weight: normal;font-style: normal;">tg</span>}{}^3\alpha \mathrm{,}}\end{array}$ ahonnan a gázkúp magassága térfogatával kifejezve: $\begin{array}{c}{\displaystyle x=\sqrt[3]{\frac{3}{\pi \text{<span style="font-weight: normal;font-style: normal;">tg</span>}{}^2\alpha }}\cdot V^{\frac{1}{3}}\mathrm{.}}\end{array}$ (26) (20) és (26) alapján: $\begin{array}{c}{\displaystyle p=\varrho g\sqrt[3]{\frac{3}{\pi \text{<span style="font-weight: normal;font-style: normal;">tg</span>}{}^2\alpha }}\cdot V^{\frac{1}{3}}\mathrm{,}}\end{array}$ azaz $\begin{array}{c}{\displaystyle p=\beta V^{\frac{1}{3}}\mathrm{,}}\end{array}$ (27) ahol $\begin{array}{c}{\displaystyle \beta =\varrho g\sqrt[3]{\frac{3}{\pi \text{<span style="font-weight: normal;font-style: normal;">tg</span>}{}^2\alpha }}\mathrm{.}}\end{array}$ A gáz nyomása tehát arányos térfogatának köbgyökével. A gáz munkája a kezdeti- és végállapot között az elemi munkák összegezésével kapható: $\begin{array}{c}{\displaystyle W_{\text{gáz}}=\underset{V_1}{\overset{V_2}{\int }}pdV=\beta \underset{V_1}{\overset{V_2}{\int }}{V}^{\frac{1}{3}}dV=\frac{3}{4}\beta \left(V_2^{\frac{4}{3}}-V_1^{\frac{4}{3}}\right)\mathrm{.}}\end{array}$ Az eredményt alkalmasan tagolva és (27) alapján alakítva: $\begin{array}{c}{\displaystyle W_{\text{gáz}}=\frac{3}{4}\left(\beta V_2^{\frac{1}{3}}{V}_2-\beta V_1^{\frac{1}{3}}{V}_1\right)=\frac{3}{4}\left(p_2{V}_2-p_1{V}_1\right)=\frac{3}{4}nR\Delta T\mathrm{,}}\end{array}$ ami megegyezik az előző gondolatmenetben adódó alakkal.   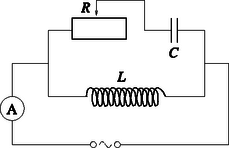3. feladat. A 10. ábra szerinti áramkörben a tekercs önindukciós együtthatója $L=10\text{mH}$, a kondenzátor kapacitása $C=0\mathrm{,}2\text{mF}$. Az áramkörre váltakozó feszültséget kapcsolunk. Mekkora a váltakozó feszültség frekvenciája, ha azt tapasztaljuk, hogy a főágba kapcsolt ideális áramerősségmérő műszer által mutatott érték független az ohmos ellenállás nagyságától?  (Szegedi Ervin)    Megoldás. Ha a főág áramerőssége független az ohmos ellenállás $R$ nagyságától, akkor speciálisan a nagyon kicsiny és a nagyon nagy ellenállásoknál ugyanakkora értéket kell mutasson az árammérő műszer. Rövidzárnál ($R=0$) a tekercsre és a kondenzátorra egyaránt $U$ (effektív) feszültség jut, a rajtuk átfolyó áram $\begin{array}{c}{\displaystyle I_{\text{tekercs}}=U\cdot \frac{1}{L\omega }\mathrm{,}\text{illetve}{I}_{\text{kondenzátor}}=U\cdot \omega C\mathrm{.}}\end{array}$ Ez a két áram ellentétes fázisú, a főág effektív áramerőssége tehát $\begin{array}{c}{\displaystyle I_1=U\cdot \left|\omega C-\frac{1}{L\omega }\right|\mathrm{.}}\end{array}$ Ha viszont az ohmos ellenállást nagyon nagy értékre állítjuk be, netán megszakítjuk az áramkört ($R\to \infty$), áram csak a tekercsen folyhat, így a műszer által mutatott érték $\begin{array}{c}{\displaystyle I_2=U\cdot \frac{1}{L\omega }\mathrm{.}}\end{array}$ A feladatban megfogalmazott feltétel szerint $I_1=I_2$, ami akkor teljesül, ha $\begin{array}{c}{\displaystyle \omega =\sqrt[]{\frac{2}{LC}}=1000\text{Hz}\mathrm{,}}\end{array}$ a frekvencia tehát $f=\omega /\left(2\pi \right)=159\mathrm{,}2\text{Hz}$.   Megjegyzés. 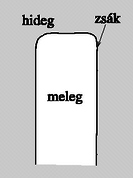Forgóvektorokkal vagy komplex impedanciákkal számolva belátható, hogy a fenti frekvencia-feltétel teljesülése esetén az impedancia a teljes $R$ tartományban független lesz az ohmos ellenállástól, nagysága: $Z=L\omega \mathrm{.}$   4. feladat. Tapasztalatból tudjuk, hogy ha egy nyitott szájával lefelé tartott szemeteszsákot megtöltünk meleg levegővel, akkor a zsák ‐ a hőlégballonhoz hasonlóan ‐ felemelkedik. Hol a hiba a következő gondolatmenetben: ,,A zsák szája nyitott, ezért a külső és a belső levegő nyomása egyenlő. A zsák (felül levő) zárt alját ezért a belső levegő ugyanakkora erővel nyomja felfelé, mint a külső levegő lefelé. Mivel ezek az erők kiegyenlítik egymást, azért a zsák anyagára ható nehézségi erő miatt a zsák leesik.''   Megoldás. A zsák szájánál valóban azonos a meleg és a hideg levegő nyomása $\left(p_0\right)$. A $h$ magasságú zsák zárt alja $h$-val magasabban van a zsák szájánál, ezért a levegő nyomása kívül is, belül is kisebb $p_0$-nál. Jelölje ezt a nyomást a külső, hidegebb levegőben $p_{\text{H}}$, belül pedig $p_{\text{M}}$. A légnyomás változása a magassággal kis szintkülönbségek esetén közelítőleg a $\Delta p=-\varrho gh$ összefüggés alapján számolható. Esetünkben a külső és belső levegő sűrűsége számottevően eltér (közel azonos a nyomásuk, de hőmérsékletük jelentősen különbözik), ${\varrho }_{\text{H}}>{\varrho }_{\text{M}}$. Ez azt eredményezi, hogy a belső meleg levegőben ugyanazon $h$ távolságon kevesebbet csökken a nyomás, mint a külső, hideg levegőben, így a zsák felül levő zárt alján belül nagyobb a nyomás mint kívül: $p_{\text{M}}>p_{\text{H}}$, a nyomáskülönbség pedig felfelé mutató emelőerőt eredményez. Ha ez meghaladja a zsák anyagára ható nehézségi erőt, akkor a zsák felemelkedik.       A fizika I. kategória végeredménye     1. Tomon Sándor (Budapest, Puskás Tivadar Távközlési Technikum, 12. évf.),  tanára: Beregszászi Zoltán; 2. Gyurcsek Tamás (Szolnok, Pálfy J. Műszerip. és Vegyip. Szakközépisk., 12. évf.), tanára: Báthori Attila; 3. Laczkó Péter (Budapest, Egressy Gábor Kéttannyelvű Műsz. Szakközépisk., 12. évf.),  tanára: Berta Magdolna;   4. Oláh Gusztáv (Debrecen, Mechwart A. Gépip. és Informatikai Középisk., 12. évf.), tanárai: Gál Annamária, Szegedi Ervin; 5. Perge István (Eger, Neumann János Közgazd. Szki. és Gimn., 11. évf.), tanára: Fátrai Éva; 6. Hoffer János Pál (Kecskemét, Kandó K. Műszaki Szki., 11. évf.), tanára: Jusztin Zsuzsanna; 7. Magyar Máté (Vác, Boronkay Gy. Műszaki Középisk. és Gimn., 12. évf.), tanára: Csomó József; 8. Tóth Árpád (Jászberény, Liska J. Erősáramú Szki. és Gimn., 12. évf.), tanára: Máthéné Barabássy Judit.       A fizika II. kategória végeredménye     1. Horváth György (Fazekas M. Fővárosi Gyakorló Gimn., 12. évf.),  tanárai: Takács Lajos, Horváth Gábor; 2. Gáspár Merse Előd (Fazekas M. Fővárosi Gyakorló Gimn., 12. évf.),  tanára: Horváth Gábor; 3. Buruzs Ádám (Szeged, Radnóti M. Kísérleti Gimn., 12. évf.),  tanárai: Mike János, Hilbert Margit;   4. Varjú Péter (Szeged, Radnóti M. Kísérleti Gimn., 11. évf.), tanára: Dudás Zoltánné; 5. Pozsgay Balázs (Pécs, Magyar-német Nyelvű Iskolaközp. 11. évf.), tanárai: Baumgartner Annamária, Kotek László; 6. Nagy István (Debrecen, KLTE Gyak. Gimn., 12. évf.), tanára: Dudics Pál; 7. Kiss Gergely (Fazekas M. Főv. Gyak. Gimn., 12. évf.), tanára: Horváth Gábor; 8. Horváth Balázs (Debrecen, KLTE Gyak. Gimn., 12. évf.), tanára: Horváth Henrietta; 9. Sáfár Szilveszter (Szeged, JATE Ságvári E. Gyak. Gimn., 12. évf.), tanára: Tóth Károly; 10. Jurányi Zsófia (Pécs, Leöwey Klára Gimn. 11. évf.), tanárai: Simon Péter, Kádár Gézáné, Kotek László.       A fizika III. kategória végeredménye     1. Patay Gergely (Debrecen, Tóth Árpád Gimn., 12. évf.),  tanárai: Kovács Miklós, Szegedi Ervin; 2. Schmidt András (Budapest, Szent István Gimn., 11. évf.),  tanára: Moór Ágnes; 3. Máthé András (Budapest, ELTE Apáczai Csere J. Gyakorló Gimnáziuma 12. évf.),  tanára: Flórik György;   4. Hegedűs Ákos (Pécs, Cisztersi Rend Nagy Lajos Gimn. 12. évf.), tanárai: Orovica Márkné, Kotek László; 5. Nagy Ádám (Budapest, Szent István Gimn., 11. évf.), tanára: Moór Ágnes; 6. Szilágyi Tamás (Debrecen, KLTE Gyak. Gimn., 11. évf.), tanárai: Szegedi Ervin, Szegediné Nagy Judit; 7. Nagy Zsombor (Tata, Eötvös J. Gimn. 12. évf.), tanárai: Ádám Árpád, Maknics Gyula; 8. Jung János (Bonyhád, Petőfi S. Evang. Gimn., 12. évf.), tanárai: Erdélyesi Sándor, Kotek László; 9. Bankó Krisztián (Budapest, ELTE Apáczai Csere J. Gyak. Gimn., 12. évf.), tanára: Flórik György; 10. Csige Sándor (Debrecen, KLTE Gyak. Gimn., 12. évf.), tanára: Szegedi Ervin. Holics László