|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az elméleti feladatok megoldása
1. feladat. a) A hasáb gördülése közben, az egymást követő becsapódásokkor nagy erők lépnek fel a lejtővel érintkező élek (pl. az 1.1 ábrán -val jelölt él) mentén. Ezek az erők pillanatszerűen lecsökkentik a hasáb érintés előtti szögsebességét a becsapódást közvetlenül követő értékre. Észrevehetjük azonban, hogy a hasábra ható erők nem változtatják meg az pontra számítható perdületet, ami saját- és pályaperdületből áll: Az tehetetlenségi nyomaték megadott értékének behelyettesítése után azonnal megkapjuk az eredményt:
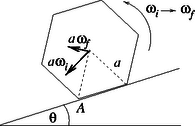 1.1. ábra 1.1. ábra
b) A test mozgási energiája az ütközés előtt is és a becsapódást követően is a hasáb egy-egy oldaléle körüli forgásból számítható. A mozgási energiák aránya: | |
c) A hasáb következő éle akkor érinti a lejtőt, ha energiája elegendő ahhoz, hogy súlypontját ,,átemelje" pályájának legmagasabb pontján. Az 1.2 ábráról leolvasható, hogy a súlypont emelkedése , ahol a lejtő hajlásszöge. Ha az érintés előtti minimális energiát alakban írjuk fel, akkor a kritikus esetre a következő egyenlet adható: | |
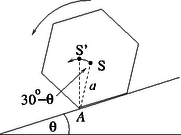 1.2. ábra 1.2. ábra
d) Tegyük fel, hogy a hasáb úgy mozog, hogy az érintés előtti mozgási energiája már felvette az állandósult értéket. Az állandósult mozgásnak az a feltétele, hogy a becsapódásonként a mozgási energia vesztesége éppen egyenlő legyen az egy-egy lépésre eső helyzeti energia csökkenéssel. Az 1.3 ábra alapján: | |
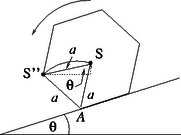 1.3. ábra 1.3. ábra
e) Minél kisebb egy lejtő hajlásszöge, annál kisebb egy-egy lépésben a hasáb helyzeti energiájának csökkenése, másrészt annál nagyobb a súlypont emelkedéséből származó ,,fékező korlát''. A kettő egyenlősége (a két előző alkérdés eredményének egybevetése) adja meg az állandósult mozgásra még alkalmas minimális hajlásszöget: amiből a kérdéses szögre meglepően kicsiny érték, adódik.
Megjegyzés. A feladat része úgy is megoldható, hogy felírjuk a a becsapódáskor bekövetkező sebesség- és szögsebesség-változásokat a fellépő erők és forgatónyomatékok segítségével. Ezek az erők olyan nagyok, hogy mellettük a hasábra ható nehézségi erő elhanyagolható.
2. feladat. a) A jég megolvasztásához szükséges hőt a Föld mélyéből érkező hőáram fedezi: ( év), amiből az évente megolvadó jégréteg vastagsága: .
b) A jégtábla alján a nyomás a külső légnyomás és a jég súlyából származó hidrosztatikai nyomás összege: | |
A jégtábla alján vékony vízréteget képzelhetünk el, ami akkor nem folyik egyik irányba sem, ha a felette lévő jégréteg nyomása megegyezik a víz nyomásával. -nál a víz nyomása , magasabban pedig a hidrosztatikai nyomásnak megfelelően kisebb: A víz és a jég nyomása akkor lesz -től függetlenül egyenlő, ha , azaz Egyensúlyi állapotban tehát a jégréteg felső felületének süllyednie kell, ha az alatta lévő talaj emelkedik (2.1 ábra).
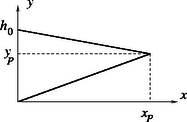
Ha a sziklatalaj menetét az egyenlet írja le, továbbá a jég vastagsága az helyen , akkor a jégfelszínt leíró egyenlet: (2.2 ábra). A két egyenes az , koordinátájú pontban metszi egymást.
 2.1. ábra 2.1. ábra
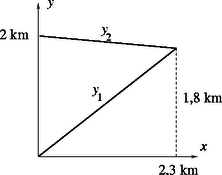 2.2. ábra 2.2. ábra
|
c) Mivel a víz sűrűsége nagyobb a jégénél, így olvadáskor a keletkezett víz kisebb térfogatot foglal el, és a jégtábla felszínén (éppen a megolvadt kúp alakú víztömeg felett) fordított kúp alakú bemélyedés jön létre. A behorpadás legnagyobb mélységét a alkérdésre adott válasz alapján számíthatjuk ki: A felszínen kialakult bemélyedést a 2.3 ábra mutatja.
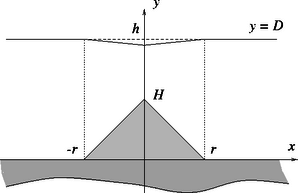 2.3. ábra 2.3. ábra
d) A jégréteg aljára behatoló forró magma miatt nagy mennyiségű jég olvad meg. A folyamatot három lépésben képzelhetjük el. Először a magma-benyomulás helyén lévő térfogatú jég olvad meg, és a keletkező víz elfolyik. Második lépésben fordított kúp alakú benyomódás jön létre a jégréteg felszínén, miközben a magma-benyomulás felett keletkező víz folyamatosan elfolyik. Ez a szakasz a nyomás-egyensúly kialakulásáig tart, a horpadás mélységét az előző alkérdésekre adott válaszok alapján számíthatjuk ki: Feltételezhetjük, hogy a magma-benyomulás anyaga még ekkor is igen meleg, tehát a magma további jégmennyiséget olvaszt meg, ami viszont már nem folyik el, hiszen a megolvadása nem befolyásolja a kialakult nyomás-egyensúlyt. A harmadik lépésben elolvadó jég térfogatát is kezelhetjük egy kúp térfogataként: , amelyből a magma-benyomulás felett magasságú ,,vízkúp" jön létre. A ,,vízkúp" tovább növeli a felszíni behorpadás mélységét, amit szintén az előző alkérdésekre adott válaszok szerint határozhatunk meg. Az olvadási folyamat végére létrejövő horpadás teljes mélységét így írhatjuk fel: amelyből a vízkúp tetőpontjának magasságát a jégtábla alapjának eredeti szintjéhez képest már könnyen kiszámíthatjuk: . A magma-behatolás magasságát kalorimetrikus egyenlet alapján határozhatjuk meg (a magma belső energiacsökkenése fedezi a jég megolvasztásához szükséges hőt): | |
A szükséges behelyettesítések és számítások elvégzése után a magma-behatolás magasságára adódik. A magma-behatolás és a visszamaradt víztömeg alakját a 2.4 ábra mutatja. A keletkezett és elfolyt víztömegeket ezek után már igen könnyű meghatározni, hiszen adja a teljes elolvadt jégtérfogatot, míg azt a jégtérfogatot, amiből a megolvadt víz elfolyt. A numerikus számítások szerint a keletkezett teljes víztömeg: , míg az elfolyt víz tömege: .
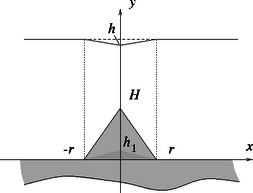 2.4. ábra 2.4. ábra
3. feladat
a) A közös centrumtól távolodó két objektum látszólagos szögsebességét könnyen meghatározhatjuk, ha látószögüket az idő függvényében ábrázoljuk, és a kapott egyenesek meredekségét leolvassuk. Ha 1-es index jelöli a bal oldali, 2-es index pedig a jobb oldali forrást, akkor rad/s, illetve rad/s értékekre jutunk. A rádióforrások transzverzális (keresztirányú) sebességét a szögsebesség és az m távolság szorzataként számíthatjuk ki: , , ahol a fénysebesség.
b) Egyszerű számításaink alapján arra a meglepő eredményre jutottunk, mintha a bal oldali objektum fénynél sebesebben (!) mozogna. A probléma körültekintőbb tárgyalása érdekében képzeljünk el egy fényforrást, ami sebességgel mozog egy tőle távoli megfigyelő irányához képest szögben (3.1 ábra). A sebesség nagyságát jelölje . A fényforrás távolságát a megfigyelő -nek méri, szögsebességét -nak észleli. Tekintsük a forrás mozgását ideig, miközben az pontból az pontba jut: .
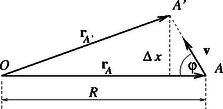 3.1. ábra 3.1. ábra
Jelölje az -ból, illetve -ből induló jelek beérkezésének időbeli különbségét az pontban. Mivel és távolsága különböző, a fénysebesség pedig véges: Kis idők esetén , tehát Mindezek figyelembe vételével Így a forrás -beli látszólagos keresztirányú sebessége | |
ahol felhasználtuk, hogy a megfigyelő vonatkoztatási rendszerében a valódi keresztirányú sebesség . Az -ban észlelhető szögsebesség:
c) Ha feltételezzük, hogy a két objektum egy egyenes mentén, azonos nagyságú sebességgel távolodik egymástól, akkor a következő összefüggéseket írhatjuk fel a látszólagos szögsebességekre: | |
A megadott, illetve mért numerikus értékek segítségével a fenti két kifejezésből egyszerű algebrai átalakításokkal és értéke kiszámítható: , . Megnyugodhatunk tehát, hiszen az észlelt rádióforrások mindössze a fénysebesség -ával mozognak.
d) A látszólagos keresztirányú sebesség akkor lehet nagyobb vagy egyenlő a fénysebességnél, ha a feltétel teljesül, ami a vizsgált esetben fenn is áll. Ez a feltétel a következő alakba írható át: A síkon az egyenlőség jelöli ki azt a tartományt, amin belül a feltétel teljesül (3.2 ábra).
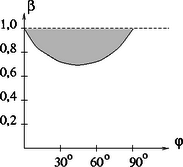 3.2. ábra 3.2. ábra
e) Könnyen meggyőződhetünk arról, hogy a alkérdés válaszában megadott kifejezésnek a fizikailag értelmes szögtartományban adott esetén akkor van maximuma, ha . Eszerint a látszólagos keresztirányú sebesség végtelenhez tarthat, ha megközelíti az 1-et, ami persze azt is jelenti, hogy nullához tart, vagyis a mozgó objektum a megfigyelő felé mozog közel fénysebességgel.
f) A relativisztikus Doppler-eltolódás egyenleteit kell kezelnünk: A szög kiejtésével kell -t kifejeznünk, amit a két egyenlet összeadásával, majd rendezésével tehetünk meg: tehát a kérdéses szám: . A alkérdésre adott válasz két egyenletében és voltak az ismeretlenek, -et más mérésekből meghatározott, adott értéknek vettük. Ha viszont a legutóbbi összefüggésünket harmadik egyenletnek tekintjük, ami közvetlenül megadja értékét, akkor mellett az távolság is meghatározható.
A kísérleti feladat megoldása
I. rész. Mágneses árnyékolás vizsgálata.
A mérésnek ebben a részében a versenyzők feladata az árnyékolást leíró (a feladat szövegében megadott) képletben szereplő együttható frekvenciafüggésének meghatározása volt. Ehhez különböző frekvenciákon különböző vastagságú aluminium fóliával kellett méréseket végezni. A mérés maga nagyon egyszerű: a rendelkezésre álló digitális műszerekkel a frekvenciát és a mérőtekercsben indukálódott feszültséget lehetett mérni ‐ itt legfeljebb a helyes méréstartomány megválasztására kellett figyelni. A versenyzőknek talán azt volt a legnehezebb eldönteni, hogy a rendelkezésre álló idő alatt hány különböző frekvencián és hány különböző fóliavastagság esetében mérjenek.
A mérési adatok kiértékelése is elég hosszadalmas munka. A megadott képlet alapján egy adott frekvencián
| |
kifejezést kapjuk, tehát ha -t függvényében ábrázoljuk, akkor az elmélet szerint a mérési pontoknak a mérés hibahatárán belül egy meredekségű egyenesen kell lenniük. Ezt a grafikont minden egyes mért frekvenciánál el kell készíteni, a mérési pontokra egyenest kell illeszteni, az egyenesek meredekségét le kell olvasni. Ezután lehet ábrázolni -t függvényében.
II. rész Mágneses fluxus-csatolás vizsgálata.
A feladat második részében a versenyzők a méréssel kapcsolatos elméleti feladatokat is kaptak. Az 1. kérdésben az önindukciós együtthatókat és a csatolási tényezőt megadó összefüggéseket kellett igazolniuk. Az önindukciós együtthatók definiciója közismert, a csatolási tényező képletét pedig a feladat szövegében megadott összefüggésekkel könnyen igazolhatjuk: amiből adódik.
A definiáló összefüggések alapján könnyen összerakhatóak a mérési kapcsolások:
 4. ábra 4. ábra
Megjegyzés. A kapcsolás megtervezésekor érdemes figyelembe venni, hogy a digitális feszültségmérők 1 M-nál nagyobb belső ellenállásukkal ,,sokkal ideálisabbak", mint az árammérők.
A 2. és 3. kérdésre ehhez hasonlóan, a feladat szövegében megadott összefüggésekbe való behelyettesítéssel és rendezéssel lehet válaszolni. Ezt az olvasóra bízzuk. A keresett összefüggések: | |
A 4. és az 5. feladat két korábbi feltevés számszerű igazolása volt. Az önindukciós együttható menetszámtól való függését három eredmény (, és ) összevetésével igazolhatjuk. Az érték mindhárom esetben hibahatáron belül megegyezik. A primer tekercs 2‐3 -os ohmos ellenállása pedig valóban elhanyagolható a tekercs induktív ellenállásának kb. -os értékéhez képest.
A 6. feladat a ferritmag relatív permeabilitásának meghatározása volt. A ferritmagon vékony papírlapok segítségével két rést lehetett létrehozni. Az Ampre-féle gerjesztési törvényt alkalmazva mindkét esetre: | |
Felhasználva, hogy , illetve és hogy , illetve azt kapjuk, hogy ahol a ferritmag középvonalának hossza, pedig a papír vastagsága. numerikus értékének meghatározásához a geometriai adatokon kívül már csak a rést tartalmazó vasmagon lévő tekercs önindukciós együtthatóját kellett megmérni.
A feladatok szövege múlt havi számunkban olvasható. |
|
 PDF | MathML
PDF | MathML