|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.
1. feladat. Szabályos hatszög alapú hasáb gördülése
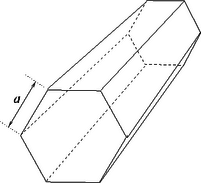 1.1. ábra. Egy szabályos hatszög keresztmetszetű hasáb 1.1. ábra. Egy szabályos hatszög keresztmetszetű hasáb
Tekintsünk egy hosszú, merev, szabályos hatszög alapú egyenes hasábot, amilyen pl. egy ceruza (1.1 ábra). A homogén sűrűségű hasáb tömege . A szabályos hatszög mindegyik oldaléle . A hatszögű hasáb középtengelyére vonatkoztatott tehetetlenségi nyomatéka: A hasáb egy hosszanti élére vonatkoztatott tehetetlenségi nyomatéka:
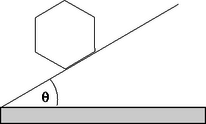 1.2. ábra. Szabályos hatszög keresztmetszetű hasáb a lejtőn 1.2. ábra. Szabályos hatszög keresztmetszetű hasáb a lejtőn
a) (3,5 pont) A hasáb kezdetben nyugalomban van, tengelye vízszintesen fekszik egy sík lejtőn, aminek a vízszintessel képezett hajlásszöge kicsi (1.2 ábra). Tételezd fel, hogy a henger oldallapjai enyhén konkávak, így a hasáb csak oldalélei mentén érinti a lejtőt. (Ennek a csekély behajlásnak a tehetetlenségi nyomatékra gyakorolt hatását elhanyagolhatjuk.) A hasábot mozdítsuk ki nyugalmi állapotából, így az egyenetlen mozgással legurul a lejtőn. Feltételezzük, hogy a súrlódás bármilyen csúszást megakadályoz, valamint hogy a hasáb mindvégig érintkezik a lejtővel. Mielőtt egy adott él éppen megérinti a lejtőt, a szögsebesség legyen , közvetlenül az él és a lejtő érintkezése után pedig . Mutasd meg, hogy és írd az együttható értékét a válaszlap megfelelő rovatába!
b) (1 pont) A hasáb mozgási energiája közvetlenül az érintés előtt és közvetlenül utána . Mutasd meg, hogy és az együttható értékét írd a válaszlap megfelelő rovatába!
c) (1,5 pont) Ahhoz, hogy egy következő él is érintse a lejtőt, -nek nagyobbnak kell lennie egy minimális értéknél. Ez utóbbi így írható: Itt a nehézségi gyorsulás. Határozd meg -t a lejtő hajlásszögének és az együtthatónak a függvényeként.
d) (2 pont) Ha a alkérdés feltétele teljesül, akkor a mozgási energia egy meghatározott értékhez tart, miközben a hasáb gördül a lejtőn. Annak ismeretében, hogy ez a határérték létezik, mutasd meg hogy így írható:
Fejezd ki értékét és függvényeként.
e) (2 pont) Számítsd ki pontossággal, hogy mi a lejtő hajlásszögének az a minimuma, amelynél az egyenetlen gördülés ‐ ha egyszer elindult ‐ végtelen hosszan folytatódni fog.
2. feladat. Víz a jégmező alatt.
A jégmező szilárd talajon helyezkedik el, függőleges vastagsága néhány km, vízszintes kiterjedése többször 10 vagy 100 km. A feladatban a jég olvadását fogjuk tanulmányozni, és azt, hogy miként viselkedik a víz hőmérsékletű jégtömb alatt. Feltételezzük, hogy ilyen feltételek mellett a nyomásváltozások a jégben (akárcsak viszkózus folyadékban) lényegében függőleges elmozdulásokat okoznak.
E feladat megoldásánál a következő adatokat használhatod: a víz sűrűsége: , a jég sűrűsége: , a jég fajhője: , a jég olvadáshője: Lj=3,4⋅105J/kg, a kőzet és a magma sűrűsége: ϱk=2,9⋅103kg/m3, a kőzet és a magma fajhője: ck=700J/(kg∘ C), a kőzet és a magma olvadáshője: Lk=4,2⋅105J/kg, a Föld felületén kilépő átlagos hőáramsűrűség: JQ=0,06W/m2, a jég olvadáspontja: T0=0∘C, állandó.
a) (0,5 pont) Tekints egy vastag jégmezőt, amely alatt hő áramlik fel a Föld mélyéből. A fenti adatokat használva számítsd ki, hogy évente milyen d vastagságú jégréteg olvad el!
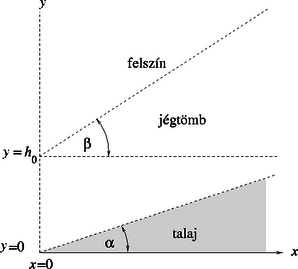 2.1. ábra. Lejtőn lévő sík felszínű jégtömb keresztmetszete 2.1. ábra. Lejtőn lévő sík felszínű jégtömb keresztmetszete
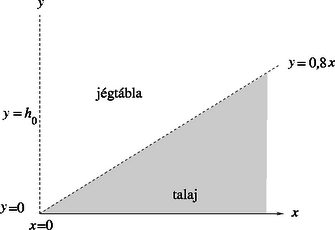 2.2. ábra. Egy 0∘C hőmérsékletű jégtábla úgy nyugszik egy sziklalejtőn, hogy a jég alatt a víz egyensúlyban van 2.2. ábra. Egy 0∘C hőmérsékletű jégtábla úgy nyugszik egy sziklalejtőn, hogy a jég alatt a víz egyensúlyban van
|
b) (3,5 pont) Tekintsük egy jégtömb felső, sík felszínét. A jégtábla alatt a szikla-lejtő hajlásszöge α. A jégtábla sík felszínének hajlásszöge β (2.1 ábra). A jég függőlegesen mért vastagsága az x=0 helyen h0. Eszerint a jégtáblát alul és felül határoló síkok egyenlete: | y1=x⋅tgα,y2=h0+x⋅tgβ. | (2.1) |
Fejezd ki a p nyomást a jégtábla alján az x vízszintes koordináta függvényeként. Ezt a képletet írd a válaszlapra! Fogalmazd meg matematikailag α és β függvényében annak feltételét, hogy a jégtábla és a sziklatalaj közt a víz ne folyjék egyik irányba sem. Mutasd meg, hogy ez a feltétel tgβ=s⋅tgα alakban írható. Határozd meg az s együtthatót, és eredményedet képlet formájában add meg!
A 2.2 ábrán az y1=0,8x vonal a sziklatalaj menetét mutatja a jégtábla alatt. A jég függőlegesen mért h0 vastagsága az x=0 helyen 2 km. Tételezzük fel, hogy a víz a jégtábla alatt egyensúlyban van.
A válaszlapon rajzold be az y1 egyenest, és rajzold fölé a jégtábla felszínét jelző y2 egyenest is. Jelezd az ábrán, melyik vonal melyiket jelenti!
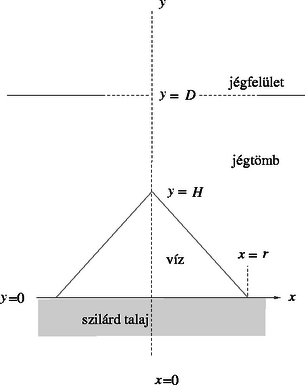 2.3. ábra. A jégben kialakult vízkúp függőleges keresztmetszete 2.3. ábra. A jégben kialakult vízkúp függőleges keresztmetszete
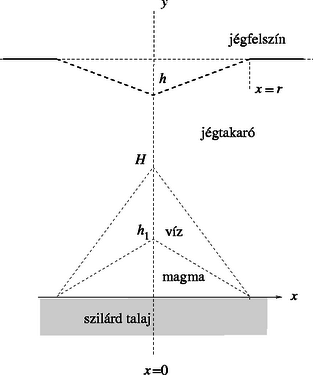 2.4. ábra. A kúp alakú jég-bemélyedés centrális függőleges síkmetszete 2.4. ábra. A kúp alakú jég-bemélyedés centrális függőleges síkmetszete
(Az ábra nem méretarányos!)
|
c) (1 pont) Vízszintes talajon elhelyezkedő nagykiterjedésű jégtábla kezdetben D=2,0km vastag. Ekkor a jég viszonylag gyors megolvadása révén egy H=1,0km vastag, r=1,0 km sugarú, kúp alakú víztömeg alakul ki (2.3 ábra). Tételezzük fel, hogy a visszamaradt jégtömeg ehhez az új állapothoz úgy alkalmazkodik, hogy benne csak függőleges elmozdulások mennek végbe. Vezesd le képletekkel üres, tiszta lapon, és rajzold le a válaszlap ábra-ablakába a jégtábla felső felületének alakját a vízkúp képződése és a hidrosztatikus egyensúly beállta után.
d) (5 pont) Egy nemzetközi kutatócsoport expedíciói évente megvizsgálják az Antarktisz 0∘C hőmérsékletű jégtakaróját. Ennek felszíne normálisan egy vízszintes felületű, kiterjedt jégréteg. De most egy mély, kráterszerű mélyedésre bukkannak, ami olyan, mint egy felfordított kúp, amelynek legnagyobb h bemélyedése 100m és r sugara 500m (2.4 ábra).
Tapasztalataikat megbeszélve a kutatók arra a következtetésre jutnak, hogy a jég alatt kisebb vulkánkitörés történhetett. Egy kevés olvadt magma benyomult a jégréteg aljába, ott megdermedt és lehűlt, eközben bizonyos mennyiségű jeget megolvasztott. A kutatók megpróbálják megbecsülni a behatolt magma térfogatát, hogy megértsék, mitől lett a megolvadt víz. Gondolatmenetük a következő:
Tételezzük fel, hogy a jégben csak függőleges mozgás ment végbe. Azt is tételezzük fel, hogy a behatoló magma 1200∘C hőmérsékleten teljesen folyékony állapotú volt. Az egyszerűség kedvéért még azt is feltehetjük, hogy a benyomulás kúp alakban történt, körszerűen a megfigyelt kúpos jég-bemélyedés alatt. A magma behatolása viszonylag rövid idő alatt ment végbe a hőkicserélődés időigényéhez képest. A hőátadás kezdetben elsősorban függőleges irányú volt, így a jégből kiolvadt térfogat mindig kúp alakú volt, a kúp tengelye pedig a magma-benyomulás centrumán átmenő függőleges volt.
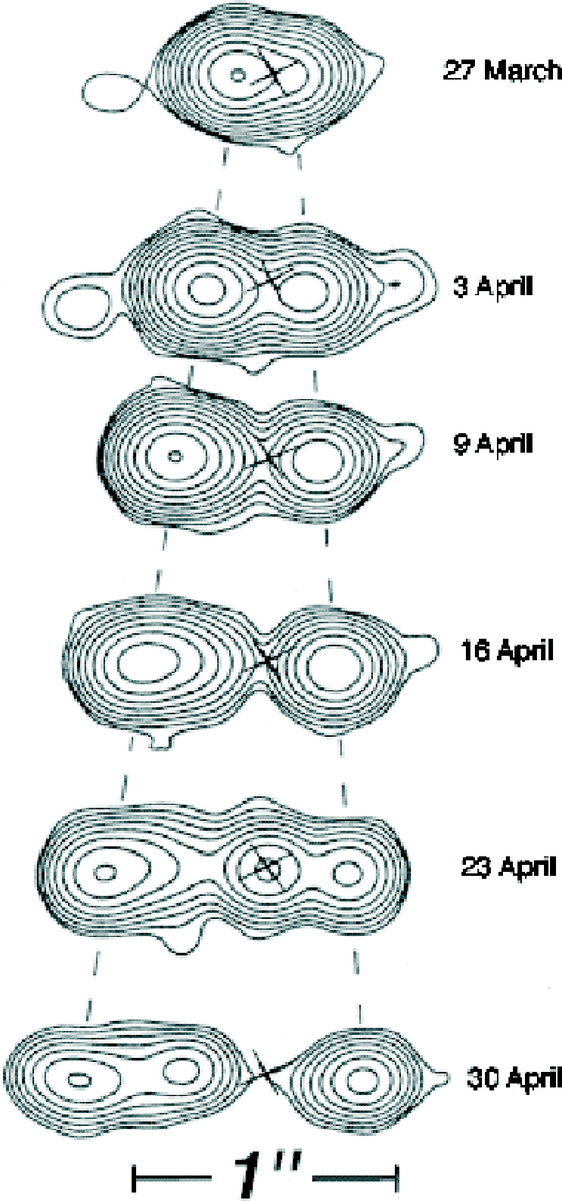 3.1. ábra. Tejútrendszerünk egyik rádióforrásának emissziója 3.1. ábra. Tejútrendszerünk egyik rádióforrásának emissziója
Ezen feltételek mellett a jég megolvadása két lépésben ment végbe. Először a víz nincs nyomás-egyensúlyban a magma fölött, hanem elfolyik onnan. Az elfolyó víz 0∘C hőmérsékletűnek tételezhető fel. Később beáll a hidrosztatikai egyensúly, a víz a keletkezési helyén, a magma-benyomulás felett marad, nem folyik el. Számítsd ki a következő mennyiségeket a hőmérsékleti egyensúly beálltakor, és írd ezeket a válaszlapra:
1. A jégtakaró alatt kialakult vízkúp tetőpontjának H magassága a jégtábla alapjának eredeti szintjéhez képest.
2. A magmabehatolás h1 magassága.
3. A keletkezett víz teljes mt tömege és az elfolyt víz m' tömege.
Milliméterpapíron ábrázold méretarányosan a magma-behatolás és a visszamaradt víztömeg alakját! A 2.4 ábra által sugallt koordináta-rendszert használd!
3. feladat. Fénynél sebesebben?
Ebben a feladatban egy 1994-ben elvégzett mérést elemzünk és értelmezünk. A mérés egy a Tejútrendszerben lévő összetett forrás rádióhullámú sugárzására vonatkozik. A szélessávú vevőantenna centiméteres hullámhosszú rádióhullámokra volt hangolva. A 3.1 ábra azt mutatja, hogy különböző időpontokban milyen képet láttak. A ,,szintvonalak" az azonos intenzitásokat jelzik, mint ahogyan a földrajzi térkép szintvonalai az azonos magasságú pontokat kötik össze. A képen látható és szaggatott vonalakkal érzékeltetett két maximumot úgy értelmezik, hogy két objektum távolodik egy közös centrumtól. Ezt a centrumot keresztek jelzik az ábrákon. (A centrumról feltételezik, hogy nyugszik a térben; ez is erős rádióforrás, de főleg más hullámhosszon sugároz.) A méréseket több, mint egy hónapon át mindig azonos napszakban, azonos órában végezték el. Az ábra léptékét egy skálaszakasz jelzi, ami 1 ívmásodpercnek felel meg (1 ívmásodperc = 1 arc sec = 1 as = 13600 szögfok). A centrumban lévő kereszttel jelölt égitest becsült távolsága R=12,5 kpc. Egy kiloparsec (kpc) 3,09⋅1019 m-nek felel meg. A fény sebessége: c=3,00⋅108 m/s. A feladat megoldásában nem kell hibaszámítást végezni.
a) (2 pont) A két kidobott rádióforrás szögtávolságát a centrumtól θ1(t) és θ2(t) jelöli. (Jelölés: 1 a bal oldali, 2 a jobb oldali forrás, t a megfigyelés ideje.) A Földről látszó szögsebességek ω1 és ω2. A két rádióforrásnak megfelelő transzverzális (keresztirányú) sebességek: v'1,⊥ és v'2,⊥. A 3.1 ábra alapján határozd meg ω1 és ω2 értékét ezred-ívmásodperc/nap egységekben. Határozd meg v'1,⊥ és v'2,⊥ számértékeit is. (Némelyik eredményt meglepőnek fogod találni.)
b) (3 pont) Az előző alkérdésben támadt probléma feloldása érdekében képzelj el egy fényforrást, ami v→ sebességgel mozog egy tőle távoli O megfigyelő irányához képest φ szögben (0≤φ≤π). A sebesség nagyságát jelölje v=βc, ahol c a fénysebesség. A fényforrás távolságát a megfigyelő R-nek méri, a fényforrás szögsebességét ω-nak észleli. A látásirányra merőleges látszólagos sebesség v'⊥.
Határozd meg ω és v'⊥ értékeit β, R és φ függvényében!
c) (1 pont) Feltételezzük, hogy az a) alkérdésben szereplő két kidobott objektum egymáshoz képest ellenkező irányban mozog, szétrepülési sebességük egyenlő, v=βc. Ekkor a b) alkérdés eredményei alapján β és φ kiszámítható az ω1 és ω2 szögsebességek, valamint az R távolság ismeretében. Itt φ a b) alkérdésben értelmezett szög a bal oldali objektumra vonatkozóan, ami az a) alkérdésben az 1 indexnek felel meg. Vezess le képleteket arra, hogyan kell ismert mennyiségekből kiszámítani β és φ értékét. Határozd meg β és φ értékét az a) alkérdésben megadott számértékek alapján.
d) (2 pont) A b) alkérdés szerinti egy-test esetben keresd meg annak feltételét, hogy a látszólagos v'⊥ transzverzális sebesség nagyobb legyen, mint a c fénysebesség. Írd ezt a feltételt β>f(φ) alakba, az f függvényre keress analitikus alakot, és add meg azt a válaszlapon! Rajzold le a (β,φ) koordinátasík fizikailag értelmes tartományát. Satírozd be azt a tartományt, ahol v'⊥>c teljesül.
e) (2 pont) A b) alkérdésben tárgyalt egy-test esetben találj egy képletet a v'⊥ látszólagos transzverzális sebesség maximális (v'⊥)max értékére adott β esetén! észreveheted, hogy ez a maximális látszólagos transzverzális sebesség minden határon túl nőhet, ha β→1.
f) (1 pont) Az R értékére vonatkozóan a bevezetőben megadott becsült érték nem megbízható. Ezért a kutatók azon kezdtek gondolkozni, hogy létezik-e jobb és közvetlenebb módszer R meghatározására. Az egyik ötlet a következő:
Tételezd fel, hogy a két kidobott tárgy színképében azonosítjuk és megmérjük egy színképvonal Doppler-eltolódott λ1 és λ2 hullámhosszait, ami nyugvó objektum sugárzása esetén λ0 volna. Indulj ki a relativisztikus Doppler-eltolódás képletéből:
Mint korábban, most is tételezd fel, hogy a két tárgy sebessége ugyanolyan nagyságú. Mutasd meg, hogy az ismeretlen β=v/c kifejezhető λ0, λ1 és λ2 függvényeként a következő képlettel: Írd be az α együttható számértékét a válaszlap megfelelő ablakába. észreveheted, hogy ily módon a hullámhosszak mért értékéből gyakorlati becslést kaphatsz az R távolságra.
Rendelkezésre álló eszközök: Alaplap 6 banándugó hüvellyel; az alaplapba beépített mérőtekercs; U alakú ferritmag A és B jelű tekerccsel; U alakú ferritmag tekercs nélkül; 25 μm, 50 μm és 100 μm vastag alumínium fólia; jelgenerátor részletes használati utasítással; két multiméter (részletes leírással); 6 db röpzsinór banándugóval; 2 db gumigyűrű és 2 kis darab pauszpapír.
I. örvényáramok mágneses árnyékolása (8 pont)
Időben változó mágneses terek vezetőkben örvényáramokat keltenek. Az örvényáramok viszont ellentétes mágneses teret hoznak létre. Közönséges fémekben a véges vezetőképesség miatt a mágneses tér leárnyékolása nem tökéletes. Az alumínium fólia leárnyékolását fenomenológiailag (tapasztalatok alapján) a képlettel írjuk le. B a mágneses indukció az alumínium fólia árnyékolása alatt. B0 a mágneses indukció ugyanezen a helyen, ha nincs jelen fólia, α az árnyékolási együttható és d a fólia vastagsága.
A mérés
A ferritmagot, amelyen a tekercsek vannak, talpaival lefelé úgy állítsd a kiemelkedő fatuskóra, hogy az A tekercs pontosan az alaplapba épített mérőtekercs felett legyen. A vasmagot rögzítsd az alaplapra a gumigyűrűvel, ami a tekercset a fatuskó alatt átvezetve az alaplaphoz köti. Feltételezheted, hogy az alumínium vastagságának és a frekvenciamérésnek elhanyagolható a hibája.
1. (1 pont) Az A és B tekercs csatlakoztató végződéseit vezesd el a banándugó-hüvelyekhez, és mérd meg mind a három tekercs ellenállását abból a célból, hogy biztos lehess, hogy jók a csatlakozások. 10 Ω-nál kisebb ellenállásértékeket várhatsz.
2. (5 pont) Gyűjts mérési adatokat, hogy ellenőrizd a fent megadott modell-képletet, és határozd meg a (25‐175 μm vastag) alumínium fóliák α árnyékolási faktorát a 6‐18 kHz frekvenciatartományban. Az alumínium fóliákat a mérőtekercs fölé helyezd úgy, hogy a fóliák az alaplapon bejelölt téglalapot fedjék. Az A tekercsre szinuszos váltófeszültséget kapcsolj!
3. (2 pont) ábrázold α értékeit az f frekvencia függvényében!
II. Mágneses fluxuscsatolás (12 pont)
Azt tanulmányozzuk, hogy két tekercs, melyek közös ferritmagja zárt, hogyan reagál egy külső Ug váltófeszültségre, amit egy szinuszos jelgenerátor ad. Az általad használt berendezésben minden mágneses telítődési jelenség elhanyagolható. Ezen kívül azt is feltételezheted, hogy a ferrit μ mágneses permeabilitása állandó.
Elméleti háttér
Az itt következő elméleti tárgyalásban és az adatok elemzésében is feltételezzük, hogy a két tekercs ohmikus ellenállása és a ferritmag hiszterézis-jelensége elhanyagolható befolyást gyakorol a mért áramerősségekre és feszültségekre. Ezen egyszerűsítések miatt az alábbi tárgyalásban a mért és számított értékek között bizonyos eltérések jelentkezhetnek.
Egy tekercs esete
Először tekintsük egy I áram által átjárt tekercs magját. Az a Φ mágneses fluxus, amit az áram a tekercsben lévő ferritmagban kelt, arányos az I áramerősséggel és az N menetszámmal. A fluxus még egy g geometriai tényezőtől is függ, ami a vasmag nagyságától, alakjától és μ=μrμ0 permeabilitásától függ. (A mágneses permeabilitás a mag anyagának mágneses tulajdonságait írja le. A relatív permeabilitás jele μr, a vákuum permeabilitása μ0.) A Φ mágneses fluxust a képlet adja meg, ahol c=μg. Az indukált feszültség a Faraday-féle indukciótörvényből kapható: | U(t)=-NdΦ(t)dt=-cN2dI(t)dt. | (3) |
Egy L önindukciós együtthatójú tekercsben az áramerősség és a feszültség kapcsolatát az összefüggéssel szokás leírni. A tekercsre kapcsolt szinuszos jelgenerátor áramot hajt át rajta, ahol ω a körfrekvencia és I0 az áram amplitúdója. A (3) egyenlet szerint ez a váltóáram a tekercsben váltófeszültséget indukál. Az áram olyan lesz, hogy az indukált feszültség megegyezzen a jelgenerátor Ug feszültségével. Az áram és a feszültség közötti fáziskülönbség 90∘-os. Ha csak a váltófeszültség és váltóáram U0, ill. I0 amplitúdóját tekintjük és a fáziskülönbséget elhagyjuk, az összefüggésünket így írhatjuk: (A továbbiakban a 0 alsó indexet elhagyjuk.)
Két tekercs esete
Most tételezzük fel, hogy egy ferritmagon két tekercs van. A ferrit vasmag arra használható, hogy csatolja a mágneses fluxust a tekercsek között. Ideális vasmag esetén a fluxus a mag bármely keresztmetszetén ugyanakkora. Valóságos magok esetében a tapasztalat azt mutatja, hogy a fluxusszóródás miatt a szekunder tekercsen kisebb fluxus lesz, mint a fluxust létrehozó tekercsen. A B szekunder tekercs ΦB fluxusa és az A primér tekercs ΦA fluxusa ezek szerint a következő kapcsolatban van: Ugyanígy a B-ben folyó áram által keltett ΦB fluxus az A tekercsben ΦA=k⋅ΦB fluxus-összetevőt fog kelteni. A k csatolási tényező 1-nél kisebb. A mérés során tanulmányozandó ferritmagon két tekercs van transzformátor elrendezésben. Tételezzük fel, hogy az A (primer) tekercset kapcsoljuk a jelgenerátorra. Ha a B tekercsben nem folyik áram (IB=0), akkor az IA által indukált UA feszültség azonos nagyságú és ellentétes Ug-vel. Az IA által a szekunder tekercsben keltett fluxus a (8) képletből számolható. Így a B tekercsben indukált feszültség:
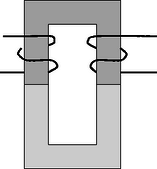 4. ábra. Transzformátor zárt mágneses körrel 4. ábra. Transzformátor zárt mágneses körrel
Ha a B tekercsben IB áram folyik, akkor az az A tekercsben feszültséget indukál, amit az előző összefüggéshez hasonlóan határozhatunk meg. Az A tekercs teljes feszültségét így a következő képlet adja meg: | Ug=UA=ωcNA2IA-ωkcNANBIB. | (10) |
A szekunder tekercs árama tehát a primer tekercsben ellentétes feszültséget indukál, ami IA növekedését okozza. Hasonló összefüggés írható fel UB-re is. Mérésekkel igazolható, hogy k értéke független attól, hogy melyik tekercset választjuk primer tekercsnek.
A mérés
A két U alakú ferritmagot illeszd össze a 2. ábrán látható módon, és rögzítsd őket a gumigyűrűkkel. állítsd be a jelgenerátort úgy, hogy 10 kHz-es szinuszos hullámot adjon. Gondolj arra, hogy a multimétereket az egyes méréseknél az ott alkalmazható legérzékenyebb méréshatárban használd. Az A és a B tekercs menetszáma: NA=150, NB=100 (±1 menet tekercsenként).
1. (3,5 pont) Bizonyítsd be, hogy az LA és LB önindukciós együtthatókra, valamint a k csatolási tényezőre a következő összefüggések érvényesek: | LA=UAωIA,IB=0,LB=UBωIB,IA=0,k=NBIBNAIA,UB=0. |
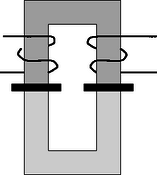 5. ábra. A ferritmagok a két távtartóval 5. ábra. A ferritmagok a két távtartóval
A válaszlap 1.a ablakában utalj bizonyításod lényegére! A válaszlap 1.b ablakába rajzold le azokat az áramköröket, melyek segítségével LA, LB és k meghatározható! A mérés elvégzése után számítsd ki LA, LB és k számértékét, és értéküket írd a válaszlap 1.c ablakába!
2. (2 pont) Amikor a szekunder tekercs rövidre van zárva, a primer tekercs Ip áramerőssége növekedni fog. Az előzőekben ismertetett egyenletek alapján add meg, hogy Ip hogyan függ a primer feszültségtől, a primer tekercs önindukciós együtthatójától és a k csatolási tényezőtől. Válaszodat írd a válaszlap 2.a ablakába! Mérd meg Ip értékét, a kapott adatot írd a válaszlap 2.b ablakába!
3. (2,5 pont) Az A és a B tekercset kétféleképpen kapcsolhatjuk sorba: úgy, hogy a két fluxusjárulék összeadódjék, vagy levonódjék egymásból.
3.1. Számítsd ki a sorbakapcsolt tekercsek LA+B önindukciós együtthatóját a mért adatok alapján arra az esetre, amikor a két tekercs I árama által létrehozott fluxusok összeadódnak (erősítik egymást). Válaszodat írd a válaszlap 3.1 ablakába.
3.2. Mérd meg a UA és UB feszültséget arra az esetre, amikor a két tekercs fluxusai ellentétesek. Mért adataidat írd a válaszlap 3.2a ablakába. A két feszültség hányadosát írd a 3.2b ablakba. Vezess le egy képletet a két tekercsre vonatkozó feszültségek hányadosára a menetszámok és a csatolási tényező segítségével, és válaszodat írd a 3.2c ablakba.
4. (1 pont) Eredményeid alapján igazold, hogy egy tekercs önindukciós együtthatója menetszámának négyzetével arányos. Eredményedet írd a válaszlap 4. ablakába!
5. (1 pont) Igazold, hogy jogos volt a primer tekercs ohmos ellenállásának elhanyagolása. érvelésedet matematikai kifejezések alakjában írd a válaszlap 5. ablakába.
6. (2 pont) Ha vékony papírlapokat illesztünk a két fél ferritmag közé (ahogy ezt a 2. ábra mutatja), akkor a tekercs önindukciós együtthatója jelentősen lecsökken. Ezt a csökkenést felhasználva határozd meg a ferrit-anyag μr relatív permeabilitását. Ehhez használd fel az Ampre-féle gerjesztési törvényt, továbbá azt a tényt, hogy a B mágneses indukció nem változik meg a ferrit‐papír határfelületen. Tételezd fel, hogy a papír relatív permeabilitása egységnyi, vagyis μ=μ0=4π⋅10-7 Ns2/Cb2, továbbá a papír vastagsága 43 μm. A geometriai tényező meghatározásánál használd az Ampre-féle gerjesztési törvényt: ahol Iteljes az integrációs út által kifeszített felületet átmetsző áramok összege. Írd be μr-re kapott algebrai kifejezésedet a válaszlap 6.a ablakába, számszerű értékét pedig a 6.b ablakba.
A feladatok megoldását következő számunkban közöljük. Addig olvasóink (elsősorban a versenyekre készülők) kipróbálhatják tudásukat. Az olimpián 5 óra állt a versenyzők rendelkezésére, és a megoldásukat egy ún. válaszlapon adták be.Az olimpián 5 óra állt a versenyzők rendelkezésére. |
|
 PDF | MathML
PDF | MathML 







