|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A feladatok megoldását a novemberi számunkban közöljük.
A mérési feladat kidolgozására 5 óra állt a versenyzők rendelkezésére.
Torziós inga
Ebben a kísérletben egy meglehetősen összetett mechanikai rendszert ‐ egy torziós ingát ‐ akarunk tanulmányozni. Amikor az inga tengelye vízszintes, fellép a bifurkáció jelensége, amit később megmagyarázunk.
Rendelkezésre álló eszközök:
| * | ‐Egy torziós inga, amely egy belül menetes (hosszában inhomogén, nem-egyenletes tömegeloszlású) csőből, egy külső menetes rúdból, valamint egy tartóállványból áll (1. ábra). |
| * | ‐Acélhuzal feszítőhurokkal. |
| * | ‐Egy hosszabb, hatszögletű, menetes furattal ellátott rudacska, amely a menetes rúdra csavarható (ez csak az utolsó kísérlethez szükséges). |
| * | ‐Egy egyenes vonalzó és egy derékszögű vonalzó. |
| * | ‐Hatszögletű, alakban meghajlított csavarkulcsok. |
| * | ‐A3 méretű milliméterpapírok. |
| * | ‐Egy állítható asztalos-szorító. |
| * | ‐Egy T keresztmetszetű alumínium idom. |
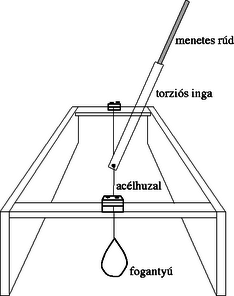 1. ábra. 1. ábra.
A kísérleti berendezést az 1. ábra mutatja. Ez egy torziós inga, amely lengésbe hozható akár vízszintesre, akár függőlegesre állított tengelye körül. A forgástengelyt a rövid, megfeszített acélszál határozza meg. Az ingatest belső része egy menetes rúd, amely ki- vagy becsavarható, és egy kisméretű, hatlapú anyacsavarral bármely helyzetben rögzíthető. Ez a menetes rúd nem vehető ki az ingatestből. A berendezés összeállításánál (az e) alkérdésnél) az acélhuzalt át kell vezetni a sárgaréz szorítólapok között és az ingatesten lévő lyukon, majd megfeszített állapotban rögzíteni kell. Először az egyik végét rögzítsd, majd a feszítőhurok segítségével feszítsd meg, és végül rögzítsd a másik végét is. Az ingatest a huzalhoz egy mélyen elhelyezett kicsi csavarral rögzíthető a kis csavarkulccsal.
Figyelem: A huzal megfeszítése csak az inga stabilitását szolgálja. Nincs szükség körülbelül 30 N-nál nagyobb feszítőerőre. Feszítés közben a huzal ne törjön meg az állványon, mert elszakadhat.
Az inga lengéseit jellemző változók:
| * | ‐az inga helyzetét a szög határozza meg, melyet a keret síkjára merőleges iránytól mérünk (az 1. ábrán a keret síkja vízszintes); |
| * | ‐a menetes rúd külső, szabad vége és az inga forgástengelye közötti távolság; |
| * | ‐az inga lengéseinek periódusideje. |
A rendszert jellemző paraméterek:
| * | ‐az acélszál csavarási rugalmas állandója (direkciós nyomatéka), melyet a következő összefüggés definiál: ; |
| * | ‐az ingatest két részének és tömege (1: belső menetes cső a kis rögzítő csavaranyával együtt és 2: menetes rúd); |
| * | ‐az egyes ingadarabok tömegközéppontjainak a forgástengelytől mért és távolsága (1: belső menetes cső és 2: menetes rúd). A mozgatható vékony menetes rúd homogén tömegeloszlásúnak tekinthető, és így a rúd hosszával és az távolsággal kifejezhető. |
| * | ‐az ingatest két részének (1: belső menetes cső és 2: menetes rúd) tehetetlenségi nyomatékai és (az angol elnevezésnek megfelelően). Most is feltételezhetjük, hogy a mozgatható menetes rúd homogén tömegeloszlásúnak tekinthető, és így a menetes rúd tömegével, a rúd hosszával és az távolsággal kifejezhető. tehát a többi paraméter egyszerű függvénye. |
| * | ‐az a szög, amelynél a visszatérítő rugalmas forgatónyomaték nulla. (Ezt a szöget az ingatest hossztengelye és a keret síkjára merőleges irány között mérhetjük.) Az ingatest a forgástengelyt szolgáltató huzalhoz a menetes rúddal ellentétes végén egy hatlapfejű csavarral rögzíthető; ezért a berendezés bármely újabb beállításánál megváltozhat. |
összefoglalva, a rendszert 7 paraméter jellemzi: , , , , , , , de mivel a berendezés minden beállításánál megváltozik, így közülük ténylegesen csak 6 mennyiség állandó. A mérés célja ezen 6 mennyiség, nevezetesen , , , , , kísérleti meghatározása.
Két tényt vegyél figyelembe: A menetes rudat nem lehet teljesen kicsavarni az ingatest csövéből. Az ingatest két részének együttes tömege megadott adat, ami az ingára rá van nyomtatva.
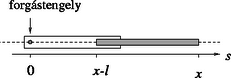 2. ábra. A mérés kiértékelésénél egy vékony, hosszú rúd tehetetlenségi nyomatékát a (2) egyenletből számíthatjuk ki. A tehetetlenségi nyomatékot az koordinátájú forgástengelyre vonatkoztatjuk. 2. ábra. A mérés kiértékelésénél egy vékony, hosszú rúd tehetetlenségi nyomatékát a (2) egyenletből számíthatjuk ki. A tehetetlenségi nyomatékot az koordinátájú forgástengelyre vonatkoztatjuk.
Ebben a kísérletben számos mennyiség valamilyen változó lineáris függvénye, és neked az a feladatod, hogy ezeknek a lineáris függvényeknek a paramétereit határozd meg. Lineáris illesztés alkalmazását ajánljuk, de más módszerek használata is elfogadható. A paraméterek mérési bizonytalanságát a lineáris illesztés alapján becsülheted meg, vagy a mérési adatok szórásából következtethetsz rájuk. A kiértékeléshez szükséged lesz a menetes rúd forgástengelyre vonatkoztatott tehetetlenségi nyomatékára. Elhanyagolva a keresztirányú méreteket a rúd hosszához képest (2. ábra), a kérdéses tehetetlenségi nyomatékot a következő formula adja meg: | | (1) |
ahol a hosszegységre eső tömeg, így tehát | | (2) |
A keresett 6 paramétert (, , , , , ) az alábbi lépéseket követve határozhatod meg:
| * | a) Az össztömeg adott (az ingára rá van nyomtatva). -et és -t úgy határozhatod meg, ha megméred az ingatest közös tömegközéppontjának a forgástengelytől vett távolságát. Ehhez először vezesd le azt az egyenletet, amely megadja függvényében a tömegközéppont helyzetét, felhasználva az , , és paramétereket. (0,5 pont) |
| * | b) Ezután mérd meg -et néhány (legalább 3) értéknél A kis hatszögletű csavaranyát, melynek tömegét -be beleértjük, a menetes rúd minden egyes megmozdítása után meg kell szorítanod.! Nyilvánvaló, hogy ennél a mérésnél az ingatestet le kell szerelni a feszítőhuzalról. Méréseid és korábbi eredményed felhasználásával add meg és értékét! (3 pont) |
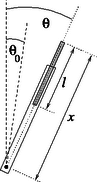 3. ábra. A és az változók, valamint a és paraméterek jelentése. 3. ábra. A és az változók, valamint a és paraméterek jelentése.
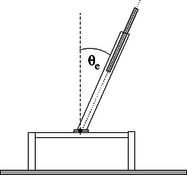 4. ábra. Ebben a kísérletben az ingatest egyensúlyi helyzete számottevően térjen el a függőlegestől! 4. ábra. Ebben a kísérletben az ingatest egyensúlyi helyzete számottevően térjen el a függőlegestől!
| * | c)Vezesd le azt az egyenletet, amely megadja az inga teljes tehetetlenségi nyomatékát az változó és az , és paraméterek függvényében. (0,5 pont) |
| * | d)Írd fel a vízszintes forgástengelyű inga mozgásegyenletét a szög és az , , , , paraméterek, valamint az teljes tehetetlenségi nyomaték és a tömegközéppont koordinátájának segítségével! (1 pont) |
| * | e) meghatározásához szereld össze az ingát, és állítsd a forgástengelyt vízszintesre. A menetes rúd kezdetben olyan mélyen legyen az ingatest furatában, amennyire csak lehet. Rögzítsd a szorítócsavarral az ingatestet az acélhuzal közepe táján úgy, hogy az egyensúlyi helyzete (melyet a súlyából származó forgatónyomaték és a rugalmas visszatérítő forgatónyomaték egyensúlya határoz meg) számottevően térjen el a függőlegestől (4. ábra). Mérd meg az egyensúlyt jellemző szöget néhány (legalább 5) értéknél! (4 pont) |
| * | f)Az előző méréssorozat alapján határozd meg értékét! (4,5 pont) |
| * | g)állítsd most az inga tengelyét függőlegesre Annak érdekében, hogy a rendszert megfelelően rögzítsd, az asztalos-szorítót áthelyezheted., és mérd meg a torziós inga lengésidejét néhány (legalább 5) értéknél. A mérési eredmények felhasználásával határozd meg és értékét! (4 pont) |
A továbbiakban, miután meghatároztad a rendszer paramétereit, a kísérleti eszközt a következő módon állítsd össze:
‐ az inga forgástengelye legyen vízszintes;
‐ a menetes rúd a lehető legmélyebben legyen az ingatestben;
‐ az inga egyensúlyi helyzete minél közelebb legyen a függőlegeshez;
‐ végül pedig csatlakoztasd a hosszabb hatszögletű rudacskát a menetes rúd végére. (Néhány menettel csavarható fel, tovább nem hajtható.)
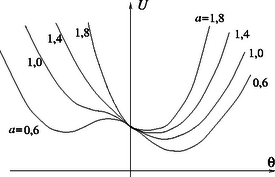 5. ábra. Az a potenciális energiával arányos függvény. A különböző görbék különböző értékeknek felelnek meg. (Esetünkben a menetes rúd helyzetével áll kapcsolatban). A csökkenő értékek esetén () bifurkáció jelenik meg. 5. ábra. Az a potenciális energiával arányos függvény. A különböző görbék különböző értékeknek felelnek meg. (Esetünkben a menetes rúd helyzetével áll kapcsolatban). A csökkenő értékek esetén () bifurkáció jelenik meg.
Ebben az összeállításban a menetes rúd helyzetétől függően az ingának két egyensúlyi helyzete is lehet. Ezt szemlélteti az 5. ábrán látható görbesereg, amely a potenciális energiát adja meg a szög függvényében. Az 5. ábrán a potenciália energia minimumhelyének megkettőződését láthatjuk, amit a matematikában bifurkációnak neveznek. Ez a jelenség különböző szimmetriák sérülésével is kapcsolatban áll, ami a részecskefizikában és a statisztikus fizikában a kutatás homlokterében áll.
Tanulmányozd a bifurkáció jelenségét úgy, hogy megméred az egyensúlyi helyzet körüli kis rezgések periódusidejét:
| * | h)ábrázold a periódusidőtLehetséges, hogy két egyensúlyi helyzetet is észlelhetsz, azonban ezek egyike stabilabb, mint a másik (lásd az 5. ábrát). Jelezd, melyik a stabilabb, és annak a periódusidejét ábrázold! függvényében! Milyen jellegű függvényt kapsz? Növekvő, csökkenő vagy ezeknél bonyolultabb függvényt? (2,5 pont) |
A feladatok kidolgozására 5 óra állt a versenyzők rendelkezésére. Megoldásaikat előre elkészített VáLASZLAPOK megfelelő rovatainak kitöltésével kellett megadniuk, elsősorban rajzok, képletek, formulák és (a feladat egyéb adatai által indokolt pontosságú) számszerű eredmények formájában. A hosszabb szöveges magyarázat mellőzését kérték a rendezők.
Fizikai állandók és egyéb adatok
Az egyes feladatok szövegében megadott számadatok mellett néhány általános fizikai állandó és egyéb adat ismerete hasznos lehet. Az alábbiakban ilyeneket sorolunk fel. Ezeket általában a lehető legpontosabban adtuk meg, a versenyzőktől azonban azt várjuk el, hogy az eredményeiket a feladat egyéb adatai által indokolt pontossággal adják meg, vagyis minden egyes feladat megoldásakor gondosan ügyeljenek az értékes jegyek számára!
Fénysebesség vákuumban:
A vákuum mágneses permeabilitása:
A vákuum dielektromos állandója:
Gravitációs állandó:
Gázállandó: K)
Boltzmann-állandó: k=1,380658⋅10-23J⋅K-1
Stefan‐Boltzmann-állandó: σ=56,703nW/(m2K4)
A proton töltése: e=1,60217733⋅10-19C
Az elektron tömege: me=9,1093897⋅10-31kg
A Planck-állandó: h=6,6260755⋅10-34J⋅s
A Celsius-skála nullpontja: TK=273,15K
A Nap tömege: MS=1,991⋅1030kg
A Föld tömege: ME=5,979⋅1024kg
A Föld közepes sugara: rE=6,373 Mm
A földpálya nagytengelyének fele: RE=1,4957⋅1011m
Sziderikus nap (csillagnap) hossza: dS=86,16406 ks
Egy év hossza: y=31,558150 Ms
A nehézségi gyorsulás standard értéke a Föld felszínén: g=9,80665m⋅s-2
A légnyomás standard értéke a tengerszinten: p0=101325 Pa
Normál nyomású és 15∘C-os levegő törésmutatója látható fényre: nlev.=1,000277
A napállandó: S=1355W⋅m-2
A Jupiter tömege: M=1,901⋅1027kg
A Jupiter egyenlítői sugara: RB=69,8 Mm
A Jupiter átlagos pályasugara: R=7,783⋅1011m
A Jupiter tengelyforgási ideje: dJ=35,6 ks
A Jupiter keringési ideje: yJ=374,32 Ms
π≈3,14159265
1. feladat. Sugárzás elnyelődése gázban.
Egy hengeres tartály, melynek tengelye függőleges, termikus egyensúlyban lévő gázt tartalmaz. A henger felső felét egy üveglap zárja le, amely dugattyúszerűen szabadon elmozdulhat. Tételezzük fel, hogy nincs gázszivárgás, továbbá az üveglap és a henger fala közötti súrlódás ahhoz elegendő, hogy a dugattyú oszcillációit lecsillapítsa, de egyébként nem okoz számottevő (a többi energiaváltozással összemérhető) energiaveszteséget. Kezdetben a gáz hőmérséklete megegyezik a környezet hőmérsékletével, és a szobában a légnyomás a szokásos érték. A gáz jó közelítéssel ideálisnak tekinthető. Tételezzük fel, hogy a henger oldalai (alap- és fedlapját is beleértve) nagyon rossz hővezetők és kicsiny a hőkapacitásuk. Emiatt a gáz és a környezet közötti hőcsere nagyon lassú, a feladat megoldásakor teljesen elhanyagolható.
Egy állandó teljesítményű lézerrel a felső üveglapon keresztül megvilágítjuk a rendszert. A sugárzás könnyen áthatol a levegőn és az üveglemezen, de az edény belsejében lévő gázban teljesen elnyelődik. A sugárzást elnyelve a gázmolekulák gerjesztett állapotba kerülnek, majd igen gyorsan (több lépésben) infravörös sugárzást kibocsátva visszatérnek alapállapotukba. Ez az infravörös sugárzás azonban a henger falán és az üveglemezen visszaverődik, míg végül a többi molekula teljesen elnyeli. A lézer által leadott energia tehát nagyon rövid idő alatt hőmozgássá (kaotikus molekuláris mozgássá) alakul át, és a továbbiakban elegendően hosszú ideig a gázban marad.
Ha a lézert egy bizonyos ideig működtetjük, azt tapasztaljuk, hogy az üveglap felfelé elmozdul. Ezután kikapcsoljuk a lézert, és megmérjük az üveglap elmozdulását.
| * | a) A feladat végén megadott adatokat (és szükség esetén a fizikai állandókat tartalmazó oldalt is) használva számítsd ki a gáz nyomását és hőmérsékletét a besugárzás után. (2 pont) |
| * | b) Számítsd ki, mennyi mechanikai munkát végez a gáz az elnyelt sugárzás hatására! (1 pont) |
| * | c) Számítsd ki a folyamat során elnyelt sugárzási energiát! (2 pont) |
| * | d) Számítsd ki a lézer sugárzási teljesítményét (vagyis a gáz által elnyelt teljesítményt)! Határozd meg a lézerfényből a gáz által időegységenként elnyelt fotonok (vagyis az elsődleges elnyelődési folyamatok) számát! (1,5 pont) |
| * | e) Számítsd ki, mekkora hatásfokkal alakul át a fényenergia az üveglap mechanikai helyzeti energiájává! (1 pont) |
Döntsük el most lassan a hengert 90 fokkal úgy, hogy a tengelye vízszintes legyen! A gáz és az edény fala közötti hőcserétől most is eltekinthetünk.
| * | f) Megváltozik-e a gáz nyomása és/vagy a hőmérséklete egy ilyen elforgatás során? Ha igen, vajon mennyivel? (2,5 pont) |
Adatok:
A külső légnyomás: p0=101,3 kPa
Szobahőmérséklet: T0=20,0∘C
A henger belső átmérője: 2r=100 mm
Az üveglap tömege: m=800 g
A tartályban lévő gáz mennyisége: n=0,100 mol
A gáz állandó térfogaton mérhető mólhője: CV=20,8 J/(mol⋅K)
A lézerfény hullámhossza: λ=514 nm
A besugárzás ideje: Δt=10,0 s
Az üveglap elmozdulása a besugárzás hatására: Δs=30,0 mm
2. feladat. V-alakú áramvezető mágneses tere.
A mágneses jelenségek Ampre-féle első sikeres leírása idején egy érdekes vita alakult ki az áramjárta vezetők mágneses terének tárgyalásakor, mivel Biot és Savart korai megfontolásai nem egyeztek Ampre eredményével abban az időben.
 6. ábra. 6. ábra.
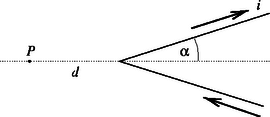
Különösen érdekes esetnek tekinthető, amikor egy hosszú, i árammal átjárt vezetőt két egyenes szakaszra osztunk, melyeket V alakban meghajlítunk úgy, hogy az általuk bezárt szög fele α legyen (lásd az 6. ábrát) Ebben a feladatban α mindvégig radiánban értendő.. Ampre számításai szerint a mágneses indukció vektorának B nagysága egy olyan P pontban, amely a V tengelye mentén, annak külső oldalán a törésponttól d távolságra helyezkedik el, kizárólag úgy függ a szögtől, hogy arányos a tg(α/2) kifejezéssel. Ampre munkája később beépült Maxwell elektromágneses elméletébe, és általánosan elfogadottá vált.
Felhasználva az elektromágnességre vonatkozó mai ismereteinket:
| * | a) Határozd meg a B mágneses indukcióvektor irányát a P pontban. (1 pont) |
| * | b) Tudva, hogy a tér erőssége arányos tg(α/2)-vel, határozd meg a k arányossági tényezőt a |B(P)|=k⋅tg(α/2) összefüggésben. (1,5 pont) |
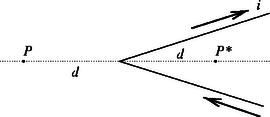
| * | c) Határozd meg a B teret abban a P* pontban, amely P tükörképe a csúcspontra vonatkoztatva, azaz a tengely mentén, a csúcstól ugyancsak d távolságra, de a V belsejében helyezkedik el (lásd a 7. ábrát). (2 pont) |
 7. ábra. 7. ábra.
| * | d) A mágneses tér mérése érdekében a P pontban egy kis mágnestűt helyezünk el, melynek tehetetlenségi nyomatéka I , mágneses momentuma pedig μ. (A lerögzített tengelyű mágnestű egy olyan síkban végez rezgéseket, amely tartalmazza a B irányát.) Számítsd ki, hogy a mágnestű kis rezgéseinek periódusideje hogyan függ B-től! (2,5 pont) |
Ugyanennek a problémának a megoldására Biot és Savart más formulát javasolt. Azt tételezték fel, hogy a P pontban a mágneses indukció (mai jelöléseket használva): ahol μ0 a vákuum mágneses permeabilitása. Ténylegesen elvégzett kísérlettel próbálták eldönteni, hogy a két elmélet közül vajon melyik (Ampre-é vagy Biot és Savart-é) a helyes. Egy mágnestű rezgésidejét mérték a V félnyílásszögének függvényében. Bizonyos α értékeknél azonban a különbség túl kicsi, ezért nem lehet könnyen kimutatni a két elmélet jóslata közötti eltérést.
| * | e) A két elmélet között kísérletileg akkor tudunk különbséget tenni, ha a P pontban lévő mágnestű rezgéseinek T periódusidejére vonatkozó jóslatok legalább 10%-kal eltérnek, vagyis T1>1,1⋅T2. (T1 Ampre jóslata, T2 pedig Biot és Savart-é). Határozd meg, hogyan kell megválasztanunk a V alakú áramjárta vezető α félnyílásszögét ahhoz, hogy a két elmélet között dönthessünk. (3 pont) |
útmutatás: A megoldásod során lehetséges (de az alkalmazott módszertől függően nem szükségszerű), hogy a következő trigonometrikus azonosság hasznosnak bizonyul számodra: tg(α/2)=sinα/(1+cosα).
3. feladat. Űrszonda a Jupiter gravitációs terében.
Ebben a feladatban egy olyan módszerrel (a ,,gravitációs parittyával'') foglalkozunk, melyet gyakran használnak űrszondák gyorsítására Lásd még a Csillagászat rovat újdonságai között a Cassini-űrszondáról szóló ismertetést.. Az űrszonda megközelít egy bolygót, majd a bolygó hatására a szonda sebessége jelentősen megnövekedhet, mozgásiránya lényegesen megváltozhat, és eközben a bolygó pályamenti mozgásához tartozó energia igen csekély mértékben lecsökken. A továbbiakban ezt a hatást fogjuk tanulmányozni egy a Jupiter közelében elhaladó űrszondánál.
A Jupiter bolygó olyan ellipszispályán kering a Nap körül, amely az átlagos R sugárnak megfelelő körpályával közelíthető. Mielőtt a fizikai folyamatok elemzésébe kezdenénk, válaszolj a következő egyszerű kérdésekre:
| * | a) Mekkora V sebességgel kering a Jupiter a Nap körül? (1,5 pont) |
| * | b) Amikor a szonda a Nap és a Jupiter között (azokat összekető egyenes mentén) van, a Jupitertől milyen távolságra található az a pont, ahol a Nap gravitációs vonzása kiegyenlíti a Jupiterét? (1 pont) |
Egy m=825 kg tömegű űrszonda repül a Jupiter felé. Az egyszerűség kedvéért tegyük fel, hogy a szonda pályája éppen a Jupiter pályasíkjában fekszik. (Ezáltal nem vesszük figyelembe azt a fontos lehetőséget, hogy a szonda a Jupiter pályasíkjából kilökődhet.)
Csak azzal foglalkozzunk, mi történik abban a tartományban, ahol a Jupiter vonzása felülmúl minden más gravitációs erőt.
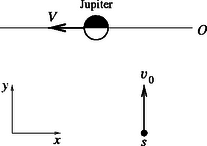 8. ábra. A Jupiter pályája (O) és az űrszonda pályája (s) a Nap tömegközéppontjához rögzített vonatkoztatási rendszerben. 8. ábra. A Jupiter pályája (O) és az űrszonda pályája (s) a Nap tömegközéppontjához rögzített vonatkoztatási rendszerben.
A Nap tömegközéppontjához rögzített vonatkoztatási rendszerben a szonda kezdeti sebessége v0=1,00⋅104 m/s (a pozitív y tengely irányában), míg a Jupiter sebessége negatív x irányú (lásd az 8. ábrát). A ,,kezdeti sebesség'' a szondának azt a sebességét jelenti, amikor még a bolygóközi térben, a Jupitertől messze van, de már abban a tartományban, ahol a Nap vonzása elhanyagolható a Jupiteré mellett. Feltesszük, hogy a bolygóval történő találkozás olyan rövid idő alatt zajlik le, hogy a Jupiter Nap körüli pályamozgásában bekövetkező irányváltozást elhanyagolhatjuk. Azt is feltesszük, hogy a szonda a Jupiter mögött halad el, vagyis a szonda x koordinátája nagyobb, mint a Jupiteré, amikor az y koordináták megegyeznek.
| * | c)Add meg az űrszonda mozgásirányát (a sebességvektor és az x tengely által bezárt φ szöget), továbbá a szonda v' sebességét a Jupiter vonatkoztatási rendszerében, ha a szonda messze van a Jupitertől. (2 pont) |
| * | d)Határozd meg a szonda teljes E mechanikai energiáját a Jupiter vonatkoztatási rendszerében, amikor a szonda még elegendően messze van ahhoz, hogy a gravitációs kölcsönhatás gyengesége miatt csaknem egyenletes sebességgel mozogjon. (A potenciális energiát ‐ szokásos módon ‐ nagyon nagy távolságban választjuk nullának.) (1 pont) |
Az űrszonda pályája a Jupiter vonatkoztatási rendszerében egy hiperbola, melynek polárkoordinátákkal kifejezett egyenlete ebben a vonatkoztatási rendszerben: | 1r=GMv'2b2(1+1+2Ev'2b2G2M2mcosθ), | (1) |
ahol b az egyik aszimptota távolsága a Jupitertől (az úgynevezett impakt paraméter), E a szonda teljes mechanikai energiája a Jupiter vonatkoztatási rendszerében, G a gravitációs állandó, M a Jupiter tömege, r és θ polárkoordináták (a vezérsugár és a polárszög).
A 9. ábra az (1) egyenlet által leírt hiperbola két ágát ábrázolja (az aszimptotákat és a polárkoordinátákat is feltüntetve). ügyelj arra, hogy az (1) egyenletbeli origó a hiperbola ,,vonzó fókuszpontja''. A szonda pályagörbéje a vonzási pálya, melyet a 9. ábrán folytonos vonal jelöl.
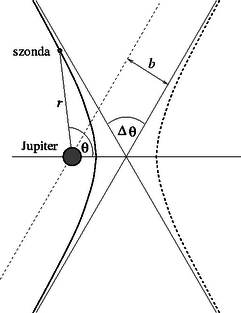 9. ábra. 9. ábra.
| * | e)Felhasználva a pályagörbét leíró (1) egyenletet, határozd meg a teljes Δθ szögeltérülést a Jupiter vonatkoztatási rendszerében (lásd a 9. ábrát), és fejezd ki ezt a szögeltérülést a kezdeti v' sebesség, valamint a b impakt paraméter függvényében! (2 pont) |
| * | f)Tételezzük fel, hogy a szonda nem kerülhet közelebb a Jupiter középpontjához, mint a bolygó (a Jupiter) sugarának háromszorosa. Számítsd ki ebben az esetben a legkisebb impakt paramétert és az így létrejövő legnagyobb szögeltérülést! (1 pont) |
| * | g)Vezess le egy olyan egyenletet, amely megadja a Nap vonatkoztatási rendszerében a szonda v'' végsebességét a Jupiter V sebességének, a szonda kezdeti v0 sebességének és a Δθ szögeltérülésnek a függvényében! (1 pont) |
| * | h) A fenti eredmények felhasználásával add meg numerikusan a szonda v'' végsebességét a Nap vonatkoztatási rendszerében, ha a szögeltérülés a lehető legnagyobb megengedett értékű! (0,5 pont) |
12345678 |
 PDF | MathML
PDF | MathML 







