Cím:	Az 1997/98. tanévben megrendezett fizika OKTV II. fordulójának feladatmegoldásai
Szerző(k):	Holics László
Füzet:	1999/január, 44 - 53. oldal	PDF  |  MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.     A fizika I. kategória (szakközépiskolások) feladatai       1. feladat. Rakéta modellünk egy kiskocsi, amelyen több rugós kilövő szerkezet van elhelyezve. Mindegyik rugó meg van feszítve, és így $E=100\text{J}$ rugalmas energiát tárol. A $M=100\text{kg}$ össztömegű rendszer kezdetben nyugalomban van. Mekkora lesz a kiskocsi sebessége, ha egymás után három, egyenként $m=5\text{kg}$ tömegű golyót lő ki a szerkezet a kocsi hossztengelye mentén ugyanabba az irányba?  (Arany Tóth László)    Megoldás. Válasszuk vonatkoztatási rendszerül mindig a kocsi kidobás előtti sebességével haladó (tömegközépponti) vonatkoztatási rendszert! Legyen a kocsi sebessége az első kilövés után $V_1$, a golyó sebessége pedig $v_1$! A mechanikai energia és a lendület megmaradása miatt $\begin{array}{c}{\displaystyle E=\frac{1}{2}\left(M-m\right)V_1^2+\frac{1}{2}m{v}_1^2\mathrm{,}\left(M-m\right)V_1-m{v}_1=\mathrm{0,}}\end{array}$ ahonnan a kiskocsi sebessége (sebességváltozása) az első kilövés után $\begin{array}{c}{\displaystyle V_1=\Delta V_1=\sqrt[]{\frac{2mE}{M\left(M-m\right)}}\mathrm{.}}\end{array}$ A második kilövés után a kocsi sebességváltozása pontosan a fenti képlet szerint számítható, azzal a különbséggel, hogy most $M$ helyett $M\text{'}=M-m$ szerepel: $\begin{array}{c}{\displaystyle \Delta V_2=\sqrt[]{\frac{2mE}{\left(M-m\right)\left(M-2m\right)}}\mathrm{,}}\end{array}$ a harmadik kilövés után pedig $M$ helyett $M\text{'}\text{'}=M-2m$ írandó: $\begin{array}{c}{\displaystyle \Delta V_3=\sqrt[]{\frac{2mE}{\left(M-2m\right)\left(M-3m\right)}}\mathrm{.}}\end{array}$ A kiskocsi teljes sebességváltozása (a talajhoz viszonyított sebessége) három golyó kilövése után: $\begin{array}{c}{\displaystyle V_3=\Delta V_1+\Delta V_2+\Delta V_3=1\mathrm{,}03\text{m/s}\mathrm{.}}\end{array}$   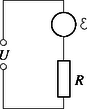2. feladat. Egyenáramú villanymotorunk álló- és forgórész tekercse sorba van kapcsolva, s összesen $62\Omega$ ellenállása van. A motort $220\text{V}$ egyenfeszültségre kapcsoljuk. Leadhat-e ez a motor $200\text{W}$ mechanikai teljesítményt?  (Légrádi Imre)    Megoldás. A kapcsolás vázlata az 1. ábrán látható. Ha a motor forog, az armatúra vezetőiben az állórész mágneses mezeje elektromotoros erőt indukál. Jelölje a forgórészben mint generátorban keletkezett feszültséget $\text{E}$, az ohmikus ellenállásra eső feszültség pedig $IR\mathrm{.}$ Kirchhoff törvénye szerint: $U-\text{E}-IR=\mathrm{0,}$ ebből $\text{E}=U-IR$ a motor feszültsége, amely a mechanikai teljesítmény szempontjából számít. A motor teljesítménye: $\begin{array}{c}{\displaystyle P=I\text{E}=I\left(U-IR\right)=-R{\left(I-\frac{U}{2R}\right)}^2+\frac{U^2}{4R}\le \frac{U^2}{4R}=P_{\text{max}}=195\mathrm{,}16\text{W}\mathrm{.}}\end{array}$ A motor tehát nem tud leadni $200\text{W}$ mechanikai teljesítményt.   3. 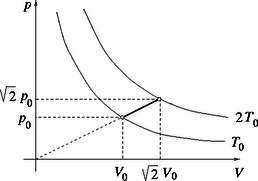feladat. $1$ mól kétatomos gázzal a 2. ábrán látható körfolyamatot hajtunk végre. A gáz által felvett hőnek hány százaléka fordítódik hasznos munkára?  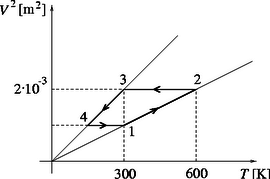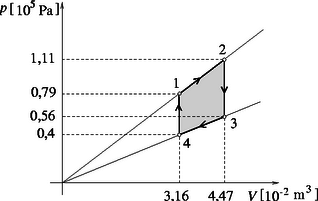(Jurisits József)    Megoldás. Az $1\to 2$ és $3\to 4$ folyamatokban $T\propto V^2\mathrm{,}$ ahonnan a gáztörvény felhasználásával adódik, hogy $p\propto \left(T/V\right)\propto V\mathrm{.}$ A körfolyamat tehát a $p-V$ diagramon is egy trapézzal szemléltethető, és az 1., 2., 3. és 4. pontok állapotjelzői a megadott adatokból, illetve a gáztörvényből kiszámítható (3. ábra). A hasznos munka: $\begin{array}{c}{\displaystyle W=\frac{p_1+p_2}{2}\left(V_2-V_1\right)-\frac{p_3+p_4}{2}\left(V_2-V_1\right)=615\mathrm{,}7\text{J}\mathrm{.}}\end{array}$ A felvett hő: $\begin{array}{c}{\displaystyle Q_{\text{fel}}=Q_{41}+Q_{12}=\Delta E_{41}+\Delta E_{12}-W_{12}=\frac{f}{2}nR\left(T_2-T_4\right)+\frac{p_1+p_2}{2}\left(V_2-V_1\right)=10\mathrm{,}6\text{kJ, }}\end{array}$ A hatásfok: $\eta =W/Q=5\mathrm{,}81\%$.   4. feladat. Egy fotocella katódját növekvő frekvenciájú fénnyel megvilágítva $3\cdot {10}^{14}{\text{s}}^{-1}$ frekvencia esetén indul meg az anódáram. Ezen fotocella anódja és katódja közé $1\text{pF}$ kapacitású kondenzátort kapcsolunk, és a katódot $425\text{nm}$ hullámhosszú fénnyel világítjuk meg. Elegendő hosszú ideig történt megvilágítás esetén hány elektron érkezik az anódra?  (Blészer Jenő)    Megoldás. Az anódáram megindulásakor a foton energiája a kilépési munkát fedezi: $W_{\text{ki}}=h{f}_1=2\cdot {10}^{-19}\text{J}\mathrm{.}$ A második esetben alkalmazott fény frekvenciája: $f_2=c/\lambda =7\cdot {10}^{14}{\text{s}}^{-1}\mathrm{.}$ A katódot elhagyó elektronok mozgási energiája: $E_{\text{m}}=h{f}_2-W_{\text{ki}}=2\mathrm{,}64\cdot {10}^{-19}\text{J}\mathrm{.}$ Miközben az elektronok a katódból kilépve az anódra jutnak, a katód pozitív, az anód negatív töltésűvé válik, és ezáltal egy ,,ellentér" alakul ki, amely elegendően hosszú idő múlva leállítja az elektronok anódra jutását. A kondenzátoron kialakult $U$ ellenfeszültség mérhető a katód és az anód között is. Ez az elektromos mező az elektronok potenciális energiájának felemelésére elektrononként $eU$ munkát végez, ami a munkatétel szerint $\left(W=\Delta E_{\text{kin}}\right)$ megegyezik az elektron mozgási energiájának megváltozásával: $eU=0-E_{\text{m}}$, ahonnan kiszámítható a katódnak az anódhoz viszonyított feszültsége: $U=1\mathrm{,}65\text{V}$. A kondenzátor töltése: $Q=CU=1\mathrm{,}65\cdot {10}^{-12}\text{C}$, a kondenzátorra jutó elektronok száma: $n=Q/e=1\mathrm{,}03\cdot {10}^7$ db. (A fotocella saját kapacitását elhanyagoltuk.)     A fizika II. 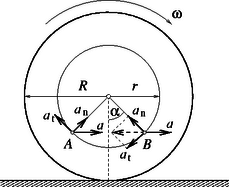kategória feladatai       1. feladat. Autó kerekének sugara $R$. A szelepsapka $r$ távolságra van a kerék tengelyétől. Az autó álló helyzetből csúszásmentesen, állandó gyorsulással elindul. Megvalósítható-e valamilyen módon, hogy a szelepsapkának ne legyen gyorsulása a) az alsó helyzet utáni $1/8$ fordulatnál, b) az alsó helyzet előtti $1/8$ fordulatnál?  (Jurisits József)    I. megoldás. A kívánt gyorsulásmentes állapothoz az adott pillanatban az autó (keréktengely) gyorsulásának $\left(\text{a}\right)$, a szelepsapka sugár irányú (normál) gyorsulásának $\left({\text{a}}_n\right)$ és érintőleges (tangenciális) gyorsulásának $\left({\text{a}}_t\right)$ zérus eredőt kell adnia. A 4. ábrából látszik, hogy az $a)$ esetnek megfelelő $A$ pontban ez nem teljesülhet. A b) esetben ($B$ pontban) fennállhat a kért gyorsulásmentesség, ha a tangenciális és normális gyorsulás egyenlő nagy, és a belőlük alkotott vektorparalelogramma olyan négyzet, amelynek az átlója éppen az autó gyorsulásával azonos nagyságú: $a_t=a_n=a/\sqrt[]{2}\mathrm{,}$ azaz $a/\sqrt[]{2}=r\left(a/R\right)$, ahonnan $R=r\sqrt[]{2}\mathrm{.}$ Eszerint a szelepsapka csak meghatározott távolságra $\left(r=R/\sqrt[]{2}\approx 0\mathrm{,}71R\right)$ lehet a tengelytől. Mivel az indulás után $t$ idővel $a_n=r{\left(at/R\right)}^2$ és $a_t=r\left(a/R\right)\mathrm{,}$ az $a_t=a_n$ feltétel akkor teljesül, ha $t=\sqrt[]{R/a}$, és így a kerék szögelfordulása az indulási helyzethez képest $\begin{array}{c}{\displaystyle \phi =\beta \frac{t^2}{2}=\frac{1}{2}\frac{a}{R}{t}^2=\frac{1}{2}\text{rad}=28\mathrm{,}{65}^{\circ }\mathrm{.}}\end{array}$ Eszerint az indulás pillanatában a szelepsapkához húzott sugár a függőlegessel $\alpha +\phi =73\mathrm{,}{65}^{\circ }$-os szöget kell bezárjon.   2. feladat. Egy $f$ szabadsági fokú ideális gáz $T_0$ hőmérséklettől $2T_0$-ig tartó folyamata esetén $V=a{T}^2$ $(a=$ konstans). Adjuk meg a mólhőt a hőmérséklet függvényében!  (Szvetnik Endre)    Megoldás. A hőtan első főtétele $\left(\Delta E=Q+W\right)$ kis megváltozásokra (amikor a nyomás állandónak vehető): $\begin{array}{c}{\displaystyle n{C}_V\Delta T=nC\Delta T-p\Delta V\mathrm{.}}\end{array}$ Innen kifejezhetjük a $T$ hőmérséklethez tartozó mólhőt: $\begin{array}{c}{\displaystyle C\left(T\right)=C_V+\frac{1}{n}p\left(T\right)\cdot \frac{\Delta V\left(T\right)}{\Delta T}\mathrm{.}}\end{array}$ Felhasználhatjuk, hogy pl. a szabadesésnél $g{t}^2/2$ változási gyorsasága $gt$, így az $a{T}^2$ függvény ($T$ változó szerinti) változási üteme $2aT$. Eszerint $\begin{array}{c}{\displaystyle C\left(T\right)=C_V+\frac{1}{n}p\left(T\right)\cdot 2aT\mathrm{.}}\end{array}$ A nyomást az ideális gáz állapotegyenletéből kifejezve és $V=a{T}^2$ -et felhasználva végül azt kapjuk, hogy a folyamat során mólhő állandó, értéke $C=C_V+2R=\left(f/2\right)R+2R$.   3. feladat. Egy $l$ hosszúságú, $N$ menetes nyitott szolenoid felénél, belül lévő $r$ sugarú körgyűrűben az áramerősség időben egyenletesen változik. A körgyűrű síkja merőleges a szolenoid tengelyére, az áramerősség változási gyorsasága $\Delta I/\Delta t\mathrm{.}$ a) Mekkora feszültség indukálódik a szolenoidban? (Adatok: $l=2\text{m}\mathrm{,}$ $N=2000$, $r=5\text{cm}\mathrm{,}$ $\Delta I/\Delta t=40\text{A}/\text{s}$, $L_{12}=L_{21}$.) b) A fenti elrendezésnél a tekercs árama állandó $I_2$ nagyságú, a körgyűrű árama pedig kezdeti zérus értékről egyenletesen $I_1$-re nő. A körgyűrű önindukciós együtthatója $L_1$. Mennyivel változik a mágneses mező energiája a folyamat során? (Adatok: $I_1=2\text{A}$, $I_2=4\text{A}$, $L_1=0\mathrm{,}3\mu \text{H}$.)  (Szvetnik Endre)    Megoldás. $a)$ A szolenoid feszültsége: $U_2=L_{21}\left(\Delta I/\Delta t\right)$ módon számítható; feladatunk tehát $L_{21}$, vagy a vele megegyező $L_{12}$ kölcsönös indukciós együttható meghatározása. Tekintsük azt az elrendezést, amikor a körgyűrű nyitott, és a szolenoidon átfolyó áram tetszőleges $\Delta I_2/\Delta t$ tempóban változik! Ekkor a körgyűrű feszültsége a kölcsönös indukciós együtthatóval és a Faraday-féle indukciós törvénnyel felírva: $\begin{array}{c}{\displaystyle U_1=L_{12}\frac{\Delta I_2}{\Delta t}=\frac{\Delta \Phi }{\Delta t}=\frac{{\mu }_{0}N{r}^2\pi }{l}\frac{\Delta I_2}{\Delta t}\mathrm{,}}\end{array}$ ahonnan $L_{12}={\mu }_{0}N{r}^2\pi /l\mathrm{,}$ és szolenoidban indukálódó feszültség $U_2\approx 0\mathrm{,}4\text{mV}\mathrm{.}$ $b)$ Határozzuk meg először a körgyűrű telepének a Joule-féle hőn felüli energiaváltozását! A szolenoid által keltett mágneses mező (állandó lévén) nem hoz létre fluxusváltozást a körgyűrűben, így a keresett energia úgy számítható, mintha a szolenoid nem lenne jelen. A körgyűrű telepének energiája tehát a mágneses mező keltése miatt $\Delta W_1=-L_1{I}_1^2/2$ értékkel megváltozott (lecsökkent). Mivel a körgyűrű változó árama fluxusváltozást hoz létre a szolenoidban, így annak állandó árama egy megfelelő telep működtetésével biztosítható. Keressük meg ennek a telepnek a fluxusváltozás miatti energiaváltozását: $\begin{array}{c}{\displaystyle \Delta W_2=\mp U_2{I}_{2}t=\mp L_{12}\cdot \left(I_1/t\right)\cdot I_{2}t=\mp L_{12}\cdot I_1{I}_2\mathrm{.}}\end{array}$ (Az előjel attól függően pozitív vagy negatív, hogy a köráram és a szolenoidban folyó áram azonos vagy ellentétes irányú.) A két telep együttes energiaváltozásának $\left(-1\right)$-szerese természetesen egyenlő a mágneses mező energiaváltozásával (a Joule-féle hőhöz szükséges energiaváltozástól eltekintve, amit itt nem is számítottunk bele.) Ezzel a mágneses mező keresett energiaváltozása: $\begin{array}{c}{\displaystyle \Delta W_m=-\left(\Delta W_1+\Delta W_2\right)=\frac{1}{2}{L}_1{I}_1^2\pm L_{12}{I}_1{I}_2=\left(0\mathrm{,}6\pm 79\right)\cdot {10}^{-6}\text{J}\mathrm{.}}\end{array}$   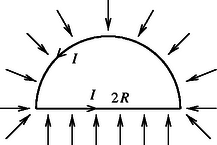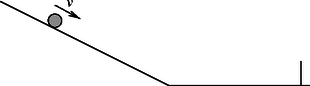4. feladat. Magas lejtőről csúszásmentesen gurul le egy golyó a törésmentesen csatlakozó vízszintes síkra. A golyó útjában egy fal áll. Melyik esetben ér előbb a pálya végén levő falhoz, ha van a vízszintes síkon súrlódás, vagy ha nincs? Adja meg és indokolja a válaszát arra az esetre, ha a folyamat a) levegőben, illetve b) vákuumban megy végbe!  (Holics László)    Megoldás. $a)$ A leguruló golyó a hosszú lejtőn viszonylag nagy sebességre tesz szert, tehát a közegellenállás jelentős. A két eset összehasonlításában csak ez okozhat különbséget. A golyó mindkét esetben azonos végsebességgel érkezik a lejtő aljára. Ha nincs súrlódás a vízszintes síkon, akkor csak a közegellenállás fékezi a golyót, és az valamennyire csökkenő sebességgel valamennyi idő alatt eléri a falat, miközben változatlan szögsebességgel forog. 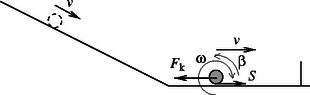Ha van súrlódás a vízszintes síkon, akkor a tömegközéppontot fékező közegellenállás tapadó súrlódási erőt provokál ki a talajból (u.i. a csúszásmentesség kezdeti $a=r\beta$ kényszerkapcsolata mindvégig megmarad), és ez a kényszerkapcsolat a szögsebességgel ellentétes irányú (fékező) szöggyorsulást kell hogy eredményezzen. Így a forgási energia egy része áttevődik a haladási szabadsági fokra, illetve a haladás irányába előremutató $S$ tapadó súrlódási erő segíti a golyót a haladásában (6. ábra). Lassabban csökken a tömegközéppont sebessége, és így előbb éri el a falat. $b)$ Ha nincs közegellenállás, a gördülő golyó lényegében mindkét (súrlódásos és súrlódásmentes) esetben azonos idő alatt éri el a falat, mivel hiányzik a tömegközéppont sebességét csökkentő erőhatás. A golyó tehát mindkét esetben csúszásmentesen gördül, még a tapadási erő hiányában is. Ha azonban figyelembe vesszük ─ az egyébként rendszerint elhanyagolható ─ gördülő ellenállást, a súrlódásos esetben ér egy hajszálnyival később ér a falhoz a golyó, ui. a gördülő ellenállás a talaj benyomódásának következménye (feltehetjük, hogy sima és érdes talajon azonos érték), és mint ilyen fékező forgatónyomatékot fejt ki a golyóra, azaz most a tömegközéppont gyorsabban halad, mint a sugár és szögsebesség szorzata, így a talajra előre mutató súrlódási erőt fejt ki. Ennek az erőnek az ellentettje hat a golyóra, tehát kis mértékben fékezi azt, míg a súrlódásmentes talajon ez az erő nem lép fel.     A fizika III. 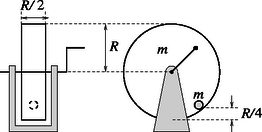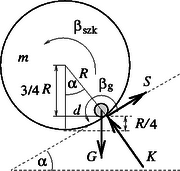kategória feladatai       1. feladat. Egy könnyen forgatható $m$ tömegű szerencsekerék $R$ sugarú, $R/2$ magasságú hengerének alapja és palástja azonos vastagságú és anyagú lemezből készült. A kezdetben nyugvó kerék belsejében $r=R/6$ sugarú, ugyancsak $m$ tömegű tömör golyó a henger aljától $R/4$ magasságban érintkezik a henger felületével, és a kezdőpillanatban nyugalomban van. a) Mekkora forgatónyomatékot kell a szerencsekerékre kifejtenünk, hogy a benne levő gömb tömegközéppontja nyugalomban maradjon? b) Mekkora munkát végzünk így $2\text{s}$ alatt? c) Mekkora a golyó és a szerencsekerék szöggyorsulása? (A golyó csúszásmentesen gördül. Legyen $R=\mathrm{0,54}\text{m}$ és $m=2\text{kg}$. A hajtókar tömege elhanyagolható.)  (Holics László)    Megoldás. $a)$ Ahhoz, hogy a golyó tömegközéppontja helyben maradjon, a rá ható összes erők összege zérus kell hogy legyen. A golyóra a nehézségi erő, a kényszererő és a tapadó súrlódási erő hat (8. ábra). A tapadási erő $S=mg\text{sin}\alpha$ kell legyen (hiszen a golyó érintő irányban nem gyorsul). A megadott feltétel szerint $\text{sin}\alpha =d/R=\sqrt[]{7}/\mathrm{4,}$ innen $\alpha =41\mathrm{,}{4}^{\circ }\mathrm{,}$ a tapadási súrlódási erő pedig $13\mathrm{,}23\text{N}$. A golyó kerületi gyorsulása $\begin{array}{c}{\displaystyle a_k=r{\beta }_{\text{golyó}}=r\frac{Sr}{\frac{2}{5}m{r}^2}=\frac{5g\text{sin}\alpha }{2}\mathrm{.}}\end{array}$ (Természetesen ugyanekkora a szerencsekerék palástjának kerületi gyorsulását is.) A szerencsekerék szöggyorsulása: ${\beta }_{\text{szk}}=a_k/R\mathrm{.}$ Ezt a kerékre ható forgatónyomatékok, vagyis az általunk kifejtett $M$ forgatónyomaték és a tapadó súrlódási erő $SR$ forgatónyomatékának különbsége okozza: $M-SR={\Theta }_{\text{szk}}{\beta }_{\text{szk}}\mathrm{.}$ Meghatározandó még a szerencsekerék tehetetlenségi nyomatéka. Mivel (a megadott adatok mellett) a palást területe éppen megegyezik egy-egy körlap területével, a tömegek aránya is ennek megfelelő: $m_{\text{palást}}=\frac{1}{3}m\mathrm{,}$ illetve $m_{\text{alap}}=\frac{2}{3}m\mathrm{.}$ Így $\begin{array}{c}{\displaystyle {\Theta }_{\text{szk}}={\Theta }_{\text{palást}}+{\Theta }_{\text{alap}}=m_{\text{palást}}\cdot R^2+m_{\text{alap}}\cdot \frac{R^2}{2}=\frac{m}{3}\cdot R^2+\frac{2m}{3}\cdot \frac{R^2}{2}=\frac{2}{3}m{R}^2\mathrm{.}}\end{array}$ Az általunk kifejtendő forgatónyomaték tehát $M=\frac{8}{3}mgR\text{sin}\alpha \approx 19\mathrm{,}1\text{Nm}\mathrm{.}$ $b)$ Munkavégzésünk a kerék és a golyó mozgási energiáját növeli: $\begin{array}{c}{\displaystyle W=\Delta E_{\text{szk}}+\Delta E_{\text{golyó}}=\frac{1}{2}{\Theta }_{\text{szk}}{\omega }_{\text{szk}}^2+\frac{1}{2}{\Theta }_{\text{golyó}}{\omega }_{\text{golyó}}^2=\frac{8}{15}m{R}^2{\left({\beta }_{\text{szk}}t\right)}^2=1\mathrm{,}17\text{kJ}\mathrm{.}}\end{array}$ $c)$ A szerencsekerék szöggyorsulása ${\beta }_{\text{szk}}=a_{\text{szk}}/R\approx 30\mathrm{,}6{\text{s}}^{-2}$, a golyóé pedig ${\beta }_{\text{golyó}}=6{\beta }_{\text{szk}}\approx 184{\text{s}}^{-2}$.   2. feladat. 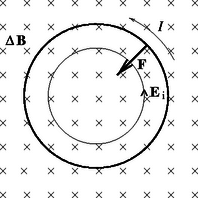$R=8\text{cm}$ sugarú, $A=2{\text{mm}}^2$ kör keresztmetszetű rézkarika egyenletesen változó indukciójú, a síkjára merőleges homogén mágneses mezőben van. Az indukció $t=0$-kor $B_0=0$, és $t=0\mathrm{,}2\text{s}$ alatt $B=2\text{T}$ értékre nő. Mekkora $\omega$ szögsebességgel kell a karikát egyenletesen forgatnunk, hogy $t_1=0\mathrm{,}1\text{s}$ időpillanatban ne legyen benne rugalmas feszültség? Megoldható-e ez a feladat $2\text{T}$-ról $0$-ra csökkenő mágneses indukció esetén? (Az önindukciós hatás elhanyagolható.)  (Holics László)    I. megoldás Az időben változó mágneses mező elektromos mezőt kelt, amely a fémgyűrűbe hatol és abban áramot indít meg. Erre az immár áramtól átjárt vezetőre ugyanettől (az időben növekvő indukciójú) mezőtől az indukcióvonalakra és a körvezetőre merőleges, az indukált áram iránya miatt a kör középpontja felé irányuló Lorentz-erő hat (9. ábra), amely a körvezetőt összeroppantani igyekszik. Ezáltal abban rugalmas feszültséget hoz létre. (Ha időben csökkenő indukciójú mágneses mezőben lenne a karika, akkor arra szétfeszítő erő hatna!) Meg kell határoznunk ezt az erőt. Mivel a mező időben egyenletesen változik, az indukált elektromos térerősség és így a körfeszültség is időben állandó, az önindukció nem játszik szerepet. Az indukált áram erőssége (Ohm törvényét alkalmazva esetünkre): $\begin{array}{c}{\displaystyle I=\frac{U_0}{r}=\frac{\Delta \Phi }{r\Delta t}=\frac{\Delta B{R}^2\pi }{\left(2R\pi \varrho /A\right)\Delta t}=\frac{\Delta B}{\Delta t}\cdot \frac{RA}{2\varrho }\mathrm{.}}\end{array}$ A keletkező rugalmas feszültséget úgy számíthatjuk ki legegyszerűbben, hogy meghatározzuk az egy félkörre ható eredő mágneses erőt, és azt osztjuk a vezeték keresztmetszetének kétszeresével. A félkörre ható erő pedig nyilván akkora, mint egy félkörből és átmérőjéből álló áramjárta vezeték $2R$ átmérőjére ható erő, hiszen a vezető a homogén mezőben semerre sem gyorsul, így a rá ható Lorentz-erő eredője nulla kell legyen (10. ábra). Ezzel a félkörre ható erő: $F=B_{1}I\cdot 2R\mathrm{,}$ ahol $B_1$ a $t_1$ időpillanatban a mágneses indukció nagysága. Mivel a félkör végpontjaiban az egyik félkört a másikkal összenyomó erők egymással párhuzamosak, az egyik keresztmetszetre az eredő fele jut: $F_1=F/2=B_{1}IR$, ahol $B_1=\left(\Delta B/\Delta t\right)t_1=B_{\text{max}}/2.$ Így a rugalmas feszültség, amit a Lorentz-erő okoz: $\begin{array}{c}{\displaystyle \sigma =\frac{F_1}{A}=\frac{1}{A}\frac{B_{\text{max}}}{2}\frac{\Delta B}{\Delta t}\frac{RA}{2\varrho }R=\frac{B_{\text{max}}}{4\varrho }{R}^2\cdot \frac{\Delta B}{\Delta t}\mathrm{.}}\end{array}$ A karika megforgatásával azt érjük el, hogy a mágneses mező okozta nyomófeszültség mellett egy húzófeszültség is fellép, amelyek ─ megfelelő fordulatszám esetén ─ éppen kompenzálhatják egymást. Ezért nem sikerülne a kísérlet csökkenő indukciójú mezőben, ahol a mágneses erők is széthúzó jellegűek (a karikában az áram iránya ellentétesre változna, de a $\text{B}$ vektor iránya ugyanaz maradna, s így a Lorentz-erő iránya megfordulna). 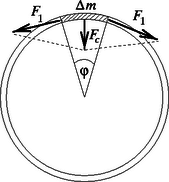A mechanikai feszültség kétféle gondolatmenettel is meghatározható. A középpontján átmenő, síkjára merőleges tengely körül megforgatott gyűrű kicsiny, $d$ sűrűségű, $\Delta m=dAR\phi$ tömegű darabjára $\begin{array}{c}{\displaystyle F_c=\Delta m\cdot R{\omega }^2=A{R}^{2}d\cdot \phi \cdot {\omega }^2}\end{array}$ nagyságú centripetális erőnek kell hatnia, ha a kis tömegelemet egyenletes körmozgásra kényszerítjük. Ezt az erőt a vele érintkező szomszédos rétegek fejtik ki (rugalmas kölcsönhatás útján) a 11. ábrának megfelelően. A $\phi$ középponti szög a kétfelé húzó erővektorok által bezárt szöggel is egyenlő (merőleges szárú szögek), ezért az erők eredője (a tömegelemre ható centripetális erő): $\begin{array}{c}{\displaystyle F_c=2F_1\text{sin}\frac{\phi }{2}\approx 2F_1\frac{\phi }{2}\mathrm{.}}\end{array}$ $F_c$ kétféleképpenm felírt alakjának összevetéséből a húzóerőre $F_1=A{R}^2{\omega }^{2}d$, a rugalmas feszültségre pedig ${\sigma }_r=F_1/A=R^2{\omega }^{2}d$ adódik. A két különböző okból keletkező, ellenkező irányú rugalmas feszültség megkívánt egyenlőségéből meghatározhatjuk a szükséges szögsebességet: $\begin{array}{c}{\displaystyle \omega =\frac{1}{2}\sqrt[]{\frac{B_{\text{max}}}{\varrho d}\frac{\Delta B}{\Delta t}}\approx 177{\text{s}}^{-1}\mathrm{,}}\end{array}$ illetve a megfelelő fordulatszámot: $n=\omega /\left(2\pi \right)=28\mathrm{,}2{\text{s}}^{-1}\mathrm{.}$   II. megoldás. Abból is kiindulhatunk, hogy akkor nem keletkezik rugalmas feszültség a karikában, ha annak egy tetszőleges kis tömegelemére ható mágneses Lorentz-erő éppen az $R$ sugarú körpályához tartozó normálerőt biztosítja (ekkor ui. akár egymástól mechanikailag független körívdarabkákra oszthatnánk a karikát, részei megmaradnának az $R$ sugarú pályán, a karika alakja nem változna meg rugalmas feszültség hiányában sem). A rézkarika kicsiny $\Delta l$ hosszúságú, $\Delta m$ tömegű darabkájának mozgásegyenlete (csak sugár irányú erő hat): $B\cdot i\cdot \Delta l=\Delta mR{\omega }^2\mathrm{.}$ $\Delta l$-lel osztva a lineáris tömegsűrűség jelenik meg, ami az össztömegből és a kerületből kiszámítható: $\begin{array}{c}{\displaystyle B\cdot i=\frac{\Delta m}{\Delta l}R{\omega }^2=\frac{m}{2R\pi }R{\omega }^2=\frac{m{\omega }^2}{2\pi }\mathrm{.}}\end{array}$ A pillanatnyi indukció és a pillanatnyi áramerősség értékét beírva: $\begin{array}{c}{\displaystyle \frac{\Delta B}{\Delta t}t\cdot \frac{U_{\text{ind}}}{r}=\frac{m{\omega }^2}{2\pi }\mathrm{.}}\end{array}$ Az indukált feszültség és a körvezető ellenállása az adatokból meghatározható, a karika tömege pedig a sűrűségével és a geometriai adataival kifejezhető. Ezeket is felhasználva mozgásegyenletünk így írható: $\begin{array}{c}{\displaystyle {\left(\frac{\Delta B}{\Delta t}\right)}^2\cdot t\cdot \frac{RA}{2\varrho }=RA{\omega }^{2}d\mathrm{,}}\end{array}$ ahonnan a keresett szögsebesség (a karika sugarától és vastagságától függetlenül) $\begin{array}{c}{\displaystyle \omega =\frac{\Delta B}{\Delta t}\sqrt[]{\frac{t}{2\varrho d}}\approx 177{\text{s}}^{-1}\mathrm{.}}\end{array}$   3. feladat. $T_0=300\text{K}$ hőmérsékletű héliumgáz $2T_0$-ig tartó folyamatában a mólhő $2R=$ állandó. A folyamatban szereplő gáz anyagmennyisége $n=5$ mol, a $T_0$-hoz tartozó térfogat $V_0=0\mathrm{,}2{\text{m}}^3$. Ábrázoljuk a folyamat $p-V$ diagramját!  (Szvetnik Endre)    Megoldás. A hőtan első főtétele kis megváltozásokra egyatomos gáz esetén: $\begin{array}{c}{\displaystyle \frac{3}{2}Rn\Delta T=2Rn\Delta T-p\Delta V\mathrm{,}\text{vagyis}2p\Delta V=nR\Delta T\mathrm{.}}\end{array}$ Az ideális gáz egyenlete kis megváltozásokra: $\begin{array}{c}{\displaystyle \Delta \left(pV\right)=\Delta \left(nRT\right)\mathrm{,}\text{azaz}p\Delta V+V\Delta p=nR\Delta T\mathrm{.}}\end{array}$ A $pV$ 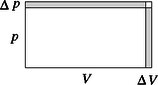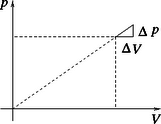szorzatot egy téglalap területének véve azonnal látszik, hogy egy kis területnövekedés a fenti módon kiszámítható (12. ábra). A fenti két egyenletből $\begin{array}{c}{\displaystyle \frac{\Delta p}{\Delta V}=\frac{p}{V}\mathrm{,}}\end{array}$ és mivel az okoskodás a folyamat bármely részén érvényes, a $p-V$ diagram egyenes arányosságot fejez ki (lásd a 13. ábrát). A kezdeti nyomást a $p_0{V}_0=nR{T}_0$ gáztörvényből lehet számolni: $p_0=6\mathrm{,}2\cdot {10}^4\text{Pa}$. A végső térfogat $\left(V\text{'}\right)$ és a végső nyomás $\left(p\text{'}\right)$ között a következő összefüggések állnak fenn: $p\text{'}V\text{'}=nR\left(2T_0\right)$ (gáztörvény), valamint $p/V=p\text{'}/V\text{'}$ ($p$ és $V$ arányossága). Ezekből $V\text{'}=\sqrt[]{2}{V}_0=0\mathrm{,}28{\text{m}}^3$ és $p\text{'}=\sqrt[]{2}{p}_0=8\mathrm{,}8\cdot {10}^4\text{Pa}$ adódik. A folyamat a $p-V$ diagramon a kezdő- és a végállapotnak megfelelő pontok közötti egyenessel írhatjuk le (14. ábra).     A fizika I. kategória végeredménye       1. Mihajlik Gábor (Vác, Boronkay György Műszaki Szakközépiskola, 11. évf.), tanára: Arany Tóth László; 2. Nagy Péter (Budapest, Egressy Gábor Ipari Szakközépiskola, 12. évf.), tanára: Zentai Magdolna; 3. Orbán József (Budapest, Bolyai János Elektronikai Szki., 12. évf.), tanára: Csapó Mária; 4. Hegedűs Miklós (Debrecen, Gábor D. Elektr. Műsz. Középisk., 12. évf); 5. Csibra Norbert (Jászberány, Liska J. Erősáramú Szki. és Gimn., 12. évf.); 6. Bíró Előd (Budapest, Puskás T. Távközl. Techn., 12. évf.); 7. Lovas László (Szeged, Déri M. Ip. Szki., 12. évf.); 8. Sipos Péter (Budapest, Trefort Á. Kéttannyelvű Műsz. Szki. és Gimn., 11. évf); 9. Lugosi Attila (Budapest, Puskás T. Távközl. Techn., 12. évf.); 10. Bodonyi Gábor (Jászberény, Liska J. Erősáramú Szki. és Gimn., 12. évf.).     A fizika II. kategória végeredménye     1. Tóth Bálint (Budapest, Fazekas Mihály Fővárosi Gyakorló Gimn., 11. évf.) tanárai: Dvorák Cecília, Horváth Gábor; 2. Karádi Richárd (Győr, Révai Miklós Gimn., 12. évf.) tanárai: dr. Somogyi Sándor, Nagy Attila; 3. Józsa István Gergő (Debrecen, KLTE Gyakorló Gimn., 11. évf.) tanárai: Farkas József, dr. Szegedi Ervin; 4. Lippner Gábor (Fazekas M. Főv. Gyak. Gimn., 12. évf.); 5. Németh András (Fazekas M. Főv. Gyak. Gimn., 11. évf.); 6. Tóth Ádám (Fazekas M. Főv. Gyak. Gimn., 12. évf.); 7. Császár Balázs (Szombathely, P. R. Szent Norbert Gimn., 12. évf.); 8. Boja Bence (Budapest, Árpád Gimn., 12. évf.); 9. Gáli Gergely (Fazekas M. Főv. Gyak. Gimn., 12. évf.); 10. Bérczi Gergely (Szeged, JATE Ságvári E. Gyak. Gimn., 12. évf.).     A fizika III. kategória végeredménye     1. Bálint Imre (Szeged, JATE Ságvári Endre Gyakorló Gimn., 12. évf) tanára: Homolya Ernő; 2. Kormos Márton (Debrecen, KLTE Gyakorló Gimn., 12. évf.) tanárai: Farkas József, dr. Szegedi Ervin; 3. Somogyi Gábor (Debrecen, Tóth Árpád Gimn., 12. évf.) tanárai: Baló Péter, dr. Szegedi Ervin; 4. Hegedűs József (Fazekas M. Főv. Gyak. Gimn., 12. évf.); 5. Váry Mátyás (Zalaegerszeg, Zrínyi M. Gimn., 12. évf.); 6. Szöllősi Gergely (Debrecen, KLTE Gyak. Gimn., 12. évf.); 7. Nagymányoki Zoltán (Budapest, Veres Péter Gimn., 12. évf.); 8. Vasvári Gergely (Pannonhalma, Bencés Gimn., 12. évf.); 9. Pál András (Budapest, Eötvös J. Gimn., 11. évf.); 10. Pandur Sándor (Budapest, Apáczai Csere J. Gimn., 11. évf.).   Holics László