A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.
1. feladat. Arányosság (egymástól független, rövid feladatok)
(a) Egy ideális, súlytalan rugó végére függesztett pontszerű test frekvenciával fel-le rezeg. Mekkora lesz az új frekvencia, ha a rugót félbevágjuk, és a végére visszaakasztjuk a testet?
(b) A hidrogénatom sugara alapállapotban nm (a ,,Bohr-sugár"). A ,,müonhidrogén" egy olyan hidrogénatom, melyben az elektront egy vele azonos töltésű, de 207-szer nagyobb tömegű részecskével, a müonnal helyettesítjük. Mekkora a müonhidrogén sugara? Felhasználhatjuk, hogy a proton tömege mind az elektron, mind a müon tömegénél sokkal nagyobb.
(c) A Föld átlaghőmérséklete K. Mekkora lenne az új átlaghőmérséklet, ha a Nap és a Föld átlagos távolsága -kal lecsökkenne?
(d) Egy napon a levegő száraz, és a sűrűsége kg/m. Másnapra megnő a levegő páratartalma, 2 tömegszázalék vízgőzt tartalmaz. A hőmérséklet és a nyomás nem változott. Mekkora lett a levegő sűrűsége? (A száraz levegő átlagos moláris tömege 28,8 g/mol, a víz moláris tömege 18 g/mol. Feltételezhetjük, hogy ideális gázokról van szó.)
(e) Egy bizonyos helikopter akkor tud lebegni, ha a motorja mechanikai teljesítményt ad le. Egy másik helikopter ennek pontosan -ére kicsinyített mása (minden lineáris mérete fele akkora). Mekkora mechanikai teljesítmény szükséges ahhoz, hogy ez a helikopter lebegjen?
Versenyen kívüli pótfeladat: Egy űrhajós űrruhába öltözve a Földön m/s sebességgel tud a ,,legkényelmesebben'' sétálni. Mekkora lesz a legkényelmesebb sétálás sebessége a Holdon, ahol a nehézségi gyorsulás a földi érték -a?
Megoldás. (a) Legyen az eredeti rugó hossza , rugóállandója pedig . A rugó végére helyezett tömegű test rezgési frekvenciája A rugóállandó a rugóban ébredő erő és a megnyúlás hányadosa: . A rugó középpontja ugyanekkora erő hatására csak távolsággal mozdul el, a fele hosszúságú rugóra tehát . Eszerint a megrövidített rugó végén rezgő test frekvenciája:
(b) A Bohr-modell szerint az kvantumfeltétel és az mozgásegyenlet együtt meghatározza az atommag körül keringő tömegű részecske és az alapállapoti pályasugár közötti kapcsolatot:
Megjegyzés: Ugyanehhez az eredményhez a de Broglie-féle anyaghullámokra és a Heisenberg-féle határozatlansági relációra hivatkozva is eljuthatunk. Egy sugarú atomban az tömegű (könnyű) részecske nagyságrendileg sebességgel, tehát mozgási energiával, továbbá helyzeti energiával rendelkezik. A helyzeti és a mozgási energia összege kvadratikus függvénye, melynek minimuma: .
Eszerint a müonhidrogén sugara: pm.
(c) Ha a Nap teljesítményét -vel, a Föld pályasugarát -rel jelöljük, akkor a átlaghőmérsékletet megadó (a beérkező és a kimenő sugárzási teljesítmények egyensúlyát kifejező) egyenlet: | |
A képletben a Föld fényvisszaverő képessége (ún. albedója), a Föld sugara, az emissziós együttható, pedig a Stefan‐Boltzmann-állandó. (Az emisszióképesség a hőmérséklettől is függ, de kis változásoknál ezt elhanyagolhatjuk.) A fenti összefüggés szerint , az pályasugár -os csökkenése tehát a hőmérséklet -os emelkedéséhez vezet: K.
(d) molekulát tartalmazó ideális gáz állapotegyenlete: . Ha két gázmennyiség térfogata, nyomása és hőmérséklete rendre megegyezik, akkor azonos számú molekulát tartalmaznak, sűrűségük tehát arányos kell legyen az átlagos móltömeggel.
Bizonyos térfogatú, tömegű száraz levegőben darab molekula, ugyanekkora térfogatú, tömegű nedves levegőben pedig | |
molekula található. Mivel , a sűrűségek aránya | |
a nedves levegő sűrűsége pedig kg/m.
(e) Ezt a feladatot múlt havi számunkban (FF. 3088. számmal) a pontversenyben is kitűztük, megoldását később közöljük.
Versenyen kívüli pótfeladat: A feladat lényege a ,,legkényelmesebb sétálás'' kifejezés értelmezése. Feltételezzük, hogy a legkényelmesebb (leginkább energia-takarékos) sétálásnál a lábainkat éppen csak megemeljük, de nem fejtünk ki rájuk forgatónyomatékot. Ilyenkor a lábak fizikai ingaként lengenek, periódusidejük , a lépések frekvenciája és ezzel együtt a sétálás sebessége tehát -vel arányos. (A lépések hossza a láb méretétől függ, emiatt természetes az a feltevés, hogy a Holdon is ugyanakkorákat lépünk, mint a Földön.) A kérdéses sebesség: m/s.
2. feladat. Atommagtömegek és stabilitás. Valamennyi energiát MeV-ben, millió elektronvoltban fejeztük ki. J, de ezt nem kell tudni a feladat megoldásához.
1. ábra. Egy nukleonra jutó kötési energia
Egy rendszámú (protonszámú) és neutronszámú () atommag tömegét úgy kapjuk meg, hogy a magot alkotó szabad összetevők (protonok és neutronok) tömegének összegéből kivonjuk a -tel osztott kötési energiát (-et): . Az alábbi grafikon egy adott értékhez tartozó maximális értékét adja meg függvényében. Minél nagyobb értéke, általában annál stabilabb a mag.
(a) Egy bizonyos tömegszám felett a nukleonok kötési energiája elég kicsi ahhoz, hogy a mag kibocsáthasson egy -részecskét (). Lineáris közelítést alkalmazva az -nál nagyobb tömegszámú atomokra, becsüld meg az 1. ábra alapján értékét!
Ebben a közelítésben tételezd fel a következőket:
| * | Az -bomlás kiinduló és keletkező magja is rajta van a megadott görbén. |
| * | Az -részecske teljes kötési energiája: MeV. (Ezt nem tudod a grafikonból kiolvasni!) |
(b) Egy protont és neutront () tartalmazó atommag kötési energiáját a következő félempirikus képlet adja meg: | |
ahol értéke:
| * | páratlan ‐ páratlan magokra, |
| * | 0 páratlan ‐ páros és páros ‐ páratlan magokra, |
| * | páros ‐ páros magokra. |
Az együtthatók értéke: MeV; MeV; MeV; MeV; MeV.
(i) Vezesd le azt az összefüggést, amely adott tömegszám esetében megadja a legnagyobb kötési energiához tartozó protonszámot (rendszámot)! Csak ebben az alkérdésben a -tagot figyelmen kívül hagyhatod.
(ii) Az tömegszámú magok közül melyik -hez tartozik a legnagyobb ? Ebben az esetben vedd figyelembe a -tagot is!
(iii) Tekintsük az alábbi táblázatban szereplő három, tömegszámú atommagot. Határozd meg, hogy közülük melyek az energetikailag stabilak, és melyek rendelkeznek elegendő energiával ahhoz, hogy az alább felsorolt bomlások valamelyikével elbomolhatnak! Határozd meg az (i) pontban definiált -ot, és töltsd ki a válaszlapon található táblázatot!
Jelölés: ZAX X = kémiai vegyjel
A táblázat kitöltésekor kérjük:
| * | •az energetikailag megengedett folyamatokat jelöld így: V, |
| * | •az energetikailag tiltott folyamatokat jelöld így: 0, |
| * | •csak a táblázatban szereplő három mag közötti átmenetekkel foglalkozz! |
Bomlási folyamatok:
(1) β--bomlás: a mag egy elektront bocsát ki,
(2) β+-bomlás: a mag egy pozitront bocsát ki,
(3) β-β--bomlás: a mag egyidejűleg két elektront bocsát ki,
(4) elektronbefogás: a mag az elektronhéjból fog be egy elektront.
Az elektron (és a pozitron) nyugalmi energiája mec2=0,51 MeV, a protoné mpc2=938,27 MeV, a neutroné pedig mnc2=939,57 MeV.
Megoldás. (a) Az alfa-bomlás során A→(A-4)+α(A=4). Ebből adódóan a bomlás energetikai feltétele: mA-mA-4-m4>0. A nukleonok száma és fajtája bomlás közben állandó marad, ezért csak a kötési energiát kell vizsgálnunk: -BA+BA-4+B4>0. Ha B/A-t a lineáris közelítésnek megfelelően B/A=a+bA alakban írjuk, akkor a következő egyenletet kapjuk: | -A(a+bA)+(A-4)(a+b(A-4))+B4>0,-8bA-4a+16b+B4>0. |
Az 1. ábra alapján A=100-nál nagyobb tömegszámú atomokra jó a lineáris közelítés: | B/A=(9,6-0,0080A)MeV,azaza=9,6MeVésb=-0,0080MeV. |
Ebből a bomlás feltétele: 0,064A-38,4-0,1+25,0>0, azaz A>211.
(b) (i) Mivel A értéke rögzített, csak a Z-től függő utolsó előtti két tagot kell figyelembe vennünk. Zmax kifejezését deriválással kaphatjuk meg: | dBdZ=-2ZacA-1/3-aaA(-4A+8Z),Zmax=4aa2acA-1/3+8aaA=A2⋅11+acA2/34aa. |
(ii) a=200 esetében az (i) pontban levezetett képletből Zmax=79,25. De most figyelembe kell vennünk az utolsó tagot is. Így a derivált kifejezése: | dBdZ=-2ZacA-1/3-aaA(-4A+8Z)±2apA-3/4. |
Az utolsó tag akkor pozitív, ha Z értékének +1-gyel való megváltoztatása a magot páratlan‐páratlan magból páros‐páros maggá alakítja, ellenkező esetben negatív.
Hogyan kezelhetjük ezt a tagot?
Zmax értéke egész szám kell legyen, és mivel a páros számok előnyösebbek, Zmax=80-at tippelhetünk. Ellenőrzésképp kiszámíthatjuk az utolsó három tag nagyságát néhány közeli Z értékre:
977,241 978,915 979,295 980,342 981,093 982,512 983,637 979,241 975,915 976,295 975,342 978,093 979,512 984,637
Ez megerősíti, hogy Zmax=80. (Ez egy páros‐páros mag.)
(iii) Tekintsük a kötési energiát megadó képletben csak az utolsó három tagot! A többi állandó, ha A értéke állandó. Nevezzük ezek összegét X-nek. Ahhoz, hogy eldöntsük egy magról, hogy stabil-e, meg kell határoznunk a szomszédos magok X értékeinek különbségét, és ezt össze kell hasonlítanunk az egyes lehetséges bomlások energiaigényével.
(1) β--bomlás: n→p+e-, ΔX>-1,30+0,51=-0,79 MeV szükséges,
(2) β+-bomlás: p→n+e+, ΔX>1,30+0,51=1,81 MeV szükséges,
(3) β-β--bomlás: 2n→2p+2e-, ΔX>2(-1,30+0,51)=-1,58 MeV szükséges,
(4) elektronbefogás: e-+p→n, ΔX>1,30-0,51=0,79 MeV szükséges.
Mag X(MeV) 53128I 491,06 54128Xe 489,16 55128Cs 492,54
Ennek alapján a táblázat helyes kitöltése:
Mag/Folyamat β--bomlás β+-bomlás elektronbefogás β-β--bomlás 53128I V 0 0 V 54128Xe 0 0 0 0 55128Cs 0 V V 0
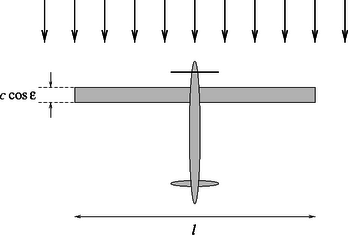
3. feladat. Napenergiával hajtott repülőgép. Olyan repülőgépet tervezünk, amely kizárólag napenergia felhasználásával repül. Az a legcélszerűbb elrendezés, ha a szárnyak felső felületét teljesen beborítják a napelemek. A napelemek által termelt elektromos energia hajtja a légcsavarokat.
2. ábra. A repülűgép felülnézeti képe (a hozzá rögzített koordináta-rendszerben)
Legyen a szárny téglalap alakú, fesztávolsága l, szélessége c, területe S=cl, aránytényezője (aspect ratio) A=l/c. A szárny működését a következő modellel írhatjuk le: egy x magasságú és l szélességű levegőréteg a szárnyon egy kis ε szöggel lefelé eltérül, miközben a sebességének nagysága alig változik. A szárnyon lévő szabályozólemezekkel be lehet állítani a repüléshez optimális ε szöget. Ez az egyszerű modell akkor felel meg legjobban a valóságnak, ha x=π⋅l/4; a továbbiakban ezt az értéket használjuk. A repülőgép teljes tömege M, a sebessége pedig a környező levegőhöz képest v. A számításokban csak a szárny körüli légáramlást vegyed figyelembe! A légcsavar által okozott légáramlásváltozást hanyagold el!
3. ábra. A szárny oldalnézetben (a repülőgéphez rögzített koordináta-rendszerben)
(a) Tegyük föl, hogy a szárnyat elhagyó levegőnek úgy változik meg az impulzusa, hogy a sebességének nagysága nem változik. Vezesd le azokat az összefüggéseket, melyek megadják az L függőleges emelőerőt (lift force) és a vízszintes D1 fékezőerőt (drag force) a szárny méreteinek, valamint v, ε és a levegő ϱ sűrűségének függvényében! Feltételezheted, hogy a levegő áramlásának iránya mindig párhuzamos az oldalnézeti rajz síkjával.
(b) A szárnyfelület mentén mozgó levegő súrlódása egy további D2 vízszintes fékezőerőt eredményez. A levegő egy kicsit lelassul, nagysága Δv értékkel csökken (Δv≪v/100). A relatív sebességváltozást a összefüggés adja meg, ahol f egy ε-tól független állandó.
Jelöljük v0-lal azt a sebességet, mellyel minimális teljesítménnyel lehet állandó magasságban állandó sebességgel repülni! Add meg v0-t M, f, A, S, ϱ és a g nehézségi gyorsulás függvényében! Hanyagold el az ε2-nél és Δv-nél kisebb tagokat!
Hasznos lehet a következő (kis szögekre érvényes) közelítés: 1-cosε≈12sin2ε.
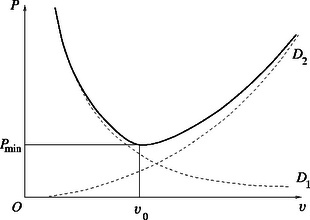
(c) ábrázold vázlatosan a repüléshez szükséges P teljesítményt a v sebesség függvényében! Rajzold be az ábrába azt is, hogy a kétféle fékezőerőből származó teljesítményjárulék külön-külön hogyan függ v-től! Add meg egy képlettel a Pmin minimális teljesítményt M, f, A, S, ϱ és g függvényében!
(d) Tegyük föl, hogy a napelemek annyi energiát termelnek, hogy a légcsavar mechanikai teljesítménye egységnyi szárnyfelületre vonatkoztatva I=10W/m2. Számítsd ki hogy ilyen teljesítmény mellett mekkora a maximális szárnyterhelés Mg/S (N/m2-ben), és mekkora az ehhez tartozó v0 sebesség!
Adatok: ϱ=1,25kg/m3, f=0,004, A=10.
Megoldás. (a) Az egységnyi idő alatt átáramló tömeget nevezzük el ,,tömegáramnak''! Egy dmdt tömegáramú közeg sebességének Δv-vel való megváltoztatásához szükséges erő: F=Δvdmdt. Jelen esetben a tömegáram: A Δv vektor függőleges komponense: ΔvV=vsinε, vízszintes komponense: ΔvH=v(1-cosε).
Ezek alapján felírhatjuk az L függőleges emelőerőt és a vízszintes D1 fékezőerőt: | L=π4ϱv2l2sinε,D1=π4ϱv2l2(1-cosε). |
(b) A repülőgép vízszintes repüléséhez szükséges teljesítmény: P=Dv=(D1+D2)v. A vízszintes D2 fékezőerőt a szárny mellett elhaladó levegő súrlódásából származó impulzus változásából írhatjuk fel: Az anyagmegmaradást kifejező (kontinuitási) egyenlet alapján: Behelyettesítve, hogy v1=v és v2=v-Δv, kapjuk: | D2=vxlϱv-(v-Δv)xlϱv=xlϱv2-xlϱv2+vΔvxlϱ=xlϱvΔv=πl4lϱvΔv=πf4Aϱv2l2. |
Ebben a közelítésben D kifejezhető a tömeg, a sebesség és a szárnyméretek segítségével. Ne felejtsük el, hogy vízszintes repüléskor az emelőerő egyenlő a gép súlyával! | L=Mg=π4ϱv2l2sinε,sinε=4Mgπϱv2l2. |
Ezután már minimalizálhatjuk a teljesítményt akár v, akár ε szerint. Itt most v-t választjuk: | P=Dv=π4ϱv3l2(fA+12(4Mg)2(πϱv2l2)2)=π4ϱv3l2fA+2(Mg)2πϱvl2,dPdv=3π4ϱv2l2fA-2(Mg)2πϱv2l2=0. |
A minimális teljesítményhez tartozó v0 repülési sebességre fennáll: | v04=8(Mg)2A3π2ϱ2l4f=83Af(MgπϱS)2. |
(c)
4. ábra. A teljesítmény a sebesség függvényében
| Pmin=π4ϱv03l2(fA+12(4Mg)2(πϱv02l2)2)=π4ϱv03l2(fA+(4Mg)22(πϱl2)23π2ϱ2l4f8(Mg)2A)==πϱv03l2fA=πϱv03Sf. |
Behelyettesítve v0 értékét: | Pmin=πϱSf83/4(Mg)3/2(3Af)3/4(πϱS)3/2=(83A)3/4f1/4(Mg)3/2(πϱS)1/2. |
(d) A fenti kifejezést egyenlővé téve a rendelkezésre álló IS teljesítménnyel, | (MgS)3/2=I(3A8)3/4(πϱ)1/2f1/4, vagyis MgS=I2/3(3A8)1/2(πϱ)1/3f1/6, |
számszerűen pedig Mg/S=35,6N/m2, v0=8,60 m/s adódik.
A kísérleti fordulóban egy érdekes és különleges eszközzel, a ,,bimorph''-fal végeztek a versenyzők különböző méréseket. A bimorph két vékony piezoelektromos rétegből áll, melyeket egymáshoz ragasztottak. (A piezoelektromos anyagok elektromos térben megváltoztatják méretüket, mechanikai feszültség hatására pedig elektromos potenciálkülönbség alakul ki bennük. Elektromos térben a relatív hosszváltozás első közelítésben arányos a térerősséggel.
A hosszváltozásnak azonban hiszterézise van, ami annyit jelent, hogy ha a rákapcsolt teret nullára csökkentjük, a méretek nem állnak vissza az eredeti értékekre. Az eredeti méret csak egy kis ellenirányú térrel érhető el újra.) Az így kialakított 38 mm hosszú, kb. 2-3 mm széles, 0,8 mm vastag kettősrétegben a két külső felületre gőzölögtetett kontaktusok segítségével elektromos tér hozható létre. A rétegeket úgy választották, hogy a külső felületre merőleges elektromos tér hatására az egyik hosszirányba kitágul, a másik réteg pedig összehúzódik. Ellentétes irányú térben a rétegek alakváltozása is fordított lesz: ami korábban összehúzódott, az kitágul, a másik pedig összehúzódik. Feltételezhető, hogy az elektromos tér hatására a bimorph körív alakúra görbül meg. A bimorph végére egy kicsiny tükröt ragasztottak. A tükörről visszaverődő lézersugár segítségével a bimorph néhány μm-es elmozdulását is mérni lehetett.
Feladatok:
1. Határozd meg, hogyan függ a bimorph szabad végének elmozdulása a rákapcsolt feszültségtől, +36 V-tól lefelé -36 V-ig és utána vissza, felfelé +36 V-ig! A mérések során a feszültséget csak a megjelölt irányba változtasd! (Például ha -36 V-tól +36 V-ig mérsz, mindig növeld a feszültséget, sohase csökkentsd azt. Ha egy mérési pontot kihagysz, ne térj vissza rá!) ábrázold a mért függvénykapcsolatot milliméterpapíron!
Egy ciklus alatt (+36 V-tól le -36 V-ig és vissza +36 V-ig változó feszültségnél) bizonyos energia disszipálódik a bimorph-ban. Adj meg és számolj ki egy olyan mennyiséget, amely ezzel az energiaveszteséggel arányos!
2. Egy adott bimorph-nál ‐ ha a hiszterézist elhanyagoljuk ‐ a bimorph szabad végének elmozdulását a d=AVmln, ahol V az alkalmazott elektromos feszültség, l a bimorph szabad részének a hossza (a csipesszel érintkező legszélső ponttól mérve), továbbá m, n és A konstansok. Megfelelő mérésekkel és számításokkal határozd meg az m, n és A állandók számértékét!
3. Mérd meg a bimorph kapacitását!
Rendelkezésre álló eszközök:
| * | • Egy L=(38±1) mm hosszú bimorph. A bimorph egyik végéhez egy kis tükröt erősítettek. A bimorph-ot egy ruhacsipesz tartóba fogták, kontaktusokkal és vezetékekkel látták el. A bimorph szabad részének l hosszát úgy tudod megváltoztatni, hogy a csipeszben elmozdítod. Légy óvatos, mert a bimorph nagyon kényes! |
| * | • Egy lézer mutató (egy körétekert gumikarikával, melynek segítségével a lézert a mérés idején folyamatosan bekapcsolva tarthatod). |
| * | • Fekete gyurma a csipesz és a lézer asztalon való rögzítéséhez. |
| * | • Egy ernyő (használd milliméterpapírt, melyet az asztalok közötti térelválasztóra rögzíthetsz). |
| * | • Egy multiméter vezetékekkel. (Egyenfeszültség méréséhez a multiméter kapcsolóját fordítsd el úgy, hogy a kis kör DCV terület 200-as értékére mutasson. A voltmérő bemenő ellenállása 1MΩ, a mérési pontosság ±0,1 V). |
| * | • Egy 2,5MΩ-os változtatható ellenállás (potméter), a bimorph feszültségének szabályozására, három kivezetéssel. A piros vezeték a potméter középső (csúszó) kivezetése. |
| * | • Négy darab 9 V-os telepből álló egység (Megjegyzés: A feszültségforrás belső ellenállását egy 5kΩ-os ellenállással megnövelték, melyet az egyik vezetékbe kötöttek be. Ez korlátozza az áramot és védi az áramkört. NE zárd rövidre és ne kapcsold ki ezt az ellenállást!) |
| * | • Egy (1,00±0,05)GΩ-os ellenállás. (Figyelem! Az ellenállás értékét megváltoztathatja a bőrödről rárakódó szennyeződés, ezért ne érj hozzá az ellenállás testéhez, csak a fém kivezetésekhez!) |
Részfeladatok:
1.1. Rajzold le annak az áramkörnek a vázlatát, melyet a bimorph szabad végének elmozdulása és a feszültség közti kapcsolat mérésénél használtál!
1.2. Vázlatosan ábrázold a mérés geometriai elrendezését, és jelöld be az általad használt összes mennyiséget!
1.3. Add meg azt az összefüggést, amely kapcsolatot teremt a bimorph szabad végének elmozdulása és a mért mennyiségek között!
1.4. ábrázold milliméterpapíron a bimorph szabad végének elmozdulását a feszültség függvényében! Jelöld be, mely pontok felelnek meg a növekvő és melyek a csökkenő feszültségnek! Ne felejtsd el a tengelyeken feltüntetni a léptéket és a mértékegységeket!
1.5. Add meg, hogy melyik mennyiség az, amely arányos a bimorph által elnyelt energiával!
1.6. Írd le a bimorph által disszipált energiával arányos mennyiség számértékét, mérési hibával és mértékegységgel együtt!
2.1. Add meg m számértékét! Add meg, milyen adattáblázatokat, grafikonokat és számításokat használtál ehhez!
2.2. Add meg n számértékét, mérési hibával együtt! Add meg, milyen adattáblázatokat, grafikonokat és számításokat használtál ehhez!
2.3. Add meg az A konstans számértékét, mérési hibával és mértékegységgel együtt!
3.1. Rajzold le a bimorph kapacitásának mérésénél használt áramkör vázlatát!
3.2. Add meg, hogy milyen mennyiségeket mértél és milyen összefüggést használtál a bimorph kapacitásának meghatározásánál! Add meg, milyen adattáblázatokat, grafikonokat és számításokat használtál ehhez!
3.3. Add meg a kapacitás számértékét, mérési hibával és mértékegységgel együtt!
Megoldás. A feladat megoldása elsősorban nem elméleti, hanem gyakorlati nehézségeket okozott. Az eszközöket egy fekete, gyurmaszerű anyaggal kellett az asztalhoz rögzíteni, és a mérés pontossága szempontjából egyáltalán nem volt mindegy, hogy ebből a nyúlós anyagból ki mennyit és hol használt. (μm pontossággal kellett mérni!)
Természetesen a pontatlan, nagy hibákat tartalmazó mérési eredményeket sokkal nehezebb feldolgozni. (Milyen rossz, ha valaki elvi megfontolásokból tudja, hogy minek kellene kijönni, és mégis egészen más eredményt kap!)
A legnagyobb ötlet a 3. kérdés megválaszolásához kellett. A bimorph kapacitása kb. 5 nF ‐ elég kicsi érték. Ha a 36 V feszültségre feltöltött bimorph-ot az 1MΩ ellenállású feszültségmérőn keresztül sütjük ki, az időállandó olyan rövid, hogy stopperórával nem mérhető. A megoldás az, hogy a bimorph-ot a rendelkezésre álló 1GΩ-os ellenálláson keresztül sütjük ki, és a bimorph feszültségét közvetetten, az első feladathoz hasonlóan, optikai úton mérjük, és a feszültségmérőt nem is használjuk.
| Gnädig Péter ‐ Vankó Péter |
A feladat szövegében és a megoldásban megtartottuk az angol elnevezésekre utaló eredeti jelöléseket. Ezek eltérnek a nálunk szokásos jelölésektől, de mivel az olimpián a rendezők elvárják az általuk megadott jelölések használatát, a leendő versenyzők felkészülésének ,,megkönnyítése'' érdekében nem ,,fordítottuk le'' a betűjeleket. |
 PDF | MathML
PDF | MathML