Kezdőlap


Cím:	1996. Beszámoló az Eötvös-versenyről
Szerző(k):	Radnai Gyula
Füzet:	1997/március, 175 - 181. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

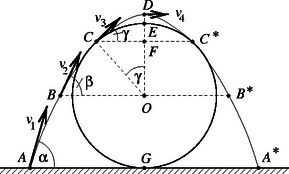
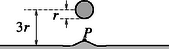
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1996 október 25-én rendezte meg az Eötvös Loránd Fizikai Társulat hagyományos őszi tanulóversenyét, az Eötvös versenyt. Budapesten kívül 14 vidéki városban zajlott egyidőben a verseny, amelyen az 1996-ban érettségizettek és középiskolai tanulók vehettek részt. Indulhattak Magyarországon tanuló külföldi diákok és külföldön tanuló magyar, illetve magyar anyanyelvű diákok is. Minden magukkal hozott segédeszközt ‐ tankönyveket, jegyzeteket, zsebszámológépet ‐ szabadon használhattak. Összesen 300 perc állt rendelkezésre a Versenybizottság által kitűzött három feladat megoldására.
Ismertetjük a feladatokat, a feladat helyes megoldását, majd a verseny végeredményét.

1. A földön vízszintes helyzetében egy 20 cm átmérőjű fatörzs fekszik. Legalább mekkora sebességgel kell elugorjon egy szöcske a földről, hogy át tudja ugrani a fatörzset? (A légellenállást hanyagoljuk el!)

Megoldás. A légellenállást elhanyagolva állíthatjuk, hogy a szöcske pályája parabolaív lesz. Első gondolatunk az, hogy egy olyan parabola adja a kívánt megoldást, amely a hengert legfelül, egyetlen pontban érinti. (Éppen átcsúszik a szöcske a fatörzs felett.) Ezt a sejtést azonban még be kell bizonyítani, mint ahogy az is kiderülhet, hogy nem is igaz. Ezért csak annyit tételezünk fel, hogy a kívánt pálya a fatörzs két oldalán, ugyanolyan magasságban érinti a fatörzset (1. ábra).
Az ábrán

C

és

C^{*}

jelöli az érintési pontokat. A szöcske az

A

pontból ugrik el,

v_{1}

kezdősebességgel, a vízszintessel

α

szöget bezáró irányban. A fatörzs tengelyével azonos magasságban lévő

B

(és

B^{*}

) pontban a szöcske sebessége

v_{2}

, a vízszintessel bezárt szög

β

. Az érintési pontokban a sebesség

v_{3}

, a vízszintessel bezárt szög

γ

. A parabolapálya legfelső (

D

) pontjában a sebesség vízszintes irányú, nagysága

v_{4}

.
A feladatban

v_{1}

minimális értékét kell meghatározni. (

v_{1}

ismeretében

v_{2}

v_{3}

v_{4}

az energiatétel felhasználásával kapható meg, azonban ezek kiszámítása nem volt feladat.)
Mi legyen a független változó, aminek függvényében

v_{1}

szélsőértékét keressük? Lehetne az elugrás helye, vagyis például az

A G

távolság. Lehetne az elugrás szöge, amit az ábrán

α

-val jelöltünk. De lehetne akár a

β

, akár a

γ

szög is: akármelyik szög meghatározza a másik kettőt. A független változó szerencsés megválasztása lerövidítheti a számításokat.
Válasszuk független változónak a

γ

szöget! Ezzel ugyanis

v_{3}

kifejezhető,

v_{3}

segítségével pedig felírható

v_{1}

. Lássuk először

v_{3}

és

γ

kapcsolatát.
A

C D

hajítási pályán

t_{3}

-mal jelölve az emelkedés idejét, a függőleges sebességkomponens a

C

pontban

\begin{matrix} v_{3} \cdot sin γ = g t_{3}, \end{matrix}

a vízszintes irányú

C F

elmozdulás pedig

\begin{matrix} v_{3} \cdot cos γ \cdot t_{3} = R \cdot sin γ . \end{matrix}

E két egyenlet összevetéséből kapjuk:

\begin{matrix} v_{3}^{2} = \frac{g R}{cos γ} . \end{matrix}

Most írjuk fel az energiatételt az

A

és a

C

pont között:

\begin{matrix} \frac{1}{2} m v_{1}^{2} = \frac{1}{2} m v_{3}^{2} + m g (R + R cos γ) \end{matrix}

Ebből

\begin{matrix} \begin{matrix} v_{1}^{2} & = v_{3}^{2} + 2 g R (1 + cos γ), \\ v_{1}^{2} & = \frac{g R}{cos γ} + 2 g R (1 + cos γ), \\ v_{1}^{2} & = 2 g R (1 + cos γ + \frac{1}{2 cos γ}) . \end{matrix} \end{matrix}

Mekkora

γ

szögnél lesz

v_{1}

a legkisebb? (Első sejtésünk szerint

γ = 0

esetben, amikor épp átcsúszik a szöcske a fatörzs tetején. Ekkor

cos 0 + \frac{1}{2 cos 0} = 1,5

. A kérdés az, hogy lehet-e

cos γ + \frac{1}{2 cos γ} < 1,5

.)
Írjuk fel a számtani és a mértani közép közötti egyenlőtlenséget

cos γ

és

\frac{1}{2 cos γ}

esetén! (Feltéve, hogy egyik sem negatív, ami azért igaz, mert

cos γ

nem negatív, ami viszont

0 \leq γ \leq 90^{\circ}

-ból következik.)

\begin{matrix} \frac{cos γ + \frac{1}{2 cos γ}}{2} \geq \sqrt[]{cos γ \frac{1}{2 cos γ}} = \frac{\sqrt[]{2}}{2} . \end{matrix}

cos γ + \frac{1}{2 cos γ}

legkisebb értéke tehát

\sqrt[]{2}

, ezt

γ = 45^{\circ}

-nál veszi fel. Azt a meglepő eredményt kaptuk tehát, hogy az optimális pálya a legfelső pontjában nem érinti a fatörzset, hanem fölé emelkedik. A szöcske helyzeti energiája a legmagasabb pontban nagyobb ugyan, mint az ,,éppen átcsúszik'' esetben, de a mozgási energiája ‐ s az összenergiája is ‐ kisebb! Az eredeti kérdésre a helyes válasz tehát:

\begin{matrix} v_{1_{{min}_{}^{}}} = \sqrt[]{2 g R (1 + \sqrt[]{2})} \approx 2,2 \frac{m}{s} . \end{matrix}

Az érdekesség kedvéért kiszámíthatjuk

α

és

β

megfelelő értékeit is ebben az esetben:

\begin{matrix} α = 67, 5^{\circ} (= \frac{3 π}{8}), β = 60^{\circ} (= \frac{π}{3}); \end{matrix}

az elugrási

A G

távolság pedig

R (1 + \frac{\sqrt[]{2}}{2}) \approx 17

cm. Az ábrán jelölt

F

pont a parabola fókuszpontja lesz.

2. Egy 3 dm magas, hengeres, zárt edényben 300 K hőmérsékletű,

10^{5}

Pa nyomású levegő van. Kívülről történő hűtéssel, illetve fűtéssel az alaplap hőmérsékletét 270 K-re csökkentjük, a fedőlapét 330 K-re növeljük, és a továbbiakban folyamatosan ezen a hőmérsékleten tartjuk. (Az edény oldalfala hőszigetelő.)
a) Megváltozik-e a gáz nyomása az eredeti állapothoz képest?
b) Becsüljük meg, hogy mennyivel tolódik el a bezárt gáz tömegközéppontja!

Megoldás. A gáz az edényben kezdetben egyensúlyi állapotban van. Hőmérséklete és nyomása is az edényben mindenütt ugyanannyi. (A nehézségi erőtérben szükségképpen fellépő függőleges nyomásgradienstől eltekinthetünk: erre utal, hogy a feladat szövegében szerepel a mindenütt egyenlő nyomás konkrét értéke.)
A végállapot már nem egyensúlyi állapot. A nyomás ugyan most is ugyanannyi mindenütt az edényben, a hőmérséklet azonban nem: lentről felfelé 270 K-től 330 K-ig nő. A beállt végállapotban szerencsére a hőmérséklet bármely helyen időben már nem változik. Az ilyen ‐ nem egyensúlyi ‐ állapotot nevezik stacionárius állapotnak, amelyre azonban még fennáll az egyensúlyi állapotra bevezetett

\begin{matrix} E = \frac{f}{2} p V \end{matrix}

összefüggés. Elveszti értelmét azonban a gáz egészére vonatkozólag a

\begin{matrix} p V = N k T \end{matrix}

összefüggés, mivel nincs a gáznak egyetlen, jól meghatározott hőmérséklete.
Feltételezhetjük, hogy a stacionárius végállapot is mintegy egyensúlyi állapotban lévő vízszintes rétegekből tevődik össze. Egy-egy ilyen rétegen belül a hőmérséklet állandó; a magasabban lévő réteg hőmérséklete feladatunk esetében mindig nagyobb lesz.
Elfogadható (,,plauzibilis'') feltevésnek látszik, hogy a rétegek hőmérséklete a magasság lineáris függvénye. (Ez akkor igaz, ha a gáz hővezetőképessége nem függ a hőmérséklettől. A tapasztalat szerint a vizsgált hőmérséklettartományban ez jó közelítéssel teljesül.) Ezt felhasználva válaszolhatunk az a) kérdésre.
Hasonlítsunk össze két olyan (

Δ x

vastagságú) réteget, amelyek az alap- és a fedőlaptól egyenlő (

x \leq \frac{h}{2}

) távolságra vannak! A felső rétegben a hőmérséklet nagyobb, mint az alsóban, ezért itt kevesebb részecske hozza létre ugyanazt a nyomást, mint alul.

\begin{matrix} \begin{matrix} Δ N_{fent} & = \frac{p A Δ x}{k T_{fent}} \\ Δ N_{lent} & = \frac{p A Δ x}{k T_{lent}} \end{matrix}} T_{fent} > T_{lent} \Rightarrow Δ N_{fent} < Δ N_{lent} \end{matrix}

Az edény fele magasságában egyezik meg a hőmérséklet a kiindulási, egyensúlyi állapotbeli hőmérséklettel. Azt mondhatjuk, hogy az edény felső felében a gáz felmelegedett, az alsóban lehűlt. De az előbb beláttuk, hogy a felső rétegekben mindig kevesebb gázmolekula van, mint a megfelelő alsó rétegekben ‐ így azt is mondhatjuk, hogy több gáz hűlt el, mint amennyi felmelegedett!
Így arra a következtetésre jutottunk, hogy az egész gáz belső energiája csökkent. Mivel

E = \frac{f}{2} p V

a stacionárius végállapotban is fennáll, a kisebb

E

-hez kisebb

p

-nek kell tartoznia (

f

és

V

változatlanok). Tehát a gáz nyomása is csökkent.
b) Becsüljük meg, mennyivel tolódott el a gáz tömegközéppontja!
A becslést úgy végezzük, hogy a gázt egyenlő vastagságú, vízszintes rétegekre osztjuk fel. Feltesszük, hogy egy-egy rétegen belül egyensúly van, a réteg hőmérséklete állandó. A felosztást finomítva kaphatunk egyre pontosabb becsléseket.
Példaképpen nézzük az első, durva becslést, amikor csupán két ,,rétegre'' osztjuk fel a hengert: legyen az edény alsó felében 285 K, a felső felében 315 K a hőmérséklet. A két rétegben levő tömegek aránya:

\begin{matrix} \frac{m_{fent}}{m_{lent}} = \frac{285}{315} = \frac{7,5 cm - Δ h}{7,5 cm + Δ h}, ahonnan Δ h = 0,4 cm . \end{matrix}

Második közelítésben osszuk három egyenlő részre a hengert; a középső réteg hőmérséklete legyen 300 K, a felsőé 330 K, az alsóé 270 K. Az előzőhöz hasonló gondolatmenettel a tömegközéppont süllyedésére

Δ h = 0,67

cm adódik.
Harmadik közelítésben osszuk öt egyenlő vastag rétegre a hengert; az egyes rétegek hőmérséklete fentről lefelé legyen: 330 K, 315 K, 300 K, 285 K, 270 K. Ebben az esetben valamivel hosszabb számolás után

Δ h = 0,60

cm-t kapunk.
Meddig folytassuk ezt? Becslésnek már az elsőnek kapott

0,4

cm is elfogadható. A pontos eredmény (amelynek meghatározását nem kérte a feladat!) integrálszámítással kapható, értéke

Δ h = 0,5

cm.

3. Szigetelő fonálon függő, 1 cm átmérőjű műanyag golyó felszínén

10^{- 8}

C töltés helyezkedik el egyenletesen. A golyót egy széles, nagy tálban lévő sós víz fölé engedjük úgy, hogy az alja 1 cm-re legyen a víztől. A víz felszíne a golyó alatt egy picit megemelkedik. Mekkora ez az emelkedés? (A felületi feszültség szerepét elhanyagolhatjuk, a sós víz sűrűségét vehetjük

1000 {kg/m}^{3}

-nek.)

Megoldás. A sós víz elektromosan jól vezető folyadék (elektrolit). Mind a pozitív, mind a negatív töltéshordozók (ionok) könnyen elmozdulnak benne. A közeledő, feltöltött golyó hatására az általa vonzott, vele ellentétes töltésű ionok igyekeznek a golyó felé elmozdulni, míg a golyóval azonos töltésű ionok a taszító erő hatására ellenkező irányban mozdulnak el. Ezáltal megszűnik a folyadék ,,térfogati semlegessége'' úgy, hogy
1. az eredő elektromos tér erővonalai a golyó és a folyadék közötti térben merőlegesen futnak be a folyadék felszínére;
2. a folyadék belsejében a felszín alatti tartományokban zérus lesz az eredő térerősség.
Természetesen ekkor a golyó a vele ellentétes töltésű folyadékfelszínt magához akarja vonzani, fel akarja emelni. Fel is emeli egy picit; ezt a hatást akadályozza a folyadék felületi feszültsége, valamint a felemelt folyadék saját súlya. Feladatunkban a felületi feszültség szerepét elhanyagolhatjuk, így a folyadék felszíne a golyó alatt addig emelkedik fel, amíg a felületegységre ható elektrosztatikus emelő erő egyenlő nem lesz a felemelkedett folyadékréteg hidrosztatikai nyomásával.
Nem tudjuk, hogy milyen lesz pontosan a kialakuló folyadékfelület alakja. Biztos, hogy kevéssé tér el a síkfelülettől, erre utal a feladat szövege is (,,picit'' megemelkedik) ‐ tehát a levegőben kialakuló eredő elektromos tér meghatározásához alkalmazhatjuk a (sík) tükörtöltés módszerét. Másrészt elegendő lesz figyelmünket egyetlen pontra, a felemelkedő folyadékfelület legfelső

P

pontjára koncentrálni; ennek emelkedése az, amit ki kell számítanunk.
A 2. ábrán

P

-vel jelölt pontban a

Q

töltéstől származó térerősség

\begin{matrix} E_{1} = \frac{1}{4 π ε_{0}} \frac{Q}{{(3 r)}^{2}} . \end{matrix}

A folyadék felületén kialakuló töltéseloszlás hatását a felszín alatt

3 r

mélységben elképzelt

- Q

nagyságú tükörtöltés hatásával helyettesítjük (3. ábra). A tükörtöltéstől származó térerősség a

P

pontban ugyanakkora és ugyanolyan irányú, mint

E_{1}

. Ezért az eredő térerősség:

\begin{matrix} E = 2 E_{1} = \frac{1}{2 π ε_{0}} \frac{Q}{{(3 r)}^{2}} . \end{matrix}

A felületegységre jutó töltés a

P

pontban Gauss tétele alapján:

\begin{matrix} σ = ε_{0} E = \frac{1}{2 π} \frac{Q}{{(3 r)}^{2}} . \end{matrix}

A folyadék felszínén a felületegységre ható erő a

σ

felületi töltéssűrűség és a golyótól származó

E_{1}

elektromos térerősség szorzata:

\begin{matrix} \frac{F}{A} = σ E_{1} . \end{matrix}

Ez az a felületegységre jutó, függőlegesen felfelé emelő erő a

P

pontban, amely egyensúly esetén egyenlő lesz a

P

pontbeli

h

emelkedésből származó hidrosztatikai nyomással:

\begin{matrix} \frac{F}{A} = ϱ g h . \end{matrix}

A sós víz felszínének

h

emelkedését tehát az alábbi egyenletből számíthatjuk ki:

\begin{matrix} \frac{1}{4 π ε_{0}} \frac{Q}{{(3 r)}^{2}} \cdot ε_{0} \cdot 2 \frac{1}{4 π ε_{0}} \frac{Q}{{(3 r)}^{2}} = ϱ g h . \end{matrix}

A megadott, illetve ismert értékeket behelyettesítve az emelkedés magasságára kapjuk:

\begin{matrix} h \approx 0,29 mm . \end{matrix}

Ez az érték valóban ,,pici'' a golyó sugarához, illetve a víztől mért távolságához képest, jogos volt a síktükör-töltés közelítés. (Hasonlóképp jogos volt a golyó töltését a középpontjába helyezett ponttöltéssel helyettesíteni: műanyag golyóról lévén szó, a víz felszínén kialakuló töltéssűrűség vonzása nem tudja átrendezni, megváltoztatni a szigetelőre felvitt egyenletes töltéseloszlást. Azt is be lehet látni, hogy a víz megemelkedéséből adódó görbületi nyomás a hidrosztatikai nyomásnál sokkal kisebb, a felületi feszültség szerepét tehát jogosan hanyagoltuk el.)

A verseny végeredménye

Első díjat nyert
Kurucz Zoltán, az ELTE fizikus hallgatója, aki Szolnokon, a Varga Katalin Gimnáziumban érettségizett, mint Vincze Gábor tanítványa.
Második díjat nyertek egyenlő (2‐4.) helyezésben:
Biró Domokos Botond a Kolozsvári Műszaki Egyetem számítástechnika‐automatizálás szakos hallgatója, aki Marosvásárhelyen, a Bolyai Farkas Elméleti Líceumban érettségizett, mint Bíró Tibor tanítványa;
Tóth Gábor Zsolt, az ELTE fizikus hallgatója, aki Budapesten, az Árpád Gimnáziumban érettségizett, mint Vankó Péter tanítványa;
Varga Tamás, az ELTE fizikus hallgatója, aki Révkomáromban, a Selye János Gimnáziumban érettségizett, mint Szabó Endre tanítványa.
Harmadik díjat nyertek egyenlő (5‐10.) helyezésben:
Gröller Ákos, az ELTE matematikus hallgatója, aki Budapesten, a Fazekas Mihály Fővárosi Gyakorló Gimnáziumban érettségizett, mint Horváth Gábor tanítványa;
Hochsteiger Ákos, a szekszárdi Garay János Gimnázium IV. osztályos tanulója, Pesti Gyula tanítványa;
Kovács András, a BME műszaki informatika szakos hallgatója, aki Budapesten, a Fazekas Mihály Fővárosi Gyakorló Gimnáziumban érettségizett, mint Horváth Gábor tanítványa;
Mátrai Tamás, a budapesti, a Fazekas Mihály Fővárosi Gyakorló Gimnázium IV. osztályos tanulója, Horváth Gábor tanítványa;
Négyesi Gábor, az egri Szilágyi Erzsébet Gimnázium IV. osztályos tanulója, Flaskay Miklós és Burom Mária tanítványa;
Sexty Dénes, az egri Neumann János Közgazdasági Szakközépiskola és Gimnázium IV. osztályos tanulója, Pecsenye Pálné tanítványa.
Négyesi G., Sexty D., Gröller Á., Kovács A.,

Varga T., Kurucz Z., Biró D. B., Hochsteiger Á.,

Tóth G. Zs., Kálmán B., Nagy Z., Nagy Sz., Nyakas P.
Dicséretben részesültek egyenlő (11‐15.) helyezésben:
Kálmán Barnabás, a BME műszaki informatika szakos hallgatója, aki Budapesten, az ELTE Apáczai Csere János Gyakorló Gimnáziumában érettségizett, mint Flórik György tanítványa; Nagy Szilvia, a BME mérnök‐fizikus hallgatója, aki Győrben, a Révai Miklós Gimnáziumban érettségizett, mint Kolozsváry Ernőné és Székely László tanítványa; Nagy Zoltán, a JATE fizikus hallgatója, aki Szegeden, a JATE Ságvári Endre Gyakorló Gimnáziumában érettségizett, mint Homolya Ernő tanítványa; Nyakas Péter, a zalaegerszegi Zrínyi Miklós Gimnázium IV. osztályos tanulója, Vadvári Tibor tanítványa; Wagner Róbert, a pannonhalmi Bencés Gimnázium IV. osztályos tanulója, Hirka Antal és Rábai László tanítványa.
Az ünnepélyes eredményhirdetésre 1996. november 29-én került sor. Itt nemcsak a feladatok helyes megoldásával ismerkedhettek meg a megjelent diákok és tanárok, de egy lézer fényének felhasználásával megfigyelhették a sós víz felszínének pici felemelkedését is.
Megemlékeztünk a 100 évvel ezelőtti Eötvös-verseny nyerteseiről: Visnya Aladárról és Zemplén Győzőről. A díjak átadására a Versenybizottság két volt Eötvös verseny nyertest kért fel; Bakos Tibor éppen 70 évvel ezelőtt, 1926-ban ismételte meg Teller Ede előző évi bravúrját: fizikából is és matematikából is megnyerte az I. díjat a Társulat őszi tanulóversenyén, és ugyanez sikerült 1940-ben Hoffmann Tibornak is. Az Eötvös Társulaton kívül a Nemzeti Tankönyvkiadó is hozzájárult a nyertesek jutalmazásához. A diákokat felkészítő tanárok három meghívott kiadó ajándékkönyveiből válogattak: a Nemzeti Tankönyvkiadó, a Calibra és a Talentum legújabb ismeretterjesztő és tankönyveit hozták el az eredményhirdetésre.
Két régi verseny-nyertes, Hoffmann Tibor és Bakos Tibor, valamint a versenybizottság elnöke (e cikk szerzője) gratulál az idei győztesnek, Kurucz Zoltánnak
A Duna Televízió most már harmadik éve saját híradójában tudósítja határainkon inneni és túli nézőit az ünnepi eseményről. Köszönet érte!

Radnai Gyula