Kezdőlap


Cím:	Beszámoló az 1995-96. tanévi fizika OKTV-ről
Szerző(k):	Holics László
Füzet:	1997/január, 44 - 51. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A fizika OKTV-t az előző évek gyakorlatához hasonlóan az elmúlt tanévben is három kategóriában és három fordulóban rendezték meg. Az első (iskolai) és a második (megyei) fordulón elméleti problémákat, a harmadik fordulón pedig mérési feladatokat oldottak meg a versenyzők. A végső sorrendet a második és a harmadik fordulóban elért pontszám összege alapján állapította meg a versenybizottság.

Az alábbiakban ismertetjük a verseny II. fordulójának feladatait és azok megoldását.^{$^{*}$}A III. (kísérleti) fordulóról a FIZIKA Módszertani Lapok 1996. szeptemberi számában olvasható részletes beszámoló.

Az I. kategória (szakközépiskolások) feladatai

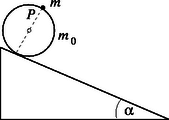
1. feladat. Egy

m_{0}

tömegű karika csúszásmentesen legördül egy

α

hajlásszögű lejtőn. Az indulás pillanatában a

P

pontra száll egy

m

tömegű bogár. Milyen erővel kell kapaszkodnia a bogárnak

5 / 4

fordulat befejezésekor, hogy megtartsa magát a karikán? (

α = 20^{\circ}

m = 1 g

m_{0} ≫ m

(Jurisits József)

Megoldás. A bogár szerepe elhanyagolható a karika mozgásában. A karika

a

gyorsulására és

β

szöggyorsulására felírható egyenletek:

\begin{matrix} m_{0} g sin α - S = m_{0} a, S R = m_{0} R^{2} β, a = R β, \end{matrix}

ahol

a

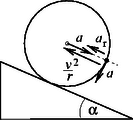
a karika középpontjának gyorsulása. Az egyenletrendszerből adódik, hogy:

\begin{matrix} a = \frac{g sin α}{2} . \end{matrix}

(1)

5 / 4

fordulat, vagyis

s = 5 R π / 2

út megtétele után a középpont sebességének négyzete:

\begin{matrix} v^{2} = 2 a s = \frac{5}{2} R π g sin α . \end{matrix}

(2)

A kérdéses időpillanatban a bogár gyorsulásának radiális komponense egy egyenesbe esik a karika középpontjának gyorsulásával és a karika bogár által elfoglalt pontjának (a karikával együtt haladó ‐ de nem forgó ‐ koordináta-rendszerben mért) centripetális gyorsulásával (2. ábra). Ez utóbbi iránya ellentétes a középpont lejtő menti gyorsulásával, tehát a bogárnak ebben a pillanatban az inerciarendszerben középpont irányában (vagyis a lejtő mentén):

a_{r} = v^{2} / R - a

, a karika érintőjének irányában (vagyis a lejtőre merőlegesen) pedig

a

gyorsulása van.
Vegyük fel koordináta-rendszerünket a lejtőhöz rögzítve, azzal párhuzamos

x

és rá merőleges

y

tengelyekkel (3. ábra)! A bogár gyorsulását a nehézségi erővel együtt a kapaszkodással biztosított

K

erő hozza létre, amelynek komponensei

K_{x}

és

K_{y}

nagyságúak.
A bogár mozgásegyenlete

x

és

y

irányokra:

\begin{matrix} \begin{matrix} (3) K_{x} - m g sin α = m (\frac{v^{2}}{R} - a), \\ (4) m g cos α - K_{y} = m a . \end{matrix} \end{matrix}

(3)-ból (1) és (2) behelyettesítésével:

\begin{matrix} \begin{matrix} K_{x} = m g sin α + m \frac{5}{2} π g sin α - m \frac{g sin α}{2} = 2,8 \cdot 10^{- 2} N, \\ (4)-ből pedig K_{y} = m g (cos α - \frac{sin α}{2}) = 7,5 \cdot 10^{- 3} N . \end{matrix} \end{matrix}

Az eredő kapaszkodási erő:

K = \sqrt[]{K_{x}^{2} + K_{y}^{2}} = 2,9 \cdot 10^{- 2}

N. (Látható, hogy ekkora sebességnél már a sugárirányú gyorsulás dominál.) Az eredő erő iránya a lejtő lapjához viszonyítva:

tg γ = K_{y} / K_{x} = 0,27

, innen

γ = arc tg 0,27 = 15^{\circ}

2. feladat. Soros

R L C

-körre

U = 200 V \cdot sin (628 s^{- 1} \cdot t)

feszültséget kapcsolunk. Az áramerősség

I = 7,07 A \cdot sin (628 s^{- 1} \cdot t - π / 4)

függvény szerint változik. Az önindukciós együttható

L = 143

mH.
a) Határozzuk meg

R

és

C

értékét!
b) Határozzuk meg a tekercsen és a kondenzátoron a feszültség‐idő függvényeket!

(Blészer Jenő)

Megoldás. a) Mivel az áram késik a feszültséghez képest, a kör induktív jellegű. A fáziskésés nagysága

φ = π / 4 rad = 45^{\circ}

. Az impedancia:

\begin{matrix} Z = \frac{U_{eff}}{I_{eff}} = \frac{U_{max}}{I_{{max}_{}^{}}} = \frac{200 V}{7,07 A} = 28,3 Ω . \end{matrix}

Az ohmikus ellenállás:

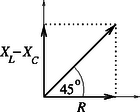
\begin{matrix} R = Z \cdot cos 45^{\circ} = 28,3 Ω \cdot cos 45^{\circ} = 20 Ω . \end{matrix}

A 4. ábrán látható egyenlő szárú derékszögű háromszögből

X_{L} - X_{C} = R,

vagyis

ω L - 1 / (ω C) = R

. Innen

\begin{matrix} C = \frac{1}{ω (ω L - R)} = 22,8 μ F . \end{matrix}

b) A tekercsen a feszültség maximuma

U_{L max} = I_{{max}_{}^{}} X_{L}

, így a feszültség csúcsértéke a tekercsen:

\begin{matrix} U_{L max} = I_{{max}_{}^{}} \cdot ω L = 7,07 A \cdot 628 s^{- 1} \cdot 0,143 H = 635 V . \end{matrix}

Mivel a tekercs feszültsége a kör

U

feszültségéhez képest

π / 4

szöggel siet, a tekercsen eső feszültség időfüggvénye:

\begin{matrix} U_{L} = 635 V \cdot sin (628 \frac{1}{s} \cdot t + \frac{π}{4}) . \end{matrix}

A kondenzátoron a feszültség maximuma:

\begin{matrix} U_{C max} = I_{{max}_{}^{}} X_{C} = I_{max} \frac{1}{ω C} = 494 V, \end{matrix}

és mivel a kondenzátoron eső feszültség a kapocsfeszültséghez képest

3 π / 4

szöggel késik, a feszültség időfüggvénye:

\begin{matrix} U_{C} = 494 V \cdot sin (628 \frac{1}{s} \cdot t + 3 \frac{π}{4}) . \end{matrix}

3. feladat. A természetben található kálium egy része olyan izotóp (jelölése

^{40} K

), amely radioaktív bomlással argonná alakul. A bomlás felezési ideje

1,2 \cdot 10^{9}

év, ami azt jelenti, hogy ennyi idő alatt csökken a radioaktív magok száma a kezdeti érték felére, kétszer annyi idő alatt a negyedére, háromszor annyi idő alatt a nyolcadára és így tovább

...

Az Apolló-program keretében egy olyan követ hoztak a Holdról a Földre, amely

4,0 g

káliumot tartalmazott, amelynek

0,01 %

-a

^{40} K

izotóp volt. Miközben a követ egy lezárt kályhában felmelegítették, a kőből argon szabadult ki. A kiszabadult argongáz térfogatát

20^{\circ} C

hőmérsékleten,

101,3 kPa

nyomáson

2,4 cm^{3}

-nek találták.
Számítsuk ki ennek alapján, hogy minimálisan milyen öreg lehet a Hold, ha feltételezzük, hogy a radioaktív kálium bomlása során keletkező összes argon a kőben maradt, továbbá más módon nem került argon a kőbe!

(Honyek Gyula)

Megoldás. 4 g kálium majdnem pontosan

0,1

mol, a benne található

^{40}

K mennyisége tehát

n_{(^{40} K)} = 10^{- 5}

mol. Az argon mennyisége a

p V = n R T

gáztörvény alapján:

n_{Ar} \approx 1 \cdot 10^{- 4} mol

. A kezdeti

^{40}

K mennyisége tehát

\begin{matrix} n_{(^{40} K)} (0) = n_{(^{40} K)} (t) + n_{Ar} = 10^{- 5} mol + 10^{- 4} mol = 1,1 \cdot 10^{- 4} mol . \end{matrix}

A bomlástörvény alapján:

\begin{matrix} n_{(^{40} K)} (t) = n_{(^{40} K)} (0) \cdot 2^{- \frac{t}{T_{1 / 2}}} \end{matrix}

Ebből

t = 3,46 \cdot T_{1 / 2} = 4,15 \cdot 10^{9}

év adódik. A Hold tehát több mint 4 milliárd éves.

A II. és a III. kategória (valamennyi gimnazista) feladatai

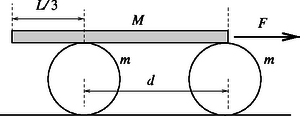
1. feladat. Egy

L = 3 m

hosszúságú,

M = 3 kg

tömegű, homogén tömegeloszlású merev rudat vízszintes asztalon lévő két egyforma, vékonyfalú hengerre fektetünk. A két henger tengelye egymástól

d = 2 m

-re van, továbbá a rúd szélső, ill. a másik végétől számított harmadoló pontja van a hengerek tengelye fölött. A hengerek egyenként

m = 1 kg

tömegűek. A rúdra

F = 12 N

vízszintes irányú, állandó nagyságú húzóerő hat. Mindkét henger csúszásmentesen gördül.
a) Mekkora sebességre gyorsul fel a rúd, miközben a bal oldali vége éppen a bal oldali henger tengelye fölé kerül?
b) Mekkora súrlódási erő és legalább mekkora súrlódási együttható szükséges a tiszta gördüléshez a hengerek és a rúd között?
c) Legalább mekkora a súrlódási együttható az asztal és a hengerek között?

(Zsúdel László)

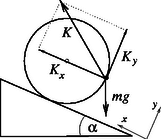
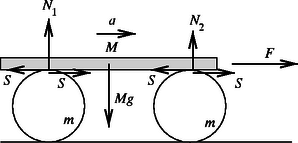
Megoldás. Tekintsük először a vékonyfalú hengereket! A rúdtól származó S súrlódási erő nyilvánvalóan a rúd haladásának irányába mutat. A talajnál ható

F_{s}

súrlódási erőt vegyük fel ugyanebbe az irányba. (Az egyenletrendszer megoldása után

F_{s}

-re kapott előjel eldönti a valódi irányát.)
A hengerek tömegközéppontjára vonatkozó mozgásegyenlet az erők koordinátáival (egy egyenesbe eső vektorok lévén):

S + F_{s} = m a_{s}

, ahol

a_{s}

a henger tömegközéppontjának gyorsulása. A forgatónyomaték-tétel szerint:

(S - F_{s}) r = Θ_{s} β

. A csúszásmentesség kinematikai kényszerfeltétele:

a_{s} = r β

. Ezekből az egytenletekből kifejezhetjük a talaj által kifejtett súrlódási erőt:

\begin{matrix} F_{s} = \frac{m r^{2} - Θ_{s}}{Θ_{s} + m r^{2}} S = 0. \end{matrix}

(Felhasználtuk, hogy a vékonyfalú henger tengelyére vonatkozó tehetetlenségi nyomatéka

Θ_{s} = m r^{2}

.) Az asztal és a hengerek között tehát nem hat súrlódási erő. Ezek szerint a hengerek csúszás nélkül gördülnek akár a tökéletesen sima felületen is!
Térjünk át most a hengerek és a rúd kapcsolatára! A rúd is csúszásmentesen mozog a hengereken (6. ábra), ezért a hengerek legfelső pontjainak sebessége és gyorsulása azonos a rúdéval. Ha viszont a talajon nincs súrlódás, akkor a rúddal érintkező pontokban ható súrlódási erőnek meg kell egyezni mindkét henger esetében, mert csak úgy lehet mindkettőjük gyorsulása azonos. Ez tehát annak ellenére is úgy van, hogy a rúd mozgása közben a rúd és a henger között ható

N_{1}

és

N_{2}

(normál irányú) kényszererők állandóan változnak.

N_{1}

nagysága

M g / 4

-ről indul és maximális értéke

3 M g / 4

a folyamat végén, míg

N_{2}

-re mindez fordítva érvényes:

3 M g / 4

-ről

M g / 4

-re csökken (miközben mindvégig

N_{1} + N_{2} = M g

). Ez természetesen csak úgy teljesülhet, hogy a hengerek és a rúd közötti tapadási súrlódási együttható olyan nagy legyen, hogy a minimális normálerő esetén is biztosítsa az aktuális

S

súrlódási erőt.
A mozgásegyenlet a rúdra:

F - 2 S = M a

. A tömegközéppont mozgásának tétele bármelyik hengerre:

a_{s} = S / m

. A mindkét felületen való csúszásmentes gördülés megköveteli, hogy

a_{s} = a / 2

legyen. Így

a / 2 = S / m

, vagyis

2 S = m a

. Ezt a mozgásegyenletbe helyettesítve:

F - m a = M a

, azaz

\begin{matrix} a = \frac{F}{m + M} = 3 {m/s}^{2} illetve S = \frac{m}{2 (m + M)} F = 1,5 N . \end{matrix}

Így a rúd és hengerek közötti minimális súrlódási együtthatóra

\begin{matrix} μ_{min} = \frac{S}{N_{min}} = \frac{4 S}{M g} = 0,2 \end{matrix}

adódik. A rúd végsebessége:

v = \sqrt[]{2 a (2 L / 3)} = 3,46 m/s

2. feladat. A régiek úgy gondolták, hogy a Föld egy nagy, lapos korong. Képzeljük el, hogy a Föld valóban nem

R

sugarú gömb, hanem igen nagy sugarú,

H

vastagságú lapos korong. Mekkora

H

vastagság esetén tapasztalnánk a korong felszínén (a szélétől messze), hogy a gravitációs gyorsulás ugyanakkora, mint amekkorának a gömb alakú Föld felszínén tapasztaljuk? (

R = 6370 km

. A két ,,Föld''-modellben a sűrűségeket tekintsük állandónak és egymással egyenlőnek.)

(Szegedi Ervin)

Megoldás. Ismeretes, hogy az

R

sugarú,

M

tömegű,

ϱ

sűrűségű Föld felületén a gravitációs gyorsulás a következő alakban adható meg:

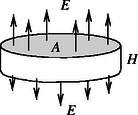
\begin{matrix} g = γ \frac{M}{R^{2}} = γ \frac{ϱ \cdot (4 R^{3} π / 3)}{R^{2}} = \frac{4}{3} γ ϱ R π . \end{matrix}

(1)

A feladat megoldásához meg kell határoznunk egy

H

vastagságú, igen nagy sugarú,

ϱ_{m}

sűrűségű korong fedőlapján a gravitációs gyorsulás nagyságát (távol a korong szélétől). Viszonylag könnyen célt érhetünk, ha kihasználjuk az elektrosztatikus és gravitációs kölcsönhatás erőtörvénye közötti analógiát.
Pontszerű, nyugvó elektromos töltésekre ható elektrosztatikus erő, illetve a pontszerű testek között ható gravitációs erőhatás erőtörvényei azonos jellegűek:

\begin{matrix} F = - γ \frac{m_{1} m_{2}}{r^{3}} \cdot r, illetve F = k \frac{q_{1} q_{2}}{r^{3}} \cdot r, \end{matrix}

ahol

k = 1 / (4 π ε_{0})

. Látható, hogy az

m

tömegnek (,,gravitációs töltésnek'') a

q

elektromos töltés, a

γ

gravitációs állandónak az

1 / (4 π ε_{0})

és a

g = F / m

gravitációs gyorsulásnak az

E = F / q

elektromos térerősség felel meg. Ha tehát meghatároztuk egy homogén töltéssűrűségű, nagyon nagy sugarú korong elektromos térerősségét a korongon kívül, a megfelelő mennyiségek helyettesítésével a gravitációs gyorsulást is megkapjuk a hasonló geometriával bíró tömegeloszlás esetén.
Az elektromos megfelelőt Gauss tétele alapján határozhatjuk meg:

N_{E} = (1 / ε_{0}) \sum q

, ahol az elektromos ,,forráserősség'' a 7. ábrán látható elrendezésben

N_{E} = 2 A E

. Ha az elektromos töltéssűrűség

ϱ_{q}

, akkor a zárt mérőfelület által körülölelt összes töltés

\sum q = ϱ_{q} A H

, tehát

2 E A = \frac{1}{ε_{0}} ϱ_{q} A H

, ahonnan az elektromos térerősség

\begin{matrix} E = \frac{1}{ε_{0}} \frac{ϱ_{q} H}{2} . \end{matrix}

(2)

A gravitációs gyorsulás tehát az egymásnak megfelelő mennyiségek átírásával (2)-ből:

\begin{matrix} g = 4 π γ \frac{ϱ_{m} H}{2} . \end{matrix}

Ennek kell a homogénnek tekintett Föld felszínén mérhető gravitációs gyorsulással megegyeznie, amely (1) alapján:

\begin{matrix} g_{gömb} = g_{korong} = γ \frac{4 R π ϱ_{m}}{3} = 4 π γ \frac{ϱ_{m} H}{2}, \end{matrix}

ahonnan a ,,lapos Föld'' korongjának vastagsága:

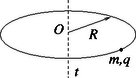
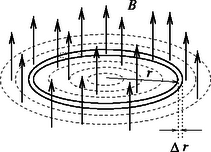
\begin{matrix} H = \frac{2}{3} R = \frac{2}{3} \cdot 6370 km = 4250 km . \end{matrix}

3. feladat. Egy

m

tömegű,

q

töltésű kicsiny gyöngyöt

R

sugarú, szigetelő anyagból készült, vízszintes síkú, vékony karikára fűzünk. A körpályán a gyöngy súrlódás nélkül mozoghat és kezdetben nyugalomban van. Ezután olyan (a

t

tengelyre) hengerszimmetrikus mágneses mezőt hozunk létre, amelyben a mágneses indukció pályasíkra merőleges komponense csak a középponttól mért

r

távolságtól és a

t

időtől függ:

B (r, t) = E_{0} \cdot t / r

, ahol

E_{0}

adott konstans. (Az

r = 0

elhanyagolható kiterjedésű környezetében az indukció valamilyen véges érték.)
a) Határozzuk meg a gyöngy sebesség‐idő függvényét!
b) Hogyan alakul a gyöngy és a pálya között ható nyomóerő sugárirányú komponense az idő függvényében?

(Szegedi Ervin)

Megoldás. a) Határozzuk meg a körpálya által körülvett fluxust az idő függvényében! Mivel az indukció a sugár mentén változik, olyan kis tartományokra osztjuk a körterületet, amelyeken belül a mágneses mező homogénnek vehető (9. ábra).
Jelöljünk ki ezért egy

r

sugarú,

Δ r ≪ r

szélességű körgyűrűt, amelynek fluxusa:

Δ Φ = = B (r, t) \cdot 2 r π \cdot Δ r

. A feladat követelménye szerint

Δ Φ = \frac{E_{0}}{r} t \cdot 2 r π \cdot Δ r

. Összegezzük az elemi fluxust:

\begin{matrix} Φ (t) = \sum Δ Φ = 2 π E_{0} t \sum_{i}^{} Δ r_{i} = 2 π E_{0} t R, \end{matrix}

azaz

Φ (t) = 2 π E_{0} R t

.
A hengerszimmetria miatt a kialakuló indukált elektromos mező is hengerszimmetrikus, és így térerőssége a gyöngy helyén:

\begin{matrix} E (R) = \frac{1}{2 π R} \frac{Δ Φ}{Δ t} = \frac{1}{2 π R} \cdot \frac{2 π R E_{0} Δ t}{Δ t} = E_{0} . \end{matrix}

A gyöngyre érintő irányban állandó nagyságú elektromos erő hat, tehát sebessége az idő függvényében:

v (t) = \frac{E_{0} q}{m} \cdot t

b) Sugár irányban alkalmazva a mozgásegyenletet:

q v B + N = m v^{2} / R

, ahol

N

a pálya által kifejtett kényszererő. Ennek nagysága

v (t)

fentebb kiszámított kifejezésének felhasználásával:

\begin{matrix} N = q v B - m \frac{v^{2}}{R} = q \cdot \frac{E_{0} q}{m} t \cdot \frac{E_{0} t}{R} - \frac{m}{R} \frac{E_{0}^{2} q^{2} t^{2}}{m^{2}} = 0. \end{matrix}

A gyöngyszem és a karika között tehát nem hat erő az ilyen szerkezetű mágneses mezőben. Mivel a pálya nem fejt ki sugárirányú nyomóerőt, akár ott sem kell lennie! Ez a betatron részecskegyorsító elve.

A fizika I. kategória végeredménye

1. Guti Lajos (Budapest, Puskás Tivadar Távközlési Technikum, III. o.t.),
tanára: Beregszászi Zoltán;
2. Prókai Tibor (Szeged, Déri Miksa Ip. Szki., IV. o.t.),
tanára: Horváth László;
3. Vörös Sándor (Paks, Energetikai Szakképzési Int., III. o.t.),
tanára: Árokszállási Tibor;

4. Simon Kornél (Miskolc, Andrássy Gy. Műsz. Szki., IV. o.t.), tanára: Dobos Zsolt; 5. Erdei Zoltán (Bp., Bolyai J. Műsz. Szki., IV. o.t.), tanára: Jakab Emese; 6. Molnár Zsolt (Paks, Energetikai Szakképzési Int., IV. o.t.), tanára: Csajági Sándor; 7. Kiss Béla (Vác, Boronkay Gy. Műsz. Szki., IV. o.t.), tanára: Arany Tóth László; 8. Pap Gábor (Bp., Trefort Á. Műsz. Szki., III. o.t.), tanára: Pecsenye Sándor; 9. Dányádi Attila (Kaposvár, Eötvös L. Műsz. Szki., III. o.t.), tanára: Sárdi Zoltán; 10. Pribelszki János (Bp., Puskás T. Távk. Techn., IV. o.t.), tanára: Nagy Józsefné; 11. Mészáros Balázs (Paks, Energetikai Szakképzési Int., IV. o.t.); 12. Sebestyén Balázs (Bp., Újpesti Műsz. Szki., IV. o.t.); 13. Brezniczky János (Eger, Gép- és Műszerip. Szki., III. o.t.); 14. Mikó Péter (Debrecen, Gábor D. Műszaki Középisk., IV. o.t.); 15. Szabadi Péter (Paks, Energetikai Szakképzési Int., IV. o.t.); 16. Jurácz László (Vác, Boronkay Gy. Műsz. Szki., IV. o.t.).

A fizika II. kategória végeredménye

1. Tóth Gábor Zsolt (Budapest, Árpád Gimn., IV. o.t.),
tanára: Vankó Péter;
2. Várkonyi Péter (Fazekas M. Főv. Gyak. Gimn., III. o.t.),
tanára: Horváth Gábor;
3. Böde Csaba (Nagykanizsa, Batthyány Lajos Gimn., IV. o.t.),
tanára: Soós Sándor;

4. Kovács Baldvin (Fazekas M. Főv. Gyak. Gimn., IV. o.t.), tanára: Horváth Gábor; 5. Vörös Zoltán (Tiszavasvári, Váci M. Gimn., IV. o.t.), tanárai: Víg Csaba, dr. Szegedi Ervin; 6. Perényi Márton (Fazekas M. Főv. Gyak. Gimn., IV. o.t.), tanára: Horváth Gábor; 7. Hegyi Barnabás (Zalaegerszeg, Zrínyi M. Gimn., IV. o.t.), tanára: Orbán Edit; 8. Tóth Péter (Miskolc, Földes F. Gimn., IV. o.t.), tanára: Zámborszky Ferenc; 9. Bárász Mihály (Fazekas M. Főv. Gyak. Gimn., IV. o.t.), tanára: Horváth Gábor; 10. Elek Péter (Budapest, Árpád Gimn., IV. o.t.), tanára: Vankó Péter; 11. Király Csaba (Fazekas M. Főv. Gyak. Gimn., IV. o.t.); 12. Braun Gábor (Bp., Szent István Gimn., IV. o.t.); 13. Göller Ákos (Fazekas M. Főv. Gyak. Gimn., IV. o.t.); 14. Frenkel Péter (Fazekas M. Főv. Gyak. Gimn., III. o.t.); 15. Burcsi Péter (Pápa, Türr I. Gimn., IV. o.t.); 16. Gyukics Mihály (Szolnok, Varga K. Gimn., IV. o.t.); 17. Péli Gergely (Fazekas M. Főv. Gyak. Gimn., IV. o.t.); 18. Wagner Róbert (Pannonhalma, Bencés Gimn., IV. o.t.); 19. Koncz Imre (Fazekas M. Főv. Gyak. Gimn., III. o.t.); 20. Laczkó Gábor (Pécs, Janus Pannonius Gimn., IV. o.t.); 21. Hegedűs Márton (Fazekas M. Főv. Gyak. Gimn., IV. o.t.); 22. Várszegi Zsolt (Zalaegerszeg, Ságvári E. Gimn., III. o.t.); 23. Varró Gergely (Fazekas M. Főv. Gyak. Gimn., III. o.t.); 24. Mátrai Tamás (Fazekas M. Főv. Gyak. Gimn., III. o.t.).

A fizika III. kategória végeredménye

1. Lovas Rezső (Debrecen, KLTE Gyak. Gimn., IV. o.t.),
tanárai: Dudics Pál, dr. Kirsch Éva, dr. Szegedi Ervin;
2. Lestyán Zsolt (Kecskemét, Katona József Gimn., IV. o.t.),
tanára: dr. Szablics Bálint;
3. Várnagy Gábor (Budapest, ELTE Apáczai Csere János Gyak. Gimn., IV. o.t.),
tanára: Flórik György;

4. Véber Miklós (Veszprém, Lovassy L. Gimn., IV. o.t.), tanára: Schultz Zoltán; 5. Pongrácz Gergely (Mosonmagyaróvár, Kossuth L. Gimn., IV. o.t.), tanárai: Horváth László, Sipőcz István; 6. Fabó Márton (Bp., Berzsenyi D. Gimn., III. o.t.), tanára: Gyenes Gábor; 7. Holcsek Balázs (Veszprém, Lovassy L. Gimn., IV. o.t.), tanára: Király László; 8. Kurucz Zoltán (Szolnok, Varga K. Gimn., IV. o.t.), tanára: Vincze Gábor; 9. Fábián Zoltán (Kecskemét, Katona József Gimn., IV. o.t.), tanára: dr. Szablics Bálint; 10. Agod Attila (Debrecen, Tóth Á. Gimn., IV. o.t.), tanára: Kovács Miklós; 11. Volk János (Bp., ELTE Radnóti M. Gyak. Gimn., IV. o.t.); 12. Gubás Lóránd (Miskolc, Földes F. Gimn., III. o.t.); 13. Gombkötő Ákos (Bp., ELTE Radnóti M. Gyak. Gimn., IV. o.t.); 14. Rácz Attila (Debrecen, KLTE Gyak. Gimn., IV. o.t.); 15. Payrits Szabolcs (Sopron, Széchenyi I. Gimn., IV. o.t.); 16. Szabó Gábor (Veszprém, Lovassy L. Gimn., IV. o.t.); 17. Pályi Balázs (Szeged, JATE Ságvári E. Gyak. Gimn., IV. o.t.); 18. Nős Bálint (Pécs, Széchenyi I. Gimn., IV. o.t.); 19. Vágvölgyi Attila (Bp., ELTE Radnóti M. Gyak. Gimn., IV. o.t.); 20. Bartal Balázs (Pécs, JPTE Babits M. Gyak. Gimn., IV. o.t.).

Holics László

^{$^{*}$}*