Kezdőlap


Cím:	Néhány kombinatorikus geometriai feladat
Szerző(k):	Bogdán Zoltán
Füzet:	1997/december, 514 - 519. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

¹
Az alábbi problémák megoldásához analízisből vett eszközöket használunk. Ezek a feladatok középiskolás diákok számára is hozzáférhetőek, és jelentősen mélyíthetik a függvény és a folytonosság fogalmát.

1. Bizonyítsuk be, hogy bármely korlátos, konvex síkbeli alakzat adott irányú egyenessel két egyenlő területű részre vágható szét.

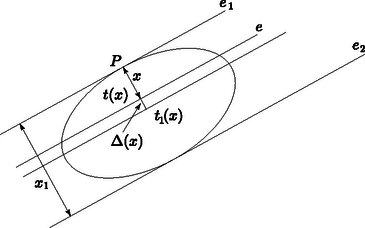
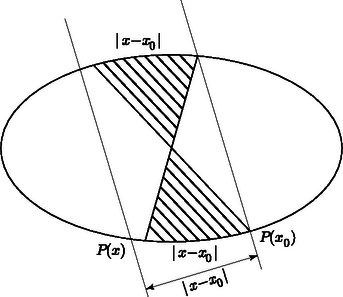
Megoldás. Az 1. ábrán

e

az adott iránnyal párhuzamos egyenes,

e_{1}

és

e_{2}

pedig ugyanilyen irányú támaszegyenesek. Legyen

P

e_{1}

egyenes és a konvex alakzat közös pontja,

P

és

e

távolságát pedig jelöljük

x

-szel. Az

e

egyenes az alakzatot két részre vágja, legyen a két rész területe az ábra szerint

t (x)

és

t_{1} (x)

. Feltehetjük, hogy

t (x) < t_{1} (x)

, azaz

t (x) - t_{1} (x) < 0

. Ha

e_{1}

és

e_{2}

távolsága

x_{1}

, akkor nyilván

t (x_{1}) - t_{1} (x_{1}) > 0

. Ezért, ha

t (x)

és

t_{1} (x)

x

-nek folytonos függvényei, akkor Bolzano tétele² szerint az

(x; x_{1})

intervallumban van olyan

x_{0}

, amelyre

t (x_{0}) - t_{1} (x_{0}) = 0

, ami a feladat állítását jelenti. Megmutatjuk, hogy

t (x)

(és

t_{1} (x)

) folytonos függvénye

x

-nek.

Ehhez definíció szerint azt kell belátnunk, hogy tetszőleges

ε

pozitív számhoz található olyan

δ > 0

, hogy minden

Δ x < δ

esetén

| t (x + Δ x) - t (x) | < ε

. A korlátosság feltétele szerint létezik olyan

R

sugarú kör, amely a konvex alakzatot magába foglalja. Ezért

\begin{matrix} | t (x + Δ x) - t (x) | \leq 2 R Δ x < 2 R δ < ε, \end{matrix}

δ = \frac{ε}{2 R}

Feladat. Bizonyítandó, hogy a feladat állítása adott irányú egyenes helyett adott ponton átmenő egyenessel is érvényes.

2. Bizonyítsuk be, hogy minden korlátos, konvex síkbeli tartományhoz létezik két egymásra merőleges egyenes, amelyek a tartományt négy egyenlő területű részre vágják.

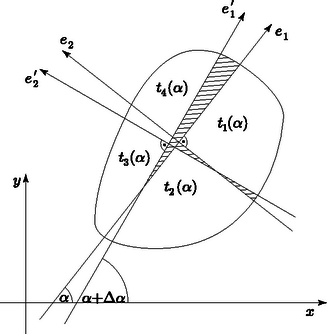
Megoldás. Legyenek

e_{1}

és

e_{2}

a konvex halmaz területét felező egymásra merőleges (irányított) egyenesek. Ilyenek az előző feladat szerint léteznek. Jelöljük az

e_{1}

és az

x

tengely szögét

α

-val, az

e_{1}

és

e_{2}

létrehozta négy síkrész területét

t_{i} (α)

-val, és használjuk a 2. ábra további jelöléseit is. Tekintve, hogy

t_{1} (α) + t_{2} (α)

, valamint

t_{2} (α) + t_{3} (α)

is a konvex alakzat területének a fele,

t_{1} (α) = t_{3} (α)

, és hasonlóan

t_{2} (α) = t_{4} (α)

. Ezért a feladat állításának igazolásához elegendő megmutatni, hogy van olyan

α_{0}

szög, amellyel

t_{1} (α_{0}) = t_{2} (α_{0})

. Ha

α

már ilyen, akkor készen vagyunk. Egyéb esetben feltehetjük, hogy

t_{1} (α) > t_{2} (α)

, azaz

t_{1} (α) - t_{2} (α) > 0

. Forgassuk el

e_{1}

-et és

e_{2}

-t

90^{\circ}

-kal úgy, hogy eközben mindig területfelező egyenesek maradjanak.

Ekkor

t_{1} (α + 90^{\circ}) = t_{4} (α)

t_{2} (α + 90^{\circ}) = t_{1} (α)

, és így

\begin{matrix} t_{1} (α + 90^{\circ}) - t_{2} (α + 90^{\circ}) = t_{2} (α) - t_{1} (α) < 0. \end{matrix}

Azt nyertük, hogy a

t_{1} (α) - t_{2} (α)

függvény az

[α; α + 90^{\circ}]

intervallumban előjelet vált. Ezért, feltéve, hogy

t_{1} (α)

és

t_{2} (α)

folytonos, Bolzano tétele szerint létezik olyan

α_{0}

, amellyel

t_{1} (α_{0}) = t_{2} (α_{0})

. Forgassuk el

e_{1}

-et és

e_{2}

-t egy

Δ α

szöggel. Az elforgatott egyenesek

e_{1}'

és

e_{2}'

, Megmutatjuk, hogy pl.

t_{1} (α)

folytonos. Ehhez meg kell becsülnünk

t_{1} (α + Δ α)

és

t_{1} (α)

különbségét. Az ábrán bevonalkázott területek mindegyike kisebb

\frac{{(2 R)}^{2} \cdot Δ α}{2}

-nél, ahol

R

egy olyan kör sugara, amely magába foglalja a konvex alakzatot. Ilyen kör a korlátosság következtében létezik. Könnyen belátható, hogy

\begin{matrix} | t_{1} (α + Δ α) - t_{1} (α) | < 4 \frac{(2 R^{2}) \cdot Δ α}{2} < ε, ha Δ α < \frac{ε}{8 R^{2}} < δ, ahol ε > 0. \end{matrix}

3. Bizonyítsuk be, hogy bármely korlátos síkbeli ponthalmaz belefoglalható egy négyzetbe úgy, hogy a négyzet mindegyik oldalán van az alakzat határának pontja.

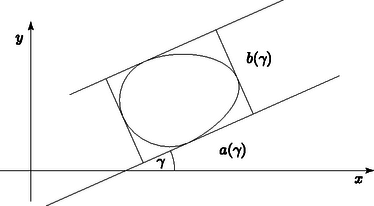
Megoldás. Először konvex tartományokra bizonyítjuk az állítást. Legyenek a konvex alakzat támasztéglalapjának oldalai

a (γ)

b (γ)

, ahol

γ

a

oldal egyenesének az

x

tengellyel bezárt szöge (3. ábra).

Itt fölhasználjuk azt a tényt, hogy korlátos síkbeli ponthalmaz belefoglalható két adott irányú támaszegyenes közötti sávba. Ha

a (γ) = b (γ)

, akkor a feladat állítása igaz. Tegyük fel ezután, hogy

a (γ) > b (γ)

, azaz

a (γ) - b (γ) > 0

. Tekintsük a

γ + 90^{\circ}

szöghöz tartozó támasztéglalap oldalait:

\begin{matrix} a (γ + 90^{\circ}) = b (γ); b (γ + 90^{\circ}) = a (γ) . \end{matrix}

Ezekből

\begin{matrix} a (γ + 90^{\circ}) - b (γ + 90^{\circ}) = b (γ) - a (γ) < 0. \end{matrix}

Ezért, ha

a (γ)

és

b (γ)

folytonos, akkor Bolzano tétele szerint a

[γ; γ + 90^{\circ}]

intervallumban létezik olyan

γ_{0}

hely, amelyre

a (γ_{0}) - b (γ_{0}) = 0

, tehát a támasztótéglalap négyzet.
Ha a ponthalmaz nem konvex, akkor konvex burkára létezik körülírt négyzet. Mivel egy alakzat konvex burka éppen a támaszegyenesei által meghatározott félsíkok közös része, a konvex burok minden támaszegyenese az eredeti alakzatnak is támaszegyenese. Ezért a konvex burok körülírt négyzete az eredeti alakzatnak is körülírt négyzete.

Feladat. Mutassuk meg, hogy

a (γ)

és

b (γ)

γ

-nak folytonos függvénye.

4. Bizonyítandó, hogy a sík bármely korlátos, konvex halmazához található olyan egyenes, amely a konvex alakzat területét és határvonalát is felezi.

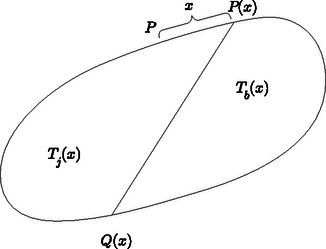
Megoldás. Legyen a halmaz határvonalának hossza

k

. Legyen

P (x)

az a pont, amelyre rögzített

P

és

P (x)

közötti kisebbik kerület darab hossza

x

, ahol

0 \leq x \leq \frac{k}{2}

. Legyen a

P (x)

-szel szemben levő pont

Q (x)

, ami azt jelenti, hogy a két pontot összekötő (irányított) egyenes a konvex halmaz határvonalát két egyenlő hosszú részre vágja. Ennek az egyenesnek a ,,jobb'' oldalán lévő területrész legyen

T_{j} (x)

, a másik

T_{b} (x)

(4. ábra). Ha

T_{j} (x) = T_{b} (x)

, akkor a feladat állítása igaz. Egyébként feltehető, hogy pl.

T_{j} (0) - T_{b} (0) > 0

Mivel

\begin{matrix} T_{j} (\frac{k}{2}) = T_{b} (0) és T_{b} (\frac{k}{2}) = T_{j} (0), \end{matrix}

azért

\begin{matrix} T_{j} (\frac{k}{2}) - T_{b} (\frac{k}{2}) = T_{b} (0) - T_{j} (0) < 0. \end{matrix}

Így, ha

T_{j} (x)

és

T_{b} (x)

x

-nek folytonos függvényei, akkor Bolzano tétele szerint létezik olyan

x_{0}

, amelyre

T_{j} (x_{0}) - T_{b} (x_{0}) = 0

. Az

x_{0}

-hoz tartozó

P (x_{0})

és

Q (x_{0})

pontokat összekötő egyenes a konvex alakzat területét és kerületét is felezi.

Be kell még bizonyítanunk, hogy

T_{j} (x)

(és

T_{b} (x)

is)

x

-nek folytonos függvénye. Használjuk az 5. ábra jelöléseit. A

P (x)

P (x_{0})

pontok és a velük szemköztiek belefoglalhatók egy

| x - x_{0} |

szélességű és

2 R

hosszúságú téglalapba, ahol

| x - x_{0} |

P (x)

és

P (x_{0})

közötti kerület darab hossza,

R

pedig egy a konvex halmazt magába foglaló kör sugara. Mivel

T_{j} (x)

megváltozása a bevonalkázott területek különbségeinek abszolút értéke, érvényes a következő becslés:

\begin{matrix} | T_{j} (x) - T_{j} (x_{0}) | < | x - x_{0} | \cdot 2 R < ε, \end{matrix}

| x - x_{0} | < \frac{ε}{2 R} = δ

, ahol

ε > 0

. Tehát

T_{j} (x)

valóban folytonos.

Megjegyzés. Ebben a feladatban ‐ és az előbbiekben is ‐ fölhasználtuk, hogy korlátos, konvex síkbeli alakzatnak van területe. Az 1. feladatban a konvexség feltétele csak a terület létezése miatt kellett. Ebben a feladatban fölhasználtuk azt is, hogy korlátos és zárt, konvex síkbeli alakzat határvonala mérhető.

5. Van-e olyan sík, amely egy adott tetraédert két egyenlő felszínű és térfogatú részre vág szét?

1. megoldás. Először bebizonyítjuk, hogy a tetraéder két szemközti élének felezőpontján átmenő sík felezi a tetraéder térfogatát. Két esetet különböztetünk meg.
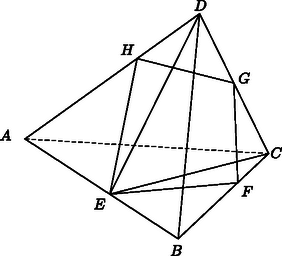
a) Legyen az

A B C D

tetraéder

A B

élének felezőpontja

E

, a

C D

él felezőpontja pedig

G

(6. ábra). Az

E

és

G

pontokon átmenő

C E D

sík a tetraédert két egyenlő térfogatú részre vágja. Ugyanis a

C E

súlyvonal felezi az

A B C

háromszög területét, ezért az

A E C D

és

E B C D

tetraéderek

A E C

és

E B C

alapterülete megegyezik, továbbá egybeesik a

D

-ből húzható magasságuk is.

b) Forgassuk el a

C E D

síkot az

E G

egyenes körül. Az elforgatott sík a tetraédert az

E F G H

négyszögben metszi. Azt állítjuk, hogy az elforgatott sík is felezi a tetraéder térfogatát. Tekintsük az

E B C D

tetraédert. Ebből az elforgatott sík egyrészt levágja az

E F G

alapú

C

csúcsú gúlát, másrészt hozzáveszi az

E G H

alapú

D

csúcsú gúlát. Mivel a tetraéder

A D

és

B C

éle egy-egy

E G

-vel párhuzamos síkba foglalható, az

F

és

H

pontok egyenlő távolságra vannak

E G

-től. Ezért az

E F G

és az

E G H

háromszögek területe egyenlő. Tekintve, hogy a

G

pont a

C D

él felezőpontja, a

C

és

D

pontoknak az

E F G H

síktól való távolsága ugyanakkora, ezért az említett két gúla magassága is egyenlő, tehát térfogatuk egyenlő. Ez azt jelenti, hogy az elforgatott sík felezi a tetraéder térfogatát. A

C E D

sík

G E

körüli forgatása közben pl. az

F

pont a

D A

szakaszon mozog

A

felé. Ha

F

egybeesik

A

-val, újra előáll a megoldás a) részében leírt helyzet. Ha az

A B G

síkot

E G

körül tovább forgatjuk, a megoldás b) részében leírtak ismétlődnek.
Tekintsünk ezután egy, a tetraéder térfogatát felező

S

síkot. A két résztest felszíne ‐ a metszetlap területe nélkül ‐ legyen

A_{1} (γ)

, illetve

A_{2} (γ)

, ahol

γ

S

-nek és egy rögzített síknak a hajlásszöge. Ha

A_{1} (γ) = A_{2} (γ)

, akkor készen vagyunk. Tegyük fel ezután, hogy

A_{1} (γ) > A_{2} (γ)

, azaz

A_{1} (γ) - A_{2} (γ) > 0

. Forgassuk el

S

-et a tetraéder két szemközti élének felezőpontját összekötő egyenes körül

180^{\circ}

-kal. Ekkor

A_{1} (γ + 180^{\circ}) = A_{2} (γ)

és

A_{2} (γ + 180^{\circ}) = A_{1} (γ)

, hiszen az

S

sík

180^{\circ}

-os forgatás után önmagába megy át. Ezért

\begin{matrix} A_{1} (γ + 180^{\circ}) - A_{2} (γ + 180^{\circ}) = A_{2} (γ) - A_{1} (γ) < 0. \end{matrix}

Feltéve, hogy

A_{1} (γ) - A_{2} (γ)

folytonos, Bolzano tétele szerint lesz a

[0^{\circ}; 180^{\circ}]

intervallumban olyan

γ_{0}

szög, amelyre

A_{1} (γ_{0}) - A_{2} (γ_{0}) = 0

, tehát

A_{1} (γ_{0}) = A_{2} (γ_{0})

Feladat. Bizonyítsuk be, hogy

A_{1} (γ)

és

A_{2} (γ)

γ

-nak folytonos függvényei.

2. megoldás. A feladat elemi úton is megoldható. Az elemi megoldásnak további szépsége, hogy megad egy olyan síkot, amely a tetraéder felszínét és térfogatát is felezi, míg az első megoldásban csak létezést bizonyítottunk.
Legyen a

V

térfogatú,

A

felszínű tetraéder beírt gömbjének középpontja

O

. Az

O

pontot a csúcsokkal összekötve a tetraédert olyan gúlákra bonthatjuk, amelyek alapterülete a tetraéder egy-egy lapja, magassága pedig a beírt gömb

r

sugara. Ezeknek a gúláknak a térfogatát összeadva a tetraéder térfogatát kapjuk. Ezért

V = \frac{A \cdot r}{3}

. Vegyünk fel ezután egy

O

-n átmenő tetszőleges síkot. Ez a sík a tetraédert egy

V_{1}

, illetve

V_{2}

térfogatú részre vágja, legyen a

V_{1}

térfogatú testhez tartozó felszínrész

A_{1}

, a másik

A_{2}

. A szóban forgó sík az előbb említett gúlák némelyikét nem metszi, másokat pedig két

O

csúcsú gúlára vág szét, ezért

V_{1} = \frac{A_{1} \cdot r}{3}

és

V_{2} = \frac{A_{2} \cdot r}{3}

.
Az 1. megoldásban bebizonyítottuk, hogy a tetraéder két szemközti élének felezőpontján átmenő sík felezi a tetraéder térfogatát. Tekintsük azt a síkot, amely két szemközti él felezőpontján és az

O

ponton megy át. Ez a sík felezi a tetraéder térfogatát, azaz

V_{1} = V_{2}

, ezért az előbbi képletekből

A_{1} = A_{2}

6. Bizonyítsuk be, hogy a tér bármely korlátos, konvex halmazához található olyan sík, amely a test térfogatát és felszínét is felezi.

Megoldás. A feladat megoldását az Olvasóra bízzuk. Mutassuk meg, hogy a tér egy adott egyenesén átmenő síkok bármelyikéhez található vele párhuzamos sík, amely a korlátos, konvex halmazt két egyenlő térfogatú részre vágja. Egy ilyen sík és a

180^{\circ}

-os elforgatottja egybeesik. (Mindig csak olyan síkokat tekintünk, amelyek az adott egyenesre illeszkedő síksor valamelyik elemével párhuzamosak.) A

[0^{\circ}; 180^{\circ}]

intervallumban lesz olyan szög, amellyel egy, a térfogatot felező síkot elforgatva, az elforgatott sík a felszínt is felezi. Végül meg kell mutatni, hogy a felszín a forgatás szögének folytonos függvénye.

Bogdán Zoltán

¹A cikk megjelent a Polygon folyóirat 1992. májusi számában (115‐123. o.)

²E tétel a következőt állítja: ha $f$ az $[a, b]$ intervallumon folytonos függvény, akkor ott $f$ minden $f (a)$ és $f (b)$ közötti valós értéket felvesz.