Cím:	Az 1996-97. évi Arany Dániel Matematikai Tanulóverseny feladatai, eredményei
Füzet:	1997/november, 452 - 460. oldal	PDF  |  MathML
Témakör(ök):	Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   KEZDŐK Első forduló   1. Határozza meg azokat a valós számpárokat, amelyekre teljesül az alábbi egyenlet: $\begin{array}{c}{\displaystyle x^4+6x^3+\left|y^2-x^2\right|+9x^2=0.}\end{array}$   2. Egységnyi élű kockákból egységnyi alapélű négyzetes oszlopokat készítünk, melyeknek a felszíne egy egységnyi élű kocka felszínének egész számú többszöröse. Hányféle ilyen négyzetes oszlop készíthető, ha legfeljebb $1997$ darab egységnyi élű kocka áll rendelkezésünkre egy négyzetes oszlop előállításához?   3. Az $ABC$ háromszögben a $C$ csúcsnál tompaszög van. A háromszög $AB$ oldalához hozzáírt kör az $AC$ egyenest $M$, a $BC$ egyenest $N$ pontban érinti. Bizonyítsa be, hogy $\begin{array}{c}{\displaystyle \frac{1}{3}\left(CM+CN\right)<AB<\frac{1}{2}\left(CM+CN\right)\mathrm{.}}\end{array}$   4. A $p$ valós paraméter mely értékei esetén van a valós számok halmazán pontosan egy megoldása az alábbi egyenletnek? $\begin{array}{c}{\displaystyle |x+2|-p|x-1|=4}\end{array}$   5. Az $n$ és $k$ pozitív egészekről azt tudjuk, hogy $n$ páratlan, $k\ge 8$, az $n$ (tízes számrendszerben) $k$ jegyű, az $n-1$ osztható $10001$-gyel, továbbá $n$ számjegyeinek összege $6k+3$, $\frac{n-1}{10001}$ számjegyeinek összege $3k+1$, végül $\frac{n-1}{10001}$-ben található $k-6$ darab megegyező, egymásutáni páratlan számjegy. Mi lehet a $k$?   Második forduló 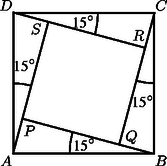 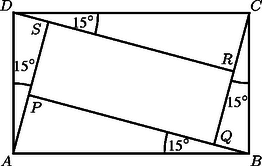     I kategória: Szakközépiskolások       1. Az $ABCD$ négyzet oldala $10$ cm. Bizonyítsa be, hogy a $PQRS$ négyszög négyzet, és a négyzetek területeire fennáll a következő egyenlőtlenség: $\begin{array}{c}{\displaystyle 2\cdot T_{PQRS}=T_{ABCD}\mathrm{.}}\end{array}$   2. Oldja meg a valós számok halmazán a következő egyenletet: $\begin{array}{c}{\displaystyle \left[x\right]=\frac{8}{7}x-\frac{3}{7}\mathrm{,}}\end{array}$ ahol $\left[x\right]$ az $x$ szám egész részét jelenti.   3. Oldja meg az egész számpárok halmazán az alábbi egyenletet: $\begin{array}{c}{\displaystyle x^3-y^3=91.}\end{array}$     II. kategória: Nem speciális matematika tantervű gimnáziumi tanulók       1. Oldja meg az egész számpárok halmazán az alábbi egyenletet:  $x^3-y^3=91$.   2. Az $ABCD$ téglalap két szomszédos oldala $30$ cm és $50$ cm. Bizonyítsa be, hogy az $ABCD$ téglalap és a $PQRS$ négyszög területeire fennáll a következő egyenlőtlenség: $\begin{array}{c}{\displaystyle 30\cdot T_{PQRS}=17\cdot T_{ABCD}\mathrm{.}}\end{array}$   3. A tízes számrendszerben hány olyan $6$-tal osztható $n$ jegyű szám ($n\in {\text{N}}^{+}$ és $n>2$) van, amelyre teljesül, hogy a számjegyeinek összege megegyezik azzal az $\left(n-1\right)$ jegyű számmal, amelyet belőle a legmagasabb helyiértékű helyen álló számjegyének elhagyásával kapunk?     III. kategória: Speciális matematika tantervű gimnáziumi tanulók       1. Igaz-e, hogy bármely $b$ és $c$ valós számhoz található olyan $K$ pozitív valós szám, hogy minden $K$-nél nagyobb $a$ és $x$ valós szám esetén teljesül a következő egyenlőtlenség: $\begin{array}{c}{\displaystyle a{x}^2+bx+c>0.}\end{array}$   2. Az $ABC$ háromszögben $CA=CB$. Vegyen fel a háromszög köré írható kör $BC$ ívén egy tetszőleges $P$ pontot, és legyen a $C$-ből az $AP$-re bocsátott merőleges talppontja $T$. Igazolja, hogy $\begin{array}{c}{\displaystyle \overline{AT}=\overline{TP}+\overline{PB}\mathrm{.}}\end{array}$   3. Legyen $\begin{array}{c}{\displaystyle c_n:={\left(1+\frac{1}{n}\right)}^n\left(1+\frac{1}{4n}\right)\mathrm{,}n\in {\text{N}}^{+}\mathrm{.}}\end{array}$ Bizonyítsa be, hogy $c_n<c_{n+1}$, $n\in {\text{N}}^{+}$.   HALADÓK Első forduló       I. és II. kategória: Szakközépiskolások és nem speciális tantervű gimnáziumi tanulók       1. A $p$ paraméter mely értéke esetén van a $\begin{array}{c}{\displaystyle \sqrt[]{x-\sqrt[]{x-p}}=\sqrt[]{p+\sqrt[]{x-p}}}\end{array}$ egyenletnek pontosan egy gyöke az egész számok halmazán?   2. Az $A$, illetve $B$ középpontú kör kívülről érinti egymást az $E$ pontban. Egyik közös külső érintőszakaszuk felezőpontja az $F$ pont. Az $FA$ és $FB$ szakasz a két kört a $C$ és $D$ pontban metszi. Bizonyítsuk be, hogy a $CED$ szög nagysága független az érintkező körök sugarának hosszától!   3. Igazoljuk, hogy bármely valós $a$ és $b$ számra teljesül a $8\left(a^4+b^4\right)\ge {\left(a+b\right)}^4$ egyenlőtlenség!   4. Az $ABCD$ négyzet $AB$ oldalának $A$ csúcshoz közelebbi harmadolópontja az $E$ pont, a $DC$ oldal felezőpontja pedig az $F$ pont. A négyzet $AC$ átlóját a $DE$ szakasz az $M$ pontban, a $BF$ szakasz az $N$ pontban metszi. Bizonyítsuk be, hogy az $AEM$ és a $CFN$ háromszögek hasonlóak!   5. Egy téglalap alakú táblázat $8000$ darab mezőt tartalmaz. Kiválasztottuk néhány, de $2$-nél több sorát és $2$-nél több oszlopát. Azt tapasztaltuk, hogy azoknak a mezőknek a száma, amelyeknek sora és oszlopa közül legalább az egyik ki van választva, $1996$. Hány sort és hány oszlopot választottunk ki?         III. kategória: Speciális matematika tantervű gimnáziumi tanulók       1. Oldjuk meg a valós számpárok halmazán az $\begin{array}{c}{\displaystyle \frac{x^2\left(x+1\right)}{y+1}+\frac{y^2\left(y-1\right)}{x-1}=\frac{2}{y+1}-\frac{2}{x-1}}\end{array}$ egyenletet!   2. Mutassuk meg, hogy ha $a$, $b$, $c$ egy háromszög oldalainak hossza, akkor $\begin{array}{c}{\displaystyle 3\le \frac{{\left(a+b+c\right)}^2}{ab+bc+ca}<4.}\end{array}$   3. Az $ABC$ hegyesszögű háromszög köréírt körének középpontja $K$, magasságpontja pedig $M$. Bizonyítsuk be, hogy ha a $BAC$ szög ${60}^{\circ }$-os, akkor az $A$ csúcsból a $KM$ szakaszra állított merőleges felezi a $KM$ szakaszt!   4. Melyik az a legkisebb pozitív egész szám, amely előállítható a) ${81}^x-5^y$, b) $\left|{81}^x-5^y\right|$ alakban, ahol $x$ és $y$ pozitív egész szám?   Második forduló       I. kategória: Szakközépiskolások       1. Mekkora területű alakzatot határoznak meg azok a $P\left(x;y\right)$ koordinátájú pontok, amelyeknek $x$ és $y$ koordinátája kielégíti az $1996\le |x|+|y|\le 1997$ egyenlőtlenségrendszert?   2. Egy $ABC$ derékszögű háromszög $CAB$ szöge ${30}^{\circ }$, $AC=a$. Rajzoljunk az $AC$ átfogó fölé félkört, majd $A$-ból, mint középpontból, $AB$ sugárral körívet. Messe ez a körív a félkört $D$-ben. Mekkora a $BCD$ síkidom területe?   3. Bizonyítsuk be, hogy az $5$ az egyetlen olyan pozitív prímszám, amelynek négyzete öt darab pozitív prímszám négyzetének összegeként állítható elő!   4. Mutassuk meg, hogy ha $a$, $b$, $c$ egy háromszög oldalainak hossza, akkor $\begin{array}{c}{\displaystyle 3\le \frac{{\left(a+b+c\right)}^2}{ab+bc+ca}<4.}\end{array}$     II. kategória: Nem speciális tantervű gimnáziumi tanulók       1. Van-e olyan valós $\left(x;y\right)$ számpár, amelyre teljesül, hogy $\begin{array}{c}{\displaystyle \frac{x^2\left(x+1\right)}{y+1}+\frac{y^2\left(y-1\right)}{x-1}=\frac{2}{y+1}-\frac{2}{x-1}?}\end{array}$   2. Az $ABC$ háromszög $AB$ oldalának Thálesz-köre az $AC$ oldalt a $P$, a $BC$ oldalt pedig a $Q$ pontban metszi. Mekkora az $ACB$ szög, ha a $PQ$ szakasz felezi az $ABC$ háromszög terrületét?   3. Öt pozitív prímszám négyzetének összege egy $p$ (pozitív) prímszám négyzete. Határozzuk meg $p^2$ értékét!   4. Mutassuk meg, hogy ha $a$, $b$, $c$ egy háromszög oldalainak hossza, akkor $\begin{array}{c}{\displaystyle 3\le \frac{{\left(a+b+c\right)}^2}{ab+bc+ca}<4.}\end{array}$   Harmadik (döntő) forduló       I. kategória: Szakközépiskolások       1. Hányféleképpen lehet megválasztani az $a$, $b$, $x$, $y$ pozitív egész számokat úgy, hogy teljesüljön a következő három feltétel: ‐ $x$ és $y$ legnagyobb közös osztója $a$; ‐ $x$ és $y$ legkisebb közös többszöröse $b$; ‐ $a$ és $b$ szorzata ${10}^{1997}$?   2. Az $AB$ átmérőjű egységsugarú $k_1$ kört az $e$ egyenes a $B$ pontban érinti. Egy $r$ sugarú $k_2$ kör kívülről érinti a $k_1$ kört az $A$-tól és $B$-től különböző pontban, továbbá érinti az $e$ egyenest is. Az $A$ pontból a $k_2$ körhoz húzott egyik érintő érintési pontja $C$. Bizonyítsuk be, hogy tetszőleges $r$ esetén az $ABC$ háromszög egyenlő szárú!   3. Igazoljuk, hogy ha egy egyenlő szárú háromszög szára $b$, beírt körének sugara pedig $r$, akkor $\frac{b}{r}>3$.         II. kategória: Nem speciális matematika tantervű gimnáziumi tanulók       1. Két párhuzamos egyenes közül az egyiken $n$ darab, a másikon $k$ darab pontot jelöltünk ki. Tekintsük az összes olyan háromszöget, amelyeknek csúcsai a kijelölt pontok közül valók. a) Igazoljuk, hogy $n$ és $k$ megválasztható úgy, hogy a háromszögek száma tetszőleges, adott négyzetszám legyen! b) Bizonyítsuk be, hogy a háromszögek száma nem lehet $3$-nál nagyobb prímszám!   2. Az $AB$ átmérőjű egységsugarú $k_1$ kört az $e$ egyenes a $B$ pontban érinti. Egy $r$ sugarú $k_2$ kör kívülről érinti a $k_1$ kört az $A$-tól és $B$-től különböző pontban, továbbá érinti az $e$ egyenest is. Az $A$ pontból a $k_2$ körhoz húzott érintő egyik érintési pontja a $C$ pont. Bizonyítsuk be, hogy az $AC$ szakasz hossza független az $r$ sugár hosszától!   3. Igazoljuk, hogy ha egy egyenlő szárú háromszög szára $b$, beírt körének sugara pedig $r$, akkor $\frac{b}{r}>3$.         III. kategória: Speciális matematika tantervű gimnáziumi tanulók       1. Hányféleképpen lehet megválasztani az $a$, $b$, $x$, $y$, $z$ pozitív egész számokat úgy, hogy teljesüljön a következő három feltétel: ‐ $x$, $y$ és $z$ legnagyobb közös osztója $a$; ‐ $x$, $y$ és $z$ legkisebb közös többszöröse $b$; ‐ $a$ és $b$ szorzata ${10}^{1997}$?   2. Igazoljuk, hogy ha egy derékszögű háromszög lefedhető két darab $1$ egység sugarú körlappal, akkor területe legfeljebb $\frac{3\sqrt[]{3}}{2}$ területegység!   3. Rendelkezésünkre áll tetszőleges számú $3$ egység, $5$ egység és $8$ egység oldalú négyzetlap. Ezekkel egy $1997$ egység oldalú négyzetlapot kell hézagmentesen és átfedés nélkül kirakni. Igazoljuk, hogy a kirakáshoz mindhárom fajta négyzetlapot fel kell használni! Adjunk is meg egy megfelelő kirakást!   Az 1996/97. évi Arany Dániel Matematikai Tanulóverseny eredményei   KEZDŐK       I. kategória: Szakközépiskolások     A bizottság I. díjat nem adott ki. II. díj:Nabadán János, Békéscsaba, Széchenyi I. Közg. és Külkeresk. Szki.,  tanára: Rókáné Rózsa Anikó. III. díj:Magyari Máté, Vác, Boronkay Gy. Műszaki Középiskola),  tanára: Mindáné Kolostori Nóra;  Tamás Katalin, Békéscsaba, Széchenyi I. Közgazd. és Külkeresk. Szki.,  tanára: Rókáné Rózsa Anikó. I. dicséret: Kiss Bálint, Vác, Boronkay Gy. Műszaki Középiskola, tanára: Mindáné Kolostori Nóra; Tót Edit (Makó, Erdei F. Keresk. és Közg. Szki., tanára: Szabó Istvánné. II. dicséret: Hegedüs Zoltán Csaba, Miskolc, Andrássy Gy. Műszaki Középiskola, tanára: Gonda Gáspár; Varga Erika, Budapest, Varga J. Közgazd. Szki., tanára: Vörös Sándor; Győr Gyula, Budapest, Neumann J. Számítástechn. Szki., tanára: Jakus Gabriella; Horváth Zsolt, Kaposvár, Naszlopy G. Közgazd. Szki., tanára: Farkas Éva; Kovács Annamária, Budapest, Varga J. Közgazd. Szki., tanára: Vörös Sándor; Kiss Andrea, Budapest, Varga J. Közgazd. Szki., tanára: Vörös Sándor; Györfi Gábor, Budapest, Hunfalvy J. Közgazd. Szki., tanára: Angyal Mária.     II. kategória: Nem speciális matematika tantervű gimnáziumi tanulók     I. díj: Zábrádi Gergely, Győr, Révai M. Gimnázium), tanára: Szíjártó Miklósné. II. díj: Antók Péter, Budapest, Radnóti M. Gyakorlóiskola,  tanára: Marcsek Gábor;  Baharev Ali, Budapest, ELTE Apáczai Cs. J. Gyak. Gimnázium,  tanára: Falta Zoltán;  Gyenes Zoltán, Budapest, ELTE Apáczai Cs. J. Gyak. Gimnázium,  tanára: Drozdy Győzőné;  Máthé András, Budapest, ELTE Apáczai Cs. J. Gyak. Gimnázium,  tanára: Tóth Attila. III. díj: Hadházi Ádám, Eger, Dobó István Gimnázium,  tanára: Homolyáné Nagy Irma;  Hegedűs Ákos, Pécs, Ciszterci Rend Nagy L. Gimnáziuma,  tanára: Tornyos Tivadarné;  Ivaskó György, Baja, III. Béla Gimnázium,  tanára: Királyné Nagy Éva;  Oláh István, Nyíregyháza, Krúdy Gy. Gimnázium,  tanára: Konczné Végh Leona. Dicséret: Antal István, Budapest, Veres Péter Gimnázium, tanára: Rácz Mihályné; Herczeg Géza, Szolnok, Varga Katalin Gimnázium, tanára: Dalmadiné Nagy Ilona; Horváth Krisztina, Bonyhád, Petőfi S. Evangélikus Gimnázium, tanára: Kovács Balázsné; Martin Tamás, Eger, Pásztorvölgyi Gimnázium, tanára: Hevesi Zoltán; Soltész Noémi, Budapest, ELTE Apáczai Cs. J. Gimnázium, tanára: Drozdy Győzőné.     III. kategória: Speciális matematika tantervű gimnáziumi tanulók     I. díj: Kajtár Márton, Fazekas M. Főv. Gyak. Gimnázium,  tanárai: Surányi László, Beleznay Ferenc, Pósa Lajos, Fazakas Tünde. II. díj: Ungi Tamás, Szeged, Radnóti M. Gimnázium,  tanárai: Schultz János, Vincze István. III. díj: Flach Attila, Szeged, JATE Ságvári E. Gimnázium,  tanárai: Vargáné Nádházi Ágnes, Némethné Varga Éva;  Hesz Zoltán, Fazekas M. Főv. Gyak. Gimnázium,  tanárai: Surányi László, Beleznay Ferenc, Fazakas Tünde; Nagy Máté, Budapest, Árpád Gimnázium,  tanárai: Gyimesi Róbert, Mikusi Imre;  Pozsonyi Gergő, Fazekas M. Főv. Gyak. Gimnázium,  tanárai: Surányi László, Beleznay Ferenc, Fazakas Tünde. I. dicséret: Bárány Zsófia, Fazekas M. Főv. Gyak. Gimnázium, tanárai: Beleznay Ferenc, Surányi László; Csiszár Gábor, Budapest, Szent István Gimnázium, tanára: Juhász István, Rácz János; Hudomiet Péter, Fazekas M. Főv. Gyak. Gimnázium, tanárai: Beleznay Ferenc, Surányi László. II. dicséret: Gajári Dávid, Fazekas M. Főv. Gyak. Gimnázium, tanárai: Surányi László, Beleznay Ferenc, Fazakas Tünde; Lábó Eszter, Fazekas M. Főv. Gyak. Gimnázium, tanárai: Beleznay Ferenc, Surányi László; Lábó Melinda, Fazekas M. Főv. Gyak. Gimnázium, tanárai: Beleznay Ferenc, Surányi László; Nagy Gábor, Miskolc, Földes F. Gimnázium, tanárai: Vass István, Veres Pál.     HALADÓK         I. kategória: Szakközépiskolások     I. díj: Gera Zoltán, Budapest, Neumann J. Számítástechnikai Szki.,  tanára: Mészáros Tünde. II. díj: Mihajlik Gábor, Vác, Boronkay Gy. Műszaki Középiskola,  tanára: Fábián Gábor;  Szeremi Katalin, Eger, Egri Közgazdasági Szki.,  tanára: Nagy Lajosné. III. díj: Horváth Zsolt, Székesfehérvár, Hunyadi M. Közg. Szki.,  tanára: Székely Ferencné. Dicséret: Barák Tamás, Békéscsaba, Széchenyi I. Közg. és Külker. Szki., tanára: Schédl Ilona; Sípos Péter, Budapest, Trefort Á. Kéttannyelvű Szki. és Gimn., tanára: Dunajszki Zsuzsanna; Varga Gábor, Paks, Energetikai Szakképzési Intézet, tanára: Árkoszállási Tibor.     II. kategória: Nem speciális matematika tantervű gimnáziumi tanulók     I díj: Bosznai Tamás, Budapest, ELTE Apáczai Cs. J. Gyak. Gimn.,  tanára: Pósfai Péter;  Erős Zsolt, Békéscsaba, Belvárosi Ált. Isk. és Gimn.,  tanára: Kelemenné Kis Ilona;  Gueth Krisztián, Szombathely, Kanizsai Dorottya Gimn.,  tanára: Sándor Endre;  Pál András, Budapest, Eötvös J. Gimn.,  tanárai: Gyengéné Beé Andrea, Somfai Zsuzsa. II. díj: Lengyel Tímea, Budapest, Munkácsy M. Gimn.,  tanára: Gajdos Katalin. III. díj: Pandúr Sándor, Budapest, ELTE Apáczai Cs. J. Gyak. Gimn.,  tanára: Pósfai Péter;  Szakács László, Budapest, Jedlik Á. Gimn.,  tanára: Gudenus Lászlóné, Sebestyén Zoltán. I. dicséret: Bujdosó Attila, Budapest, Veres Péter Gimn., tanára: Varga Mária; Mecz Balázs, Pápa, Türr István Gimn., tanárai: Bátyi Gyuláné, Spissich László; Boros Márton, Budapest, Eötvös J. Gimn., tanárai: Somfai Zsuzsa, Gyengéné Beé Andrea; Pszota Anikó, Vác, Madách I. Gimn., tanára: Ujhelyi László. II. dicséret: Sztranyák Zsolt, Kecskemét, Katona J. Gimn., tanára: Szablics Bálint; Spisák Ferenc, Eger, Neumann J. Közg. Szki. és Gimn., tanára: Szakaliné Haraszti Éva; Rácz Balázs, Budapest, Veres Péter Gimn., tanára: Varga Mária; Varga Csilla, Budapest, Eötvös J. Gimn., tanára: Somfai Zsuzs, Gyengéné Beé Andrea; Gönci Balázs, Budapest, Móricz Zs. Gimn., tanárai: Lux Judit, Pósa Lajos; Kiss Gergely, Kecskemét, Katona J. Gimn., tanára: Reiter István; Lovas Róbert, Csongrád, Batsányi J. Gimn., tanára: Papp Ferencné.     III. kategória: Speciális matematika tantervű gimnáziumi tanulók     I. díj: Terpai Tamás, Fazekas M. Főv. Gyak. Gimn.,  tanárai: Táborné Vincze Márta, Beleznay Ferenc, Pósa Lajos. II. díj: Horváth Gábor, Debrecen, Fazekas M. Gimn.,  tanára: Nagy Erzsébet,  Végh László, Debrecen, Fazekas M. Gimn.,  tanára: Nagy Erzsébet. III. díj: Förhécz András, Székesfehérvár, Teleki Blanka Gimn.,  tanárai: Sipos Imre, Mihályi Gyula;  Patakfalvi Zsolt, Fazekas M. Főv. Gyak. Gimn.,  tanárai: Táborné Vincze Márta, Beleznay Ferenc;  Lukács László, Miskolc, Földes F. Gimn.,  tanárai: Gulyás Tibor, ifj. Szabó Kálmán. I. dicséret: Hesz Gábor, Fazekas M. Főv. Gyak. Gimn., tanárai: Táborné Vincze Márta, Beleznay Ferenc; Juhász András, Fazekas M. Főv. Gyak. Gimn., tanárai: Táborné Vincze Márta, Beleznay Ferenc. II. dicséret: Farkas Claudia, Budapest, Szent István Gimn., tanárai: Magyar Zsolt, Lászlóné S. Stefánia; Györey Bernadett, Székesfehérvár, Teleki Blanka Gimn., tanárai: Sipos Imre, Mihályi Gyula; Lenk Sándor, Zalaegerszeg, Zrínyi M. Gimn., tanárai: Pálovics Róbert, Németh László; Pap Júlia, Debrecen, Fazekas M. Gimn., tanára: Nagy Erzsébet; Szabó Péter, Fazekas M. Főv. Gyak. Gimn., tanárai: Táborné Vincze Márta, Beleznay Ferenc, Koblinger Egmont, Nagy Dániel, Recski András, Pátzay György; Szabó Zsolt, Fazekas M. Főv. Gyak. Gimn., tanárai: Táborné Vincze Márta, Beleznay Ferenc; Szécsi Vajk, Fazekas M. Főv. Gyak. Gimn., tanárai: Táborné Vincze Márta, Beleznay Ferenc.