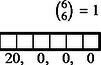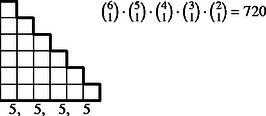Kezdőlap


Cím:	RISK - egy társasjáték kockázata
Szerző(k):	Blázsik Zoltán
Füzet:	1997/május, 257 - 261. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Játékaink sokszor tálcán kínálják az igazi matematikai problémákat. Ha matematikus szemmel tekintünk stratégiai játékainkra, akkor lépten-nyomon felvetődik bennünk egy-egy kérdés, amelyre ha tudnánk válaszolni, jobban (vagy esetleg tökéletesen) játszhatnánk kedvenc játékunkat. Szerencsére a legjobb játékaink olyan bonyolultak, hogy nem vagyunk képesek matematikai elemzéssel kimutatni az egyik vagy másik fél győzelmét, döntetlenét (még akkor sem, ha tudjuk, hogy létezik nyerő stratégia).
Ebben a cikkben a ,,RISK'' (kockázat, kockáztat) nevű érdekes, komplex társasjáték egy részproblémáját oldjuk meg. A játék a Föld országainak birtoklásáért folyik, többen játszhatják. A játékosok egymás előtt titkolt célok eléréséért küzdenek, bizonyos számú katonát állomásoztatva bizonyos országokban. Egy országban csak egy játékos katonái lehetnek, az ott lévő katonák tulajdonosa birtokolja az országot. Az elérendő célok általában a területszerzéssel függenek össze. (pl.: Foglald el Európát és Ázsiát!)
Egy játékos megtámadhat és esetleg elfoglalhat egy országot. Hogy mikor és hogyan? Ezt a szabályt precízebben fogalmazzuk meg, hiszen ez vizsgálatunk tárgya.
Ha a világ térképén az $A$ és $B$ országok szomszédosak, és az $A$ országban a soron következő játékos katonái állomásoznak, akkor az $A$ -beli katonák irányítója (a támadó) megtámadhatja a $B$ országot, amelyben a védő katonái őrködnek.
A megtámadáskor egyetlen puskalövés sem hallatszik, helyette a támadó feldob 3 piros dobókockát (a szokásos 6 oldalút, rajta az 1, 2, 3, 4, 5, 6 számokkal), míg a védő 3 kék dobókockával dob. Ezután a támadó a piros kockákat nagyság szerint csökkenő sorrendbe rakja, ugyanezt teszi a védő a kékekkel. (Természetesen lehetnek megegyező számok.) Ezután a három-három dobókocka számait páronként összehasonlítják, a legnagyobbat a legnagyobbal, a középsőt a középsővel, a legkisebbet a legkisebbel. Ahol a piros dobókockával dobott szám nagyobb, mint a kék párján levő, ott a támadó nyer, ahol kisebb vagy egyenlő, ott a védő. A dobás után a védő annyi katonát vesz le a $B$ országból, ahány helyen a támadó nyert, míg a támadó annyi katonával csökkenti az $A$ országban állomásozó kontingensét, ahány helyen a védő nyert. A támadás egymás után többször ismételhető. A támadó akkor foglalhatja el a $B$ országot, ha elfogynak a védő katonái $B$ -ből, míg neki marad legalább két katonája $A$ -ban. (Ekkor serege egy részével bevonulhat $B$ -be.)
Vajon mikor érdemes támadni? Nyilván, ha a támadó túlerőben van. Ekkor remélheti, hogy serege tovább kitart, mint a védőé.
A védőnek komoly előnye van, egy pozícióban az egyenlő neki kedvez! A játék nem szimmetrikus. Vajon mekkora valószínűséggel nyer a védő $3 : 0$ -ra? Mekkora az esélye annak, hogy $1 : 2$ -re veszít? Várhatóan átlagosan hány katonát veszít a támadó egy akcióban? Ezekre a kérdésekre keressük a választ.
A dobókockák összehasonlítás előtti rendezése alaposan megkülönbözteti a problémát a szokásos kombinatorikai feladatoktól. Érdemes itt egy kicsit elgondolkodni!
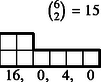
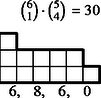
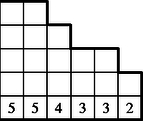
Nézzünk egy példát: a támadó dobásai: 5, 4, 2; a védő dobásai: 5, 3, 3. A védő $2 : 1$ -re nyer. A hat dobott értéket rendezzük fogyó sorozatba: 5, 5, 4, 3, 3, 2. Egy lépcsővel ábrázolhatjuk a számhatost (1. ábra), ahol a lépcső magassága a dobott érték.
Fordítsuk meg, tegyük fel, hogy adott egy lépcső (a hat dobott érték csökkenő sorrendben rendezve), akkor az akció értékelése attól függ, melyik 3 érték jött ki pirossal, melyik 3 kékkel. Nyilván egy adott lépcső $(\binom{6}{3}) = 20$ -féleképpen színezhető ki 3 piros‐3 kékre. Bármely lépcső esetén megszámlálhatjuk, hogy a 20 esetből hányszor nyer a védő $3 : 0$ -ra, $2 : 1$ -re, illetve veszít $1 : 2$ -re, $0 : 3$ -ra.

Ez a lépcsőnkénti értékelés nehezen lenne formalizálható. Viszont két lépcső csak akkor különbözik egymástól lényegesen a kiértékelés szempontjából, ha
a) a 6 dobott érték közül az egyenlők száma eltérő
b) ha a dobott 6 számot sorbarendezve és közéjük a megfelelő relációjeleket beírva (pl.

5 = 5 > 4 > 3 = 3 > 2

) az öt relációjel valamelyik helyen eltér. (A győzelem vagy veszteség kiértékelése szempontjából tehát megegyezik az 5 5 4 3 3 2 és pl. a 6 6 3 2 2 1: mindkettőben négyféle érték és azonos relációk fordulnak elő.)
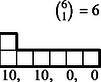
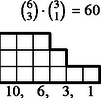
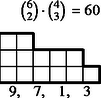
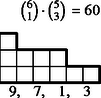
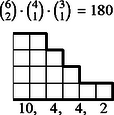
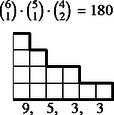
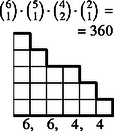
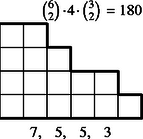
Nem lényeges tehát az, milyen magasak a lépcsőfokok, de hogy milyen hosszúak, az igen. A példánkban szereplő kimenetel típusát (

=

>

>

=

>

) 1 magasságú lépcsőfokokkal ábrázolhatjuk (2. ábra). A lépcső magassága ezentúl azt jelenti, hányféle érték fordulhat elő a dobások között. A lépcső alá írtuk az értékelést, a védő szempontjából csökkenő sorrendbe: a négy szám rendre azt jelenti, hogy a lehetséges 20 esetből hányszor nyer a védő

3 : 0

-ra, hányszor

2 : 1

-re, hányszor veszít

1 : 2

-re és

0 : 3

-ra. A lépcső fölé írtuk a lépcső ,,súlyát'', vagyis azt, hogy ha a dobások között pontosan négy érték fordul elő, akkor hány esetben adódik közülük a rendezés után éppen ez a lépcső. A hat kockából valamelyik kettő lesz a két legnagyobb (

(\binom{6}{2})

eset), négyből egy a harmadik (

(\binom{4}{1})

), háromból kettő a negyedik és ötödik (

(\binom{3}{2})

), tehát

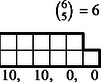
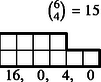
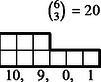
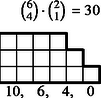
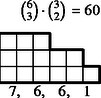
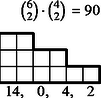
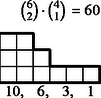
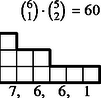
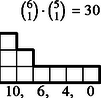
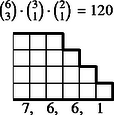
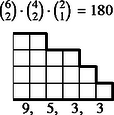
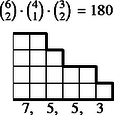
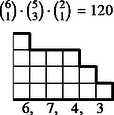
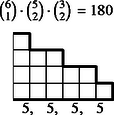
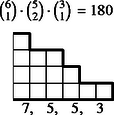
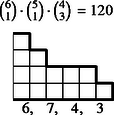
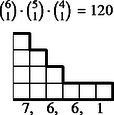
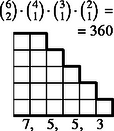
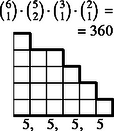
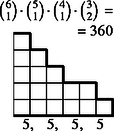
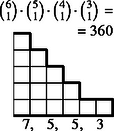
(\binom{6}{2}) \cdot (\binom{4}{1}) \cdot (\binom{3}{2}) = 180

esetben.
6 esetet különböztetünk meg a dobott értékek száma szerint, s egy-egy esetben a következő lépcsőtípusokat (3. ábra):
Az összes dobások között egyetlen érték 6-féleképpen fordulhat elő, két érték

(\binom{6}{2})

-féleképpen, három

(\binom{6}{3})

, négy

(\binom{6}{4})

, öt

(\binom{6}{5})

, végül hat különböző érték csak

(\binom{6}{6}) = 1

-féleképpen.
Összesen

6^{6}

kockadobás lehet. Attól függően, hogy melyik kocka piros, melyik kék, lesz négy eset; jelöljük rendre

p_{1}

p_{2}

p_{3}

p_{4}

-gyel annak a valószínűségét, hogy egy támadó akció esetén a védő szempontjából

3 : 0

2 : 1

1 : 2

0 : 3

lesz az eredmény.
A 3. ábra alapján számolva:

\begin{matrix} \begin{matrix} p_{1} = \frac{1}{6^{6}} [6 \cdot 20 + (\binom{6}{2}) \cdot (10 \cdot 6 + 16 \cdot 15 + 10 \cdot 20 + 16 \cdot 15 + 10 \cdot 6) + \\ + (\binom{6}{3}) \cdot (10 \cdot 30 + 7 \cdot 60 + 10 \cdot 60 + 9 \cdot 60 + 14 \cdot 90 + 10 \cdot 60 + 6 \cdot 30 + 9 \cdot 60 + 7 \cdot 60 + 10 \cdot 30) + \\ + (\binom{6}{4}) \cdot (7 \cdot 120 + 9 \cdot 180 + 7 \cdot 180 + 10 \cdot 180 + 6 \cdot 120 + 5 \cdot 180 + 7 \cdot 180 + 6 \cdot 120 + 9 \cdot 180 + 7 \cdot 120) + \\ + (\binom{6}{5}) \cdot (7 + 5 + 6 + 5 + 7) \cdot 360 + 5 \cdot 720] \cdot \frac{1}{20} = \frac{17 871}{6^{6}} \approx 0,3830. \end{matrix} \end{matrix}

Egy érték:

Két érték:

Három érték:

Négy érték:

Öt érték:

Hat érték:

\begin{matrix} \begin{matrix} p_{2} = \frac{1}{6^{6}} [(\binom{6}{2}) \cdot (10 \cdot 6 + 0 \cdot 15 + 9 \cdot 20 + 0 \cdot 15 + 10 \cdot 6) + \\ + (\binom{6}{3}) \cdot (6 \cdot 30 + 6 \cdot 60 + 6 \cdot 60 + 7 \cdot 60 + 0 \cdot 90 + 6 \cdot 60 + 8 \cdot 30 + 7 \cdot 60 + 6 \cdot 60 + 6 \cdot 30) + \\ + (\binom{6}{4}) \cdot (6 \cdot 120 + 5 \cdot 180 + 5 \cdot 180 + 4 \cdot 180 + 7 \cdot 120 + 5 \cdot 180 + 5 \cdot 180 + 7 \cdot 120 + 5 \cdot 180 + 6 \cdot 120) + \\ + (\binom{6}{5}) (5 + 5 + 6 + 5 + 5) \cdot 360 + 5 \cdot 720] \cdot \frac{1}{20} = \frac{12 348}{6^{6}} \approx 0,2647 \end{matrix} \end{matrix}

\begin{matrix} \begin{matrix} p_{3} = \frac{1}{6^{6}} [(\binom{6}{2}) \cdot (4 \cdot 15 + 4 \cdot 15) + \\ + (\binom{6}{3}) \cdot (4 \cdot 30 + 6 \cdot 60 + 3 \cdot 60 + 1 \cdot 60 + 4 \cdot 90 + 3 \cdot 60 + 6 \cdot 30 + 1 \cdot 60 + 6 \cdot 60 + 4 \cdot 30) + \\ + (\binom{6}{4}) \cdot (6 \cdot 120 + 3 \cdot 180 + 5 \cdot 180 + 4 \cdot 180 + 4 \cdot 120 + 5 \cdot 180 + 5 \cdot 180 + 4 \cdot 120 + 3 \cdot 180 + 6 \cdot 120) + \\ + (\binom{6}{5}) \cdot (5 + 5 + 4 + 5 + 5) \cdot 360 + 5 \cdot 720] \cdot \frac{1}{20} = \frac{10 017}{6^{6}} \approx 0,2147 \end{matrix} \end{matrix}

p_{4} = 1 - (p_{1} + p_{2} + p_{3}) = \frac{46656 - (17871 + 12348 + 10017)}{46656} = \frac{6420}{6^{6}} \approx 0,1376

.
Láthatjuk, hogy mennyit jelent a védő előnye döntetlen esetén! Például a

3 : 0

-s győzelemre a védőnek majdnem háromszor akkora az esélye, mint a támadónak! Gondoltuk volna?
A várható katonai veszteség a támadónál:

\begin{matrix} 3 \cdot \frac{17 871}{6^{6}} + 2 \cdot \frac{12 348}{6^{6}} + 1 \cdot \frac{10 017}{6^{6}} = \frac{88 326}{6^{6}} \approx 1,8931. \end{matrix}

A várható katonai veszteség a védőnél:

\begin{matrix} 1 \cdot \frac{12 348}{6^{6}} + 2 \cdot \frac{10 017}{6^{6}} + 3 \cdot \frac{6420}{6^{6}} = \frac{51 642}{6^{6}} \approx 1,1069. \end{matrix}

Ez az az érték, amit tudnia kell a támadónak. Ha túlereje nem éri el ezt az arányt, akkor kisebb az esélye a területszerzésre. Természetesen indíthat támadást bízva jó szerencséjében. (Ezért ,,rizikó'', ,,kockázat'' a játék neve.) Ha a kezdeti akciók jól sikerülnek, folytathatja növekedő eséllyel, míg a ,,megalapozott'' inváziót is érdemes leállítani, ha kezdeti kudarcok érik.
A játék több mint a matematikája! Már majdnem az élet.

Blázsik Zoltán, Szeged