| Cím: | Néhány egészen általános konstrukció | ||
| Szerző(k): | Fried Ervin | ||
| Füzet: | 1997/április, 193 - 206. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Szakmai cikkek | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A századunk elejére‐közepére kialakult matematika egyik alapvető jellemzője az ,,absztrakt struktúrák'' vizsgálata. Feladatunk a következő lesz: Képzeljük el, hogy minden egyes halmaz egy ,,mikrovilág'', amelynek a belsejébe nem láthatunk be. Itt a külvilágban csak annyit látunk, hogy minden egyes halmaz egy objektum, de látjuk azokat a függvényeket ‐ például nyilak formájában ‐, amelyek egyik halmazt a másikba képezik. Ezenkívül még az igazán különböző függvényeket meg is tudjuk különböztetni egymástól. (Később még néhány dolgot fel kell tennünk e nyilak kapcsolatáról.) A direkt szorzat elemei az alakú párok, ahol és . Ez azonnal indukál természetes módon két függvényt, az és vetítéseket úgy, hogy és . Ezek a függvények annyira szervesen hozzátartoznak a direkt szorzathoz, hogy célszerűbb rögtön hozzávenni az elnevezéshez. Tekintettel arra, hogy a most megadandó definícióban nem lesz benne, hogy az pontosan a megfelelő párokból áll, ezért az elnevezést is egy kissé megváltoztatjuk; elhagyjuk a ,,direkt'' jelzőt: Az és halmazok szorzata egy pár Ilyen tulajdonságú pár persze rengeteg van. Tetszőleges halmaz esetén létezik az pár. Éppen ezért meg kell találnunk a direkt szorzat legjellemzőbb, függvényekkel megfogalmazható tulajdonságait. A legszembetűnőbb talán az, hogy -ban is és -ben is minden elem fellép képként. Sajnos ezt a tulajdonságot csak akkor tudjuk direkt módon megfogni, ha ,,bekukucskálunk'' a halmazokba. Valami indirekt lehetőséget az ad, hogy tulajdonképpen tudjuk, hogy ilyen függvények vannak. Ha tehát olyan kitétellel fogalmazunk, hogy ,,minden függvényre'', akkor ezek között azok a függvények is ott lesznek, amelyek -ra, illetve -re képeznek. Tekintsünk tehát most egy tetszőleges halmazt, amelyet valamilyen módon leképezünk -ba is és -be is: úgy, hogy valahányszor adott az pár, Mit tudunk erről az esetről mondani? Például azt, hogy az halmaz tetszőleges elemére és . Eszerint a halmazban ott van a pár. Ekkor viszont megadható az függvény. Ezt most írjuk le gyorsan: mindig létezik egy függvény úgy, hogy Az, hogy milyen tulajdonságú ez a függvény, már látszik, hiszen és . Csak az a kérdés, hogy mit értsünk azon, hogy ,,egy függvényt a másik után alkalmazunk''? Az eredmény ismét egy függvény lesz, amit tehát tekinthetünk egy ,,függvényeken értelmezett műveletnek''. Vigyázni kell azonban arra, hogy ez a művelet nem mindig végezhető el. Ha és függvények, akkor jelölje azt a függvényt, amelyet definiál, tetszőleges esetén. Könnyen látható, hogy ez a szorzás asszociatív. Ezzel a szorzással megfogalmazva: és , Ezzel már sikerült kifejezni azt, hogy az elképzelt direkt szorzat elég nagy, pontosabban szólva benne van minden alakú elem. Példának okáért, ha egy pár teljesíti a megkívánt feltételt, akkor -nek a direkt szorzatot, -nek és -nek a megfelelő vetítést választva a következőket kapjuk: és következtében és . Másszóval, ha az és párt ugyanabba a elembe viszi, akkor Tegyük fel, hogy az alakú elemeken kívül tartalmaz még egy további elemet. Ekkor és ; és így persze is eleme -nek. Nyilván , de ezt a két elemet ,,nem tudjuk megkülönböztetni''. Pontosan ez ad lehetőséget ennek az újabb elemnek a kizárására. Az eredeti függvény mellett ugyanis létezik egy olyan függvény is, amelyik azokat az elemeket, amelyeket a -re képezett a -re képezi, de a többi elem képe változatlan marad. Így . Ezzel szemben és . A ,,felesleges'' elem tehát kizárható azzal, hogy: és ez a függvény egyértelműen meghatározott. Összefoglalva: Az és halmazok direkt szorzata egy pár úgy, hogy valahányszor adott az pár, mindig létezik egy függvény úgy, hogy és , és ez a függvény egyértelműen meghatározott. Az eddigiekből az már világos, hogy a direkt szorzat (beleértve az adott halmazokra való függvényeket is!) rendelkezik az itt megfogalmazott tulajdonsággal. Az viszont egyáltalában nem látszik, hogy más halmaz és hozzátartozó függvénypár nem lehet ugyancsak ilyen tulajdonságú. Persze, ha ,,belekukucskálunk'' a halmazokba, akkor láthatjuk, hogy más eset nem létezhet. Pontosabban szólva más eset nem létezhet. Ha ugyanis minden elemet ,,átnevezünk'', például helyett egy -vel jelölt új elemet írunk, akkor ezeknek az elemeknek a halmaza is éppen olyan megfelelő lesz; még az adott halmazokra való függvények is megadhatók úgy, hogy és . Ez az átnevezés egy kölcsönösen egyértelmű megfeleltetést jelent. Ez a fogalom így persze ugyancsak egy ,,belül'' megfogalmazott tulajdonság. ,,Kívül'' csak annyit látunk, hogy az a és függvény, amelyet , illetve definiál, egymásnak inverzei; vagyis mind az , mind a a megfelelő halmazok identikus leképezései, azaz minden elemet önmagára képeznek. Ezzel a ,,szorzat-tulajdonsággal'' csak a kölcsönösen egyértelmű függvények rendelkezhetnek: Legyenek és olyanok, hogy mind a mind az az identitás. Ekkor tetszőleges -beli -ra és -beli -re és . Eszerint minden elem fellép -nál képként, de ha , akkor . Hasonlóképpen látható be, hogy is kölcsönösen egyértelmű; és akkor már természetesen egymás inverzei. Ezzel ismét egy újabb akadályba ütköztünk. A kölcsönösen egyértelmű függvények ,,értelmezésétől'' megszabadultunk, de csak azon az áron, hogy az identikus leképezéseket kellene leírni. Tulajdonképpen ez nem nehéz, hiszen: pontosan akkor identitás (= identikus függvény), ha bármely és esetén és . Visszatérve a kölcsönösen egyértelmű függvényre: akkor és csak akkor kölcsönösen egyértelmű, ha van olyan , amelyre és . Most már csak azt kell kimondani, hogy: Minden -hoz tartozik egy identitás. Azt már bárki könnyen bebizonyíthatja, hogy az identitások egyértelműen meghatározottak. A továbbiakban a jobb áttekinthetőség kedvéért úgynevezett diagramokat fogunk használni. Ez azt jelenti, hogy a halmazokat, mint ,,pontokat'' fogjuk ábrázolni, a függvényeket pedig mint nyilakat, amelyekre (vagy mellé) odaírjuk a szóbanforgó függvény nevét. Maga a direkt szorzat is felírható diagrammal: 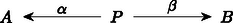 Ha odaírjuk a definíciót ,,hordozó'' többi függvényt is, akkor a következő diagramhoz jutunk: 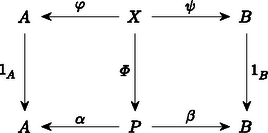 Ez a diagram még azzal a tulajdonsággal is rendelkezik, hogy és . Ez könnyen leolvasható a diagramról. Általában: Ha egy diagram bármely pontjából a nyilak mentén egy másik ponthoz érve az érintett ,,függvények'' szorzatának eredménye nem függ az út megválasztásától, csupán annak kezdő- és végpontjától, akkor kommutatív diagramról beszélünk. A diagramok segítségével sokkal ,,látványosabban'' megfogalmazható az, hogy mit jelent a direkt szorzat egyértelműsége. Legyen 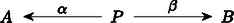 és és 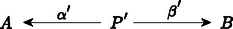 két, a direkt szorzatot definiáló diagram. Akkor létezik olyan és függvény, amelyek egymás inverzei és a 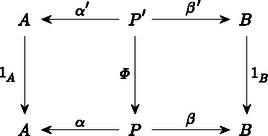 , valamint , valamint 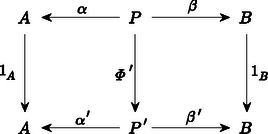 diagramok kommutatívak. Ez valami olyasmit jelent, hogy és nemcsak a halmazokon kölcsönösen egyértelműek, hanem a direkt szorzathoz tartozó két függvénypárt is ,,egymásba viszik''. Annak a belátására, hogy a fenti és valóban egymás inverzei, induljunk ki a most felírt két diagramból, amelyeknek a létezése abból következik, hogy 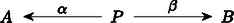 és és 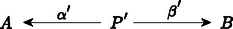 mindketten a direkt szorzatot jelentik. A fenti két diagramból a következő két diagramot kaphatjuk: 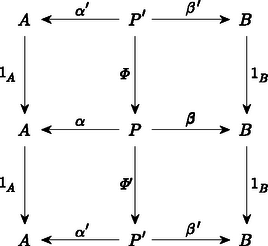 , valamint , valamint  Mindkét diagram esetében a ,,felső téglalap'' is és az ,,alsó téglalap'' is kommutatív diagram. Ebből egyszerű számolással azonnal következik, hogy az egész diagram is kommutatív, mindkét esetben. Kommutatív diagramokat kapunk tehát akkor is, ha a ,,középső sort'' elhagyjuk, és a függőleges nyilakhoz a megfelelő szorzatokat írjuk. Tekintettel arra, hogy az identitást önmagával szorozva ismét az identitást nyerjük, ezért 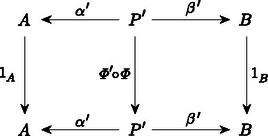 és és 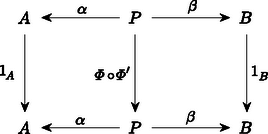 lesz az adódó két diagram. Teljesen hasonló diagramokat írhatunk fel úgy is, hogy a ,,középső'' függőleges nyíl mellé az identitást írjuk: 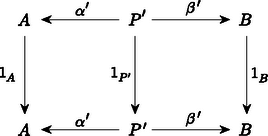 és és 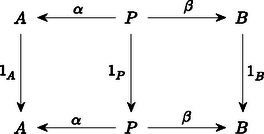 Ez a két diagram ugyancsak kommutatív. Tekintettel arra, hogy a direkt szorzat diagramban a középső nyilak egyértelműek és is is a direkt szorzat, ezért és ; ami valóban azt bizonyítja, hogy ez a két függvény egymásnak a fenti értelemben is inverze. Most pedig a diszjunkt unióra kellene térnünk, de ezt nem tesszük. Legalább is nem úgy, mint a direkt szorzatnál. Azért választottuk éppen a diszjunkt uniót a direkt szorzat párjának, mert ezek ,,duálisan viselkednek''. Ezen azt értjük, hogy a diszjunkt uniót ugyanúgy lehet definiálni, mint a direkt szorzatot, csak a nyilak irányát kell megváltoztatni. Eszerint: Az és halmazok diszjunkt uniója egy pár úgy, hogy valahányszor adott az pár, mindig létezik egy függvény úgy, hogy és , és ez a függvény egyértelműen meghatározott. A diszjunkt unió valóban rendelkezik ezzel a tulajdonsággal. Legyen és úgy definiálva, hogy elemei pontosan az és alakú elemek, ahol és . Tegyük fel most, hogy adottak a és függvények. Definiáljuk ezekután a -t úgy, hogy és . Biztos, hogy valóban a diszjunkt unióról van szó, mert ha -t a diszjunkt uniónak választjuk és -t, -t a megfelelő leképezéseknek, akkor soha nem lehet, így is lehetetlen. Most azt kellene belátni, hogy a fenti tulajdonsággal csak a diszjunkt unió rendelkezik. Erre viszont nincs szükség! Az a formális bizonyítás ugyanis, amit a direkt szorzatra adtunk, szóról szóra átvihető erre az esetre is, mert ott nem volt lényeges a függvények ,,iránya''; illetve csak abban történik változás, hogy a szorzást fordított sorrendben kell végezni. A továbbiakban ezeket a konstrukciókat absztraktul, teljes általánosságban fogjuk vizsgálni; majd megnézzük jelentésüket konkrét esetekben. A cikk első részében két halmazelméleti konstrukciót tárgyaltunk, a direkt szorzatot és a diszjunkt uniót. Mindkét esetben olyan leírást adtunk, amelyik ,,nem tekintett a halmazok belsejébe''; vagyis csak a halmazok közötti függvények egymáshoz való kapcsolatát használta. Emellett még az is teljesült, hogy e két fogalom leírása ,,duális'' volt, azaz a függvényeket leíró nyilak irányát kellett csupán megváltoztatni. Az első részben nem csak számos halmazelméleti konstrukciót soroltunk fel; de felsoroltunk olyan matematikai ágakat is, amelyek bizonyos értelemben hasonló jellegűek, mint a halmazelmélet. Ilyenek például a gráfok, vagy a csoportok, vagy a kommutatív csoportok, vagy a gyűrűk vagy a topologikus terek stb. Ezek esetében is lehetne definiálni a direkt szorzat és a diszjunkt unió fogalmát ‐ pontosabban szólva az ezeknek megfelelő fogalmakat. Ekkor a halmazok szerepét a megfelelő objektumok veszik át; a függvények helyére pedig csak olyan függvényeket vehetünk, amelyek ,,megtartják'' a szóbanforgó struktúrát. Gráfok esetében tehát csak azok a függvények jöhetnek szóba, amelyek ,,élt élbe visznek'', csoportok vagy gyűrűk esetében pedig csak azok, amelyek ,,megtartják'' a megfelelő műveleteket. Ezáltal sok eddigi függvény ,,kiesik''; ha például egy kölcsönösen egyértelmű függvény ,,nem tartja meg a struktúrát'', akkor egyáltalában szóba se jöhet egy diagramnál. Két fontos dolog azonban mindig megmarad. Az egyik az, hogy két ,,struktúratartó'' függvény szorzata is ilyen; a másik meg az, hogy az identitás minden struktúrát megtart. A kapott rendszer tehát kétféle ,,valamikből'' áll. Az egyik a objektumai, a másik azok a ,,valamik'', amelyek a függvények szerepét játsszák. Mivel ezekről nem is akarjuk feltenni, hogy függvények, ezért morfizmusnak fogjuk nevezni őket. Az ilyen rendszereket (a fent megfogalmazott kívánalmakkal együtt) kategóriáknak nevezik: Egy kategória két részből áll: az objektumokból és a morfizmusokból. Minden , párhoz hozzá van rendelve morfizmusok egy halmaza, és minden eleme pontosan egy halmazhoz tartozik. Azt, hogy úgy is kifejezzük, hogy , vagy , vagy , vagy . Nem követeljük meg, hogy -nek legyen eleme. (Például ha az gráfnak két szögpontja van, amelyek egy éllel vannak összekötve és a gráfban nincs él, akkor nem létezik olyan éltartó leképezés, amelyik -t -be vinné.) Egy kategóriában a következő axiómák teljesülését kívánjuk meg: 1.) Ha és , akkor létezik -ben egy általuk egyértelműen meghatározott elem. Ezt az elemet a továbbiakban a két adott elem szorzatának nevezzük és a ,,'' elhagyásával úgy jelöljük, hogy . 2.) Ha létezik az és szorzat, akkor léteznek az és szorzatok is; és megegyeznek. A fentiek ‐ mint látjuk ‐ a függvénykompozíció alapvető tulajdonságait rögzítik. Most még az identitás létét is ki kell kötni: 3.) Minden esetén létezik olyan , amelyre bármely és bármely esetén és . (A kategóriák bevezetésekor semmiféle konkrét alkalmazhatóságuk nem látszott. A fogalmak teljesen absztraktak és az első eredmények, amelyeket kategóriák segítségével értek el alig tűntek másnak, mint ismert eredmények bizonyításának. Ennek következtében nevezték el a kategóriákat absztrakt nonszensznek2.) Na mármost, tetszőleges kategóriában teljesen általánosan definiálhatjuk a szorzatot a már látott módon. Sőt ugyanúgy, mint a halmazok esetében is akármennyi (véges vagy végtelen sok) objektum szorzatáról is beszélhetünk. diagramok mindegyike kommutatív ( jelöli identitását). Mi csak olyan eseteket fogunk nézni, amikor az indexhalmaz véges, vagy a természetes számok halmaza. Az halmazt -nel, a természetes számok halmazát -nel fogjuk jelölni (tehát például ). Ha (a halmazok kategóriája), akkor ‐ mint láttuk ‐ () esetén elemei párok, és , illetve . Hasonlóképpen adódik a () szorzatra, hogy a ,,szorzat-objektum'' elemei olyan -elemű sorozatok, amelyekben az -edik elem az -edik objektumból való és az -edik morfizmus a sorozatot éppen erre az -edik komponensre képezi le, vagyis a direkt szorzat. Nem okoz gondot az () értelmezése sem; itt végtelen sorozatok lépnek fel. A következő, amit megnézünk, a gráfok kategóriája lesz. Mindenekelőtt meg kell mondani, mik objektumai és mik a morfizmusok. Nos, az objektumok az irányítatlan gráfok3. A morfizmusok definícója az szokott lenni, hogy olyan ,,valami'', ami a tartóhalmazokon egy függvény; s ha az gráf éle, akkor éle a gráfnak. Szinte triviális, hogy valóban egy kategóriát kaptunk. Nem nehéz belátni, hogy a gráfok kategóriájában a szorzatot a következőképpen kaphatjuk meg: Legyenek adva az gráfok (). Készítsük el a tartóhalmazok direkt szorzatát. Ennek egy és egy elemét akkor kössük össze éllel, ha az adott gráfok mindegyikében ott van a megfelelő él. A direkt szorzathoz tartozó morfizmust pedig adja meg. Érdemes felfigyelni a következőre: A gráfok kategóriájában az objektumok természetesen a gráfok. Az viszont már egyáltalában nem világos, hogy mik legyenek a morfizmusok. Miért ne lehetne a morfizmusok természetesnek vett ,,éltartás''-a mellett azt is megkívánni, hogy a ,,nem-él'' tulajdonságot is megtartsa. Ez azt jelenti, hogy ha nem az gráf éle, akkor sem éle a gráfnak. A kategória definíciójában szereplő axiómák most is triviálisan teljesülnek. Az történt csupán, hogy az előbbi kategória morfizmusai közül jó néhányat elhagytunk. Ennek az a furcsa következménye, hogy ebben a kategóriában nem mindig létezik szorzat. Tekintsük például a kételemű halmazon értelmezhető összes gráfot. Itt a következő élek lehetnek: , , . Ennek megfelelően az alábbi ,,lényegesen különböző'' gráfokat kapjuk: , , , , , . Itt a ,,'' és ,,'' jelek között először a gráf alaphalmaza szerepel, majd a ,,;'' jel után az élek felsorolása. A következő ábrán bemutatjuk ezeket:  I.) Az és gráfoknak nincs szorzata. Ha ugyanis létezik egy morfizmus, akkor alaphalmazának bármely két eleme össze van kötve. Ha pedig egy morfizmus létezik, akkor egyik sem lehet összekötve. II.) Tekintsük most az és gráfok szorzatát, a megfelelő és morfizmusokkal. Mint az előbb láttuk, a gráfban bármely két csúcs össze van kötve. Mivel éltartó, ezért minden csúcsot az csúcsra képez, hiszen a csúcsra csak olyan csúcs lehetne leképezve, amelyik nincs összekötve önmagával. A ,,legkisebb'' ilyen maga az , és az identitás, míg mindegyik csúcsot az csúcsra képezi. Ha most és morfizmusok, akkor ,,szerint'' -ben bármely két csúcs össze van kötve, és így minden csúcsot -ra képez. Eszerint csak az identitás lehet, és az jó is. III.) Az és gráfoknak egészen más okból nincs szorzatuk, mint I.) alatt. Itt ugyanis két jelölt is akad, de ezek ,,összeférhetetlenek''. Mint már láttuk, szorzatnál csak olyan gráf jöhet szóba, amelyikben bármely két csúcs össze van kötve. Ugyanúgy, mint a II.) alatti példában, ekkor vagy csak az csúcsra vagy csak a csúcsra képez. Ilyen gráfok vannak is; például is ilyen, mert akár -ra akár -re képezzük a csúcsokat, a kategória egy-egy morfizmusát kapjuk. Ennek megfelelően, ha tetszőleges morfizmus és minden csúcsot -ba visz, akkor tekintsünk egy gráfot, amelyet leképezünk valahogy -ba (). Eszerint -ben is minden csúcs össze van kötve. Ezért az a leképezés, amely minden csúcsot -be visz ugyancsak hozzátartozik a kategóriához. Ekkor viszont akárhogyan is választjuk a morfizmust, -nél minden csúcs -ra képződik, míg esetében a csúcsok képe lesz. Hasonlóképpen látható be a másik eset lehetetlensége, hiszen és szerepe szimmetrikus. Ezt az esetet a következő diagram szemlélteti:  IV.) Végül nézzük az gráfnak önmagával vett szorzatát. Ez úgy viselkedik, ahogy ,,elvárható''. Csúcsai az , , , párok, bármely két csúcs össze van kötve, és a megfelelő morfizmusok az első, illetve második komponensre való ,,vetítések''. A fenti furcsa helyzet azért adódott, mert a morfizmusokat nem megfelelően választottuk. Tulajdonképpen az objektumok közül is elhagyhatunk, ami ugyancsak ,,patologikus'' helyzetet eredményezne. Vannak ,,elég tisztességes'' kategóriák is, ahol baj van a szorzattal. Nagyon sok esetben azonban a szorzat ,,természetesen'' adódik. Ha a kategória objektumai valamilyen struktúrák, amelyen relációk és műveletek vannak értelmezve, és a morfizmusok a reláció-, illetve művelet-tartó leképezések, akkor a szorzat-struktúra alaphalmaza mindig az alaphalmazok direkt szorzata. A megfelelő reláció bizonyos elemekre pontosan akkor áll fenn, ha minden komponensen fennáll; míg a megfelelő művelet az eredeti műveletek komponensenként való elvégzésével történik. A szorzathoz tartozó morfizmusok pedig az egyes komponensekre való vetítések. Mi most két kategóriát nézünk meg röviden, a kommutatív csoportok kategóriáját és az összes csoport4 kategóriáját. Morfizmusoknak azokat a leképezéseket tekintjük, amelyek művelettartóak, azaz a morfizmusra teljesül. Mindkét kategóriában létezik szorzat, a csoport az adott csoportok direkt szorzata és a morfizmus a megfelelő komponensre való vetítés. Erről nincs sok mondanivalónk; de a diszjunkt unió megfelelőjének tárgyalásánál majd furcsa dolgokat fogunk tapasztalni. A diszjunkt unió a szorzat ,,duálisa'', ennek megfelelően ko-szorzatnak nevezik. Jelölésére a produktum jel ,,fejreállított'' változatát használják. A dualitás abban nyilvánul meg, hogy a nyilak irányítása megfordul. (tehát egy-egy -beli objektum). Ezen objektumok -beli ko-szorzata: diagramok mindegyike kommutatív ( jelöli identitását). A ko-szorzat fenti definíciója azt a szemléletet takarja, hogy ez az a ,,legkisebb'' objektum, amely az adott objektumokat ,,függetlenül'' tartalmazza. A cikk első részében láttuk, hogy a halmazok kategóriájában a ko-szorzat a diszjunkt unió. Könnyen belátható, hogy hasonló a helyzet a gráfok kategóriájában is. Mint már említettük, nem így van a csoportok vagy a kommutatív csoportok esetében. Először nézzük a kommutatív csoportokat, mégpedig additív írásmódban. Legyen és két kommutatív csoport és legyen a direkt szorzat. Ennek elemei tehát alakú párok, ahol , , és a művelet a komponensenként való összeadás. Definiáljuk az és morfizmusokat úgy, hogy tetszőleges , esetén és legyen. Mind mind művelettartó; azt állítjuk, hogy ezzel éppen a ko-szorzatot írtuk le. A definíció első része már megvan. Legyen most és tetszőleges. Definiáljuk a morfizmust úgy, hogy . Ez a leképezés művelettartó, mert Mégse gondoljuk azt, hogy a kommutatív csoportok kategóriájában a szorzat és a ko-szorzat teljesen ugyanaz. A különbséget azonban csak akkor vehetjük észre, ha végtelen sok csoportot tekintünk. Tekintsük az csoportokat (). Ezek szorzatának az elemei olyan végtelen sorozatok, ahol minden egyes az ugyanazon indexű csoportban van. Az összeadást komponensenként végezzük; és az -hez tartozó morfizmus az -edik komponensre való vetítés. Most is megadhatók az morfizmusok, amelyek az -beli elemet abba a sorozatba viszik, amelynek az -edik helyén a megadott elem áll, míg a többi helyen van. Ha most adottak a morfizmusok, akkor a morfizmus csak az lehet, amelyik az sorozatot az összes összegébe viszi. Ennek viszont nincs értelme, mert végtelen sok elemet nem lehet összeadni5. Egyetlen kivétel az, amikor véges sok tag kivételével mindegyik tag . Ebben az esetben teljesen jó felfogás az, hogy csak a -tól különböző tagokat adjuk össze. Erre viszont csak akkor van lehetőségünk, ha a szóbajövő -beli sorozatokban csak véges sok helyen áll -tól különböző elem. És erre van lehetőség! Tekintsük ugyanis -ben azokat a sorozatokat, ahol csak véges sok helyen áll nem- elem. Két ilyen elem összege is ilyen; a csoport -eleme is ilyen, hiszen ebben minden komponens ; és ilyen elem inverze is ilyen, hiszen az inverz elemet a komponensenkénti inverz adja. Eszerint ez egy csoport. Észrevehetjük, hogy az adott morfizmusok nem csak -be, hanem egyszersmind -ba is képeznek, és továbbra is művelettartó módon. Ha mármost -t csak a elemeire definiáljuk, akkor értelmes lesz. Eszerint éppen a ko-szorzat diagram. Kommutatív csoportok ko-szorzata már sokkal előbb ismert volt, mint ahogy a ko-szorzat fogalmát bevezették. Akkor ezt a csoport-struktúrát direkt összegnek nevezték. Ez az elnevezés persze ma is életben van. Végezetül a csoportok kategóriájában nézzük meg a ko-szorzatot. Először azt mutatjuk meg, hogy itt a szorzat nem egyenlő a ko-szorzattal. Az és csoportok szorzatában ‐ mint láttuk ‐ a csoport elemei alakú párok, ahol , . A műveletet komponensenként végezzük és az adott csoportokra való morfizmusok a megfelelő komponensekre való vetítések. Itt is létezik az és morfizmus, amelynél és teljesül6. Ha adott egy és egy morfizmus, akkor egyáltalán nem biztos, hogy ; míg egy megfelelő létezéséből Jelölje 1, 2, 3 egy szabályos háromszög csúcsait. A példában szereplő összes csoport e háromszög egybevágósági transzformációiból fog állni; e transzformációk kompozíciójával mint művelettel. Legyen az identikus transzformáció, az a transzformáció, amelyik az és a csúcsot cseréli fel, az a transzformáció, amelyik az és csúcsot cseréli fel. és . Ezek mindegyike csoport; éppen úgy, mint az összes transzformáció csoportja. és legyen az a morfizmus, amely mindegyik transzformációnak önmagát felelteti meg. Ekkor , míg ; ez a két transzformáció tehát különböző. Az ko-szorzat diagramban a megadása sem túlságosan egyszerű. Tekintsük az alakú ,,szavakat'', ahol , . Ezeket a szavakat bizonyos esetekben ,,rövidíthetjük''. Ha valamilyen esetén , vagy valamilyen esetén , akkor helyébe a -beli , illetve helyée az -beli elemet írjuk. Ha addig végezzük a rövidítéseket, amíg csak lehet, akkor egy ,,rövidíthetetlen'' szóhoz jutunk. Nem túlságosan nehéz, de elég aprólékos munka belátni, hogy a rövidítéseket bármilyen sorrendben végezve mindig ugyanahhoz a szóhoz jutunk. elemei a rövidíthetetlen szavak lesznek. Az és rövidíthetetlen szavak szorzatát a következőképpen kapjuk: Egymás mellé írjuk őket és a kapott szónak vesszük a lerövidített alakját. Egységelem az ,,'' szó lesz, ahol az ,,első'' az -ból, a ,,második'' a -ből való. Az inverzet úgy kapjuk, hogy a ,,betűk'' inverzeit fordított sorrendben írjuk fel; majd az elejére is és a végére is egy-egy -t írunk. Így és . az elemnek az és a elemnek az rövidíthetetlen szót felelteti meg. Ha mármost adott az diagram, akkor a morfizmust a következőképpen definiálhatjuk: Azt kellene még belátni, hogy a csoportok kategóriájának egy morfizmusa. Ebben az egyetlen kellemetlen dolog annak a megmutatása, hogy a fenti hozzárendelés egyértelmű. Ennek a kellemetlenségnek az az oka, hogy egy-egy szót többféle alakban is megadhatunk, és nem eleve biztos, hogy bármilyen alakból indulunk is ki, mindig ugyanaz lesz a kép. Ez a csoportkonstrukció is ismert volt még a ko-szorzat ismerete előtt. Magát a csoportot az adott csoportok szabad szorzatának nevezték. Ez az elnevezés is használatban van. A kategóriákat és a diagramokat ma is elsősorban fogalmi segédeszközöknek tekintik. Nagy szerepük van a ,,dolgok'' precíz megfogalmazásában és ,,átértésében''. Ahol ,,elvi'' vizsgálatok folynak, ott szinte kivétel nélkül ezt a nyelvet használják. Igen fontosak a matematikai logikában és az elméleti számítástechnikában is. Vannak olyan nem kategóriaelméleti eredmények is, amelyeket először kategóriaelmélet segítségével sikerült bizonyítani.
1Nem igazán fontos, hogy minden esetben tudjuk, mik azok a dolgok, amiket itt megjegyeztünk; csak az a lényeg lássuk, hogy számos olyan matematikai objektum-fajta van, amelyekből igen sok áll rendelkezésünkre.2Tartozom az igazságnak azzal, hogy bevalljam, nem vagyok egészen biztos abban, hogy ezt az ,,elnevezést'' a kategóriaelméletre vagy az univerzális algebrára alkalmazták; de bármelyikük ,,kiérdemelte'' ezt az elnevezést.3Irányítatlan gráf egy nem üres halmaz, ellátva ,,élekkel''. A halmaz elemeit a gráf csúcsainak nevezzük. Bizonyos csúcspárok ki vannak jelölve; ha egy csúcspár ki van jelölve, akkor azt mondjuk, hogy e csúcsok össze vannak kötve éllel, egyébként nincsenek. A gráfot egyértelműen meghatározza a csúcsok és az élek halmaza. A csúcsok halmazát a gráf tartóhalmazának nevezzük. A gráffal együtt a tartóhalmazt is -vel jelöljük.4Csoporton a következőket értjük: Adott egy halmaz, amelyen értelmezve van egy szorzásnak nevezett művelet; és szorzatát jelöli. A szorzás asszociatív. Léteznie kell egy egységelemnek, amire tetszőleges esetén 1a=a1=a; továbbá minden elemhez kell lennie egy inverznek ‐ amit jelöl ‐, amire . Ha a szorzás kommutatív, akkor kommutatív csoportról beszélünk. Ez esetben sokszor ,,'' jelöli a műveletet, aminek a neve összeadás; az egységelem jele , és inverzét jelöli. E mellett a jelölés mellett additív írásmódról beszélünk.5Az összeadást eleve csak két elemre értelmeztük. Az asszociativitást felhasználva akármennyi ‐ de véges sok ‐ elemre értelmezhető és egyértelmű az összeadás. A soroknak a határérték felhasználásával definiált összegéről itt nem beszélhetünk, mert itt általában nem létezik határérték.6Most nem használjuk az additív írásmódot, mert a szorzás kommutativitását nem tesszük fel. |