Kezdőlap


Cím:	Gráfmodellek
Szerző(k):	Farkas Gyula
Füzet:	1997/március, 137 - 145. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Bevezetés
Számos gyakorlatban felmerülő probléma vizsgálata során segítséget nyújthat, ha átfogalmazzuk gráfelméleti feladattá, azaz kölcsönösen egyértelmű kapcsolatot létesítünk a gráfelméleti feladat megoldása, és a konkrét probléma megoldása között. Ez nemcsak azért hasznos, mert áttekinthetőbbé, matematikailag kezelhetőbbé válik a problémánk, hanem azért is, mert első látásra különböző problémák vezethetnek ugyanarra a feladatra. A továbbiakban az általunk választott feladat a színezés lesz. Mielőtt összefoglalnánk a szükséges alapismereteket, definíciókat, és azt, hogy pontosan mit is értünk színezésen, lássunk egy-két példát gráfokra. Ha megérkezünk egy társaságba, rögtön felmérjük, kit ismerünk, és kit nem. Eredményünket a síkon igen szemléletesen ábrázolhatjuk. Bizonyos pontokat (hívjuk őket csúcsoknak) a jelenlévő emberekhez rendelünk, és két csúcsot összekötünk, ha a hozzájuk rendelt emberek ismerik egymást. Gráffal ábrázolhatjuk például egy jégkorongbajnokságban a különböző csapatok mérkőzéseit. Minden csapatnak megfeleltetünk egy pontot, két pontot annyi él köt össze, ahányszor a két csapat játszott egymással. A győztesnek megfeleltetett pontból a vesztesé felé vezető él végére nyilat rajzolunk. (A döntetlent most nem engedjük meg.)

2. Definíciók

Induljuk ki egy

V

véges halmazból; ennek elemei lesznek a gráf csúcsai. Az

i

és

j

csúcsokat összekötő élt megfeleltetjük az

[i, j]

párnak, az így kapott párok felsorolását jelöljük

E

-vel. Egy

[i, j]

pár annyiszor eleme

E

-nek, ahány él összeköti

i

-t és

j

-t. (Emiatt

E

nem feltétlenül halmaz.) Szokásos még

[i, j] \in E

esetén az

i

és

j

szomszédos csúcsokról, vagy

e = [i, j]

jelölés esetén az

e

élre illeszkedő csúcsokról beszélni. E jelöléssel az

e

él végpontjai

i

és

j

. Két él szomszédos, ha van közös végpontjuk.
A

G = (V, E)

gráf egyszerű, ha nincs olyan éle, amelynek végpontjai azonosak (hurokél), és tetszőleges két csúcsát nem köti össze egynél több él (nincs többszörös éle

G

-nek). Ez utóbbi feltétel azt biztosítja, hogy

E

is halmaz lesz, hiszen nem lesz két különböző él azonos végpontokkal.
A

G = (V, E)

gráf részgráfja a

H = (V', E')

gráf, ha

V' \subseteq V

E' \subseteq E

úgy, hogy

E'

elemeinek végpontjai benne vannak

V'

-ben. Ezt a feltételt azért követeljük meg, mert egyébként előfordulhatna az, hogy egy él valamely végpontja nem tartozna a részgráfhoz.
A

\vec{G} = (V, \vec{E})

gráf irányított, ha

\vec{E}

elemei rendezett párok. Az irányítatlan gráf éleitől eltérően

(i, j)

-vel jelöljük

\vec{E}

elemeit, és

(i, j) \in \vec{E}

esetén

i

-ből

j

-be mutató élről beszélünk. Az

e = (i, j)

jelölés esetén az

e

él kezdőpontja

i

, végpontja

j

.
Legyen

i_{0}

i_{1}

...

i_{k} \in V

és

e_{1}

e_{2}

...

e_{k} \in E

. Az

(i_{0}, e_{1}, i_{1}, e_{2}, i_{2}, ..., i_{k - 1}, e_{k}, i_{k})

sorozatot sétának nevezzük, ha

e_{j}

i_{j - 1}

-et és

i_{j}

-t összekötő él minden

j = 1

2

...

k

esetben. Ha

i_{0} = i_{k}

, akkor a séta zárt. Ha a csúcsok mind különbözők, akkor a séta neve út. Ha ezen kívül zárt is, akkor ez egy kör a gráfban. Az út vagy a kör hosszán az őt alkotó élek számát értjük. Irányított gráfokban hasonló módon definiálható az irányított út és az irányított kör fogalma.
Az

i

csúcs foka a

G

gráfban az

i

-re illeszkedő élek száma. Jele:

d_{G} (i)

. A

G

gráf

d

-reguláris, ha

d_{G} (i) = d

minden

i

csúcsra. Egy

i

csúcs

G

-beli szomszédainak halmazát jelölje

M_{G} (i)

.
Álljon

F

G

gráf bizonyos éleiből.

F

párosítás, ha nem tartalmaz szomszédos éleket. Ha

G

éleit felbontjuk diszjunkt párosításokra, akkor

G

egy élszínezését kapjuk. Szemléletesen ez azt jelenti, hogy az éleket kiszínezzük néhány színnel úgy, hogy minden csúcsra csupa különböző színű él illeszkedjen. Az azonos színű élek alkotják a párosításokat, hiszen minden élt csak egy színnel színeztük (nincs tarka él) épp úgy, hogy két azonos színű ne lehessen szomszédos.
Ha az

F

olyan párosítás, amelyben a benne szereplő élek végpontjai kiadják

V

-t, röviden, ha

F

1-reguláris, akkor

F

neve: faktor.

G

éleinek felbontása diszjunkt faktorokra a faktorizáció.

3. Sportversenyek lebonyolítása

Bizonyos sportágak bajnokságát körmérkőzéses formában bonyolítják le. Ez azt jelenti, hogy a bajnokság több fordulóból áll, egy-egy fordulóban bármely két csapat legfeljebb egyszer játszik, a bajnokság végére viszont bármely két csapat pontosan egyszer megmérkőzik egymással. Feladatunk megszervezni

n

csapat körmérkőzéses bajnokságát úgy, hogy az a lehető legkevesebb fordulóból álljon. A fordulók számát minimalizálni könnyű lesz, maga a lebonyolítás pedig faktorizációs problémához vezet.
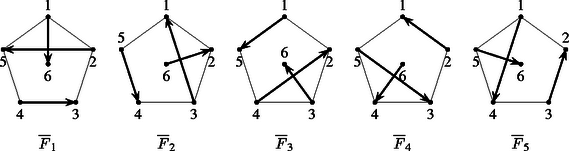
Legyen

n

páros, a páratlan

n

esetét majd erre vezetjük vissza. Készítsük el a következő gráfot. Minden csapatnak feleltessünk meg egy csúcsot, majd a kapott

n

csúcs között húzzunk be minden lehetséges élt. Az így kapott gráfot

K_{n}

-el jelöljük, és

n

csúcsú teljes gráfnak hívjuk. Könnyű látni, hogy

K_{n} (n - 1)

-reguláris. Tekintsük

K_{n}

egy élszínezését; a különböző színű élek halmazait jelöljük

M_{1}

M_{2}

...

M_{d}

-vel, ahol

M_{1}

az ,,1''-színű,

M_{2}

a ,,2''-színű,

...

M_{d}

a ,,

d

''-színű élek halmaza. Most már kapható egy sportverseny-lebonyolítás úgy, hogy ha

[i, j] \in M_{p}

, akkor az

i

és a

j

csapat a

p

-edik napon (fordulóban) mérkőzik. Páros

n

esetén

d

elméletileg elérhető minimuma

n - 1

(

K_{n}

tetszőleges élszínezése esetén

d \geq n - 1

, hiszen van olyan csúcs (mind), amelynek foka

n - 1

, azaz

n - 1

különböző színre mindenképpen szükség van), ekkor minden fordulóban minden csapat játszik. Gráfnyelvre lefordítva

K_{n}

élszínezését keressük

n - 1

színnel, ami nem más, mint

K_{n}

faktorizációja, ahol az

i

-edik faktorba eső éleket színezzük az ,,

i

'' színnel. Páros

n

esetén viszont

K_{n}

faktorizálható, ez egy konkrét faktorizáció előállításából azonnal látszik. Jelöljük

K_{n}

csúcsait az

1

2

...

n

számokkal. Az első

n - 1

csúcsot rakjuk le egy szabályos

(n - 1)

-szög csúcsaira, az utolsót pedig a szimmetria-középpontra. Az első faktor legyen a következő: kössük össze az

1

-es csúcsot a szimmetria-középpontban lévő

n

-es csúccsal, a

2

-est az

(n - 1)

-essel, a

3

-ast az

(n - 2)

-essel, stb

...

Az összes többi faktort úgy kapjuk, hogy mindig elforgatjuk az előző ábrát a szimmetria-közzéppont körül

360^{\circ} / n

fokkal (a számozás marad).

K_{6}

előző faktorizációját láthatjuk az 1. ábrán (most még ne zavarjanak az irányított élek). Akik matematikailag pontosabban is szeretnék megfogalmazni az állítást, azok számára megjegyezzük, hogy

F_{i}

(az

i

-edik faktor) felírható a következő alakban:

\begin{matrix} F_{i} = {[n, i]} \cup {[i + k, i - k] ∣ k = 1, 2, ..., (n / 2) - 1}, \end{matrix}

ahol az

i + k

, illetve az

i - k

értékek modulo

(n - 1)

értendőek.
Páratlan

n

esetén vegyünk fel egy fiktív csapatot, végezzük el az előző faktorizációt, majd a sportverseny-lebonyolítást úgy kapjuk, hogy fordulóként a fiktív csapattal összekerült csapat pihen. Így páratlan

n

esetén egy

n + 1

fordulós bajnokságot kapunk, és könnyen látható, hogy jobbat nem is várhatunk.
Valamivel érdekesebbé tehetjük a feladatunkat, ha figyelembe vesszük a hazai, illetve vendég mérkőzéseket. Gráfmodellünkben ezt úgy tehetjük meg, hogy az

[i, j]

éleket kicseréljük

(i, j)

irányított élekre, és egy

(i, j)

él esetén azt mondjuk, hogy

i

vendég mérkőzést játszik

j

otthonában. Így, ha már van egy élszínezésünk, akkor még irányítanunk is kell valahogy az éleket. Ezt irányított élszínezésnek hívjuk, és

\vec{M_{1}}

\vec{M_{2}}

...

\vec{M_{d}}

-vel jelöljük. Ezek után könnyen elképzelhető, hogy mit jelent az irányított faktorizáció. Egy irányított élszínezés a konkrét verseny-lebonyolítást hasonlóan definiálja, mint az előbbi esetben, itt ha

(i, j) \in \vec{M_{P}}

, akkor az

i

vendég mérkőzést játszik

j

otthonában a

p

-edik fordulóban. Adott lebonyolítás esetén kitölthetünk egy táblázatot (a Hazai‐Vendég Mérleg-et, a továbbiakban HVM),

2 n

csapat esetén

2 n \times (2 n - 1)

-es lesz, a sorok a csapatoknak, az oszlopok a fordulóknak felelnek meg, és az

i

-edik sor

k

-adik helyére V-t, H-t írunk, ha az

i

-edik csapatnak a

k

-adik fordulóban vendég, hazai mérkőzése van, vagy 0-t, ha ekkor pihen. Állapodjunk meg a következő jelölésekben: jelölje

S

a lebonyolítást, az

S

-hez tartozó HVM jele

H (S)

, az elemeit pedig

h_{i k} (S)

jelöli. Az

i

csapat idénye a

H (S)

i

-edik sora.
A csapatok nem szeretik, ha idényükben egymás után ugyanolyan betű áll, azaz ha két egymást követő forduló mindegyikében hazai vagy vendég mérkőzést kell játszaniuk. Így feladatunk ‐ a csapatok beleegyezésével ‐ az, hogy a faktorizáció után az egyes faktorokban lévő éleket úgy irányítsuk, hogy a fenti nem kívánt előfordulások számát minimalizáljuk. A könnyebb hivatkozás kedvéért, ha

h_{i k} (S) = h_{i, k + 1} (S) = H

vagy V, akkor azt mondjuk, hogy az

i

-edik csapatnak kritikus mérkőzése van a

(k + 1)

-edik fordulóban. Az előbbi fogalmak szemléltetésére

K_{6}

egy irányított faktorizációja látható az 1. ábrán, a táblázatban pedig az ehhez tartozó HVM, ahol a kritikus mérkőzéseket aláhúztuk.

\begin{matrix} 1. forduló & 2. forduló & 3. forduló & 4. forduló & 5. forduló \\ 1. csapat & V & H & V & H & V \\ 2. csapat & V & H & H̲ & V & H \\ 3. csapat & H & V & V̲ & H & V \\ 4. csapat & V & H & V & H & H̲ \\ 5. csapat & H & V & H & V & V̲ \\ 6. csapat & H & V & H & V & H \end{matrix}

A kritikus mérkőzések számára alsó becslés elég könnyen adható, ehhez szükségünk van még egy gráfelméleti fogalomra. A

G

gráf csúcsaiból álló halmazt függetlennek mondjuk

G

-ben, ha nem tartalmaz szomszédos csúcsokat. Jelölje

α (G)

a független

G

-beli halmazoknak a maximális méretét. Az ígért becslés a következő:

Tétel. Legyen

G d

-reguláris, faktorizálható,

2 n

csúcsú gráf. Ekkor tetszőleges irányított faktorizációjához (

\vec{F_{1}}

\vec{F_{2}}

...

\vec{F_{d}}

-hez) tartozó kritikus mérkőzések száma legalább

2 (n - α (G))

Bizonyítás. (i) Először azt látjuk be, hogy legfeljebb

α (G)

csapatnak azonos az idénye. Tegyük fel, hogy

T > α (G)

csapatnak azonos az idénye. Mivel

T

számú csúcs között biztos van két szomszédos, mondjuk

i

és

j

, így lesz

i

j

mérkőzés, azaz valamilyen

k

-ra

h_{i k} (S) \neq h_{j k} (S)

. (Ha egy

i

‐

j

mérkőzés az egyik csapatnak hazai, akkor a másiknak vendég.) Ez viszont ellentmondás, azaz

α (G) \geq T

.
(ii) Legfeljebb

2 α (G)

csapatnak lehet kritikus mérkőzések nélküli idénye, hiszen (i)-ből adódóan legfeljebb

α (G)

csapat van, melynek idénye H-val kezdődik és nincs kritikus mérkőzése, hasonlóan legfeljebb

α (G)

csapat van, melynek idénye V-vel kezdődik és nincs kritikus mérkőzése.
(iii) Így már adódik, hogy legalább

2 n - 2 α (G) = 2 (n - α (G))

idény van legalább egy kritikus mérkőzéssel, ebből viszont következik az állítás.

Következmény.

K_{2 n}

tetszőleges

(\vec{F_{1}}

\vec{F_{2}}

...

{\vec{F}}_{2 n - 1})

irányított faktorizációjához tartozó kritikus mérkőzések száma legalább

2 n - 2

K_{6}

esetén ez a szám

4

, és mint látható a táblázatban, az általunk adott faktorizációhoz éppen

4

kritikus mérkőzés tartozik, tehát optimális abban az értelemben, hogy kevesebb kritikus találkozóval nem lehet

6

csapat bajnokságát lebonyolítani.

4. Egy feladatkiosztási probléma

Tegyük fel, hogy

m

munkással dolgoztatunk. Jelöljük őket

P_{1}

P_{2}

...

P_{m}

-mel, halmazukat P-vel. A munkásokkal el kell végeztetnünk

n

munkát, jelük legyen

J = (J_{1}, J_{2}, ..., J_{n})

. Minden munka részfeladatokra van felosztva a munkásoknak megfelelően, azaz bármely

J_{j}

munka

T_{1 j}

T_{2 j}

...

T_{m j}

részekre osztott, ahol a

T_{i j}

részt csak a

P_{i}

munkás végezheti el. Tegyük még fel, hogy az előbbi

T_{i j}

feladatot a

P_{i}

munkás

p_{i j}

idő alatt végzi el, ahol

p_{i j}

egész. (Ha valamely

p_{i j}

nulla, akkor azt mondjuk, hogy a megfelelő

T_{i j}

nem létezik.) A feltételekhez tartozik még, hogy egy adott munka részfeladatait nem végeztethetjük el egyszerre, valamint egy munkás egyidőben csak egy részfeladattal foglalkozhat. Az első feltételt úgy magyarázhatjuk, hogy csak egy munkaállomással rendelkezünk munkánként, így egyidőben csak egy munkás dolgozhat. Feladatunk ezek után az, hogy minél rövidebb idő alatt végezzünk az összes munkával.
Gráfmodellt ebben az esetben is könnyű adni. Legyenek a csúcsok a munkások és a munkák, jelöljük

P_{i}

, illetve

J_{j}

-vel. Ha egy

T_{i j}

részfeladat elvégzésének ideje

p_{i j}

, akkor húzzunk be

p_{i j}

darab

[P_{i}, J_{j}]

élt.
Ha most tekintünk egy élszínezést,

M_{1}

M_{2}

...

M_{d}

-t, akkor definiálható egy

d

idejű megoldás a következő módon: az első időegység elején kezdjük el az

M_{1}

-beli éleknek megfelelő részmunkákat, a második időegység elején az eddigieket félbeszakítjuk, majd az

M_{2}

-beli éleknek megfelelőeket kezdjük el, stb

...

Így a két feltételt valóban nem sértjük meg, de olyan eset előfordulhat, hogy egy munkás nem fejezi be teljes egészében a ráosztott feladatot, hanem egy másikba kezd, majd később visszatér a félbehagyotthoz. Ezt persze nem is tiltottuk meg. Nézzük meg figyelmesebben a modellezés során nyert gráfot. A csúcsait két diszjunkt halmazba sorolhatjuk úgy, hogy a halmazokba eső csúcsok között él nem vezet. Az ilyen struktúrájú gráfok neve: páros gráf. Már a 3. pontban is felhasználtuk azt az egyszerű tényt, hogy egy gráf élszínezésének mérete legalább akkora, mint a maximális fokszáma (jele:

Δ (G)

). Páros gráfok esetében viszont többet is mondhatunk:

König-tétel. Ha

G

páros gráf, akkor létezik élszínezése

Δ (G)

színnel.
Vagyis feladatunk megoldható

Δ (G)

idő alatt (ennél gyorsabban nem is lehet), sőt az is igaz, hogy egy ilyen feladatkiosztást ,,gyorsan'' találhatunk.

Δ (G)

felírható

p_{i j}

-k segítségével a következő módon:

Δ (G) = {max}_{}^{} {{max}_{g}^{} \sum_{j} p_{g j}, {max}_{j}^{} \sum_{g} p_{g j}}

.
Érdekesebb lehet a feladat, ha figyelembe vesszük a munkabéreket, vagy más költségeket. Ekkor ésszerű kérés, hogy ne csak gyorsan, de olcsón is végezzünk az összes munkával.
Hogy a fenti problémát matematikailag leírjuk, jelöljük

c_{i}

-vel az

i

-edik időegység átlagos költségét, azaz az összes költség az

i

-edik időegység alatt

c_{i} | M_{i} |

, ahol

| M_{i} |

i

-edik időegység alatt végzett munkák száma (az ,,

i

'' színű élek száma

G

-ben). Így ha

M_{1}

M_{2}

...

M_{k}

egy élszínezés, akkor az ehhez tartozó

S

megoldás (ütemezés) összköltsége:

\sum c_{i} | M_{i} |

.
Egy

G = (V, E)

hurokél mentes gráf esetén egy

H = (h_{1}, h_{2}, ..., h_{k})

nemnegatív egészekből álló sorozatot szín-megengedettnek hívunk, ha

h_{1} \geq h_{2} \geq ... \geq h_{k}; \sum h_{i} = | E |

és létezik

k

színű élszínezése

G

-nek,

M_{1}

M_{2}

...

M_{k}

úgy, hogy

| M_{i} | = h_{i}

i = 1

2

...

k

esetén.
Két sorozatot összehasonlíthatunk: legyenek

H = (h_{1}, h_{2}, ..., h_{k})

H' = (h'_{1}, h'_{2}, ..., h'_{k})

szín-megengedettek

G

-ben.

H \geq H'

, ha

h_{1} + h_{2} + ... + h_{j} \geq h'_{1} + h'_{2} + ... + h'_{j}

teljesül minden

j = 1

, 2,

...

k

esetén.
Legyen

C (G)

G

-beli szín-megengedett sorozatok halmaza. Mivel

h_{i}

értéke

0

is lehet,

k

értékét minden sorozat esetén vehetjük

| E |

-nek (az élek számának). Ekkor

| C (G) | < \infty

. Egy

H \in C (G)

maximális, ha nincs olyan

H' \in C (G)

, hogy

H' \neq H

és

H' \geq H

.
Érdemes megemlíteni a következő állítást:

Tétel. Ha

H \in C (G)

és

H \geq H'

, akkor

H' \in C (G)

.
A 2. ábrán látható gráfnak (amelyről könnyen belátható, hogy páros gráf) kétféle élszínezését ábrázoltuk a 3. ábrán (ahol a számok különböző színeket jelentenek). A megfelelő sorozatok:

H = (5,2,2)

és

H' = (4,4,1)

. A fenti tételből adódik, hogy

(4,3,2)

és

(3,3,3)

is szín-megengedett, hiszen

(4,3,2) \leq H

és

(3,3,3) \leq (4,3,2)

.
Tegyük fel, hogy a költségek rendezettek:

c_{1} \leq c_{2} \leq ... \leq c_{k}

. Ez a feltevés nem jelenti az általánosság megszorítását.

Tétel. A

c (H) = \sum c_{i} h_{i}

minimális értékét olyan

H \in C (G)

esetén veszi fel, ami maximális.

Bizonyítás. Legyen

H' \in C (G)

olyan, ami nem maximális. Ekkor létezik

H \in C (G)

maximális úgy, hogy

H \geq H'

. Egyrészt

\begin{matrix} \sum c_{i} h'_{i} = c_{1} (h'_{1} + h'_{2} + ... + h'_{k}) + (c_{2} - c_{1}) (h'_{2} + h'_{3} + ... h'_{k}) + ... + (c_{k} - c_{k - 1}) h'_{k} . \end{matrix}

(*)

Valamint

H \geq H'

miatt

\begin{matrix} \begin{matrix} h_{1} & \geq h'_{1} \\ h_{1} + h_{2} & \geq h'_{1} + h'_{2} \\ ⋮ \\ h_{1} + h_{2} + ... + h_{k} & = h'_{1} + h'_{2} + ... + h'_{k} . \end{matrix} \end{matrix}

Kivonva rendre minden egyenlőtlenséget az utolsó egyenletből, azt kapjuk, hogy

\begin{matrix} \begin{matrix} h'_{2} + h'_{3} + ... + h'_{k} & \geq h_{2} + h_{3} + ... + h_{k} \\ h'_{3} + h'_{4} + ... + h'_{k} & \geq h_{3} + h_{4} + ... + h_{k} \\ ⋮ \\ h'_{k} & \geq h_{k} . \end{matrix} \end{matrix}

Ezeket az egyenlőtlenségeket

(*)

-ba helyettesítve (

(c_{i} - c_{i - 1}) \geq 0

miatt):

\begin{matrix} \begin{matrix} \sum c_{i} h'_{i} & \geq c_{1} (h_{1} + h_{2} + ... + h_{k}) + (c_{2} - c_{1}) (h_{2} + h_{3} + ... + h_{k}) + ... + (c_{k} - c_{k - 1}) h_{k} = \\ = \sum c_{i} h_{i} . \end{matrix} \end{matrix}

Tehát azt kaptuk, hogy nem maximális sorozat nem lehet minimális költségű, ez pedig ekvivalens a tétel állításával.
E tétel alapján tehát elég lenne az összköltség minimalizálásához

C (G)

-ben maximális sorozatot keresni. Viszont lehet több maximális sorozat is

C (G)

-ben, például a 3. ábrán látható

(5,2,2)

és

(4,4,1)

mindegyike maximális. Sőt,

(c_{1}, c_{2}, c_{3}) = (0,1,3)

költségek esetén a minimális összköltség a

(4,4,1)

sorozat esetén adódik, míg

(c_{1}, c_{2}, c_{3}) = (0,2,3)

költségek esetén pedig

(5,2,3)

-nál.

5. Frekvencia-hozzárendelés

Az újabb problémák megoldásához szükségünk lesz a gráfszínezések egy újabb csoportjának megismerésére. Eddig a gráfunk éleit színeztük, most viszont áttérünk a csúcsok színezésére. Egy színezést akkor tekintünk ,,jó''-nak, ha minden szomszédos csúcspár különböző színt kap. Ezt valamivel precízebben is megfogalmazhatjuk. Legyen

G

egy irányított gráf. Az

f : V \to {1, 2, ..., k}

függvényt a

G

gráf klasszikus (

k

-színű) színezésének mondjuk, ha

G

minden

(i, j)

irányított élére teljesül, hogy

\begin{matrix} f (j) - f (i) \neq 0. \end{matrix}

(1)

Ezt az egyszerű definíciót általánosítva eljutunk egy olyan színezés definícióhoz, ami használható lesz a vizsgálandó problémánk szempontjából. Először is minden

(i, j)

élhez rendeljünk egy

T_{i j}

-vel jelölt, egészekből álló halmazt úgy, hogy minden

T_{i j}

tartalmazza a nullát. Az előbbi definíció általánosításaként

k

-színű

T

-színezésről beszélünk, ha az előbbi

f

függvényre

(1)

helyett

\begin{matrix} f (j) - f (i) \notin T_{i j} \end{matrix}

(2)

teljesül

G

minden

(i, j)

élére. Vegyük észre, hogy ha minden

T_{i j} = {0}

, akkor a

T

-színezés egybeesik a klasszikus színezéssel.
Rendeljünk minden

i

csúcshoz egy

c_{i}

pozitív egészt. Tegyük fel, hogy az

(i, j)

élekhez rendelt

T_{i j}

halmazokra teljesül, hogy

\begin{matrix} {- c_{j} + 1, - c_{j} + 2, ..., c_{i} - 2, c_{i} - 1} \subseteq T_{i j} . \end{matrix}

(3)

Ilyen feltételek mellett a

T

-színezést intervallum

T

-színezésnek hívjuk. Az elnevezés magyarázata az a szemléletes kép, hogy ha minden

i

csúcshoz

c_{i}

egymás utáni színt rendelünk, akkor szomszédos csúcsok színei között nem lesznek azonosak. Abban az esetben, amikor minden csúcshoz az

1

számot rendeljük, visszakapjuk a

T

-színezést, hiszen a

(3)

feltétel a

{0} \subseteq T_{i j}

feltétellé redukálódik.
Visszatérve a gyakorlati kérdésekre, megfogalmazhatunk két olyan problémát is, melyek a lehető legkevesebb színű intervallum

T

-színezések megkeresésére vezethetők vissza.
Az első probléma hasonlít a munkakiosztási feladathoz, viszont itt más feltételeket szabunk. Legyen J az elvégzendő munkák halmaza. Jelölje

c_{i}

i

munka elvégzésének idejét. Bizonyos

i, j

párok nem végezhetők egyszerre, míg más

i, j

pároknál olyan feltételt írunk elő, hogy

j

megkezdése előtt

i

-nek be kell fejeződnie. Feltétel még, hogy ha elkezdünk egy munkát, akkor azt be is kell fejezni. A feladat ezek után az, hogy a lehető legrövidebb idő alatt elvégezzük az összes munkát a feltételek megtartása mellett.
A modellt a következő módon gyártjuk: minden

i

munkának feleltessünk meg egy csúcsot, és lássuk el a

c_{i}

értékkel. Ha

i

és

j

nem végezhető egyszerre, akkor húzzunk be egy

(i, j)

élt, és ahhoz rendeljük hozzá a

T_{i j} = {- c_{j} + 1, ..., c_{i} - 1}

halmazt. Ha

j

csak akkor végezhető, ha

i

befejeződött, akkor húzzunk be ugyancsak egy

(i, j)

élt, de a

\begin{matrix} T_{i j} = {- M, - M + 1, ..., c_{i} - 1} \end{matrix}

halmazzal, ahol

M

egy ,,elegendően'' nagy (pozitív) szám (pl:

M = \sum c_{i}

). Könnyen látható, hogy kölcsönösen egyértelmű kapcsolatot létesíthetünk az előbb konstruált gráf

k

-színű intervallum

T

-színezése, és az eredeti probléma

k

időegység alatti ütemezése között. Sőt, az is könnyen adódik, hogy e gráfnak pontosan akkor létezik intervallum

T

-színezése, ha azon

(i, j)

élek, amelyekre

T_{i j} = {- M, - M + 1, ..., c_{i} - 1}

, nem alkotnak irányított kört.
A kapott modellt kis módosítással általánosabb probléma esetén is használhatjuk. Tegyük fel ugyanis, hogy

j

csak akkor kezdhető, ha

i

befejezése után legalább

p

idő eltelt (például meg kell száradnia a festéknek). A modellt úgy módosítjuk ebben az esetben, hogy felveszünk egy fiktív

f

csúcsot

c_{f} = p

értékkel, valamint behúzzuk az

(i, f)

és az

(f, j)

éleket a

T_{i f} = {- M, ..., c_{i} - 1}

és a

T_{f j} = {- M, ..., p - 1}

halmazokkal.
Érdemes megjegyezni, hogy ha a modellként kapott gráf csak olyan

(i, j)

éleket tartalmaz, amelyekre

T_{i j} = {- M, ..., c_{i} - 1}

, akkor a legkisebb intervallum

T

-színezés megtalálása visszavezethető az úgynevezett leghosszabb út keresésre. Nem túl precízen fogalmazva ezt úgy kell elképzelni, hogy minden élre rá van írva a ,,súlya'', a mi esetünkben egy

(i, j)

él súlya

c_{i}

lesz, és egy út súlyát a benne szereplő élek súlyainak összege definiálja. A leghosszabb út keresés az a feladat, hogy minden

i

csúcsra meghatározzuk az

i

végpontú utak közül a leghosszabbat. Ha ezt megoldottuk, akkor egyszerűen kapható a megfelelő intervallum

T

-színezés, ugyanis az

i

csúcshoz rendelt

f (i)

legyen a leghosszabb út hossza.
A következő problémához tegyük fel, hogy rendelkezünk erősítők egy

V

halmazával, valamint lehetséges frekvenciákkal, melyeket egész számokkal reprezentálunk. Feladatunk a frekvenciákat úgy hozzárendelni az erősítőkhöz, hogy a nem kívánt interferenciákat elkerüljük. A legegyszerűbb esetben a frekvenciákat

50

kHz-es egységekben számoljuk, és a következő két feltételt követeljük meg:

(a) Ha két erősítő közel van egymáshoz, akkor frekvenciájuk között legalább

50

kHz-nyi különbségnek kell lenni.
(b) Ha két erősítő nagyon közel van egymáshoz, akkor a különbségnek legalább

100

kHz-nek kell lenni.

A problémához tartozó gráfban az erősítők felelnek meg az csúcsoknak. Az (a) esetben behúzunk egy

(i, j)

élt

T_{i j} = {0}

halmazzal, a (b) esetben pedig ugyancsak egy

(i, j)

élt, de

T_{i j} = {- 1,0,1}

halmazzal. Legyen még minden

i

csúcsra

c_{i} = 1

. Most is könnyen leellenőrizhető a kölcsönösen egyértelmű kapcsolat e gráf

k

-színű intervallum

T

-színezései, valamint az eredeti probléma olyan megoldása között, ahol az előforduló legnagyobb frekvencia legfeljebb

50 k

kHz. Ha tehát a legnagyobb előforduló frekvenciát a lehető legkisebbre akarjuk választani, akkor itt is a legkisebb intervallum

T

-színezés megkeresése a feladat.
Egy speciális esetben a lehető legkevesebb színt használó intervallum

T

-színezés megkeresése viszonylag egyszerűen megoldható. A speciális eset megfogalmazásához szükségünk lesz egy fogalomra:

Definíció. Egy

G = (V, E)

gráf indukált részgráfja a

H = (V', E')

gráf, ha részgráfja, valamint

E'

azokból az

E

-beli élekből áll, amelyeknek mindkét végpontja

V'

-ben van, és

E'

az összes ilyen élt tartalmazza.
Szemléletesen ez azt jelenti, hogy az eredeti gráf bizonyos csúcsait tekintem csak, viszont ezen csúcsokra illeszkedő valamennyi

G

-beli élt. A speciális eset mármost a következő: legyen

G

olyan egyszerű gráf, mely nem tartalmaz

4

csúcson áthaladó, azaz

3

hosszú utat (jele:

P_{4}

), indukált részgráfként. Ekkor igaz a következő állítás:

Tétel. A fenti tulajdonságú

G

gráf minden nemtriviális (azaz nem csak egy pontból álló)

H

részgráfjának vagy van két olyan

i

és

j

csúcsa, melyek szomszédosak, és

M_{H} (i) - {y} = M_{H} (j) - {i}

(egypetéjű ikrek), vagy van két olyan

i

és

j

csúcsa, melyek nem szomszédosak, és

M_{H} (i) = M_{H} (j)

(kétpetéjű ikrek).
E tétel alapján meghatározhatjuk a legkisebb intervallum

T

-színezést. Futtassuk le a következő algoritmust:

(1. lépés) Megvizsgáljuk, hogy a

G

gráf triviális-e. Ha igen, akkor befejezzük az algoritmust, ha nem, akkor ugrunk a 2. lépésre.
(2. lépés) A tétel alapján választhatunk

G

-ből egy

i

j

ikerpárt.
(3. lépés) Ha egypetéjű ikerpárt sikerült választanunk, akkor a

j

-hez tartozó új

c_{j}

legyen

c_{i} + c_{j}

. Ellenkező esetben legyen

c_{j} = {max}_{}^{} (c_{i}, c_{j})

.
(4. lépés) Az új

G

gráfot úgy kapjuk, hogy töröljük

G

-ből az

i

csúcsot a rá illeszkedő élekkel együtt. Ezután visszaugrunk az 1. lépésre.

Az algoritmus lefutása után marad egyetlen

z

csúcs valamilyen

c_{z}

értékkel. Ekkor található egy

c_{z}

-színű intervallum

T

-színezés, mégpedig úgy, hogy ,,visszafelé'' futtatjuk az algoritmust (ezt úgy tehetjük meg könnyedén, ha a futás során feljegyezzük, hogy az ikerpárok mely tagját töröltük, a régi

c_{i}

értékkel együtt). Ha egy

z

csúcs az egypetéjű

i

j

ikerpárból keletkezett, akkor

z

-t felbontjuk az

i

és a

j

csúcsokra úgy, hogy

i

kapja az első

c_{i}

j

pedig az utolsó

c_{j}

színt. Ha

z

i

j

kétpetéjű ikerpárból keletkezett, akkor

z

-t szintén felbontjuk

i

-re és

j

-re, viszont

i

illetve

j

mindegyike az első

c_{i}

illetve

c_{j}

színt kapja (kaphatja, hiszen a kétpetéjű ikrek nem szomszédosak).

Feladatok

1. Bizonyítsuk be, hogy

K_{2 n}

esetén mindig van olyan irányított faktorizáció, amelyhez tartozó kritikus meccsek száma éppen

2 n - 2

2. Miért maximálisak az

(5, 2, 2)

és

(4, 4, 1)

sorozatok?

3. Bizonyítsuk be, hogy a feladatkiosztási problémához konstruált gráfra:

\begin{matrix} Δ (G) = {max}_{}^{} {{max}_{}^{}_{g}^{} \sum_{j}^{} p_{g j}, {max}_{}^{}_{j}^{} \sum_{g}^{} p_{g j}} \end{matrix}

teljesül.

4. Bizonyítsuk be az ikrekről szóló állítást.

Farkas Gyula, Budapest