Cím:	1996. évi Kürschák József Matematikai Tanulóverseny feladatai és megoldásai
Szerző(k):	Surányi János
Füzet:	1997/február, 66 - 71. oldal	PDF  |  MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd)

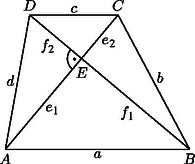
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   1. Igazoljuk, hogy ha egy trapéz átlói merőlegesek, akkor szárainak szorzata legalább akkora, mint a párhuzamos oldalak szorzata.   I. megoldás. Jelöljük az átlók metszéspontját $E$-vel, az $AB$, $BC$, $CD$, $DA$, $AE$, $EC$, $BE$, $ED$ szakaszok hosszát rendre $a$, $b$, $c$, $d$, $e_1$, $e_2$, $f_1$, $f_2$-vel (1. ábra). Ekkor azt kell igazolnunk, hogy $bd\ge ac$. Mivel minden tényező pozitív, azért ez egyenértékű annak igazolásával, hogy $b^2{d}^2\ge a^2{c}^2$. Mindegyik tényező egy-egy derékszögű háromszög átfogója. Ezeket Pitagorasz tétele alapján kifejezve az $\begin{array}{c}{\displaystyle \left(e_2^2+f_1^2\right)\left(e_1^2+f_2^2\right)\ge \left(e_1^2+f_1^2\right)\left(e_2^2+f_2^2\right)}\end{array}$ egyenlőtlenséget kell igazolnunk, vagy átrendezve a következőt: $\begin{array}{c}{\displaystyle \left(e_1^2-e_2^2\right)\left(f_1^2-f_2^2\right)\ge 0.}\end{array}$ Ez viszont igaz, mert az $AEB$ és a $CED$ háromszögek hasonlók, így $\begin{array}{c}{\displaystyle e_1\ge e_2\text{és}{f}_1\ge f_2\text{vagy}{e}_1\le e_2\text{és}{f}_1\le f_2\mathrm{.}}\end{array}$ Egyenlőség akkor áll fenn, ha a két háromszög egybevágó, azaz az átlók felezik egymást, tehát a trapéz paralelogramma, mivel pedig az átlói merőlegesek, így rombusz. Ekkor az oldalak egyenlők, s így a két szorzat valóban egyenlő.   II. megoldás. Ismeretes ‐ és a Pitagorasz-tétel négyszeri alkalmazásával könnyen belátható ‐ hogy egy négyszög átlói akkor és csak akkor merőlegesek, ha a szemközti oldalpárok négyzetének az összege egyenlő. Az előző megoldás jelöléseit használva fennáll tehát a következő egyenlőség: $\begin{array}{c}{\displaystyle b^2+d^2=a^2+c^2\mathrm{.}}\end{array}$ Átrendezve és teljes négyzetté kiegészítve ebből az $\begin{array}{c}{\displaystyle {\left(b+d\right)}^2-{\left(a+c\right)}^2=2\left(db-ac\right)}\end{array}$ (1) egyenlőség adódik. Azt kell tehát megmutatnunk, hogy a bal oldal nemnegatív. Ehhez kiegészítjük az ábrát. Hosszabbítsuk meg a $BA$ oldalt $A$-n túl az $AF=c$ szakasszal, továbbá jelöljük $C$ tükörképét $E$-re $G$-vel (2. ábra). Ekkor $ACDF$ paralelogramma, a $BCDG$ deltoidban pedig $BG=b$ és $GD=c$. Így $AGDF$ szimmetrikus trapéz, tehát $GF=d$. 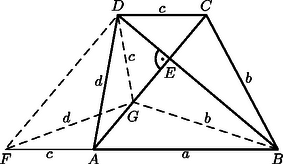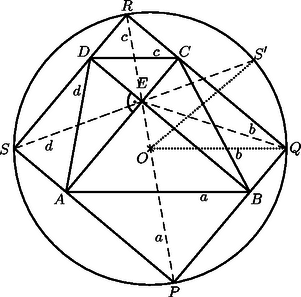A $BGF$ háromszögből a háromszögegyenlőtlenség szerint $\begin{array}{c}{\displaystyle b+d\ge a+c\mathrm{,}}\end{array}$ tehát (1) bal oldala valóban nemnegatív. Egyenlőség akkor áll fenn, ha $G$ $A$-ba esik, vagyis a trapéz átlói felezik egymást, továbbá feltétel szerint merőlegesek, tehát a négyszög rombusz.   III. megoldás. Húzzunk párhuzamosokat a trapéz csúcsain át az átlókkal. Ezek egy $PQRS$ téglalapot határolnak, amit az átlók résztéglalapokra osztanak, így $PE=a$, $QE=b$, $RE=c$, $SE=d$ (3. ábra). Az $ABE$ és $CDE$ háromszögek hasonlók, így az $APBE$ és a $CRDE$ téglalapok is, tehát a $PE$ és az $ER$ átló egy egyenesbe esik, együtt a nagy téglalap átlóját alkotják.   Az ábrán $ac$ eszerint úgy jelenik meg, mint a téglalap köré írt kör átmérője két szeletének szorzata. Messe $SE$ a kört másodszor az $S\text{'}$ pontban. Tudjuk, hogy ekkor $\begin{array}{c}{\displaystyle ac=SE\cdot ES\text{'}=d\cdot ES\text{'}\mathrm{.}}\end{array}$ Azt kell tehát belátnunk, hogy $ES\text{'}\le b$. Feltehetjük, hogy $a\ge c$. Ekkor a kör $O$ középpontja a $PE$ szakaszra esik. A $QOS\text{'}$ háromszög egyenlő szárú. Alapjának a felező merőlegese $O$-n megy keresztül, tehát az $OR$ szakaszra eső $E$ pontra $\begin{array}{c}{\displaystyle ES\text{'}\le EQ=b\mathrm{,}}\end{array}$ és ezt kellett belátnunk. Ismét látható, hogy akkor áll fenn egyenlőség, ha $O$ és $E$ egybeesik, amikor is a trapéz rombusz.   2. Egy konferenciára két országból, $A$-ból és $B$-ből érkezik egy-egy azonos létszámú küldöttség; tagjaik közül néhányan már régebbről ismerték egymást. Bizonyítsuk be, hogy az $A$ országbeli tagok közül kiválasztható néhány (legalább egy) úgy, hogy teljesüljön az alábbi lehetőségek valamelyike: * a)a kiválasztottak között a $B$ országbeli tagok mindegyikének páros számú ismerőse van; * b)a kiválasztottak között a $B$ országbeli tagok mindegyikének páratlan számú ismerőse van.   I. megoldás. Legyen a küldöttségek létszáma $n$. Az $A$ országbeli minden csoporthoz hozzárendelünk egy zérusokból és egyesekből álló $n$-elemű sorozatot; ennek a $j$-edik eleme $0$, ha a $B$-beli küldöttség $j$-edik tagja páros számú embert ismer a csoportból, és 1, ha páratlan számút ismer. Így egyrészt $2^n$ különböző sorozat keletkezhet, másrészt $2^n-1$ különböző csoport választható ki az $A$-beli küldöttségből. Ha mindegyik csoporthoz különböző sorozat tartozik, akkor tehát a $\left(\mathrm{0,}\mathrm{0,}\text{...}\mathrm{,}0\right)$ és az $\left(\mathrm{1,}\mathrm{1,}\text{...}\mathrm{,}1\right)$ legalább egyike előfordul, vagyis az a) és b) lehetőségeknek legalább egyike teljesül. 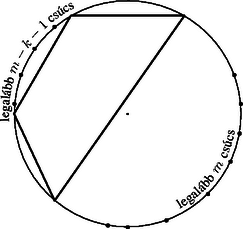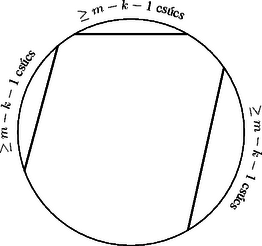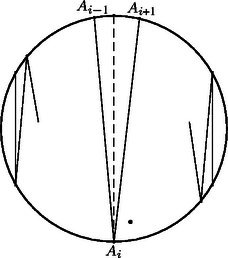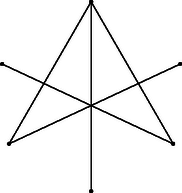Ha van két különböző csoport, amelyikhez ugyanaz a sorozat tartozik, akkor vegyük azokat a küldötteket, akik az elsőben benne vannak, a másodikban nincsenek benne, továbbá azokat, akik az elsőben nincsenek benne, a másodikban benne vannak. Mivel a két csoport különböző, elhagyva azokat (ha vannak), akik mindkét csoporthoz hozzátartoznak, legalább egy $A$-beli küldött marad. Ekkor minden $B$-beli küldött első csoportbeli ismerőseinek a száma ugyanannyival változik, mint a másodikbeli ismerőseinek a száma, a két megmaradt részcsoportbeli küldött ismerőseinek az együttes száma tehát páros. Az így keletkezett csoportra ekkor az a) lehetőség teljesül.   II. megoldás. A küldöttségek létszáma ($n$) szerinti teljes indukcióval bizonyítjuk a feladat állítását. Egytagú küldöttségek esetén az $A$-beli küldöttet vagy ismeri a $B$-beli küldött, vagy nem. Ennek megfelelően a b) vagy az a) lehetőség teljesül. Tegyük most fel, hogy $n$-tagú küldöttségek esetén igaz a bizonyítandó állítás, és tekintsünk két $\left(n+1\right)$-tagú küldöttséget. Az $A$-beli küldöttség tagjait jelöljük $a_i$-vel, a $B$-beli tagjait $b_i$-vel, $i=1$, $2$, $\text{...}$, $n+1$. Hagyjuk egyelőre figyelmen kívül $b_{n+1}$-et. Ha sorra figyelmen kívül hagyjuk $a_1$-et, $a_2$-t, $\text{...}$, $a_{n+1}$-et, akkor a megmaradók közül mindig van legalább egy jó kiválasztás, tehát olyan, amelyikhez vagy az $n$-darab 0-ból álló sorozat, vagy az $n$ darab 1-ből álló sorozat tartozik. Ezek a jó kiválasztások az $\left(n+1\right)$-tagú küldöttségből is kiválasztások. Közülük egyesek állhatnak ugyanazokból az $A$-beli küldöttekből, de nem kaphattuk mindegyik esetben ugyanazt a csoportot, mert mindegyik $A$-beli küldöttet figyelmen kívül hagytuk egyszer. Vegyünk két különböző jó kiválasztást. Ha valamelyikből $b_{n+1}$ is ugyanolyan párosságú embert ismer, mint a küldöttsége többi tagjai, akkor a csoportra teljesül a megfelelő lehetőség az egész $B$-beli küldöttséget véve is tekintetbe. Ha nem ez a helyzet, és mind a két csoporthoz az $n$ darab $c$-ből álló sorozat tartozik, ahol $c$ vagy $0$, vagy $1$, akkor a $b_{n+1}$-hez tartozó szám mind a két csoport esetében $1-c$. Ha a két csoporthoz különböző $n$-elemű sorozatok tartoznak, akkor $b_{n+1}$ az egyik csoportból páratlan számú embert ismer, a másikból páros számút, csak fordított sorrendben, mint a többiek. Vegyük azokat az $A$-beli embereket, akik valamelyik csoportban benne vannak, de nem mind a kettőben. Ekkor minden $B$-beli embernek ugyanannyival változik az első csoportbeliek közti ismerőseinek a száma, mint a második csoportbeliek közöttieké. Így a megmaradottak között az első esetben minden $b_i$-nek összesen páros számú ismerőse van, beleértbe $b_{n+1}$-et is; a második esetben viszont minden $B$-beli küldöttnek, $b_{n+1}$-nek is páratlan számú ismerőse van. Található tehát jó kiválasztás $\left(n+1\right)$-tagú küldöttségek esetében is. Ez a tulajdonság tehát öröklődik, így akárhány tagú küldöttségre fennáll.   3. Jelöljön $n$ és $k$ tetszőleges nemnegatív egész számot. Tegyük fel, hogy egy konvex $n$-szögnek berajzoltuk $2kn+1$ átlóját. Bizonyítsuk be, hogy létezik olyan töröttvonal, amely $2k+1$ berajzolt átlóból áll, és egyetlen ponton sem halad át egynél többször. Mutassuk meg, hogy $kn$ átló berajzolása esetén ez nem feltétlenül igaz.   Megoldás. Olyan töröttvonal létezését bizonyítjuk, amelyik nem záródik. Világos, hogy nem változtat a feladaton, ha azt tesszük fel, hogy legalább $2kn+1$ átló van berajzolva. A feladat állítását $k$ szerinti teljes indukcióval bizonyítjuk. $k=0$ esetén 1 átló van berajzolva, és ez megfelel a feltételnek. Tegyük most fel, hogy adott (elegendő nagy) $n$ esetén az $n$-oldalú sokszögekre $k$-nak valamilyen $j$ értékével igaz az állítás, és egy $n$-szögben $2\left(j+1\right)n+1$ átló van berajzolva. Ekkor az olyan csúcsoknál (ha vannak), amelyekből egy berajzolt átló indul, hagyjuk egyelőre figyelmen kívül ezt az átlót, amelyekből pedig egynél több átló indul, ott a hozzá a két oldalon legközelebbi csúcshoz vezető átlót. Ezzel legfeljebb $2n$ átlót hagyunk el. Ekkor legalább $2jn+1$ berajzolt átló marad meg, tehát kiválasztható közülük egy $2j+1$ átlóból álló töröttvonal. Jelöljük ebben az első és utolsó átlót $A_0{A}_1$, illetve $A_{2j}{A}_{2j+1}$-gyel. A töröttvonal az $A_0{A}_1$, illetőleg az $A_{2j}{A}_{2j+1}$ egyenesek egyik oldalára esik, hiszen nem megy át egy ponton egynél többször, és a sokszög konvex. Miután maradt még a végpontokból induló, behúzott átló, így azokban két-két átlót hagytunk figyelmen kívül. Ekkor azonban hozzácsatolhatjuk mindegyik végponthoz azt az eddig figyelmen kívül hagyott átlót, amelyik a szélső szakasz egyenesének a másik oldalára esik, mint a töröttvonal. Ezzel $2\left(j+1\right)+1$ szakaszból álló töröttvonalat kapunk. A bizonyítandó állítás helyessége tehát öröklődik $2\left(j+1\right)n+1$ átló berajzolása esetére is, így minden $k$-ra igaz. A feladat második állítására térve az általánosság csorbítása nélkül feltehetjük, hogy a sokszög szabályos. A könnyebb tárgyalásmód kedvéért mondjunk egy átlót $h$ hosszúságúnak, ha az egyik oldalára a sokszögnek $h$ oldala esik, a másikra ennyi vagy ennél több. Megjegyezzük, hogy egy $n$ oldalú sokszögbe akkor rajzolható be $nk$ átló, ha páratlan $n$ esetén $n\ge 2k+3$, páros $n$ esetén pedig $n\ge 2k+4$. Belátjuk, hogy az állítás igazolására alkalmas a következő konstrukció: páratlan $n$ esetén minden csúcsból meghúzzuk a $k$ leghosszabb átlót, páros $n$ esetén pedig a $k$ leghosszabb átlót a ,,legesleghosszabb'' (a szemközti csúcsokhoz vezető) kivételével. Így minden csúcs $2k$ átló végpontja, tehát $2kn$ átlóvégpont, azaz $kn$ átló jön létre. Tegyük fel, hogy kiválasztható $r$ szakaszból álló, $A_0{A}_1\text{...}{A}_{r-1}{A}_r$ nyílt töröttvonal, amelyik egy ponton sem megy át egynél többször. Az $A_0{A}_1$ egyenes határolta egyik félsíkba esik az egész töröttvonal, így nem mehet át a töröttvonal az ellenkező oldalra eső félsík belsejében levő sokszögcsúcsokon, és ugyanez mondható az $A_{r-1}{A}_r$ egyenesről is (4. ábra). Ez a két átló nem metszi egymást, így az $A_i$ csúcsok a sokszög kerületének az egyeneseik közti két szakaszán helyezkednek el. Ha $n$ páratlan, $n=2m+1$, akkor a kizárt sokszögcsúcsok száma legalább $2\left(m-k\right)$, a töröttvonalak száma legfeljebb $n-2\left(m-k\right)=2k+1$, és így a töröttvonal $r\le 2k$ szakaszból áll. Ha az oldalszám páros, $n=2m$, akkor a berajzolt leghosszabb átló hossza $m-1$, a legrövidebbé $m-k$. A fenti gondolatmenettel ezért csak $r\le 2k+1$ adódik, így gondosabban szemügyre kell venni a konstrukciót. Ha valamelyik íven van két szomszédos csúcs, akkor az ezeken átmenő egyenesnek a másik oldalán, mint amelyiken a másik ív van, nem lehet csúcsa a töröttvonalnak. Ekkor $\begin{array}{c}{\displaystyle r+1\le n-3\left(m-k-1\right)\mathrm{,}\text{vagyis}r\le 2k+\left(k+2-m\right)\le 2k}\end{array}$ az előrebocsátott megjegyzés szerint. Ha viszont a csúcsok felváltva a két íven vannak (a töröttvonal ,,cikkcakkban'' halad), és pl. az $A_0{A}_1$ egyenesnek a töröttvonalat nem tartalmazó oldalára a sokszög kerületének a felénél nagyobb része, tehát legalább $m$ csúcsa esik, akkor a töröttvonal csúcsainak száma legfeljebb $k+1$, mivel az $A_{r-1}{A}_r$ egyenesnek a töröttvonalat nem tartalmazó oldalán legalább $m-k-1$ csúcs van (5. ábra). Ha a sokszög középpontja a két átló egyenese közt, tehát valamelyik $A_{i-1}{A}_i{A}_{i+1}$ háromszögben van (6. ábra), akkor az $A_i$-vel szemközti sokszögcsúcs nem lehet a töröttvonal csúcsa, így a töröttvonalnak legfeljebb $\begin{array}{c}{\displaystyle 2m-2\left(m-k-1\right)-1=2k+1}\end{array}$ csúcsa lehet, s így legfeljebb $2k$ átlóból állhat.   Megjegyzés. A gondolatmenet pontosabb elemzésével belátható, hogy zárt töröttvonalat is megengedve az eljárás csak hatszög és $k=1$ esetén enged meg $3\left(=2k+1\right)$ hosszúságú töröttvonalat, ekkor azonban a 7. ábrán látható ellenpélda szolgáltat megoldást. Surányi János