Cím:	Az 1996. évi (27.) Nemzetközi Fizikai Diákolimpia feladatainak megoldása
Szerző(k):	Honyek Gyula
Füzet:	1996/november, 495. oldal	PDF  |  MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.     Elméleti verseny       1. feladat. (Ez a példa 5 független kis feladatból áll.) a) öt $1\Omega$-os ellenállást az 1. ábrán látható módon kapcsolunk össze. Az összekötő vezetékek ellenállása elhanyagolható.     1. ábra   Határozd meg az $A$ és $B$ pontok közötti $R$ eredő ellenállást! b) Egy síelő az $A$ pontból nyugalmi helyzetből indulva kanyarodás és fékezés nélkül siklik le a hegyről (2. ábra). A súrlódási együttható $\mu$. A $B$ pontba érve végül megáll, ekkor vízszintes elmozdulása $s$. Mekkora az $A$ és $B$ pontok közötti $h$ magasságkülönbség? (A síelő sebessége olyan kicsi, hogy a lejtő görbületéből származó nyomóerő-változás elhanyagolható. Hanyagold el a légellenállást és a $\mu$ súrlódási együttható sebességfüggését!)     2. ábra   c) Egy ‐ a környezetétől hőszigetelt ‐ fémdarabot légköri nyomás mellett elektromos áram segítségével melegítünk. A fémdarab időben állandó $P$ teljesítménnyel vesz fel energiát, ez a fém hőmérsékletének emelkedését eredményezi. Az abszolút hőmérséklet $\begin{array}{c}{\displaystyle T\left(t\right)=T_0{\left[1+a\left(t-t_0\right)\right]}^{1/4}}\end{array}$ módon függ az időtől ($a$, $t_0$ és $T_0$ állandók). Határozd meg a fém $C_p\left(T\right)$ hőkapacitását (ami a kísérlet hőmérséklet-tartományában hőmérsékletfüggő). d) Egy $T_h$ állandó hőmérsékletű meleg fekete sík felület párhuzamos egy hideg fekete sík felülettel, amelynek $T_l$ hőmérséklete szintén állandó. A síkok között vákuum van. A sugárzásból származó hőáram csökkentése érdekében hővédő pajzsot helyezünk el a meleg és a hideg felületek között, amely két vékony, egymástól hőszigetelt, a sík felületekkel párhuzamos fekete lemezből áll. Egy idő után állandósult állapot jön létre. 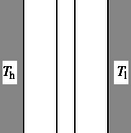    3. ábra   Mekkora $\xi$ tényezővel csökkent az állandósult hőáram a hővédő pajzs jelenlétének következtében? A felületek véges méretéből származó hatásokat hanyagold el! e) Két nagyon hosszú, nem-mágneses anyagból készült, egyenes, egymástól elszigetelt $C_{+}$ és $C_{-}$ vezetőben $I$ áram folyik rendre a pozitív és a negatív $z$ tengely irányában. A vezetők keresztmetszeteit (a 4. ábrán satírozva láthatók) az $x$‐$y$ síkban fekvő $D$ átmérőjű körök határolják, amelyek középpontjainak távolsága $D/2$. A létrejövő keresztmetszetek területe így külön-külön $\left(\frac{1}{12}\pi +\frac{1}{8}\sqrt[]{3}\right)D^2$. Az egyes vezetők keresztmetszetében az áramok egyenletes eloszlásúak. 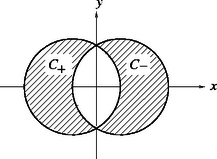    4. ábra   Határozd meg a $B\left(x\mathrm{,}y\right)$ mágneses teret a vezetők közötti térben! 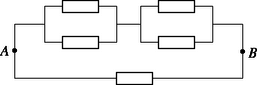  Megoldás. a) A kapcsolás az 5. ábrán látható módon rajzolható át. A párhuzamos és soros kapcsolások ismert szabályai alapján az áramkör eredő ellenállása ,,fejben'' kiszámolható, értéke $\mathrm{0,5}\Omega$.     5. ábra   b) Ha a síelő pályáját elegendően kis szakaszokra osztjuk fel, akkor ezek egyeneseknek tekinthetők. Legyen egy ilyen kis szakasz hossza $\Delta L$, amelyhez $\Delta s$ vízszintes elmozdulás tartozik (6. ábra). Ekkor a súrlódási erő $F_s=\mu mg\Delta s/\Delta L$ alakban adható meg, amivel a súrlódási erő munkája így fejezhető ki: 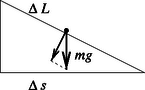$\begin{array}{c}{\displaystyle \Delta W_s=\mu mg\frac{\Delta s}{\Delta L}\cdot \Delta L=\mu mg\Delta s\mathrm{.}}\end{array}$ A súrlódási erők teljes munkáját a $\Delta s$ szakaszok összegzésével kaphatjuk meg: $W_s=\mu mgs$. Az energiamegmaradás értelmében ennek meg kell egyeznie a síelő $mgh$ nagyságú helyzeti energia csökkenésével, amiből $h=\mu s$.     6. ábra   c) Legyen a $dt$ rövid időintervallum alatt bekövetkező hőmérsékletnövekedés $dT$. Eközben a fém $Pdt$ hőt vesz fel. A hőkapacitást (definíciója alapján) így kaphatjuk meg: $\begin{array}{c}{\displaystyle C_p=\frac{Pdt}{dT}=\frac{P}{dT/dt}\mathrm{.}}\end{array}$ A hőmérséklet időbeli változását a megadott függvény deriválásával számíthatjuk ki: $\begin{array}{c}{\displaystyle \frac{dT}{dt}=\frac{T_0}{4}a{\left[1+a\left(t-t_0\right)\right]}^{-3/4}=T_0\frac{a}{4}{\left(\frac{T_0}{T}\right)}^3\mathrm{.}}\end{array}$ így a keresett hőkapacitás: $\begin{array}{c}{\displaystyle C_p=\frac{P}{dT/dt}=\frac{4P}{a{T}_0^4}\cdot T^3\mathrm{.}}\end{array}$   Megjegyzés. Alacsony, de nem különlegesen alacsony hőmérsékleteken a fémek hőkapacitása valóban köbös hőmérsékletfüggést követ.) d) állandósult állapot esetén mindenhol ugyanakkora $J$ hőáramsűrűség (egységnyi felületen időegység alatt átadott hő) alakul ki. A hőáramokat és a hővédő pajzs két lemezének hőmérsékletét a 7. ábra mutatja. 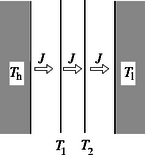    7. ábra   A Stefan‐Boltzmann-törvény felhasználásával a $J$ hőáramsűrűséget háromféleképpen írhatjuk fel: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle J}& {\displaystyle =\sigma \left(T_h^4-T_1^4\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle J}& {\displaystyle =\sigma \left(T_1^4-T_2^4\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle J}& {\displaystyle =\sigma \left(T_2^4-T_l^4\right)\mathrm{.}}\hfill \end{array}}}\end{array}$ Adjuk össze a három egyenletet: $\begin{array}{c}{\displaystyle 3J=\sigma \left(T_h^4-T_l^4\right)=J_0\mathrm{.}}\end{array}$ Mivel $J_0$ éppen a hővédő pajzs nélküli hőáram, a keresett $\xi =J/J_0$ tényező értéke $1/3$. e) A mágneses teret két hengeres vezető terének szuperpozíciójaként határozhatjuk meg. A hengerek részben áthatolnak egymáson, így az ellentétes irányú áramok a közös tartományban kiejtik egymást. A hengeres vezetők $I\text{'}$ árama nagyobb, mint a hold alakú vezetők $I$ árama, az áramok arányát a keresztmetszeti felületek aránya adja meg: 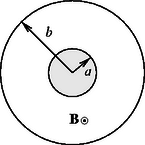$\begin{array}{c}{\displaystyle \frac{I\text{'}}{I}=\frac{\frac{\pi }{4}{D}^2}{\left(\frac{\pi }{12}+\frac{\sqrt[]{3}}{8}\right)D^2}=\frac{6\pi }{2\pi +3\sqrt[]{3}}\mathrm{.}}\end{array}$ Egy $I\text{'}$ áramot hordozó hengeres vezető belsejében, a tengelytől $r$ távolságra a mágneses teret az AmpŠre-féle gerjesztési törvény alapján számíthatjuk ki: $\begin{array}{c}{\displaystyle B_{\phi }=\frac{{\mu }_0}{2\pi r}\frac{I\text{'}\pi r^2}{\frac{\pi }{4}{D}^2}=\frac{2{\mu }_{0}I\text{'}r}{\pi D^2}\mathrm{.}}\end{array}$ A mágneses tér az $r$ sugárra merőleges irányú. Ha a henger tengelye az origóban van, a mágneses tér $x$ és $y$ irányú komponenseit így kaphatjuk meg: $\begin{array}{c}{\displaystyle B_x=-B_{\phi }\frac{y}{r}=-\frac{2{\mu }_{0}I\text{'}y}{\pi D^2};B_y=B_{\phi }\frac{x}{r}=\frac{2{\mu }_{0}I\text{'}x}{\pi D^2}\mathrm{.}}\end{array}$ A szuperponált terek esetén az áramok $\pm I\text{'}$ értékűek, a megfelelő hengerek tengelyei pedig az $x=\pm D/4$ helyeken vannak. Ez nem befolyásolja az $y$ koordináta értékét, tehát a két ellentétes áram miatt a $B_x$ komponens mindenhol eltűnik, továbbá: $\begin{array}{c}{\displaystyle B_y=\frac{2{\mu }_0}{\pi D^2}\left[I\text{'}\left(x+\frac{D}{4}\right)-I\text{'}\left(x-\frac{D}{4}\right)\right]=\frac{{\mu }_{0}I\text{'}}{\pi D}=\frac{6{\mu }_{0}I}{\left(2\pi +3\sqrt[]{3}\right)D}\mathrm{.}}\end{array}$ Tehát a vezetők közötti térben a pozitív $y$ tengely irányába mutató homogén mágneses mező jön létre.   2. feladat. Két azonos tengelyű, hengeres vezető között légritkított tér van. A belső henger sugara $a$, a külső henger belső sugara $b$, amint ezt a 8. ábra mutatja. A külső hengerre, amit nevezzünk anódnak, a belső hengerhez képest pozitív $V$ feszültség kapcsolható. A hengerek tengelyével párhuzamos, homogén, állandó, az ábra síkjából felénk mutató $\text{B}$ mágneses tér is fellép. A vezetőkben létrejövő töltésmegosztás elhanyagolható.     8. ábra   A következőkben $m$ tömegű és $-e$ töltésű elektronok mozgását vizsgáljuk. Az elektronok a belső henger felületéről lépnek ki. a) Először a $V$ feszültséget bekapcsoljuk, de $\text{B}=0$. Egy elhanyagolható sebességű elektron szabadul ki a belső henger felületéről. Határozd meg az elektron $v$ sebességét abban a pillanatban, amikor becsapódik az anódba! A sebességet határozd meg nemrelativisztikus és relativisztikus tárgyalásmóddal is! A továbbiakban már csak a nemrelativisztikus tárgyalást kell használnod! b) Most $V=0$, de a homogén $\text{B}$ mágneses mező jelen van. Egy elektron indul ki ${\text{v}}_0$ kezdősebességgel sugárirányban. Ha a mágneses tér nagyobb egy bizonyos kritikus $B_c$ értéknél, akkor az elektron nem éri el az anódot. Készíts vázlatos rajzot az elektron pályájáról, ha $B$ egy kissé nagyobb, mint $B_c$. Határozd meg $B_c$ értékét! Mostantól kezdve a $V$ feszültség és a $\text{B}$ homogén mágneses mező is jelen van. c) A mágneses mező az elektronnak a hengerek tengelyére vonatkoztatva valamekkora $L$ impulzusmomentumot (perdületet) ad. állíts fel egy egyenletet az impulzusmomentum $dL/dt$ változási sebességére! Mutasd meg: ebből az egyenletből következik, hogy az $L-keB{r}^2$ kifejezés a mozgás során mindvégig állandó, ahol $k$ egy meghatározott szám! Itt $r$ a henger tengelyétől mért távolság. Határozd meg $k$ számértékét! d) Tekintsünk egy, a belső hengerből elhanyagolható sebességgel kilépő elektront, amely nem éri el az anódot, hanem a henger tengelyétől $r_m$ maximális távolságra távolodik. Határozd meg $r_m$ függvényében az elektron $v$ sebességét abban a pontban, ahol a henger tengelyétől mért távolsága maximális! e) Az anódra érkező elektronáramot szeretnénk a mágneses térrel szabályozni. Ha $B$ nagyobb, mint egy kritikus $B_c$ mágneses mező, akkor egy elektron, amely elhanyagolható sebességgel lép ki, nem éri el az anódot. Határozd meg $B_c$ értékét! f) Abban az esetben, ha az elektronok a belső henger fűtésének hatására lépnek ki, általában nullától különböző kezdősebességgel rendelkeznek a belső henger felületén. A kezdősebesség $\text{B}$ vektorral párhuzamos komponense $v_B$, a $\text{B}$ vektorra merőleges komponensei pedig $v_r$ (sugárirányban), illetve $v_{\phi }$ (érintő irányban, azaz a sugárirányra merőlegesen). Határozd meg ebben az esetben az anód eléréséhez szükséges kritikus $B_c$ mágneses mezőt!   Megoldás. a) Az elektron $eV$ potenciális energiája alakul át mozgási energiává. Nemrelativisztikus tárgyalásmódban: $\begin{array}{c}{\displaystyle \frac{1}{2}m{v}^2=eV\mathrm{,}\text{amiből}v=\sqrt[]{\frac{2eV}{m}}\mathrm{.}}\end{array}$ (1) Relativisztikus tárgyalásmódban: $\begin{array}{c}{\displaystyle \frac{m{c}^2}{\sqrt[]{1-v^2/c^2}}-m{c}^2=eV\mathrm{,}\text{innen}v=c\sqrt[]{1-{\left(\frac{m{c}^2}{m{c}^2+eV}\right)}^2}\mathrm{.}}\end{array}$ b) A mágneses Lorentz-erő körpályán mozgatja az elektront: 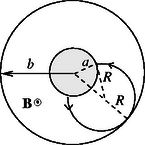$\begin{array}{c}{\displaystyle eB{v}_0=\frac{m{v}_0^2}{R}\mathrm{,}\text{amiből}B=\frac{m{v}_0}{eR}\mathrm{.}}\end{array}$ (2) A kezdősebesség a kör érintőjének irányába mutat. A 9. ábra alapján láthatjuk, hogy a kritikus esetben a következő geometriai feltétel teljesül: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle \sqrt[]{a^2+R^2}=b-R\mathrm{,}\text{amiből}R=\frac{b^2-a^2}{2b}\mathrm{.}}\end{array}}}\end{array}$ Ezt a sugár értéket az (2) egyenletbe helyettesítve kaphatjuk meg a mágneses mező kritikus értékét: $\begin{array}{c}{\displaystyle B_c=\frac{m{v}_0}{eR}=\frac{2bm{v}_0}{\left(b^2-a^2\right)e}\mathrm{.}}\end{array}$     9. ábra   c) A perdület megváltozását valamilyen forgatónyomaték okozza. Beláthatjuk, hogy esetünkben az $\text{F}=\left(-e\right)\text{v}\times \text{B}$ Lorentz-erő sugárra merőleges $F_{\phi }$ komponense fejt csak ki $F_{\phi }r$ forgatónyomatékot. Ilyen irányú erőt viszont csak a sugárirányú $v_r=dr/dt$ sebességösszetevő eredményez. A perdület időbeli megváltozása tehát így írható fel: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{dL}{dt}=eBr\frac{dr}{dt}\mathrm{,}}\\ \hfill {\displaystyle \text{amit a következőképpen alakíthatunk át:}\frac{d}{dt}\left(L-\frac{eB{r}^2}{2}\right)=0.}\end{array}}}\end{array}$ Látható, hogy a $\begin{array}{c}{\displaystyle C=L-\frac{1}{2}eB{r}^2}\end{array}$ (3) mennyiség a mozgás folyamán állandó. A feladatban kérdezett dimenziótlan $k$ szám értéke tehát $k=1/2$. d) A (3) egyenletben szereplő $C$ állandót felírhatjuk akkor, amikor az elektron a belső henger felületéről éppen kilép ($L=0$), illetve amikor $r_m$ maximális távolságra helyezkedik el: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle 0-\frac{1}{2}eB{a}^2=mv{r}_m-\frac{1}{2}eB{r}_m^2\mathrm{,}}\\ \hfill {\displaystyle \text{amiből}\text{(4) }v=\frac{eB\left(r_m^2-a^2\right)}{2m{r}_m}\mathrm{.}}\end{array}}}\end{array}$ e) A kritikus $B_c$ mágneses mező esetén a (4) egyenletben $r_m$ helyére $b$ értékét kell helyettesítenünk, továbbá a sebesség meghatározásakor felhasználhatjuk az (1) egyenlet kifejezését is: $\begin{array}{c}{\displaystyle \frac{e{B}_c\left(b^2-a^2\right)}{2mb}=\sqrt[]{\frac{2eV}{m}}\mathrm{,}}\end{array}$ amiből a keresett $B_c$ könnyen megkapható: $\begin{array}{c}{\displaystyle B_c=\frac{2b}{b^2-a^2}\sqrt[]{\frac{2mV}{e}}\mathrm{.}}\end{array}$ f) A Lorentz-erőnek nincs $B$-vel párhuzamos komponense, ezért a $v_B$ sebesség-összetevő a mozgás során állandó, a kérdésben szereplő kritikus mágneses mezőre $v_B$ nincs hatással. Legyen $v$ az elektron sebességének $B$-re és $r$-re is merőleges komponense a kritikus esetben (amikor éppen eléri az anódot). Az energiamegmaradás szerint: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{1}{2}m\left(v_B^2+v_{\phi }^2+v_r^2\right)+eV=\frac{1}{2}m\left(v_B^2+v^2\right)\mathrm{,}}\\ \hfill {\displaystyle \text{amiből}\text{(5) }v=\sqrt[]{v_r^2+v_{\phi }^2+\frac{2eV}{m}}\mathrm{.}}\end{array}}}\end{array}$ írjuk fel ismét a (3) kifejezésben szereplő $C$ állandót mindkét hengerfelületnél: $\begin{array}{c}{\displaystyle m{v}_{\phi }a-\frac{1}{2}e{B}_c{a}^2=mvb-\frac{1}{2}e{B}_c{b}^2\mathrm{.}}\end{array}$ Végül $v$ helyére írjuk be az (5) kifejezést, amiből a kérdéses kritikus mágneses mező meghatározható: $\begin{array}{c}{\displaystyle B_c=\frac{2m\left(vb-v_{\phi }a\right)}{e\left(b^2-a^2\right)}=\frac{2mb}{e\left(b^2-a^2\right)}\left[\sqrt[]{v_r^2+v_{\phi }^2+\frac{2eV}{m}}-v_{\phi }\frac{a}{b}\right]\mathrm{.}}\end{array}$   3. feladat. Ebben a feladatban a Földön, a nyílt óceánokon kialakuló árapály jelenség néhány alapvető tulajdonságát vizsgáljuk. A feladat megoldásakor a következő egyszerűsítő feltevéseket használjuk: * (i)A Föld és a Hold alkotta rendszert minden mástól elszigeteltnek tekintjük. * (ii)A Hold és a Föld közötti távolságot állandónak vesszük. * (iii)A Földet teljes mértékben óceánnal borítottnak képzeljük. * (iv)A Föld tengely körüli forgásának dinamikai hatásait elhanyagoljuk. * (v)A Föld által kifejtett gravitációs vonzóerő úgy számítható, mintha a teljes tömeg a Föld középpontjában lenne. A következő adatok adottak: A Föld tömege: $M=\mathrm{5,98}\cdot {10}^{24}$ kg; A Hold tömege: $M_m=\mathrm{7,3}\cdot {10}^{22}$ kg; A Föld sugara: $R=\mathrm{6,37}\cdot {10}^6$ m; A Föld középpontja és a Hold középpontja közötti távolság: $L=\mathrm{3,84}\cdot {10}^8$ m; A gravitációs állandó: $G=\mathrm{6,67}\cdot {10}^{-11}\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>3</mn></mrow></msup></mrow></math>k<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>g</mi></mrow><mrow><mo stretchy="false">-</mo><mn>1</mn></mrow></msup></mrow></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>s</mi></mrow><mrow><mo stretchy="false">-</mo><mn>2</mn></mrow></msup></mrow></math>}$. a) A Hold és a Föld $\omega$ szögsebességgel kering a $C$ közös tömegközéppont körül. Milyen messze van $C$ a Föld középpontjától? (Jelöld ezt a távolságot $l$-lel!) Határozd meg $\omega$ számértékét! A továbbiakban használjuk azt a vonatkoztatási rendszert, amely a Hold és a Föld középpontjával együtt a 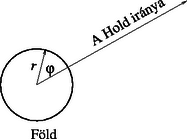$C$ pont körül forog! Ebben a vonatkoztatási rendszerben a Föld folyadékfelszínének alakja állandó. A $P$ síkon, ami átmegy a $C$ ponton és merőleges a forgástengelyre, a Föld folyadékfelszínén lévő tömegpontot az $r$ és $\phi$ polárkoordináták segítségével adhatjuk meg, amint a 10. ábra mutatja. Itt $r$ a Föld középpontjától mért távolság.     10. ábra   A Föld folyadékfelszínének $r\left(\phi \right)=R+h\left(\phi \right)$ alakját fogjuk tanulmányozni a $P$ síkban. b) Tekintsünk egy $m$ tömegű tömegpontot a Föld folyadékfelszínén (a $P$ síkban). Vonatkoztatási rendszerünkben a tömegpontra a centrifugális erő, valamint a Hold és a Föld gravitációs ereje hat. Határozd meg ennek a három erőnek megfelelő potenciális energia kifejezését!   Megjegyzés. Bármely $F\left(r\right)$ centrális erő kifejezhető egy gömbszimmetrikus $V\left(r\right)$ potenciális energia negatív deriváltjaként: $F\left(r\right)=-V\text{'}\left(r\right)$. c) Az adott $M$, $M_m$ stb. mennyiségekkel határozd meg az árapály hatására kialakuló vízfelszínt leíró $h\left(\phi \right)$ függvény közelítő alakját! Mekkora a modell szerint az apály és a dagály szintek közötti különbség méterben? Ha $a\ll 1$, akkor a következő közelítést használhatod: $\begin{array}{c}{\displaystyle \frac{1}{\sqrt[]{1+a^2-2a\text{cos}\theta }}\approx 1+a\text{cos}\theta +\frac{1}{2}{a}^2\left(3\text{cos}{}^2\theta -1\right)\mathrm{.}}\end{array}$ Számításaid során használj egyszerűsítő közelítéseket mindenhol, ahol a közelítés ésszerű!   Megoldás. a) A Föld‐Hold rendszer közös tömegközéppontja a Föld középpontjától $\begin{array}{c}{\displaystyle l=\frac{M_m}{M+M_m}L=\mathrm{4,63}\cdot {10}^6\text{m}}\end{array}$ (1) távolságra van, ami $R$-nél kisebb, tehát a Föld belsejében található. A centripetális erőt a Föld és a Hold közötti gravitációs erő biztosítja: $\begin{array}{c}{\displaystyle Ml{\omega }^2=G\frac{M{M}_m}{L^2}\mathrm{,}}\end{array}$ amibe írjuk be az (1) kifejezést, így megkaphatjuk a kérdéses $\omega$ szögsebességet: $\begin{array}{c}{\displaystyle \omega =\sqrt[]{\frac{G{M}_m}{L^{2}l}}=\sqrt[]{\frac{G\left(M+M_m\right)}{L^3}}=\mathrm{2,67}\cdot {10}^{-6}\frac{\text{1}}{s}\mathrm{.}}\end{array}$ (2) (Ez $2\pi /\omega =\mathrm{27,2}$ napos periódusidőnek felel meg.) b) Az $m$ tömegpont potenciális energiája három tagból áll: $\begin{array}{c}{\displaystyle V=-\frac{1}{2}m{\omega }^2{r}_1^2-G\frac{mM}{r}-G\frac{m{M}_m}{r_m}\mathrm{,}}\end{array}$ ahol az első a forgás miatt fellépő (centrifugális) potenciális energia, a második a Föld, a harmadik pedig a Hold gravitációs vonzásából származó potenciális energia. Az egyes tagokban szereplő $r_1$, $r$ és $r_m$ távolságok jelentését a 11. ábráról olvashatjuk le.     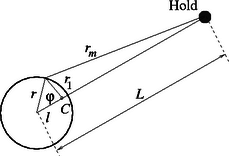11. ábra   A távolságok között a következő összefüggéseket állapíthatjuk meg: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle r_1^2=r^2-2rl\text{cos}\phi +l^2\mathrm{,}}\\ \hfill {\displaystyle r_m=L\sqrt[]{1+{\left(\frac{r}{L}\right)}^2-2\left(\frac{r}{L}\right)\text{cos}\phi }\mathrm{.}}\end{array}}}\end{array}$ c) Mivel az $a=r/L$ hányados nagyon kicsiny, használhatjuk a feladatban megadott közelítést, aminek segítségével a potenciális energia kifejezése így alakítható át: $\begin{array}{c}{\displaystyle \frac{V\left(r\mathrm{,}\phi \right)}{m}=-\frac{1}{2}{\omega }^2{r}^2-\frac{GM}{r}-\frac{G{M}_m{r}^2}{2L^3}\left(3\text{cos}{}^2\phi -1\right)+\text{állandó}\mathrm{.}}\end{array}$ (3) A számításban felhasználtuk, hogy $\begin{array}{c}{\displaystyle m{\omega }^{2}rl\text{cos}\phi -Gm{M}_m\frac{r}{L^2}\text{cos}\phi =\mathrm{0,}}\end{array}$ amiről meggyőződhetünk, ha ${\omega }^2$ helyére a (2) kifejezésben szereplő szögsebességet írjuk. Az egyensúlyban levő folyadékfelszín ekvipotenciális felületet alkot. Helyettesítsük az $r$ sugarat az $r=R+h$ összeggel, ahol az árapályt jellemző $h$ érték sokkal kisebb $R$-nél. Ekkor a következő közelítéseket használhatjuk: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{1}{r}=\frac{1}{R+h}=\frac{1}{R}\frac{1}{1+h/R}\cong \frac{1}{R}\left(1-\frac{h}{R}\right)=\frac{1}{R}-\frac{h}{R^2}\mathrm{,}}\\ \hfill {\displaystyle r^2=R^2+2Rh+h^2\cong R^2+2Rh\mathrm{.}}\end{array}}}\end{array}$ Ezek felhasználásával, továbbá (2) értékének (3)-ba történő behelyettesítésével a potenciál közelítő alakja egy állandótól eltekintve így alakítható át: $\begin{array}{c}{\displaystyle \frac{V\left(r\mathrm{,}\phi \right)}{m}=-\frac{G\left(M+M_m\right)R}{L^3}h+\frac{GM}{R^2}h-\frac{G{M}_m{r}^2}{2L^3}\left(3\text{cos}{}^2\phi -1\right)\mathrm{.}}\end{array}$ A jobb oldal első tagja elhanyagolható a második taghoz képest, mert öt nagyságrenddel kisebb nála, amiről egyszerű átalakítással győződhetünk meg: $\begin{array}{c}{\displaystyle \frac{\left(M+M_m\right)}{M}{\left(\frac{R}{L}\right)}^3\cong {10}^{-5}\mathrm{.}}\end{array}$ Ha a maradék két tag kiegyenlíti egymást, azaz amennyiben $\begin{array}{c}{\displaystyle h=\frac{M_m{r}^2{R}^2}{2M{L}^3}\left(3\text{cos}{}^2\phi -1\right)\mathrm{,}}\end{array}$ akkor $V$ nem függ $\phi$-től, tehát a felület ekvipotenciális. Mivel $r^2$-et bátran $R^2$-tel közelíthetjük, így az árapály magassága $\begin{array}{c}{\displaystyle h=\frac{M_m{R}^4}{2M{L}^3}\left(3\text{cos}{}^2\phi -1\right)\mathrm{.}}\end{array}$ A legnagyobb (dagály) érték ($h_{\underset{}{\overset{}{\text{max}}}}=M_m{R}^4/M{L}^3$) a Hold irányában, illetve az ellenkező oldalon következik be, amikor $\phi =0$ vagy $\pi$, míg a legkisebb (apály) érték $\phi =\pi /2$ esetén $h_{\underset{}{\overset{}{\text{min}}}}=-M_m{R}^4/2M{L}^3$. A maximális dagály és apály közötti különbség így: $\begin{array}{c}{\displaystyle h_{\underset{}{\overset{}{\text{max}}}}-h_{\underset{}{\overset{}{\text{min}}}}=\frac{3M_m{R}^4}{2M{L}^3}=\mathrm{0,54}\text{m}\mathrm{.}}\end{array}$   Megjegyzés. A Csendes-óceán távoli korallzátonyain valóban ekkora különbségeket lehet megfigyelni. A nagy kontinenseknél (különösen meredek partfalak esetén) a feltorlódó dagályhullám akár 15 méteres is lehet.     Kísérleti feladat     A kísérleti feladatsor a fizika több területét átfedte. A mérést egyetlen összetett eszközzel kellett végrehajtani, amelynek leglényegesebb eleme egy fizikai inga volt. Az inga lengésidejét az eszközön található elektronikus óra segítségével lehetett megmérni, amely fényjeleket bocsátott ki, illetve az ingáról visszaverődve észlelt. Az inga segítségével a gravitációs gyorsulás értékét kellett nagy pontossággal meghatározni. A feladat szövegében utalás történt arra, hogy amennyiben ugyanazon fizikai ingát két különböző tengely körül azonos lengésidővel tudjuk mozgatni, akkor g értéke könnyen és pontosan megkapható. Tehát az adott eszközt megfordítható, más szóval reverziós ingaként kellett használni. Az egyik részfeladat értelmében meg kellett vizsgálni az optikai mérőóra geometriáját, az ingán lévő tükröző felület alakját, a kisugárzott és visszavert fénysugarak sugármenetét. A továbbiakban mágneses Hall-cella segítségével egy henger alakú állandó mágnes terét kellett meghatározni a mágnes szimmetriatengelye mentén. Egy elméleti összefüggés ismeretében meg kellett határozni a mágnes remanens mágneses indukciójának értékét. Végezetül vizsgálni kellett, hogy a fizikai ingára szerelt mágnes és egy külső mágnes közötti kölcsönhatás hogyan befolyásolja az inga lengésidejét. Elméleti összefüggések és megadott grafikonok segítségével mérni kellett az ingára rögzített mágnes dipólmomentumát is. Honyek Gyula