Kezdőlap


Cím:	1995. Beszámoló az Eötvös-versenyről
Szerző(k):	Radnai Gyula
Füzet:	1996/április, 236. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1995. október 20-án az országban 15 városban megtartott Eötvös versenyre az alábbi feladatokat tűzte ki a Versenybizottság (elnök: Radnai Gyula, tagok: Károlyházy Frigyes, Gnädig Péter):

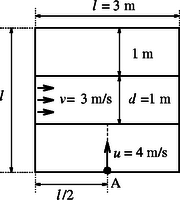
1. feladat. Egy négyzet alakú,

l = 3

m széles kísérletező asztal felszíne sík,

d = 1

m szélességű középső sávját azonban állandó

v = 3

m/s sebességgel mozgó (végtelenített) gumiszalag képezi, amely pontosan illeszkedik az asztallap nyugvó felszínéhez. Az asztal egyik szélének közepére (az 1. ábrán látható

A

pontra) egy kicsi, lapos korongot fektetünk, és megütjük úgy, hogy

u = 4

m/s sebességgel kezdjen csúszni (merőlegesen) a szalag felé. Az asztallap álló része és a korong közötti súrlódás elhanyagolható, a gumiszalag és a korong közötti súrlódási tényező

μ = 0,5.

Hol esik le a korong az asztalról?

Károlyházy Frigyes

Megoldás. Elvileg többféle lehetőség is elképzelhető, a súrlódástól és a sebességektől függően. Kis súrlódás és nagy kezdősebesség esetén a korong szinte átrepül az asztalon, alig változtatja meg a sebességét. Nagy súrlódás és kis kezdősebesség esetén viszont a korong át se jut a futószalagon, hanem ,,leragad'' rajta, és a mozgó szalag szépen elviszi és leejti a korongot az asztal jobb oldalán. Ez utóbbi lehetőség is sugallhatja azt az ötletet, hogy a jelenséget ne az asztalhoz, hanem a futószalaghoz rögzített koordináta-rendszerben vizsgáljuk. Látni fogjuk, hogy ez mennyire leegyszerűsíti a megoldást.
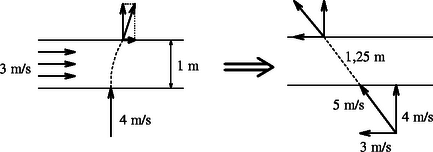
A futószalaghoz rögzített koordináta-rendszerben a korong ferdén csúszik rá az álló szalagra. A súrlódási erő hatására egyenesvonalú, egyenletesen lassuló mozgást végez a szalagon, és ha még marad energiája, le is csúszik róla. Ezt az esetet mutatja a 2. ábra.

az asztalhoz képest (a szalag mozog) a szalaghoz képest (a szalag áll)

A szalagon végigcsúszó korong

1,25 m

utat tesz meg, amíg átér rajta. Kezdősebessége

5 m/s

, lassulása

μ g \approx 5 m/s^{2} .

Végsebessége (a szalag szélén)

\begin{matrix} v_{t} = \sqrt[]{v_{0}^{2} - 2 μ g s} \approx 5 \frac{\sqrt[]{2}}{2} m/s . \end{matrix}

Hol hagyja el a korong a szalagot? Ennek meghatározásáhon számítsuk ki, mennyi ideig volt a korong a szalagon:

\begin{matrix} t_{1} = \frac{2 s}{v_{0} + v_{t}} \approx \frac{1}{2 + \sqrt[]{2}} s . \end{matrix}

Így már kiszámíthatjuk, hogy mennyit mozdult el a szalag, amíg a korong rajta volt:

\begin{matrix} Δ x_{1} = v_{szalag} \cdot t_{1} \approx \frac{3}{2 + \sqrt[]{2}} m . \end{matrix}

az asztalhoz képest a szalaghoz képest

3. ábra

Továbbra is a

g \approx 10 {m/s}^{2}

közelítést alkalmazva a szalagról lecsúszó korong sebességére a futószalag illetve az asztal koordináta-rendszerében a 3. ábrán látható értékeket kapjuk. Az

1 m

széles, súrlódásmentes sávon való átcsúszáshoz szükséges idő:

\begin{matrix} t_{2} = \frac{1 m}{2 \sqrt[]{2} m/s} = \frac{1}{2 \sqrt[]{2}} s . \end{matrix}

Eközben a korong elmozdulása jobbra:

\begin{matrix} Δ x_{2} = (3 - \frac{3}{\sqrt[]{2}}) \frac{1}{2 \sqrt[]{2}} m . \end{matrix}

Így a korong összes elmozdulása jobbra:

\begin{matrix} Δ x = Δ x_{1} - \frac{3}{5} 1,25 m + Δ x_{2} = \frac{3}{2 (2 + \sqrt[]{2})} m \approx 44 cm . \end{matrix}

g = 9,81 {m/s}^{2}

-tel számolunk,

Δ x = 42,6 cm

adódik.
A korong tehát az asztal szemközti oldalának közepétől

42,6 cm

-rel jobbra esik le az asztalról.

2. feladat. Két vékony, koncentrikus, szupravezető gyűrű a síkjukra merőleges, homogén mágneses térben helyezkedik el. A mágneses indukció vektorának nagysága

B_{0}

, iránya az ábrán a papír síkjába befelé mutat. A belső gyűrű sugara sokkal kisebb a külsőénél

(R_{1} ≪ R_{2}) .

Az egyes gyűrűk induktivitása

L_{1}

illetve

L_{2}

, és a kölcsönös indukció sem hanyagolható el.
Mekkora és milyen irányú áramok indukálódnak az egyes gyűrűkben, ha a külső mágneses teret megszüntetjük?

Varga István

Megoldás. A megoldás alapgondolata az, hogy a szupravezető gyűrűkben nem indukálódhat eredő feszültség, mert az végtelen nagy áramot eredményezne. Ez azt jelenti, hogy a külső mágneses tér leépülésével egyidejűleg olyan áramoknak kell indukálódniuk, hogy az áramváltozás miatti önindukciós és külcsönös indukciós feszültségek éppen kioltsák a külső mágneses tér változása miatt indukálódó körfeszültséget. Másképp fogalmazva: a szuravezető gyűrű által körülölelt mágneses fluxus nem változhat meg. Ha megszűnik a külső tér fluxusa, fellép helyette az indukált áramok fluxusa.
Felírhatjuk tehát az alábbi egyenlőségeket:

\begin{matrix} B_{0} R_{1}^{2} π = L_{1} I_{1} + M I_{2} és B_{0} R_{2}^{2} π = L_{2} I_{2} + M I_{1}, \end{matrix}

ahol

M

a két gyűrű közti kölcsönös indukciós együttható. A fenti két egyenletből

I_{1}

és

I_{2}

kifejezhető:

\begin{matrix} I_{1} = \frac{B_{0} (R_{1}^{2} π L_{2} - R_{2}^{2} π M)}{L_{1} L_{2} - M^{2}}, illetve I_{2} = \frac{B_{0} (R_{2}^{2} π L_{1} - R_{1}^{2} π M)}{L_{1} L_{2} - M^{2}} . \end{matrix}

Ezekben a kifejezésekben

B_{0}

R_{1}

R_{2}

L_{1}

és

L_{2}

megadott értékek,

M

-et azonban meg kell még határoznunk.
Hogyan számíthatjuk ki a két gyűrű közötti kölcsönös indukciót? Használjuk ki, hogy

R_{1} ≪ R_{2}

! Feltételezhetjük, hogy az

R_{1}

sugarú, kicsi belső gyűrű belsejében az

I_{2}

áram által átjárt nagy, külső gyűrűből származó mágneses mező jó közelítéssel homogénnek tekinthető. Így a külső gyűrűtől származó fluxus

\begin{matrix} M I_{2} = B \cdot R_{1}^{2} π, \end{matrix}

ahol

B

-t a nagy gyűrűben folyó áram hozza létre a gyűrű közepén, nagysága a Biot‐Savart-törvény alapján:

\begin{matrix} B = μ_{0} \frac{I_{2}}{2 R_{2}} . \end{matrix}

Behelyettesítés után

M

-re a következőt kapjuk:

\begin{matrix} M = μ_{0} \frac{π}{2} R_{1} \frac{R_{1}}{R_{2}} . \end{matrix}

Hasonló megfontolással kaphatunk nagyságrendi becslést az

L_{1}

és

L_{2}

önindukciós együtthatókra is. Egy

R

sugarú körvezetőben folyó áram által létrehozoztt

B_{átlag}

nagyságrendileg közelíthető a középpontban mérhető

B

értékkel. Ennek megfelelően a fluxus

B R^{2} π

, s ezt az árammal osztva az önindukciós együtthatóra

L \approx μ_{0} R π / 2

adódik.

Megjegyzés. Nem tartozik a megoldáshoz, de az érdekesség kedvéért megemlítjük, hogy a körgyűrű induktivitására jó közelítéssel igaz az alábbi formula:

\begin{matrix} L \approx μ_{0} R ln \frac{R}{r}, \end{matrix}

ahol

R

a körgyűrű sugara,

r

pedig a kör keresztmetszetűnek képzelt drót vastagságának a fele. Mivel a logaritmus lassan változó függvény, a gyűrű önindukciós együtthatóját durva közelítésben

μ_{0} R

-rel arányosnak vehetjük.

R_{1} ≪ R_{2}

miatt

M ≪ L_{1} ≪ L_{2}

, ezért az áramokra kapott kifejezéseket tovább egyszerűsíthetjük. A nevezőben

M^{2}

elhanyagolható

L_{1} L_{2}

-höz képest, de elhanyagolható az

I_{2}

számlálójában szereplő második tag is az elsőhöz képest. Így kapjuk:

\begin{matrix} I_{2} = \frac{B_{0} R_{2}^{2} π}{L_{2}}, illetve I_{1} = \frac{B_{0} R_{1}^{2} π}{L_{1}} (1 - μ_{0} \frac{π}{2} \frac{R_{2}}{L_{2}}) . \end{matrix}

Hátra van még az áramok irányának meghatározása.

I_{2}

nyilván a 4. ábrán látható elrendezésben az óramutató járásával megegyező irányban folyik, hogy a papír síkjába befelé mutató indukcióvektort hozzon létre.

I_{1}

iránya nem ennyire magától értetődő, azt a zárójelben álló kifejezés előjele dönti el. Ennek megállapítására ─ Tóth Gábor Zsolt ötlete nyomán ─ használjuk fel, hogy egy körvezetőben folyó áram mágneses tere a kör síkjában fekvő belső pontokat vizsgálva a kör középpontjában a leggyengébb. Felírhatjuk tehát a következő egyenlőtlenséget:

\begin{matrix} Φ_{2} = L_{2} I_{2} > μ_{0} \frac{I_{2}}{2 R_{2}} R_{2}^{2} π = μ_{0} \frac{π}{2} I_{2} R_{2} . \end{matrix}

Ebből következik, hogy

1 > μ_{0} \frac{π}{2} \frac{R_{2}}{L_{2}}

, vagyis az

I_{1}

áram is az óramutató járásával megegyező irányban folyik.

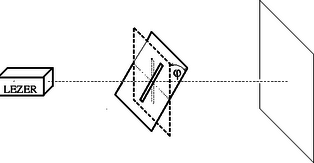
3. feladat. Lézerből jövő, keskeny, vízszintes fénynyalábbal világítjuk meg a függőleges, nagyon keskeny rés középső tartományát.
a) Mit látunk a rés mögötti, a lézersugár irányára merőlegesen elhelyezett ernyőn?
b) Hogyan változik meg az ernyőn látható kép, ha a rést vízszintes középvonala körül

φ

szöggel elforgatjuk? (Legyen például

φ = 45^{\circ}

.)
(A rést tekinthetjük egymáshoz nagyon közeli, egymástól egyenlő távolságra levő piciny lyukak sorozatának. Az ernyő elég távol van a réstől.)

Radnai Gyula

Megoldás. Jelöljük a rés szélességét

a

-val, míg a rés megvilágított, középső tartományának függőleges mérete ─ a lézerből jövő keskeny nyaláb ,,átmérője'' ─ legyen

b

. (Szokásos iskolai kísérleti összeállítás esetén például

b \approx 2

‐3 mm, míg a ,,nagyon keskeny'' rés szélessége biztosan kisebb

0,1 mm

-nél.) Úgy tekinthetjük, hogy egy

b

magasságú és

a

szélességű, téglalap alakú nyílás diffrakciós képe jelenik meg a réstől elég távol elhelyezett ernyőn.
Ebben az esetben vízszintes síkban a

\begin{matrix} sin α_{k} = k \frac{λ}{a} (k = \pm 1, \pm 2, ...) \end{matrix}

egyenlet által meghatározott

α_{k}

irányokban kioltást tapasztalunk. Ha az ernyő

l

távolságra van a réstől

(l ≫ b ≫ a)

, akkor az ernyőn megjelenő kép leginkább egy vízszintes, szaggatott vonalra emlékeztet, ahol a ,,szakaszok'' (függőleges) vastagsága

b

, vízszintes hosszuk pedig mintegy

λ l / a

. (Kivételt képez a középső szakasz, amely kétszeres hosszúságú, mivel

α = 0

irányban is erősítik egymást a hullámok.) Ahogy szűkítjük a rést, a kioltási minimumhelyek egyre távolodnak, és így az ernyőn megfigyelhető szakaszok is egyre hosszabbak lesznek. Előfordulhat, hogy az ernyőn végül már csak egyetlen halvány, összefüggő, vízszintes vonal látható.
Most válaszoljunk a b) kérdésre! Ha a rést elforgatjuk, ,,előre döntjük'' a megadott vízszintes tengely körül, akkor a lézerből jövő fénynyaláb eredeti irányában továbbra is erősítést tapasztalunk. Ez azért van így, mert igaz ugyan, hogy a rés különböző pontjaiba (a lézertől mért távolságok különbözősége miatt) más-más fázissal érkezik a síkhullám, de a résen áthaladva és az eredeti irányban terjedve éppen akkora útkülönbséggel érkeznek az elemi hullámok az ernyőhöz, hogy a teljes fáziskülönbség közöttük nulla. Ennek elképzelését sugallta a feladat szövegében az a zárójelbe tett mondat, hogy ,,a rést tekinthetjük egymáshoz nagyon közeli, egymástól egyenlő távolságra levő piciny lyukak sorozatának''.
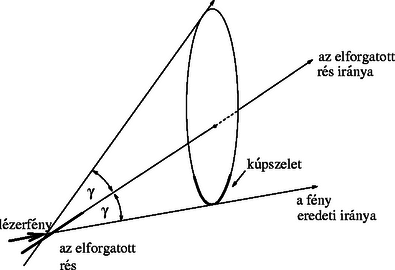
Most már csak azt kell észrevennünk, hogy ha az elemi hullámok a

φ

szögben megdöntött réssel

γ

szöget bezáró irányban

(γ = 90^{\circ} - φ)

erősítik egymást (6. ábra), akkor ez nemcsak az ábra síkjában következik be, hanem a háromdimenziós tér minden olyan irányában, amely a rés irányával ugyancsak

γ

szöget zár be! (Az eredeti, függőlegesen álló rés esetén

γ = 90^{\circ}

, ezért kaptunk ott az ernyőn vízszintes vonalat.)
Általában tehát azt mondhatjuk, hogy az ernyőn megfigyelhető vonal egy kúpnak valamely síkmetszete lesz (7. ábra). A kúp csúcsa a rés közepe, tengelyének iránya a rés iránya, fél nyílásszöge a fenti

γ

, amely az elforgatás szögének pótszöge. A sík az ernyő síkja.
A megfigyelhető vonal egy kúpszelet, ami ─ mint tudjuk ─ ellipszis, parabola vagy hiperbola lehet. Parabolát éppen akkor kapunk, ha az ernyő síkja a kúp valamelyik alkotójával párhuzamos. Esetünkben ez akkor következik be, ha a kúpnak van függőleges alkotója. Vízszintes alkotója az eredeti fénysugár, függőleges tehát csak akkor lehet a másik alkotó, ha a kúp nyílásszöge

90^{\circ}

. Ekkor

γ = 45^{\circ}

φ = 90^{\circ} - γ = 45^{\circ}

, ez az elforgatási szög szerepelt példaként a feladatban.
Ha a rés felső része

45^{\circ}

-ban előre dől az ernyő felé, akkor az ernyőn látható parabola ágai fölfelé állnak. A fény intenzitása a csúcspontban a legnagyobb, a szárakon fokozatosan gyengül.

A verseny eredménye

A beérkezett 262 dolgozat alapos átvizsgálása után a Versenybizottság az alábbi döntést hozta:

Első díjat, s vele járó 6000 Ft pénzjutalmat nyert
Tóth Gábor Zsolt, a budapesti Árpád Gimnázium IV. osztályos tanulója, Vankó Péter tanítványa.

Második díjat nyert és egyenként 4000 Ft pénzjutalomban részesült a következő három versenyző:
Bárász Mihály, a Fazekas Mihály Fővárosi Gyakorló Gimnázium IV. osztályos tanulója, Horváth Gábor tanítványa;
Lengyel Krisztián, az ELTE fizikus hallgatója, aki Cegléden, a Kossuth Lajos Gimnáziumban érettségizett, mint Tűri László tanítványa;
Lovas Rezső, a KLTE Gyakorló Gimnáziumának IV. osztályos tanulója, Dudics Pál, Kirsch Éva és Szegedi Ervin tanítványa.

Harmadik díjat nyert és egyenként 3000 Ft pénzjutalomban részesült a következő négy versenyző:
Fazekas Péter, az ELTE Apáczai Csere János Gyakorló Gimnáziumának IV. osztályos tanulója, Flórik György tanítványa;
Hegyes István, a nyíregyházi Kossuth Lajos Evangélikus Gimnázium IV. osztályos tanulója, Módis Ákos tanítványa;
Szabó János Zoltán, az BME műszaki informatika szakos hallgatója, aki Budapesten, az ELTE Apáczai Csere János Gyakorló Gimnáziumában érettségizett, mint Zsigri Ferenc tanítványa;
Varga Dezső, az ELTE fizikus hallgatója, aki a miskolci Földes Ferenc Gimnáziumban érettségizett, mint id. Szabó Kálmán tanítványa.

Dicséretben részesült a versenyen 9‐10. helyezést elért következő két versenyző: Kurucz Zoltán, a szolnoki Varga Katalin Gimnázium IV. osztályos tanulója, Vincze Gábor tanítványa; Perényi Márton, a Fazekas Mihály Fővárosi Gyakorló Gimnázium IV. osztályos tanulója, Horváth Gábor tanítványa.

Hasonlóképpen dicséretben részesült a versenyen 11-18. helyezést elért alábbi nyolc versenyző:
Agod Attila, a debreceni Tóth Árpád Gimnázium IV. osztályos tanulója, Kovács Miklós tanítványa; Bíró Domokos Botond, a marosvásárhelyi Bolyai Farkas Elméleti Líceum XII. osztályos tanulója, Bíró Tibor tanítványa; Csonka Szabolcs, a budapesti Árpád Gimnázium IV. osztályos tanulója, Vankó Péter tanítványa; Farkas Illés, az ELTE fizikus hallgatója, aki az ELTE Apáczai Csere János Gyakorló Gimnáziumában érettségizett, mint Pákó Gyula tanítványa; a szolnoki Varga Katalin Gimnázium IV. osztályos tanulója, Vincze Gábor tanítványa; Frenkel Péter, a Fazekas Mihály Fővárosi Gyakorló Gimnázium III. osztályos tanulója, Horváth Gábor tanítványa; Lohner Roland, az BME műszaki informatika szakos hallgatója, aki az esztergomi Temesvári Pelbárt Ferences Gimnáziumban érettségizett, mint Halmai László tanítványa; Németh Tibor, az BME műszaki informatika szakos hallgatója, aki a győri Révai Miklós Gimnáziumban érettségizett, mint Somogyi Sándor tanítványa; Vörös Zoltán, a tiszavasvári Váci Mihály Gimnázium IV. osztályos tanulója, Víg Csaba tanítványa.

A díjkiosztásra 1995. november 24-én került sor. Ekkor az érdeklődő diákok és tanárok megtekinthették a feladatokhoz kapcsolódó kísérleteket is, melyeket a Versenybizottság állított össze. Az Eötvös Loránd Fizikai Társulat által biztosított pénzjutalmakat a Nemzeti Tankönyvkiadó nagyjából azonos értékű könyvutalványokkal egészítette ki, ezen kívül a nyertes versenyzők megjelent tanárai a Tankönyvkiadótól és a TypoTeX Kiadótól jutalomkönyveket vehettek át.
A társulati díjakat Németh Judit egyetemi tanár, a Társulat alelnöke adta át biztató szavak kíséretében, míg a Nemzeti Tankönyvkiadó által felajánlott jutalmakat Ábrahám István vezérigazgatótól vehették át a nyertesek és tanáraik. Jelen volt és dedikálta könyvét Staar Gyula, a Természet Világa főszerkesztője is, s a díjkiosztó ünnepségről még aznap sugározta a helyszínen készült tudósítását a Duna Televízió.

Radnai Gyula