Kezdőlap


Cím:	1996. Beszámoló a fizika OKTV-ről
Szerző(k):	Holics László
Füzet:	1996/február, 111 - 120. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A fizika OKTV-t az előző évek gyakorlatához hasonlóan az elmúlt tanévben is három kategóriában és három fordulóban rendezték meg. Az első (iskolai) és a második (megyei) fordulón elméleti problémákat, a harmadik fordulón pedig mérési feladatokat oldottak meg a versenyzők. Az I. kategóriába a szakközépiskolások tartoztak. A II. kategóriában a harmadik gimnazisták (a speciális tantervű osztályok kivételével) és a fizika fakultáción részt nem vevő negyedik gimnazisták, a III. kategóriában pedig a többi gimnazisták versenyezhettek. A végső sorrendet a második és a harmadik fordulóban elért pontszám összege alapján állapította meg a versenybizottság.
Az alábbiakban ismertetjük a verseny II. fordulójának feladatait és azok rövid megoldását, ¹ továbbá vázlatosan utalunk a kísérleti fordulóban szereplő mérési feladatokra is.

Az I. kategória (szakközépiskolások) feladatai

1. feladat. Függőlegesen csapágyazott forgástengelyre erősített vízszintes, elhanyagolható tömegű pálcára négyzet alakú,

100 %

-osan visszaverő tükör van felszerelve az ábra szerint. A tükör tömege

M = 20 g

, a négyzet oldala

a = 10 cm

. A négyzet középpontja a forgástengelytől

r = 20 cm

távolságban van. A tükörre merőlegesen erős napfény süt, amely a tükör minden

{cm}^{2}

-nyi felületére

1 s

alatt

0, 125 J

energiát juttat.
A fénynyomás következtében a berendezés forgásba jön. Mekkora lesz a szögelfordulás

1

perc alatt, ha a rendszer mozgását semmi sem akadályozza, miközben biztosítjuk, hogy a fény a forgás minden fázisában a tükörre merőlegesen haladjon? (A foton energiája és lendülete közötti kapcsolat:

E = I \cdot c

, ahol

c

a fénysebesség.)

(Blészer Jenő)

Megoldás. A tükörre eső fotonok lendületváltozása (elhanyagolható fluktuációtól eltekintve) időben egyenletes, emiatt a tükörre állandó nagyságú erő hat. A fotonok lendületváltozása éppen a kétszerese az általuk szállított lendületnek. (A tükör rendkívül lassan mozog, így a fotonok hullámhossza nem változik meg számottevően a visszaverődés során.)
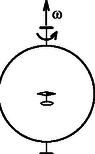
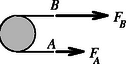
A tükörre ható erő:

\begin{matrix} F = \frac{Δ I}{Δ t} = \frac{A Δ I_{1}}{Δ t} = \frac{2 A E_{1} Δ t}{c Δ t} = \frac{2 A E_{1}}{c} = 8, 33 \cdot 10^{- 8} N . \end{matrix}

(

Δ I

Δ t

idő alatti teljes lendületváltozás,

I_{1}

a lendületsűrűség,

Δ E_{1}

pedig az energiaáramsűrűség, vagyis a másodpercenként területegységenként beérkező energia.) Ennek az erőnek a forgatónyomatéka (átlagos erőkarral számolva):

\begin{matrix} M = 8, 33 \cdot 10^{- 8} N \cdot 0,2 m = 1,67 \cdot 10^{- 8} N m . \end{matrix}

A szerkezet szöggyorsulása a forgómozgás dinamikai alapegyenletéből (

β = M / Θ)

határozható meg. A tükör tehetetlenségi nyomatéka a csapágyazott tengelyre vonatkozóan a Steiner-tétel szerint:

\begin{matrix} Θ = Θ_{TKP} + m r^{2} = \frac{1}{12} m a^{2} + m r^{2} = 8, 17 \cdot 10^{- 4} {kg m}^{2} . \end{matrix}

A szöggyorsulás eszerint

β = 2, 04 \cdot 10^{- 5} s^{- 2}

, az 1 perc alatt bekövetkező szögelfordulás pedig:

φ = β t^{2} / 2 = 0, 0367 rad \approx 2, 1^{\circ} .

(Kérdéses, hogy van-e olyan finom csapágyazás, amivel ez a művelet megvalósítható.)

2. feladat. Egy

0, 1 m

sugarú, kör alakú fémgyűrű a Föld mágneses terében állandó szögsebességgel forog egy olyan függőleges tengely körül, amely átmegy a gyűrű középpontján.
A fémgyűrű középpontjában egy kis mágnestű található, amely függőleges tengely körül szabadon foroghat. Ha a fémgyűrű nem forog, a mágnestű a Föld mágneses tere vízszintes komponensének irányába áll be. Ha a gyűrű

10

fordulatot végez másodpercenként, a mágnestű átlagosan

2

fokkal fordul el ettől az iránytól. Mekkora a gyűrű elektromos ellenállása?

(Honyek Gyula)

Megoldás. A Föld mágneses terének függőleges komponense nem indukál körfeszültséget a gyűrűben, mert ennek a komponensnek megfelelő fluxus állandó (mindvégig nulla). A mágneses indukció vízszintes komponensét jelöljük

\vec{B}

-vel! Ha a gyűrű

ω

szögsebességgel forog, annak mágneses fluxusa:

Φ = r^{2} π B cos ω t .

A gyűrűben indukálódó elektromotoros erő (a harmonikus rezgőmozgás analógiája alapján):

\begin{matrix} E = - \frac{Δ Φ}{Δ t} = r^{2} π B ω sin ω t . \end{matrix}

A gyűrűben folyó áram erőssége:

\begin{matrix} I = \frac{E}{R} = \frac{r^{2} π B ω}{R} sin ω t, \end{matrix}

ahol

R

a gyűrű ellenállása. Jelöljük a gyűrű árama által keltett mágneses tér indukcióját a gyűrű középpontjában

{\vec{B}}_{0}

-lal. Ennek nagysága:

\begin{matrix} B_{0} = μ_{0} \frac{I}{2 r} = μ_{0} \frac{r π B ω}{2 R} sin ω t . \end{matrix}

{\vec{B}}_{0}

mágneses indukció iránya merőleges a gyűrű síkjára és vele együtt forog. Bontsuk fel a

{\vec{B}}_{0}

vektort a Földi mágneses tér vízszintes

\vec{B}

indukciójával párhuzamos és rá merőleges komponensre. A párhuzamos komponens

sin (2 ω t)

-vel arányos, ennek időátlaga tehát nulla. A merőleges komponens:

\begin{matrix} B_{0}^{⊥} = μ_{0} \frac{r π B ω}{2 R} sin^{2} ω t . \end{matrix}

Ennek időátlaga (a szinuszosan változó áram erőssége effektív értékének analógiája alapján):

\begin{matrix} 〈 B_{0}^{⊥} 〉 = μ_{0} \frac{r π B ω}{4 R} . \end{matrix}

Ez az átlagos indukció térítí el a mágnestűt a Föld mágneses terének irányából.
Az iránytű

\vec{B}

és

{\vec{B}}_{0}^{⊥}

eredőjének irányába áll be. Az eltérülés

α

szögére fennáll:

\begin{matrix} tg α = \frac{〈 B_{0}^{⊥} 〉}{B} = μ_{0} \frac{r π ω}{4 R} = μ_{0} \frac{r π^{2} f}{2 R}, \end{matrix}

ahol

f

a gyűrű fordulatszáma. Vegyük észre, hogy a mágnestű elfordulásának szöge nem függ a Föld mágneses tere indukciójának nagyságától, egyedül csak annak van jelentősége, hogy a földi mágneses térnek legyen nullától különböző vízszintes komponense. Továbbá a fenti összefüggés az eltérülés átlagos értékét adja meg. Elképzelhető, hogy a mágnestű kismértékben berezeg új egyensúlyi helyzete körül.

A gyűrű elektromos ellenállásának numerikus értéke:

\begin{matrix} R = μ_{0} \frac{π^{2} r f}{2 \cdot tg α} = 1, 78 \cdot 10^{- 4} Ω \approx 0, 18 m Ω . \end{matrix}

3. feladat. Mekkora vízszintes

F

erővel kell hatnunk az

α

hajlásszögű,

M

tömegű ékre, hogy a rá helyezett

m

tömegű test kétszer annyi idő alatt csússzon az ék mint lejtő tetejéről az aljára, mint nyugvó ék esetén? Az ék és a vízszintes talaj között a súrlódás elhanyagolhatóan kicsi, az ék és a test között a súrlódási tényező

μ

. Az időmérés kezdetén mindkét test nyugalomban van. (

M = 1 kg

m = 1 kg

α = 30^{\circ}

μ = 0, 2

g = 9, 81 m / s^{2}

(Jurisits József)

Megoldás. A lejtőn lecsúszó test függőleges elmozdulása mindkét esetben ugyanakkora, mozgó lejtő esetén azonban kétszer annyi idő kell ehhez. A test függőleges gyorsuláskomponense eszerint nyugvó lejtő esetén négyszer nagyobb, mint mozgó lejtő esetén. Felírva a testek (az ék illetve a rajta csúszó

m

tömegű test) Newton-féle mozgásegyenleteit, a kényszerfeltételt (miszerint az

m

tömegű test mindvégig az ék felületén marad) és a feladat speciális követelményét (a gyorsulások

1 : 4

arányát), olyan egyenletrendszert kapunk, melyből a keresett erő (hosszabb számolás és egyenletrendezés után) az alábbi alakban fejezhető ki:

\begin{matrix} F = g (sin α - μ cos α) [(M + m) \frac{4 - (sin α - μ cos α) sin α}{4 (cos α + μ sin α)} - \frac{M}{4} cos α], \end{matrix}

számértékekkel:

F = 5, 67 N .

A II. és III. kategória (valamennyi gimnazista) feladatai

1. feladat. Egy rögzített henger kerületének felére az 1. ábrán látható módon könnyű, nyújthatatlan fonalat feszítünk ki. Ha a fonál

A

pontját tetszőleges

F_{A}

erővel húzzuk, a fonál súrlódás következtében akkor tapad a hengerre, ha a

B

pontban ható

F_{B}

erő nagyságára a következő egyenlőtlenség teljesül:

(1 / 2) F_{A} \leq F_{B} \leq 2 F_{A} .

A fonál és a henger között a tapadási és csúszási súrlódási együttható megegyezik.
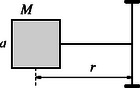
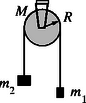
A fentiekben leírt fonállal és a hengerrel a következő kísérletet végezzük el: az

M

tömegű,

R

sugarú tömör hengert vízszintes helyzetű szimmetriatengelyében súrlódásmentesen csapágyazzuk, a hengeren átvetjük a fonalat, amelynek végeire

m_{1}

és

m_{2}

tömegű testeket akasztunk (2. ábra). A hengert rögzítve tarjuk, és a

t = 0

időpillanatban a fonálon függő két testet elengedjük. A henger rögzítését 1 másodperc múlva megszüntetjük. Mekkora lesz a testek sebessége a

t = 4 s

időpillanatban?
Adatok:

M = 9, 9 kg

m_{1} = 0, 9 kg

m_{2} = 2, 2 kg

R = 0, 1 m

g \approx 10 m / s^{2} .

(Honyek Gyula)

Megoldás. Mivel

m_{2} > 2 m_{1}

, a nehezebb test a kötélsúrlódás ellenére felhúzza a könnyebbet. A két test gyorsulása mindvégig azonos. A mozgást három szakaszra lehet bontani: az 1. szakasz addig tart, amíg a hengert rögzítve tartjuk; a 2. szakasz addig, amíg a forgásnak induló henger kerületi sebessége fel nem veszi a fonál sebességét; végül a 3. szakasz alatt a fonál a henger felületéhez tapadva mozog a

t = 4 s

időpillanatig. Vegyük sorra az egyes mozgásszakaszokat!
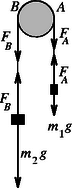
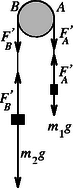
1. szakasz. A bal oldali fonáldarabban

0 \leq t_{1} \leq 1 s

között az erő (a megadott egyenlőtlenségek határhelyzetének megfelelően) kétszer akkora, mint a jobb oldali fonalat feszítő

F

erő. A mozgásegyenletek:

\begin{matrix} \begin{matrix} m_{2} g - 2 F = m_{2} a, \\ F - m_{1} g = m_{1} a . \end{matrix} \end{matrix}

Innen a közös gyorsulás:

\begin{matrix} a = \frac{m_{2} - 2 m_{1}}{m_{2} + 2 m_{1}} g = 1 \frac{m}{s^{2}} . \end{matrix}

A fonálerők ekkor:

F_{A} = F = m_{1} (a + g) = 9, 9 N,

illetve

F_{B} = 2 F_{A} = 19, 8 N .

A testek sebessége

t_{1} = 1 s

-kor

v_{1} = a t_{1} = 1

m/s.
2. szakasz: A testek ugyanúgy mozognak, mint az első szakaszban, azonban az elengedett henger gyorsuló forgást végez. A forgatónyomaték-tétel alapján a henger szöggyorsulása:

\begin{matrix} β = \frac{M_{n y}}{Θ} = \frac{(2 F - F) R}{\frac{1}{2} M R^{2}}, \end{matrix}

ahol

M_{n y}

a hengerre ható erők eredő forgatónyomatéka,

M

a henger tömege. Innen a henger palástjának kerületi gyorsulása:

\begin{matrix} a_{t} = R β = \frac{2 F}{M} = 2 \frac{m}{s^{2}} . \end{matrix}

A henger palástjának pontjai tehát kétszer akkora gyorsulással mozognak, mint a fonálra akasztott testek. A hengerpalást pontjainak sebessége tehát rövid idő múlva megegyezik a fonál sebességével, s ettől kezdve a fonál tapad a hengerhez. Ez az idő a következő egyenletből számítható:

v_{1} + a \cdot t_{2} = 2 a \cdot t_{2},

ahonnan

t_{2} = v_{1} / a = 1 s .

Tehát

t = 2 s

-kor mind a hengerpalást pontjainak, mind a vele érintkező fonálnak ugyanakkora,

v_{2} = 2

m/s lesz a sebessége. Ez a mozgásszakasz tehát az

1 s \leq t \leq 2 s

időintervallumba esik.
3. szakasz: Ennek a hossza 2 s, vagyis a

2 s \leq t \leq 4 s

intervallumba kerül. Ekkor a fonál a henger felületére tapadt, a henger kerületi gyorsulása megegyezik a fonalvégeken függő testek gyorsulásával. A mozgásegyenletek:

\begin{matrix} \begin{matrix} (F'_{B} - F'_{A}) R = \frac{1}{2} M R^{2} β' = \frac{1}{2} M R^{2} \cdot \frac{a'}{R}, \\ m_{2} g - F'_{B} = m_{2} a', \\ F'_{A} - m_{1} g = m_{1} a' . \end{matrix} \end{matrix}

Az egyenletrendszer megoldása:

\begin{matrix} a' = \frac{m_{2} - m_{1}}{m_{2} + m_{1} + \frac{M}{2}} \cdot g = 1,615 \frac{m}{s^{2}} . \end{matrix}

A végsebesség:

v_{3} = v_{2} + a' Δ t = 2 m/s + 1, 615 {m/s}^{2} \cdot 2 s = 5, 23

m/s.
Megjegyezzük, hogy ebben a szakaszban (amikor fonál már nem csúszik a hengeren) az

F_{B}' = 18, 45

N erő kisebb, mint az

F_{A}' = 10, 45

N nagyságú erő kétszerese.

2. feladat. Egy adott mennyiségű nitrogéngáz kezdeti, minimális hőmérséklete

T_{0}

, maximális hőmérséklete

4 T_{0}

. A gázt először állandó térfogaton melegítjük, majd állandó nyomáson tágulni hagyjuk. Ezután állandó térfogaton hűtjük és végül állandó nyomáson összenyomjuk. Ekkor a gáz kiindulási állapotába jut vissza. Legfeljebb mekkora lehet a körfolyamat hatásfoka?

(Szegedi Ervin)

Megoldás. Jelöljük a kezdeti nyomást

p_{0}

-lal és a kezdeti térfogatot

V_{0}

-lal! A folyamat során a gáz által felvett legnagyobb térfogat legyen

x V_{0}

. A maximális

p_{1}

nyomás ekkor a gáztörvényből számítható:

\begin{matrix} \frac{p_{0} V_{0}}{T_{0}} = \frac{p_{1} x V_{0}}{4 T_{0}}, \end{matrix}

ahonnan

\begin{matrix} p_{1} = \frac{4 p_{0}}{x} . \end{matrix}

A folyamat hatásfoka:

\begin{matrix} η = \frac{W_{hasznos}}{Q_{fel}} . \end{matrix}

A gáz által végzett (vagyis a hasznos) munka a körfolyamat diagramja által határolt területtel egyenlő:

\begin{matrix} W_{hasznos} = (\frac{4 p_{0}}{x} - p_{0}) (x V_{0} - V_{0}) = p_{0} V_{0} (\frac{4}{x} - 1) (x - 1) = \frac{p_{0} V_{0}}{x} (4 - x) (x - 1) . \end{matrix}

(Látható, hogy csak az

1 \leq x \leq 4

térfogatarányokkal kell foglalkoznunk.)
A gáz a

(0 \to 1)

és az

(1 \to 2)

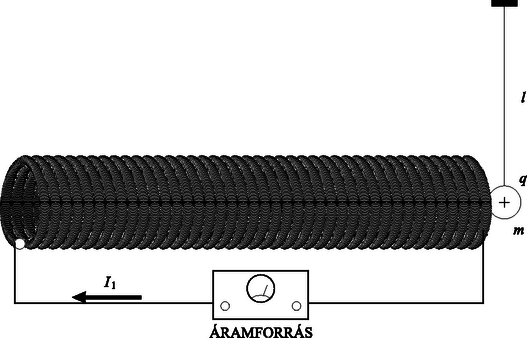
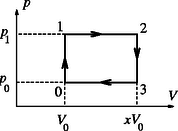
szakaszokon vesz fel hőt. Mivel állandó térfogaton

Q_{0 \to 1} = Δ E_{1}

\begin{matrix} Q_{0 \to 1} = \frac{f}{2} N k Δ T = \frac{f}{2} Δ p V_{0} = \frac{5}{2} (\frac{4 p_{0}}{x} - p_{0}) V_{0} = \frac{5}{2} p_{0} V_{0} \frac{4 - x}{x} . \end{matrix}

Állandó nyomáson:

\begin{matrix} Q_{1 \to 2} = Δ E_{2} + p Δ V = \frac{f}{2} p_{1} Δ V + p_{1} Δ V = \frac{7}{2} p_{1} Δ V = \frac{7}{2} \cdot \frac{4 p_{0}}{x} (x V_{0} - V_{0}) = 14 p_{0} V_{0} \frac{x - 1}{x} . \end{matrix}

Ezzel az összesen felvett hő:

\begin{matrix} Q_{fel} = Q_{0 \to 1} + Q_{0 \to 2} = \frac{5}{2} p_{0} V_{0} \frac{4 - x}{x} + 14 p_{0} V_{0} \frac{x - 1}{x} = \frac{p_{0} V_{0}}{x} (11,5 x - 4) . \end{matrix}

A folyamat hatásfoka tehát az

x

paraméter függvényében:

\begin{matrix} η (x) = \frac{W_{hasznos}}{Q_{fel}} = \frac{(4 - x) (x - 1)}{11,5 x - 4} = \frac{x^{2} - 5 x + 4}{4 - 11,5 x} = \frac{f (x)}{g (x)} . \end{matrix}

Ezt a hatásfok-függvényt az

1 \leq x \leq 4

intervallumon ábrázolva és elemezve (vagy deriválás segítségével) kimutatható, hogy maximuma van az

x = 1, 89

helyen. ² Ezt az értéket visszahelyettesítve a függvénybe a hatásfok maximumára

η_{max} = 0, 106

, tehát

10, 6 %

adódik.

3. feladat.

l_{1} = 30 m

hosszú, hajlékony, tömör supermalloyhuzal-kötegre, amelynek relatív permeabilitása

μ_{rel} = 100 000

, kör keresztmetszete

A_{1} = 4 {cm}^{2}

n_{1} = 3

rétegben szorosan felcsévélünk

d_{1} = 1 mm

átmérőjű rézhuzalt. Az így kapott jobbmenetű tekercset egy

d_{2} = 10 cm

átmérőjű körhengerre szintén jobbmenetűen,

n_{2} = 1

rétegben feltekercselve kapunk egy kb.

175 cm

hosszú kettős tekercset. Ennek a tekercsnek szorosan a végéhez igen vékony,

l = 50 cm

hosszú fonálra függesztett

q = 10^{- 7} C

töltésű,

m = 10 mg

tömegű vékonyfalú alumíniumgömböcskét helyezünk.
A dupla tekercsben az eredetileg az ingával átellenes végén befolyó, állandó

I_{1} = 40 A

erősségű áramot

Δ t = 0, 05 s

alatt

I_{2} = - 40 A

-re változtatjuk. A berendezés vákuumban van.
a) Mi történik a kis elektrosztatikai ingával? Állításunkat indokoljuk!
b) Annak az ismeretnek a birtokában, hogy (elméleti számítások szerint) egy hosszú, vékony egyenes tekercs véglapjánál a mágneses indukció a tekercs közepén mért indukciójának a fele, írjuk le az inga viselkedését!

(Holics László)

Megoldás. Oldjuk meg általánosan (paraméteresen) a feladatot! A

d_{2}

átmérőjű hengerre tulajdonképpen mágneses fluxust ,,csévéltünk fel'', amikor az áramjárta vékony tekercsből egy második tekercset készítettünk. Ha a föltekercselt fluxus az időben változik, az indukciótörvény szerint elektromos mező keletkezik. A geometriai analógia miatt ennek az elektromos mezőnek a szerkezete pontosan olyan, mint egy közönséges szolenoid (egyenes tekercs) árama keltette mágneses mezőé. Nem kell tehát mást tenni, mint az áramot fluxusváltozási
gyorsasággal helyettesíteni, és formálisan úgy számolni, mint amikor a tekercs mágneses terét írtuk le, vagyis a gerjesztési törvény helyett az indukciótörvényt alkalmazni.
Mivel mind az elsődleges, mind a másodlagos tekercs a saját átmérőjéhez viszonyítva igen hosszú, jó közelítéssel használhatók a végtelen hosszú szolenoidra vonatkozó összefüggések. Oldjuk meg lépésenként a feladatot!
1. lépés. Meghatározzuk a vékony tekercs mágneses fluxusát. A felcsévélt (elsődleges) tekercs mágneses fluxusa a tengelye mentén mért indukció és a keresztmetszet területének szorzatával egyenlő, s ez érvényes marad a feltekercselés után is. Az elsődleges tekercs menetszáma annyi, amennyi elfér a

d_{1}

átmérőjű, szorosan csévélt huzalból az

l_{1} = 30 m

hosszú supermalloy-kötegre, szorozva a rétegek számával:

\begin{matrix} N_{1} = n_{1} \frac{l_{1}}{d_{1}} . \end{matrix}

(1)

Ennek a tekercsnek a kezdeti mágneses fluxusa:

\begin{matrix} Φ_{1} = μ_{0} μ_{rel} \frac{I_{1} N_{1}}{l_{1}} \cdot A_{1} = μ_{0} μ_{rel} I_{1} \frac{n_{1} l_{1}}{d_{1} l_{1}} \cdot A_{1} = μ_{0} μ_{rel} I_{1} n_{1} \frac{A_{1}}{d_{1}} . \end{matrix}

(2)

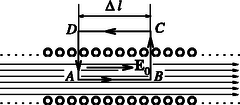
2. lépés. Meghatározzuk az indukált elektromos mező térerősségét. A feltekercselt fluxus keresztmetszetének és a fluxusváltozás keltette elektromos mezőnek az ábrán látható vázlatos képe alapján meghatározhatjuk az indukált elektromos mező térerősségét a nagy tekercs belsejében. Alkalmazzuk az

A B C D A

zárt görbére az indukciótörvényt! Maxwell II. törvénye szerint

\begin{matrix} \sum_{}^{◯} \vec{E} Δ \vec{s} = E_{0} \cdot Δ l + 0 + 0 + 0 = - \frac{Δ Φ}{Δ t} = - \frac{Δ}{Δ t} \sum Φ_{1}, \end{matrix}

(3)

ahol

E_{0}

a duplatekercs közepén mért elektromos térerősség, és

\sum Φ_{1} = N_{2} Φ_{1} .

Itt

N_{2}

Δ l

szakaszra jutó menetek száma, vagyis

N_{2} = n_{2} Δ l / D,

ahol

D

az elsődleges tekercs egy menetének külső átmérője.
Ez közelítőleg a vasmag

D^{*} = 2 \sqrt[]{A_{1} / π}

átmérője, pontosabban a vasmagátmérő és a három rétegű rézhuzaltekercs rétegvastagságának kétszerese, ami egyszerű tekercselésnél

D^{* *} = 2 \sqrt[]{A_{1} / π} + 6 d_{1}

, még pontosabban a legszorosabb tekercselés esetén

D = 2 [\sqrt[]{A_{1} / π} + d_{1} (1 + \sqrt[]{3})]

. Ezzel

\begin{matrix} N_{2} = n_{2} \frac{Δ l}{2 [\sqrt[]{A_{1} / π} + d_{1} (1 + \sqrt[]{3})]} . \end{matrix}

(4)

(2)-t (3)-ba írva és (4)-et is felhasználva megkapjuk a tekercs belsejében az elektromos térerősséget:

\begin{matrix} E_{0} = μ_{0} μ_{rel} \frac{Δ I_{1}}{Δ t} \cdot \frac{n_{1} n_{2}}{2 d_{1}} \cdot \frac{A_{1}}{\sqrt[]{A_{1} / π} + d_{1} (1 + \sqrt[]{3})} . \end{matrix}

A duplatekercs végénél (a szolenoid mágneses terének analógiája alapján) az elektromos térerősség nagysága

E = E_{0} / 2 .

(Figyeljük meg, hogy az

A B = Δ l

szakasz hossza, valamint a duplatekercs teljes

l_{1}

hossza az elektromos térerősség végképletéből kiesett. A feladat szövegében a tekercs körülbelüli hosszának megadása arra utalt, hogy a tekercs igen hosszú az átmérőjéhez képest.) Így tehát a kis ingára a fentebb számolt

E

térerősségű elektromos mező hat egy rövid ideig, mégpedig az irányviszonyok miatt a tekercstől eltaszító irányban!
3. lépés. Az ingára ható elektromos erőtér

Δ t

idő alatt

E q Δ t

erőlökést fejt ki, s emiatt az inga

\begin{matrix} v = \frac{E q Δ t}{m} = \frac{1}{2} \cdot μ_{0} μ_{rel} Δ I \cdot \frac{q}{m} \cdot \frac{n_{1} n_{2}}{2 d_{1}} \frac{A_{1}}{\sqrt[]{A_{1} / π} + d_{1} (1 + \sqrt[]{3})} \end{matrix}

kezdősebességgel kilendül. (Látható, hogy a

Δ t

idő a kezdősebesség képletéből kiesett. Megadására csak azért volt szükség, hogy felmérjük, valóban ,,ballisztikus ingaként'' viselkedik az elektrosztatikai inga, vagyis a rá ható erőlökés ideje sokkal kisebb a lengésidőnél, tehát az elektromos taszító erő nem ,,kíséri végig'' az ingát kitérése során.)
4. lépés. Az inga kitérésének

α

szögét a munkatételből kapjuk:

m g l (1 - cos α) = \frac{1}{2} m v^{2},

ahonnan

\begin{matrix} cos α = 1 - \frac{v^{2}}{2 g l} = 1 - \frac{1}{2 g l} {(\frac{1}{2} μ_{0} μ_{rel} \cdot (Δ I) \cdot \frac{q}{m} \cdot \frac{n_{1} n_{2}}{2 d_{1}} \cdot \frac{A_{1}}{\sqrt[]{A_{1} / π} + d_{1} (1 + \sqrt[]{3})})}^{2} . \end{matrix}

A feladat számadataival numerikusan

cos α = 0, 53

adódik, tehát a kis inga közelítőleg

α = arc cos 0, 53 = 58^{\circ}

-os szöggel lendül ki.

Megjegyzések. 1. Ha a tekercsátmérőt nem a szoros csévélésnek megfelelő ,,hatszögrácsos'' menetelhelyezkedésből, hanem durvább közelítésben, a ,,négyzetrácsban'' elhelyezkedő rézhuzalokkal számoljuk, akkor

α = 56^{\circ}

adódik. Ha még durvábban járunk el és a tekercsátmérő számításánál a rézvezeték rétegvastagságát elhanyagoljuk,

α = 74^{\circ}

-ot kapunk. Látható, hogy ennek a 3 mm-es rétegvastagságnak a

22, 6

mm vasmagátmérő melletti elhanyagolása igen tekintélyes eltérést eredményez.
2. A feladat elvben megoldható, de a kísérlet a valóságban az itt leírt módon több ok miatt sem végezhető el.
─ A megvalósításához többmillió volt feszültséget kellene alkalmazni a rendkívül nagy önindukciós együttható miatt, ami megoldhatatlan szigetelési problémákat okozna.
─ A nagyon nagy relatív permeabilitású anyagoknál viszonylag kicsi gerjesztés hatására formálisan nagyon nagy mágneses fluxus adódik. A valóságban ez nem következik be, mert az anyag sokkal hamarabb ,,telítésbe megy'', a mágnesezettsége nem képes egy bizonyos érték fölé emelkedni.
─ A duplatekercs körülbelüli hosszának megadása erős alábecslés volt, nem fér rá 175 cm-re annyi menet. Ez nem befolyásolja a paraméteres megoldást, mert bármilyen helyes számítási módszer esetén a tekercs hossza kiesik.

A kísérleti forduló feladatai

A verseny harmadik, mérési fordulóját kategóriánként más-más helyszínen rendezték meg. Az I. kategóriába tartozók szakközépiskolások Szegeden, a József Attila Tudományegyetemen versenyeztek. Két feladatot kaptak, melyek kidolgozására 2‐2 óra idejük volt. Az egyik mérésnél egy négypólusú ,,fekete dobozba'' elrejtett ohmos ellenállás, kondenzátor, tekercs és félvezető dióda elhelyezését és jellemző adatait kellett meghatározniuk a rendelkezésre álló csengőreduktor és egy kombinált mérőműszer segítségével. (A feladat szövegéből kiderült, hogy a négy áramköri elem egy-egy vége a fekete doboz kivezetéseihez, a másik végük pedig egy közös ponthoz csatlakozott.) A másik mérési feladatban 2 fénykibocsátó dióda (LED), optikai pad (réssel és ráccsal), valamint tápegység és multiméter segítségével

h / e

-t (a Planck-állandónak és az elemi töltés arányát) határozták meg a versenyzők.
A II. kategóriába tartozók kísérleti fordulóját Debrecenben, a Kossuth Lajos Tudományegyetemen rendezték meg, ugyancsak két mérési feladattal. Az első mérésben egy villanymotor fordulatszámát kellett meghatározniuk a versenyzőknek a motor által felvett áram függvényében. Ehhez különböző eszközök (villogó LED, léggömb, univerzális mérőműszer, üvegfúvóka, tolómérő, Bunsen-állvány, mérőhenger vízzel stb.) álltak rendelkezésre. Vizsgálniuk kellett még a LED fényét forgó tárcsán keresztül, s alkalmas fordulatszámnál megfigyelhető sötét csík megjelenéséből a LED működési sajátságaira következtethettek a versenyzők. A másik mérési feladatban NaNO

_{3}

oldat ismeretlen koncentrációját határozták meg a versenyzők az oldat elektromos vezetőképességének mérése segítségével. Rendelkezésükre állt egy ismert koncentrációjú ,,standard'' oldat, elektrolit-tank, 2 univerzális műszer, időmérő, edények és tartóeszközök. Feladat volt még a KMnO

_{4}

kristály oldódásának és a színes KMnO

_{4}^{-}

ionok vándorlásának megfigyelése, s ebből a KMnO

_{4}^{-}

ionok sugarára kellett becslést adjanak a versenyzők.
A III. kategória mérési versenyét Budapesti Műszaki Egyetemen tartották. A verseny (melyben egy adott cukoroldat ismeretlen koncentrációját kellett meghatározni) két részből állt: egy dolgozat (mérési terv) megírásából és a mérés (többféle módon is megoldható) gyakorlati végrehajtásából. A rendelkezésre álló 4 órányi időt a versenyzők saját belátásuk szerint oszthatták meg a két rész között. Miután a mérési terv 1 példányát beadták, megkapták a rendezők által előre megírt ,,segítséget'', amely további elméleti támpontokak, ötleteket adhatott a tényleges méréshez. A rendelkezésre álló eszközök és anyagok: négyféle ismert és egy ismeretlen koncentrációjú oldat, lombikok, mérleg, Bunsen-állvány, Abbe-féle refraktométer (lámpával és kezelési útmutatóval), U-alakú üvegcső, tölcsér, pipetta, cseppentő, stopperóra, kétkarú emelő, vonalzó, pelenka, gumidugó, filctoll és iratkapcsok.

A fizika I. kategória végeredménye

1. Gál Marcell (Budapest, Trefort Á. Műsz. Szki. és Gimn., IV. o.t.),
tanára: Katona Adrásné;

2. Kovács Krisztián (Békéscsaba, Kemény G. Műsz. Szki., IV. o.t.),
tanárai: Mekis László és Varga István;

3. Füzesi Csaba (Debrecen, Gábor D. Műsz. Középisk., IV. o.t.),
tanára: dr. Kopcsa József;

4. Molnár Zsolt (Paks, Energetikai Szakképzési Int., III. o.t.), tanára: Csajági Sándor; 5. Varga Gábor (Pécs, Széchenyi I. Gimn. és Ipari Szki., IV. o.t.), tanára: Juhászné Bányai Zsuzsa; 6. Gyöpös Balázs (Pécs, Széchenyi I. Gimn. és Ipari Szki., IV. o..t.); 7. Kiss Béla (Vác, Boronkay Gy. Műsz. Szki., III. o.t.); 8. Robotka Tamás (Salgótarján, Stromfeld A. Műsz. Szki., IV. o.t.); 9. Bognár Zsolt (Kaposvár, Eötvös L. Műsz. Szki., III. o.t.); 10. Szabó Bálint (Pécs, Zipernowsky K. Ipari Szki., III. o.t.); 11. Birner Norbert (Jászberény, Liska J. Erősáramú Szki. és Gimn., IV. o.t.); 12. Feldmann Márton (Sopron, Vas- és Villamosipari Szki. és Gimn., IV. o.t.).

A fizika II. kategória eredménye

1. Németh Tibor (Győr, Révai M. Gimn., IV. o.t.),
tanárai: dr. Somogyi Sándor és Székely László;

2. Lovas Rezső (Debrecen, KLTE Gyak. Gimn., III. o.t.),
tanárai: Dudics Pál és dr. Szegedi Ervin;

3. Kurucz Zoltán (Szolnok, Varga K. Gimn., III. o.t.),
tanára: Vincze Gábor;

4. Valkó Benedek (Fazekas M. Főv. Gyak. Gimn., IV. o.t.), tanára: Horváth Gábor; 5. Kovács Baldvin (Fazekas M. Főv. Gyak. Gimn., III. o.t.), tanára: Horváth Gábor; 6. Gröller Ákos (Fazekas M. Főv. Gyak. Gimn., III. o.t.), tanára: Horváth Gábor; 7. Bárász Mihály (Fazekas M. Főv. Gyak. Gimn., III. o.t.), tanára: Horváth Gábor; 8. Juhász Sándor (Fazekas M. Főv. Gyak. Gimn., IV. o.t.), tanára: Horváth Gábor; 9. Horváth Péter (Fazekas M. Főv. Gyak. Gimn., IV. o.t.), tanára: Horváth Gábor; 10. Szegedi Kornél (Szolnok, Varga K. Gimn., IV. o.t.), tanára: Nagy Tibor; 11. Király Csaba (Fazekas M. Főv. Gyak. Gimn., III. o.t.); 12. Gillemot László (Fazekas M. Főv. Gyak. Gimn., IV. o.t.); 13. Wágner Ferenc (Tata, Eötvös J. Gimn., IV. o.t.); 14. Tóth Péter (Miskolc, Földes F. Gimn., III. o.t.); 15. Kanta Szabolcs (Zalaegerszeg, Zrínyi M. Gimn., IV. o.t.); 16. Payrits Szabolcs (Sopron, Széchenyi I. Gimn., III. o.t.); 17. Perényi Márton (Fazekas M. Főv. Gyak. Gimn., III. o.t.); 18. Havasi Ferenc (Szolnok, Varga K. Gimn., III. o.t.); 19. Bokodi Géza (Pécs, Nagy Lajos Gimn., III. o.t.); 20. Hegedűs Márton (Fazekas M. Fő. Gyak. Gimn., III. o.t.); 21. Elek Péter (Budapest, Árpád Gimn., III. o.t.); 22. Hegyi Barnabás (Zalaegerszeg, Zrínyi M. Gimn., III. o.t.); 23. Czirók Dénes (Zalaegerszeg, Zrínyi M. Gimn., III. o.t.); 24. Orosz Róbert (Nyíregyháza, Krúdy Gy. Gimn., IV. o.t.).

A fizika III. kategória eredménye

1. Varga Dezső (Miskolc, Földes F. Gimn., IV. o.t.),
tanára: Szabó Kálmán;

2. Valenta Ferenc (Budapest, Apáczai Csere J. Gimn., IV. o.t.),
tanára: Zsigri Ferenc;

3. Szabó János Zoltán (Budapest, Apáczai Csere J. Gimn., IV. o.t.),
tanára: Zsigri Ferenc;

4. Hartmann Péter (Budapest, Petőfi S. Gimn., IV. o.t.), tanára: Szvetnik Endre; 5. Tóth Csaba (Szombathely, Kanizsai D. Gimn., IV. o.t.), tanára: Sinkó Zoltánné; 6. Juhász Bertalan (Debrecen, KLTE Gyak. Gimn., IV. o.t.), tanára: Dudics Pál; 7. Kovács Gábor (Budapest, Radnóti M. Gimn., IV. o.t.), tanára: Markovits Tibor; 8. Katona Gábor (Debrecen, KLTE Gyak. Gimn., III. o.t.), tanára: Szegediné Nagy Judit; 9. Rácz Péter (Budapest, Petőfi S. Gimn., IV. o.t.), tanára: Szvetnik Endre; 10. Buronyi László (Fazekas M. Főv. Gyak. Gimn., IV. o.t.), tanára: Takács Lajos; 11. Salk Miklós (Pécs, Babits M. Gimn., IV. o.t.); 12. Gilyén Péter (Budapest, Piarista Gimn., IV. o.t.); 13. Borsányi Szabolcs (Budapest, Piarista Gimn., IV. o.t.); 14. Nagy Lajos (Miskolc, Földes F. Gimn., IV. o.t.); 15. Szaszkó Sándor (Jászberény, Lehel Vezér Gimn., IV. o.t.); 16. Radnóczi György (Dunakeszi, Radnóti M. Gimn., IV. o.t.); 17. Steiner Gábor (Budapest, Apáczai Csere J. Gimn., IV. o.t.); 18. Görbe Mihály (Kecskemét, Katona J. Gimn., IV. o.t.); 19. Ehreth Imre (Bonyhád, Petőfi S. Gimn., IV. o.t.); 20. Hussami Péter (Budapest, Radnóti M. Gimn., IV. o.t.).

Holics László

¹Az I. forduló feladatai, valamint feladatok részletes megoldása Holics László: Versenyfeladatok ‐ A fizika OKTV feladatai és megoldásai 1961-1995 című könyvében (TYPOTeX Kiadó, Budapest, 1995) található meg. | A Szerk.

²A maximumhely elemi eszközökkel is meghatározható, ha áttérünk a $z = 11, 5 x - 4$ új változóra, s a vizsgálandó $η (z) = A z + B + C / z$ kifejezésnél alkalmazzuk a számtani és mértani közepekre vonatkozó ismert $A z + C / z \geq 2 \sqrt[]{A C}$ egyenlőtlenséget.