Kezdőlap


Cím:	Ló és lovasa, avagy a párbaállítás módszere II. rész
Szerző(k):	Róka Sándor
Füzet:	1996/április, 193 - 196. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Nézzünk továbbra is olyan feladatokat, amelyeknél az $A$ halmaz elemeinek számát úgy határozzuk meg, hogy $A$ elemeihez hozzárendeljük egy olyan $B$ halmaz elemeit, amelyben könnyebb az elemek megszámlálása (lovak helyett a lovasokat számoljuk meg). A párbaállítást valamilyen kódolási eljárás adja meg. Kódolási módszereket használva különféle tételeket tudunk bizonyítani.

Cayley-tétele és a Prüfer-kód¹

Fának nevezünk egy összefüggő gráfot, ha nem tartalmaz kört. Az ábra két fagráfot ábrázol. A fákra vonatkozó legegyszerűbb tétel a következő:

1. ábra

2. ábra

Tétel. Egy

n

szögpontú fa éleinek száma

n - 1

.
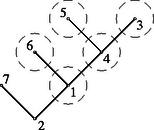
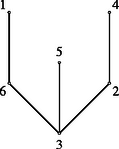
A bizonyítás a következő: Válasszuk ki a fa egy tetszőleges szögpontját, és nevezzük ezt a fa ,,gyökerének". Számozzuk meg a többi pontot az 1, 2,

...

n - 1

számokkal. Számozzunk meg minden élt az él azon végpontjának számával, amely a gyökértől induló és a szóban forgó éllel záródó útnak a végpontja. Ilyen módon minden élt megszámoztunk, és az 1, 2,

...

n - 1

számok mindegyikét pontosan egyszer használtuk fel (minthogy minden pont a gyökérrel egyetlen úttal van összekötve), azaz az élek száma

n - 1

.
Az első nem triviális kérdést a fákról Cayley vetette fel, és ő is oldotta meg: Hány adott pontú különböző fa létezik? A válasz legalább kétféle lehet, attól függően, hogy mikor tekintünk két fát különbözőnek. Mi a számozott szögpontú fák számát fogjuk meghatározni.

Cayley-tétele. Az

n

számozott szögpontú fák száma:

C_{n} = n^{n - 2}

A tétel legszebb bizonyítása Prüfertől 1918-ból származik. A bizonyítás fő gondolata az, hogy minden fához hozzárendel egy olyan

n - 2

számból álló sorozatot, amelynek minden eleme az 1, 2,

...

n

számok valamelyike. Egy ilyen sorozatot a fa Prüfer-kódszavának neveznek. Minthogy az ilyen kódszavak száma

n^{n - 2}

, Cayley formulájának bizonyításához elegendő megmutatni, hogy kölcsönösen egyértelmű megfeleltetés van az

n

-szögpontú számozott fák és a Prüfer-kódszavak között. Ahhoz, hogy ezt belássuk, elég megmutatni, hogyan végezhető el a kódolás és a dekódolás folyamata.
Előbb két egyszerű fogalmat értelmezünk. Egy gráf egy

P

pontját a gráf végpontjának nevezzük, ha fokszáma (a pontból induló élek száma) 1. Az olyan élt, amelynek legalább egyik végpontja a gráfnak végpontja, határoló élnek nevezzük.
A kódolási eljárás:
a) Válasszuk ki a legkisebb számmal megszámozott végpontot (az ábrán levő gráf 3-as számú pontját), távolítsuk el ezt a fából a hozzá vezető határoló éllel együtt, és írjuk le ezen elhagyott él másik végpontjának indexét (a 4-et); ez lesz a kódszó első jele.

44112 Prüfer-kódszó

Prüfer-kódszó: 6233
Dekódolási eljárás: 6233 233 33 3 145 456 256 56 56 36
A megfelelő fa:

b) Ismételjük meg ugyanezt az eljárást a megmaradó fával egészen addig, amíg csak egy 2-szögpontú gráf marad, azután álljunk meg.
A dekódolási eljárás:
Írjuk a kódszó alá növekvő sorrendben az 1, 2,

...

n

számok közül mindazokat, amelyek nem fordulnak elő a kódszóban. Nevezzük ezt a sorozatot antikódnak. Kössük össze a kódszó első jelével számozott pontot az antikód első jegyével számozott ponttal. Hagyjuk el ezeket a jeleket; ha a kódszó elhagyott jegye nem fordul elő többször a kódszó megmaradt részében, írjuk ezt az antikódba a megfelelő helyre. Ismételjük az eljárást az új kódszóval és antikóddal mindaddig, amíg a szó eltűnik. Kössük össze végül azt a két pontot, amelyeknek indexei az utolsó antikódot alkotják.

Az Erdős-Szekeres tétel

Tétel. A különböző valós számokból álló

a_{1}

a_{2}

...

a_{m n + 1}

sorozatnak vagy létezik egy

m

-nél hosszabb csökkenő részsorozata, vagy van egy

n

-nél hosszabb növekvő részsorozata.

Bizonyítás. A sorozat minden eleméhez egy számpárt rendelhetünk:

a_{i} \to (l_{i}^{+}, l_{i}^{-})

, ahol

l_{i}^{+}

jelenti az

a_{i}

-vel kezdődő leghosszabb növekvő részsorozat elemeinek számát,

l_{i}^{-}

a_{i}

-vel kezdődő leghosszabb csökkenő részsorozat elemeinek számát jelenti.
Az így képzett számpárok különbözők. Hiszen, ha

i < j

és

a_{i} < a_{j}

, akkor

l_{i}^{+} > l_{j}^{+}

, ha pedig

a_{i} > a_{j}

, akkor

l_{i}^{-} > l_{j}^{-}

l_{i}^{+}

és

l_{i}^{-}

pozitív egész számot jelöl. Az olyan különböző számpárok száma, melyben

l_{i}^{+} \leq n

l_{i}^{-} \leq m

m \cdot n

. Mivel a sorozat elemeihez rendelt számpárok száma

m \cdot n + 1

, ezért valamelyik

i

-re vagy

l_{i}^{+} > n

vagy

l_{i}^{-} > m

, mely a tétel igazolását jelenti.

A Sperner-lemma

Tétel. Ha egy

n

elemű

H

halmaznak

A_{1}

A_{2}

A_{3}

...

A_{m}

olyan részhalmazai, hogy egyik sem tartalmazza semelyik másik halmazt, akkor

m \leq (\binom{n}{[\frac{n}{2}]})

Megjegyzés. Az

m = (\binom{n}{[\frac{n}{2}]})

érték elérhető, ha vesszük az

n

elemű

H

halmaz összes

[\frac{n}{2}]

elemű részhalmazát.
A tétel (a Sperner-lemma) bizonyítása többféleképp elvégezhető. Lássuk azt, amelynek ötlete az eddigiek közé illik.

Bizonyítás. A

B_{s} \supset B_{s - 1} \supset ... \supset B_{2} \supset B_{1}

sorozatot láncnak nevezzük. A

H

halmaz

n

hosszúságú láncainak száma

n!

. Ha

| A_{i} | = k_{i}

, akkor

A_{i}

részhalmaz

k_{i}! \cdot (n - k_{i})!

n

hosszúságú láncban szerepel, s ha

i \neq j

, akkor

A_{i}

és

A_{j}

nem lehet ugyanabban a láncban, tehát

\begin{matrix} n! \geq \sum_{i = 1}^{m} k_{i}! (n - k_{i})! \geq m \cdot [\frac{n}{2}]! (n - [\frac{n}{2}])! \end{matrix}

azaz

m \leq (\binom{n}{[\frac{n}{2}]})

A diagram-módszer²

n

szám pozitív egészek összegeként való előállításait az

n

szám partícióinak nevezzük. Különféle kérdések, állítások megfogalmazhatók ehhez kapcsolódva.

Tétel. Az

n

szám olyan felosztásainak száma, amelyekben

k

a legnagyobb rész, egyenlő az

n

szám

k

részre való felosztásainak számával.

Bizonyítás. Ha például

n = 7

és

k = 4

, akkor

4 + 1 + 1 + 1

4 + 2 + 1

4 + 3

a 7 azon felosztásai, amelyekben a legnagyobb rész 4. A 7-nek négy részre való felosztásai pedig:

4 + 1 + 1 + 1

3 + 2 + 1 + 1

2 + 2 + 2 + 1

.
A tétel bizonyítását szemléletesebbé tehetjük, ha az

n

tetszőleges felosztásához egy ún. Ferrers-féle diagramot rendelünk. Például a

3 + 2 + 1 + 1

felosztáshoz tartozó diagramot a bal oldai ábra mutatja.

5. ábra

6.ábra

A diagramot átalakítjuk úgy, hogy a sorokból oszlopok, az oszlopokból pedig sorok váljanak. Ez lesz a konjugált diagram. (Egy diagram konjugáltjának konjugáltja az eredeti diagram lesz.) A jobb oldalon látható az előbbi diagram konjugáltja, mely a 7-nek az egyik olyan felosztását (

4 + 2 + 1

) mutatja, amelyben a legnagyobb rész 4.
A diagramok (és konjugált diagramok) segítségével ‐ ahogyan a példa mutatja ‐ párbaállíthatók az

n

szám olyan felosztásai, amelyekben

k

a legnagyobb rész, azokkal a felosztásokkal, amelyekben az

n

számot

k

részre osztjuk fel. Ez a megfeleltetés igazolja a tételt.

Róka Sándor, Nyíregyháza

¹Lásd Rényi Alfréd: Napló az információelméletről (Gondolat Kiadó, Budapest, 1976) c. könyv 164‐187. oldalait. Arthur Cayley (1821‐1895) angol matematikus, Als Heinz Prüfer a Münsteri Egyetem matematikaprofesszora volt, 1934-ben halt meg.

²A diagram-módszer egyéb szép alkalmazásait találjuk Vilenkin: Kombinatorika (Műszaki Könyvkiadó, Budapest, 1987) c. könyvében a 113‐119. oldalakon.