Cím: Ismét egy egyszerű sejtautomatáról, avagy kutyák a Marsról
Szerző(k):  Kós Géza 
Füzet: 1996/március, 138 - 144. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

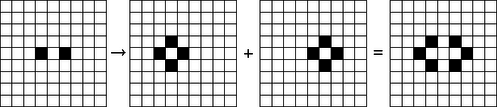
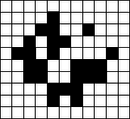
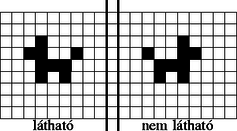
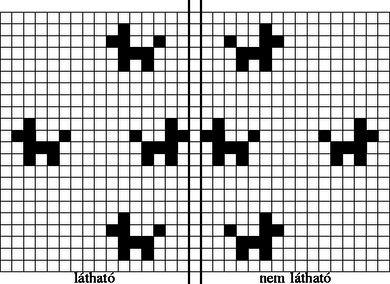
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A játékot, amiről most szó lesz, Eward Fradkin találta ki, s már olvashattunk róla Marx György Szaporodás című írásában (KöMaL 1983/8‐9. szám, 150‐152. oldal). Mivel ez a cikk több mint tíz éve jelent meg, röviden leírjuk a sejtautomata működését.
Képzeljük el, hogy a világ a végtelen négyzethálós papír, melynek mezőin sejtek élnek, egy mezőn legfeljebb csak egy. Elhelyezkedésüket úgy ábrázoljuk, hogy feketére festjük azokat a négyzeteket, amelyek tartalmaznak sejtet. Szabályos időközönként minden sejt négyfelé osztódik, az utódok a négy élben szomszédos mezőre kerülnek. Ha több utód kerül egy mezőre, akkor párosával elpusztítják egymást, amíg legfeljebb csak egy marad. Ez azt jelenti, hogy a következő generációban akkor lesz sejt egy mezőn, ha az előző állapotban a négy szomszéd mező közül páratlan sok (1 vagy 3) tartalmazott sejtet.
Egy sejtből kiindulva, az első generációk az 1. ábra szerint néznek ki.
Az alakzatoknak ezeket az átalakulásait kicsit másképp is elérhetjük.
Tegyük fel, hogy egy mezőben több sejt is lehet, az egy mezőbe kerülő sejtek nem pusztítják el egymást. Azokat a négyzeteket, amelyekben páratlan sok sejt van, feketére festjük, a páros sok sejtet tartalmazó mezőket pedig fehéren hagyjuk. Könnyű végiggondolni, hogy a kapott alakzatok pontosan ugyanúgy néznek ki, mint előbb.
Az átfogalmazás nagyon hasznos: ha ugyanis a kiindulási alakzat több sejtből áll, és kiváncsiak vagyunk arra, hogy mi lesz n generáció múlva, akkor az utódokat kiszámíthatjuk minden egyes kiindulási sejtre, majd a kapott sejtszámokat minden egyes mezőben összeadjuk.
Mi történik az alakzatokkal a sejtszámok összeadásakor? Azok a mezők lesznek feketék, amelyek páratlan sok kiindulási sejt esetében válnak n generáció múlva feketévé. Ezt hívhatjuk az alakzatok egymásra szuperponálásának vagy összeadásának is. A 2. ábrán egy két sejtből álló alakzatra alkalmaztuk ezt az elvet.
Egy másik fontos tulajdonság, hogy egy sejtnek 2n lépés után négy utódja lesz, ezek az eredeti helyhez képest felfelé, lefelé, jobbra, illetve balra helyezkednek el 2n távolságra. Ez például teljes indukcióval bizonyítható be. Ha n=0, akkor az állítás éppen az osztódási előírás. Ha pedig 2n lépés után négy utód van a megadott helyzetben, akkor újabb 2n lépés múlva ezek összesen 16 újabb utódot hoznak létre, amelyek közül csak négy marad meg, pontosan 2n+1 távolságra a négy megfelelő irányban.
Rakjunk össze néhány sejtből egy kisebb alakzatot, pl. kutyát (3. ábra). 2n generáció múlva a kutya minden sejtjének négy utódja keletkezik, amelyek az eredeti sejthez képest 2n távolságra lesznek felfelé, lefelé, jobbra, illetve balra. Ezek az utódok összesen négy kutyává állnak össze. Ha az n kicsi, akkor a négy kutya ,,egymásba lóg'', és a felismerhetetlenségig összezavarják egymást, ,,interferálnak''. Ha viszont az n elég nagy, akkor a négy kutya nem lóg egymásba, hanem jól elkülönül. Ha az eltelt generációk száma nem pontosan kettőhatvány, de van egy elég nagy kettőhatvány osztója, akkor nem négy, hanem több kutyát láthatunk. Egy példa erre a 12. lépés után keletkezett ábra a hátsó borítón.

Kiinduló helyzet

2 lépés után

4 lépés után

3. ábra

 

 
 
Számítógépes program
 
 

A játék számítógépes megvalósítása egy érdekes problémát vet fel. A számítógép ugyanis nem képes végtelen kockás papírt utánozni, hanem csak egy véges téglalapot. Ez azt is jelenti, hogy a képernyő szélén levő sejtek csak háromfelé osztódnak, a négy sarokban pedig csak kétfelé. Kérdés, hogy ez hogyan befolyásolja a végtelen papíron jól kezelhető és rendkívül látványos folyamatot.
Az alábbi program Turbo Pascal programnyelven íródott, és bármilyen IBM XT-kompatibilis számítógépen futtatható:
program SejtAutomata; uses Crt; type Tabla = array[0...40,0...26] of Byte; 
var T: Tabla; procedure AlapAllas; 
var I,J: Integer; 
begin 
TextMode(Co40); 
for I:=0 to 40 do for J:=0 to 26 do T[I,J]:=0; 
T[12,4]:=1; T[11,5]:=1; T[12,5]:=1; T[15,5]:=1; T[12,6]:=1; 
T[13,6]:=1; T[14,6]:=1; T[12,7]:=1; T[14,7]:=1; 
end; procedure Rajzolas; 
var I,J: Integer; 
begin 
for J:=1 to 25 do 
begin 
GotoXY(1,J); 
for I:=1 to 39 do 
if T[I,J]=1 then Write('0') else Write(' '); 
end; 
end; procedure Osztodas; 
var I,J: Integer; T2: Tabla; 
begin 
T2:=T; 
for I:=1 to 39 do for J:=1 to 25 do 
T[I,J] := (T2[I-1,J]+T2[I+1,J]+T2[I,J-1]+T2[I,J+1]) mod 2; 
end; begin 
AlapAllas; 
repeat Rajzolas; Osztodas; until ReadKey<>' '; 
TextMode(Co80); 
end.

A program a szóköz leütésére rajzolja fel a következő generációt, minden más billentyű hatására befejezi működését.
A generációkat tanulmányozva érdekes jelenséget tapasztalunk: a végtelen papíron megszokott kutyákon kívül megjelennek különböző ,,tükörkép'' kutyák is, amelyek bal helyett jobbra néznek, fejjel lefelé állnak vagy éppen fejjel lefelé állnak és jobbra néznek. Mintha a képernyő szélén ,,visszaverődnének'' a kutyák (4. ábra).
A jelenség okát nyilván abban kell keresnünk, hogy a kép szélén levő sejtek osztódási szabálya más. Kevesebb felé osztódnak, a hiányzó utódok utódai hiányoznak a számunkra látható téglalapból. Mindenesetre ez még elég kevés magyarázat. A hiányzó utódok hiányzó utódai hiányzó utódainak hatását elég nehéz nyomon követni, valamilyen más, átfogó módszert kell keresnünk.
 
 
A tükrözési elv
 
 

Hogy megértsük, mi is történik valójában a képernyő szélein, vizsgáljunk először egy egyszerűbb esetet. Legyen a világ egy félsík, határa legyen egy függőleges egyenes. Azt láttuk, hogy az osztódási szabályt nem változtathatjuk meg mesterségesen, mert ‐ egyelőre ‐ nem tudjuk a következményeket leírni. Éppen ezért úgy kell viselkednünk, mintha a világ az egész sík lenne, aminek csak a felét látjuk. Azok a sejtek, amelyek a látható világ szélén helyezkednek el, ugyanúgy négyfelé osztódnak, csak valamilyen, egyelőre nem ismert ok miatt a látható félsíkon kívülre kerülő utódaik azonnal elpusztulnak. Az ok természetesen a világ másik, nem látható felében keresendő. Miért ne lehetnének ott is sejtek, amelyeket ugyan nem látunk, de a hatásukat érzékeljük?
A feladat tehát az, hogy a világ nem látható részébe olyan sejteket helyezzünk el, amelyek utódai garantáltan mindig elpusztítják a láthatóvilágbeli sejteknek a nem látható részbe került utódait. Ezt nagyon egyszerűen megtehetjük. A látható félsík határán kijelölünk egy határsávot, amelyben nem lehet sejt. A határsáv másik oldalán pedig a látható világ tükörképét helyezzük el (5. ábra).
A sejtek elhelyezkedése mindig szimmetrikus lesz a határsávra, ezért a határsáv mezőibe csak párosával, mindkét oldalról egyszerre kerülhetnek sejtek, az ilyen sejtek elpusztítják egymást.
Néhány generáció után a nem látható részben levő kutya sejtjeinek utódai megjelennek a látható félsíkban, például az előbbi helyzet 8 lépés alatt a 6. ábrán látható alakzattá alakul át.
Mindkét kutya a már látottaknak megfelelően négyfelé osztódott, de a nyolc utód kutyának csak a fele látható. A látható félsíkba került az eredeti kutyának három utódja, valamint a tükörkép kutya egyik utódja. A négy látható kutya közül tehát csak három származik az eredeti kutyától, a negyedik, a tükörkép ,,a túlvilágról jött''.
Ha a világ téglalap alakú, akkor bonyolultabb a helyzet. A négy oldal mentén kijelölve egy-egy határsávot, a sík többi részén úgy kell sejteket elhelyeznünk, hogy a kapott alakzat mind a négy határsávra szimmetrikus legyen. Ezt úgy tehetjük meg, hogy a kiindulási téglalappal és a három tükörképével kicsempézzük a síkot a 7. ábra szerint.
A különböző kutyák utódai időnként megjelennek abban a téglalapban is, amelyet látunk. Innen származnak a különféle tükörkép kutyák.
 
 
Feladatok
 
 

 
1. Mi történik akkor, ha a világ nem téglalap, hanem lépcsős, egyenlő szárú derékszögű háromszög?
 
2. Mi a helyzet akkor, ha a sejtek kilencfelé osztódnak, egy utód az eredeti helyen marad, a többi nyolc a csúcsban szomszédos mezőkre kerül?
 
3. Tegyük fel, hogy minden sejt n felé osztódik, az utódok helyére az eredeti helyről a ν1, ν2, ..., νn vektorok mutatnak. Bizonyítsuk be, hogy két lépés után is n utód keletkezik, ezek helyére a 2ν1, 2ν2, ..., 2νn vektorok mutatnak.
 
4. Legyen a világ egy n×k méretű téglalap. Bizonyítsuk be, hogy ha n+1 és k+1 kettőhatvány, akkor bármilyen alakzatból indulunk ki, az előbb-utóbb kipusztul!
 
5. Mi történik akkor, ha a sejtek nem kettesével, hanem hármasával pusztítják el egymást? Hogyan módosul akkor a tükrözési elv?
 
6. Legyen a világ egy n×k méretű téglalap. Bizonyítsuk be, hogy ha bármilyen alakzatból indulunk ki, az előbb-utóbb kipusztul, akkor vagy n+1 és k+1 kettőhatvány, vagy pedig n=k=2.
Kós Géza