Cím: 1995. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldása
Szerző(k):  Surányi János 
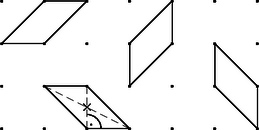
Füzet: 1996/február, 66 - 72. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

 
1. Egy rácstéglalapot, amelyiknek oldalai párhuzamosak a koordinátatengelyekkel, 1/2 területű rácsháromszögekre bontunk. Bizonyítandó, hogy a háromszögek között legalább kétszer annyi derékszögű van, mint a téglalap rövidebb oldalának hossza. (Egy sokszög rácssokszög, ha valamennyi csúcsának mindkét koordinátája egész szám.)
 
Megoldás. A bizonyításhoz előrebocsátunk két észrevételt.
1. Egy rácsháromszög területének kétszerese, például a koordinátageometria területképletéből láthatóan, egész szám. Így az 1/2 területű rácsháromszögek nem tartalmaznak rácspontot a belsejükben, de a csúcsaikon kívül a határukon sem ‐ azt fogjuk mondani, üresek ‐ hiszen különben fel lehetne bontani őket három, illetőleg két rácsháromszögre, s így kétszeres területük 1-nél nagyobb volna.1
2. Az 1/2 területű derékszögű rácsháromszögek befogóinak a hossza 1, és a befogók párhuzamosak a koordinátatengelyekkel, mert egyrészt a szorzatuk a háromszög kétszeres területét adja, másrészt két rácspont távolsága nagyobb mint 1, kivéve, ha egyik koordinátájuk megegyezik, a másik pedig 1-gyel különbözik. Ez azonnal következik a Pitagorasz-tételből.
A feladat állításának bizonyításához először egyes háromszögeket kisebb kerületűvel helyettesítünk, de úgy, hogy fél négyzet (1/2 területű derékszögű rácsháromszög) ne keletkezzék. Ehhez azt vegyük észre, hogy ha két közös oldalú, üres rácsháromszög együtt konvex négyszöget alkot, akkor ez paralelogramma (1. ábra). Valóban, az ilyen négyszög területe 1/2+1/2=1, mindkét átló két ‐ legalább, tehát pontosan 1/2 területű rácsháromszögre bontja, területét felezi, ami azt jelenti, hogy a négyszög paralelogramma. Ha ennek az átlói egyenlők volnának, akkor a négyszög téglalap volna. Így az eredeti két háromszög, mivel területük 1/2, fél négyzet. A fél négyzeteket azonban nem változtatjuk meg.
Nem változtatjuk meg azokat a háromszögeket sem, amelyekből a leírt módon két fél négyzet keletkeznék, vagyis a keletkező paralelogramma rövidebb átlója merőleges az egyik párhuzamos oldalpárra. Az ilyen paralelogramma keletkeztethető egy fél négyzetből úgy, hogy azt az egyik befogó középpontjára tükrözzük (2. ábra). Ekkor a hosszabb átló hossza 5. Nevezzük a továbbiakban az ilyen paralelogrammákat rövidnek.
Ha van a háromszögoldalak közt 5-nél hosszabb, akkor egy maximális hosszúságú oldalra támaszkodó két háromszögre alkalmazhatjuk a leírt eljárást, mert a háromszögekben ezen az oldalon hegyesszög van, mivel a legnagyobb szög a legnagyobb oldallal van szemben. Így a két háromszög együtt konvex négyszöget alkot. Mivel az előforduló legnagyobb rácstávolságból indultunk ki, és a két átló nem egyenlő hosszú, így a másik átló meghúzásával kisebb kerületű háromszögeket kapunk.
Az eljárás véges sok lépésben befejeződik, mert az oldalhosszak négyzete pozitív egész szám, és nem nagyobb a téglalap átlójánál, továbbá mindegyik csak véges sokszor léphet fel. Elég tehát a feladat állítását olyan téglalapokra belátni, amelyek fél négyzetekre és rövid paralelogrammákra vannak felbontva.
Vegyük a téglalap egyik oldalának két szomszédos rácspont közti szakaszát és a felbontásnak azt a sokszögét, amelyiknek ez az egyik oldala. Ha ez háromszög, akkor megállunk, ha rövid paralelogramma, akkor ennek a tengellyel párhuzamos másik oldalára támaszkodó sokszöget vesszük. Az eljárást addig folytatjuk, amig háromszöghöz vagy a téglalapnak a kiindulási oldalával szemközti oldalához nem érünk. Az első esetben a háromszög egyik befogója a téglalap kiindulási oldalával párhuzamos, így a háromszögnek nem lehet közös oldala a téglalap párhuzamos oldalával.
A második esetben a téglalapnak a kiindulási oldallal szomszédos oldalától indulva ki egy egységnyi szakaszból ugyanez az eset csak úgy léphetne fel, ha a két sokszögsorozatnak volna közös rövid paralelogrammája. Ez azonban nem lehetséges, mert az egyik és a másik sorozat rövid paralelogrammáinak a koordinátatengellyel párhuzamos oldala egymásra merőleges (3. ábra).
A leírt eljárás tehát minden esetben legalább kétszer annyi derékszögű üres rácsháromszöget szolgáltat, mint a téglalap valamelyik oldalának a hossza. Ezzel a feladat állítását bebizonyítottuk.
 
2. Adott egy n változós polinom. Tudjuk, hogy ha mindegyik változója helyébe vagy +1-et, vagy -1-et helyettesítünk, értéke pozitív lesz, amennyiben a -1-ek száma páros, és negatív, ha a -1-ek száma páratlan. Igazoljuk, hogy a polinom legalább n-edfokú. (Azaz van olyan tagja, amelyikben a változók kitevőinek az összege legalább n.)
 

Előrebocsátunk egy megjegyzést. Elég olyan polinomokra szorítkozni, amelyekben minden változó legfeljebb első hatványon szerepel. Ha ugyanis minden páros hatványon szereplő változót 1-gyel, a páratlan hatványon szereplőket pedig a változó első hatványával helyettesítjük, ezzel a polinom foka nem növekszik, a feladatban megadott tulajdonsága pedig nyilvánvalóan megmarad, és ezen az sem változtat, ha a módosítás után összevonható tagokat összevonjuk. Ha pedig a módosított polinom legalább n-edfokú, akkor az eredeti is. A továbbiakban polinomon mindig a mondott módon egyszerűsített polinomot értünk2.
 
I. megoldás. Az állítást teljes indukcióval bizonyítjuk. Egy egyváltozós polinom ax+b alakú. Feltétel szerint
a+b>0,-a+b<0,azaza-b>0,
tehát
2a>0,a>0.
A polinom tehát elsőfokú. (Az eredeti polinom legalább elsőfokú.)
Tegyük fel, hogy a legfeljebb m változós polinomokra igaz a feladat állítása. Egy m+1 változós polinom
f1(x1,...,xm)+xm+1f2(x1,...,xm)
alakban írható, ahol f1 és f2 legfeljebb m-változós polinom. Legyen c1, ..., cm egy +1-ekből és -1-ekből álló sorozat. Ha a ci-k közt páros számú -1 van, akkor xm+1-nek egyszer +1, egyszer -1 értéket adva, a feltétel szerint
f1(c1,...,cm)+f2(c1,...,cm)>0f1(c1,...,cm)-f2(c1,...,cm)<0.
Az utóbbit így írhatjuk:
-f1(c1,...,cm)+f2(c1,...,cm)>0és így2f2(c1,...,cm)>0;
ha pedig a ci-k között a -1-ek száma páratlan, akkor
f1(c1,...,cm)+f2(c1,...,cm)<0,f1(c1,...,cm)-f2(c1,...,cm)>0,
tehát
-f1(c1,...,cm)+f2(c1,...,cm)<0és így2f2(c1,...,cm)<0.
Azt kaptuk, hogy f2-nek is megvan a tételben megfogalmazott tulajdonsága, s így az indukciós feltétel szerint legalább m-edfokú, az eredeti polinom legalább (m+1)-edfokú. Ezzel beláttuk, hogy a tétel állítása minden n-re igaz.
 
II. megoldás. Indirekt úton bizonyítjuk a feladat állítását. Az, hogy egy polinom n-nél alacsonyabb fokú, azt jelenti, hogy nincs benne mindegyik változót tartalmazó tag. Tegyük fel, hogy egy ilyen polinomra teljesülnének a feladat feltételei. Képezzük az összes +1-ekből és -1-ekből álló sorozatokon vett értékeit a polinomnak, és a pozitív értékek U összegéből vonjuk le a negatív értékek V összegét. Nyilvánvalóan U-V>0. Nézzük meg, hogy egy axi1xi2...xij tag együtthatója (j<n) hányszor szerepel U-ban és hányszor V-ben. A +1-ekből és -1-ekből álló c1, c2, ..., cn sorozatokban, rögzítve ci1, ci2, ..., cij értékét, ha
ci1ci2...cij=1,
akkor a annyiszor szerepel U-ban, ahányféleképpen a többi c-k közt páros számú -1 fordulhat elő. Ez a szám
r=(n-j0)+(n-j2)+(n-j4)+...,
ahol az összeg addig tart, amíg az alsó páros szám nem nagyobb (n-j)-nél; V-ben pedig annyiszor, ahányféleképpen a többi c-k közül páratlan számút lehet kiválasztani. Ez a szám pedig
s=(n-j1)+(n-j3)+(n-j5)+....
A kiszemelt tag adaléka az U-V különbséghez tehát a binomiális tétel szerint
a(r-s)=a{(n-j0)-(n-j1)+(n-j2)-(n-j3)+...}=a(1-1)n-j=0.

Ha viszont
ci1ci2...cij=-1,
akkor -a szerepel U-ban s-szer, V-ben pedig r-szer, így ekkor is 0 a tag adaléka az U-V különbséghez. Mivel ez az indirekt feltevés szerint a polinom minden tagjára teljesülne, így ellentmondásra jutottunk azzal, hogy ez a különbség pozitív. A polinomban tehát szerepelnie kell az x1x2...xn tagnak nemnulla együtthatóval. Ezzel a feladat állítását igazoltuk.
 
3. Az A, B, C, D pontok közül semelyik három nincs egy egyenesen. Az AB és CD egyenesek E-ben, a BC és DA egyenesek F-ben metszik egymást. Bizonyítsuk be, hogy az AC, BD és EF átmérőjű körök vagy egy ponton mennek át, vagy közülük semelyik kettőnek nincs közös pontja.
 
Megoldás. A pontokat A-ból hozzájuk mutató helyvektoraikkal jellemezzük. AB→=b, AD→=d. Ezek nem párhuzamosak, tehát a sík vektorai felírhatók egyértelműen ezek számszorosainak összegeként. Így
AC→=c=βb+δd
alkalmas β, δ számokkal.
Mivel E az AB és a CD egyenesen van, F az AD és a BC egyenesen, így
e=AE→=εb=λd+(1-λ)c=(1-λ)βb+((1-λ)δ+λ)d,f=AF→=φd=μb+(1-μ)c=((1-μ)β+μ)b+(1-μ)δd.
Itt λ és μ nem lehet sem 0 sem 1, mert E különbözik C-től és D-től, F pedig B-től és C-től, különben A, C és D, illetőleg A, B és C egy egyenesen volna. Az előállítások egyértelműségéből következik, hogy
ε=(1-λ)β,δ=λλ-1,φ=(1-μ)δ,β=μμ-1,
amiből
ε=(1-λ)μμ-1,φ=λ(1-μ)λ-1.
Ezeket felhasználva
c=μμ-1b+λλ-1d,e=(1-λ)μμ-1b,f=λ(1-μ)λ-1d.(1)

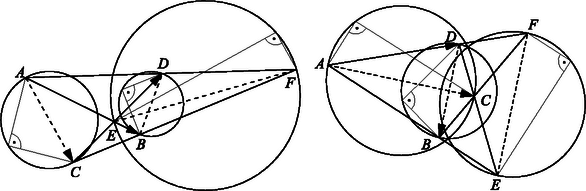
Egy p helyvektorú P pont akkor van az egyes körökön, ha a belőle a megfelelő átmérő végpontjaihoz mutató vektorok merőlegesek, azaz 0 a skaláris szorzatuk3. A feladatban szereplő körök ezért így jellemezhető
p(p-c)=p2-μμ-1pb-λλ-1pd=0,(p-b)(p-d)=p2-pb-pd+bd=0,(p-e)(p-f)=p2-(1-λ)μμ-1pb-λ(1-μ)λ-1pd+λμbd=0.

Jelöljük a bal oldalakat KAC, KBD, KEF-fel. A feladatot megoldottuk, ha sikerül olyan 0-tól különböző α, γ, η számokat találnunk, amelyekre azonosan teljesül, hogy
αKAC+γKBD+ηKEF=0,(2)
mert ekkor, ha egy P pontra valamelyik két kifejezés 0, akkor a harmadik is, tehát ha P valamelyik két körön rajta van, akkor a harmadikon is.
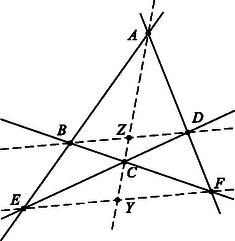
KAC-ben nem szerepel bd-s tag, így bármi is az α, a második kifejezés λμ-szöröséhez a harmadik -1-szeresét adva az összegben ilyen tag nem fog szerepelni. Az összeghez az első kifejezés (1-λμ)-szörösét adva p2 sem fog szerepelni az összegben. Tehát az α=1-λμ, γ=λμ, η=-1 választással a p2-es és a bd-s tagok kiesnek, továbbá a -bp és a -dp együtthatója (2) bal oldalán
(1-λμ)μμ-1+λμ-(1-λ)μμ-1=μμ-1(1-λμ+λ(μ-1)-1+λ)=0;
illetőleg
(1-λμ)λλ-1+λμ-(1-μ)λλ-1=λλ-1(1-λμ+μ(λ-1)-1+μ)=0.

KAC szorzója, α=0 lehetne, ha λμ=1 volna, de ez sem lehetséges. Ha ugyanis ez állna fenn, akkor c (1)-beli előállításában a második törtet λ-val egyszerűsítve azt kapnánk, hogy
c=μμ-1b+11-μdvagyd=μb+(1-μ)c).
Ez azt jelentené, hogy D egybeesnék E-vel, és így egy egyenesen lenne B-vel és C-vel a feladat feltételével ellentétben. Ezzel a feladat állítást bebizonyítottuk.
 
Megjegyzések. 1. A feladatot vektorszámítással megoldó versenyzők többnyire azt számolták ki, hogy ha egy P pontra két egyenlet teljesül, akkor a harmadik is. Ekkor vagy három esetet kell külön-külön végigszámolni, vagy az igényel külön magyarázatot, hogy miért szimmetrikus a három kör szerepe.
2. A feladat megoldható projektív geometriai ismeretek alapján is4. Egy ilyen megoldásnak csak röviden vázoljuk a menetét. Ha R, S, T, U egy egyenes négy különböző pontja, akkor az RT/TS arányt, ezt pozitívnak tekintve, ha a két szakasz egyirányú, negatívnak, ha ellentétes irányú, a három pont osztóviszonyának nevezzük, és (RST)-vel jelöljük. Az (RST)/(RSU) arány a négy pont kettősviszonya, jelölése (RSTU). Ez akkor negatív, ha az R, S és a T, U pontpár elválasztja egymást.
Ha a kettősviszony értéke -1, akkor azt mondjuk, hogy a négy pont harmonikus pontnégyes, illetőleg R, S és T, U harmonikusan választja el egymást5.
A feladat betűzését használva jelöljük a BD és EF, EF és AC, illetőleg AC és BD metszéspontját rendre X, Y, Z-vel, ha létrejönnek (5. ábra). Ekkor A, C és Z, Y, továbbá D, B és X, Z, végül E, F és Y, X harmonikusan választja el egymást. Ha például BEFD trapéz, akkor C felezi a rajta át a párhuzamos oldalakkal párhuzamosan húzott egyenesnek a trapézba eső szakaszát, és így AC felezi a párhuzamos oldalakkal párhuzamosan húzott minden egyenesnek az AB és AD közé eső szakaszát, tehát BD-t és EF-et is6 (6. ábra). Ezekből következik, hogy pl. az AC átmérőjű körben AZ/AY=CZ/CY, s így a kör az ehhez az arányhoz tartozó Apollóniosz-kör7.
Ezután az XYZ háromszög oldalait a C, D, E pontokban metsző egyenesre Menelaos tételét alkalmazzuk8. Eszerint, a háromszög oldalegyeneseit a háromszög valamelyik irányú körbejárása szerint irányítva
(YZC)(ZXD)(XYE)=-1.
Ebből az adódik, hogy ha két kör metszi egymást, akkor a rájuk vonatkozó távolságarányok szorzata a harmadik körre vontkozó arányt adja, vagyis a metszésponton a harmadik kör is átmegy.
Ha pl. EF és BD párhuzamos, akkor Y az EF felezőpontja, Z a BD szakaszé, és hasonló háromszögek felhasználásával fejezhető be az előzőhöz hasonlóan a bizonyítás.
3. A feladat állítását tartalmazza H. S. M. Coxeter, S. L. Greitzer Az újra felfedezett geometria címen megjelent könyvének 2.4.7 tétele9.
Surányi János

 

 

 

 

 

 
1Bár a megoldás során nem lesz rá szükség, megjegyezzük, hogy ennek az állításnak igaz a megfordítása is: minden üres háromszögnek 1/2 a területe. Ld. idevonatkozóan: Hajós Gy., Neukomm Gy., Surányi J.: Matematikai Versenytételek II. rész (Tankönyvkiadó, Budapest 1988) 107‐117. oldal.

2Elmondhatók volnának megoldásaink enélkül az egyszerűsítés nélkül is, csak a szöveg válnék sokkal bonyolultatbbá.

3Vektorokra vonatkozóan lásd pl. Hajós Gy., Neukomm Gy,. Surányi J.: Matematikai Versenytételek II. rész (Tankönyvkiadó, Budapest, 1988) 37‐47. old.; különösen e) pont, 43‐44. old.

4A bizonyítás nélkül felhasználandó ismeretekre vonatkozóan Hajós Gy. Bevezetés a geometriába c. könyvére fogunk utalni (Tankönyvkiadó, Budapest, 1960). A projektív geometria egy minimális feltételekre alapozott (a távolság, szög, folytonosság fogalmát nem használó) felépítésére vonatkozóan lásd pl. a következő művet: H. S. M. Coxeter: Projektvív geometria, Gondolat, Budapest, 1986.

5Hajós idézett műve (a továbbiakban I. m.) 460. old.

6I. m. 462‐463. old.

7I. m. 124. old.

8I. m. 357. old.

9Gondolat Kiadó, 1977., 70. old.