Kezdőlap


Cím:	Megjegyzés az Erdős-Mordell tételhez
Szerző(k):	Komornik Vilmos
Füzet:	1996/január, 4 - 5. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A Középiskolai Matematikai és Fizikai Lapok 1995. októberi számában egy érdekes cikk jelent meg az Erdős‐Mordell tétel első közlésének hatvanadik évfordulója alkalmából, bemutatva a tétel számos alkalmazását és általánosítását. (Lásd [1], [2].)
A tétel fontosságára való tekintettel talán érdeklődésre tarthat számot a cikkben közölt bizonyítás alábbi, egyszerűsített változata.

Tétel. Legyen

P

A B C

háromszög egy belső vagy határpontja. Legyen

P

távolsága a csúcsoktól rendre

R_{a}

R_{b}

R_{c}

, az oldalegyenesektől pedig rendre

r_{a}

r_{b}

r_{c}

. Ekkor fennáll az

\begin{matrix} R_{a} + R_{b} + R_{c} \geq 2 (r_{a} + r_{b} + r_{c}) \end{matrix}

(1)

egyenlőtlenség (1. ábra).
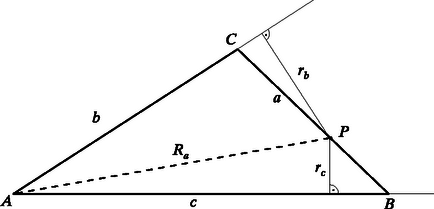
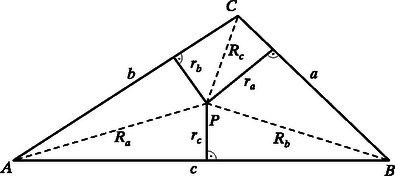
A bizonyítás három lépésből áll. A továbbiakban használjuk a szokásos

a = B C

b = C A

és

c = A B

jelöléseket.
1. Ha

P

B C

oldalon fekszik (2. ábra), akkor az

A P C

háromszög kétszeres területe

b r_{b}

-vel, az

A B P

háromszög kétszeres területe pedig

c r_{c}

-vel egyenlő, így az

A B C

háromszög kétszeres területe

b r_{b} + c r_{c}

. Másrészt

R_{a}

nem lehet rövidebb az

A B C

háromszög

A

-ból induló magasságánál, így

a R_{a}

nem lehet kisebb az

A B C

háromszög kétszeres területénél. Tehát

\begin{matrix} a R_{a} \geq b r_{b} + c r_{c} . \end{matrix}

(2)

Vegyük észre, hogy ez az egyenlőtlenség érvényben marad a

B A C

szögtartomány bármely

P

pontjára, hiszen

P

-t az

A P

félegyenes és a

B C

oldal

P'

metszéspontjára cserélve a

P'

-re vonatkozó egyenlőtlenség hasonlóság miatt ekvivalens (2)-vel.
2. Alkalmazzuk (2)-t

P

helyett annak a

B A C

szögtartomány szögfelezőjére vett

P'

tükörképére. Minthogy értelemszerű jelölésekkel

R_{a}' = R_{a}

r'_{b} = r_{c}

és

r_{c}' = r_{b}

, innen a

B A C

szögtartomány bármely

P

pontjára az

\begin{matrix} a R_{a} \geq b r_{c} + c r_{b} . \end{matrix}

(3)

összefüggést nyerjük.
3. Ha

P

A B C

háromszög belső- vagy határpontja, akkor az

a

b

c

indexek ciklikus permutálásával látható, hogy (3) mellett fennállnak a

\begin{matrix} b R_{b} \geq c r_{a} + a r_{c} és c R_{c} \geq a r_{b} + b r_{a} \end{matrix}

összefüggések is. A három egyenlőtlenséget rendre

a

-val,

b

-vel,

c

-vel leosztva, majd összeadva őket, a tétel állítása adódik:

\begin{matrix} R_{a} + R_{b} + R_{c} \geq \frac{b^{2} + c^{2}}{b c} r_{a} + \frac{c^{2} + a^{2}}{c a} r_{b} + \frac{a^{2} + b^{2}}{a b} r_{c} \geq 2 (r_{a} + r_{b} + r_{c}) . \end{matrix}

A fenti bizonyítás elemzésével könnyen látható, hogy pontosan akkor áll egyenlőség (1)-ben, ha az

A B C

háromszög szabályos és

P

a középpontja. Ennek végiggondolását az olvasóra bízzuk.

Referenciák

*	[1]Egy geometriai probléma megoldása, Középiskolai Matematikai és Fizikai Lapok, (11. évf., 1935. febr.)

*	[2]Reiman István: 60 éve jelent meg a Középiskolai Matematikai Lapokban az Erdős‐Mordell tétel, Középiskolai Matematikai és Fizikai Lapok (45. évf., 1995., 385‐394. o.)

Komornik Vilmos, Strasbourg