Cím: A mérési feladatok megoldásáról II.
Szerző(k):  Gnädig Péter 
Füzet: 1995/november, 499. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A cikk első részében1 összefoglaltuk a mérések megtervezésével, a mérési adatok gyüjtésével, táblázatba foglalásával és grafikus ábrázolásával kapcsolatos legfontosabb ismereteket. Megmutattuk, hogyan lehet a többször megismételt mérés eredményeinek ,,szórásából'' (statisztikus ingadozásából) a mérés pontosságára következtetni. Most a mérési adatok további feldolgozásával, a mérés ,,kiértékelésével'' foglalkozunk.
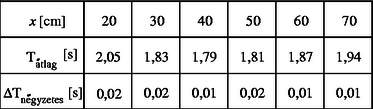
Az eljárást ugyanazon a konkrét mérési feladaton, a Nagykanizsai Nyári Fizikatábor2 egyik problémáján mutatjuk be, amelyet az első részben is idéztünk: egy nagyméretű (R=40cm sugarú) nehéz karikából fizikai ingát készítettünk, és mértük a saját síkjában kis lengéseket végző inga T lengésidejét a felfüggesztési pont és a középpont x távolságának függvényében. A mérési adatokat és azok becsült hibáját a táblázat tartalmazza.

 
  x [cm]    20 30 40 50 60 70  Tátlag [s]     2,05    1,83    1,79    1,81    1,87    1,94    ΔTnégyzet [s]     0,02    0,02    0,01    0,02    0,01    0,01  
 

Tegyük fel, hogy a mérést végző ismeri (vagy a függvénytáblázatból ki tudja keresni) a fizikai inga lengésidejét megadó
T=2πΘmgs
képletet, ahol Θ az ingának a felfüggesztési pontjára vonatkozó tehetetlenségi nyomatéka, s pedig a tömegközéppontjának és a felfüggesztési pontnak a távolsága. Jelen esetben s=x, Θ pedig az ún. Steiner-tétel szerint (amely szintén megtalálható a képletgyüjteményekben) Θ0+mx2, ahol Θ0 a tömegközéppontra (a karika középpontjára) vonatkoztatott tehetetlenségi nyomatéka, azaz jó közelítéssel mR2. Ezek szerint a lengések T periódusideje és az x távolság között fenn kell álljon a
T=2π1g⋅R2+x2x
összefüggés.
Ennyi elméleti ismeret birtokában kitűzhetjük magunk elé pl. azt a célt, hogy a mérési adatokból határozzuk meg a nehézségi gyorsulás (vagyis g) nagyságát a mérés helyszínén. (Igaz ugyan, hogy g ismert 9,81 m/s2-os értéke megtalálható a táblázatokban, de attól mi még leellenőrizhetjük, hogy valóban annyi-e!)
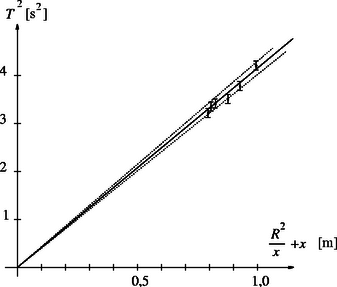
Hogyan lehet a fenti gyökös formulából és a mérési adatokból g-t meghatározni, s a kiszámított (tehát közvetett úton megmért) g-nek mennyi a mérési hibája? Erre többféle módszer is megadható, de talán a legegyszerűbb a grafikus módszer. Alakítsuk át a fenti képletet olymódon, hogy két | alkalmasan választott | mennyiség között egyenes arányosság (vagyis lineáris függvénykapcsolat) álljon fenn:
T2=4π2g⋅(R2x+x).
Látható, hogy a mérési adatokból kiszámítható T2, illetve (R2/x+x) mennyiségek egyenesen arányosak egymással, s az arányossági tényező nagyságából ki tudjuk számítani a g nehézségi gyorsulást is. Ábrázoljuk tehát T2-t (R2/x+x) függvényében, s a mérési adatoknak megfelelő pontokra illesszünk egy | az origón is átmenő | egyenest. Az ábrán a szemünknek ,,legjobban tetsző'' egyenest folytonos vonallal rajzoltuk, szaggatottan pedig azt a két egyenest, amelyiknél érzésünk szerint nem lehet meredekebb, illetve laposabb a keresett lineáris függvény. (Léteznek a szemmértéknél ,,tudományosabb'' egyenes-illesztési módszerek is, például a zsebszámológépek némelyike által is ismert Gauss-féle ,,legkisebb négyzetek módszere'', ezekkel azonban ebben a cikkben nem foglalkozunk.) Az ábráról leolvashatjuk, hogy a 4π2/g meredekség 4,1±0,1 (SI egységekben, vagyis s2/m-ben mérve), ahonnan g ,,mért értéke'' 9,6 m/s2, a hibája pedig ±0,25 m/s2. Természetesen azt is megtehettük volna, hogy a lengésidő képletéből kifejezzük g-t T és x segítségével, majd minden egyes adatpárra kiszámítjuk a nekik megfelelő g-t, és ezek számtani közepét tekintjük g mért értékének. Ezzel az eljárással azonban lemondtunk volna az adatok áttekinthető ábrázolásáról, ami pl. a feltételezett függvénykapcsolattól való esetleges eltérés könnyű felismerését teszi lehetővé. (Meg kell jegyezzük azonban, hogy a modern számítógépes méréskiértékelési eljárások grafikus ábrázolás nélkül is működőképesek, hatékonyak lehetnek.)
Mi a helyzet olyankor, amikor valahonnan tudjuk (vagy legalább sejtjük), hogy két mennyiség hatványfüggvény kapcsolatban áll egymással: y=A⋅xn, ahol A és n számunkra ismeretlen, meghatározandó állandók. Régebben általában úgy jártak el, hogy x-t és y-t úgynevezett log‐log papíron (logaritmikusan eltorzított skálájú milliméterpapíron) ábrázolták, s ott illesztettek egyenest a mérési pontokra. Manapság, amikor szinte minden diáknak van zsebszámológépe, könnyen ki tudjuk számítani a mérési adatokból az Y=logy és a X=logx mennyiségeket, s mivel a feltételezett hatványviselkedésnek az Y=n⋅X+logA lineáris függvény felel meg, visszavezettük a feladatot hagyományos milliméterpapíron elvégezhető egyenesillesztési problémára. Az egyenes meredeksége megszabja az n hatvénykitevőt, az X=0-nak megfelelő tengelymetszet pedig logA-t. Ezt a módszert (amely a log‐log papíros ábrázolással egyenértékű) azért érdemes megtanulni, mert nem csak hatvány-, hanem szinte tetszőleges alakú függvényre alkalmazható. Ha például tudjuk, hogy két mérhető mennyiség, y és x között
y=Ax2⋅e-B/x
alakú a kapcsolat, csak éppen az A és B mennyiségeket nem ismerjük, akkor a
log(y/x2)=logA-B⋅(1/x)
összefüggésből azt is tudjuk, hogy Y=log(y/x2) és X=1/x között lineáris a kapcsolat, s az Y‐X síkon illesztett egyenes adataiból le tudjuk olvasni A-t és B-t.
Említést kell még tennünk a hibaszámítás egyik fontos problémájáról, a hiba ,,öröklődésének'', a hiba terjedésének szabályairól. A korábban elemzett fizikai ingás problémánál a grafikonra illesztett egyenes k meredekségét (SI egységekben) 4,1-nek találtuk, s a hibáját ±0,1-nek becsültük. Ilyenkor azt is szokták mondani, hogy a meredekség relatív hibája 0,14,1≈0,025, azaz 2,5 % nagyságrendű. Mi következik ebből a meredekség reciprolával arányos g mennyiség pontosságára? Megtehetjük azt, hogy behelyettesítjük a g=4π2/k képletbe a meredekség két szélsőséges értékét (tehát a grafikon által még elfogadhatónak tartott legkisebb, illetve legnagyobb k számot), s ezek meghatározzák annak az intervallumnak a határait, amelyben az ,,igazi'' g benne kell legyen.
A fenti (direkt) módszer elvileg egyszerű, nem igényli a felsőbb matematika (differenciálszámítás) ismeretét, de meglehetősen időigényes. Azok kedvéért, akik már megismerkedtek a derivált függvény fogalmával, megadjuk az ,,egyszerűbb'' receptet is. Ha egy y(x) függvény független változóját egy kicsiny Δx értékkel megváltoztatjuk (x mért fizikai mennyiségnek legyen Δx a mérési hibája), akkor a belőle kiszámítható y mennyiség megváltozása (mérési hibája) jó közelítéssel
Δy≈f'(x)⋅Δx,
ahol az f'(x) deriváltat a mért (névleges) x értéknél kell képezni. Az y mennyiség abszolút hibája tehát
|Δy|=|f'(x)|⋅|Δx|
nagyságrendű. Ha például y=Axn, akkor |Δy|=Axn-1⋅|Δx|, ami a relatív hibák nyelvén sokkal egyszerűbb képletbe megy át:
Δyy=|n|⋅Δxx,
azaz n-edik hatványozásnál a relatív hiba |n|-szeresére növekszik. A fizikai inga problémájánál g a meredekség (-1)-edik hatványával arányos, tehát a relatív hibája megegyezik a meredekség 2,5 százalékos relatív hibájával: g=9,6⋅(1±0,025)=9,6±0,25 m/s2.
Kicsit bonyolultabb eset az, amikor egy | a mérési adatokból kiszámított | y mennyiséget két különböző (s mondjuk egymástól függetlenül mért) adatból (pontosabban adatsor átlagából) kapjuk meg. Gondoljunk például arra, hogy megmérjük egy l hosszúságú (matematikainak tekinthető) inga T lengésidejét, s a T=2πl/g képletből akarjuk meghatározni a nehézségi gyorsulás számértékét. Természetesen l-et is és T-t is többször mérjük, s az átlagolt l-ekből és átlagolt T-kből számítjuk ki g névleges értékét. Vajon milyen pontos lesz ez a g, ha l-et Δl, T-t pedig ΔT pontossággal ismerjük? Most is megtehetjük azt, hogy zsebszámológéppel kiszámítjuk a legnagyobb elképzelhető (a mérés pontossága alapján még elfogadható) l-hez és a hasonló értelemben vett lehető legkisebb T-hez tartozó g-t, illetve fordítva, a másik irányban menve el a legszélsőségesebb esetig, s ezekből leolvassuk g mérési hibahatárait. Van azonban egyszerűbb út is! Mivel g=4π2⋅l⋅T-2, a keresett g-nek l bizonytalanságából adódó relatív hibája megegyezik l relatív hibájával, T bizonytalanságából adódó relatív hiba pedig az időmérés relatív hibájának kétszerese. Ha például az inga hosszát 3% pontossággal ismerjük, az időt pedig 2% pontossággal tudjuk mérni, akkor az egyik ok miatt 3 százalék, a másik miatt pedig 4 százalék lesz g relatív bizonytalansága. Azt gondolhatnánk, hogy ilyenkor a mérés teljes hibáját 7%-osnak vehetjük, ez azonban nem igaz! Nagyon valószínűtlen, hogy a kétféle mérés pontatlansága mindig egymást erősítve jelentkezne, az esetek számottevő részében ,,segítenek egymáson'', a hibák részben kiejtik egymást. Ennek az a következménye, hogy az egymástól független hibaforrásokból származó relatív hibák nem adódnak simán össze, hanem a Pitagorasz-tételre emlékeztető módon négyzetesen tevődnek össze. Az előző számpéldában tehát a 3 és 4 százalékos relatív hiba együttes hatása csupán 32+42=5 százalék! Mivel azonban a mérés kiértékelésénél úgyis csak a hibák nagyságrendjét adjuk meg, nem pedig azok pontos értékét, nem követünk el nagy hanyagságot, ha a több hibaforrás együttes hatását az egyes relatív hibák algebrai összegével, vagy még egyszerűbben, a legnagyobb hibatényező nagyságrendjével közelítjük.
Külön megfontolást igényel az az eset, amikor a mérési adatokból számított végeredmény két, közel egyforma nagyságú mennyiség különbségeként áll elő. Ilyenkor az eredmény relatív hibája (a kicsiny nevező miatt) lényegesen nagyobb lehet, mint a közvetlenül mért adatok relatív hibája. A fizika történetének legpontosabb mérései olyan ötletekből születtek, amelyek valamilyen módon lehetővé tették kicsiny mennyiségek közvetlen mérését. Eötvös Loránd például nem úgy mérte meg 8 jegy pontossággal a súlyos és tehetetlen tömeg közötti esetleges kicsiny különbség nagyságát (pontosabban azt a határt, aminél biztosan nem lehet nagyobb ez a különbség), hogy 8 jegy pontossággal megmérte volna mindkét típusú tömeget, hogy kivonja azokat egymásból, hanem olyan mérési elrendezést talált, amely magára a tömegkülönbségre érzékeny, közvetlenül azt méri. Hasonló módszerrel, tehát közvetlenül a különbséget mérve határozták meg a hidrogénatom két közeli állapota közötti energiakülönbséget. Ez az úgynevezett hiperfinom átmenet, amely során kibocsátott fény frekvenciája 1420,405751782 MHz-nek adódott. A mérés relatív hibája ±1,2⋅10-12; ez a fizika (sőt, a természettudományok) történetében mindezideig a legpontosabb mérés a világon!
(G.P.)

 

 
1lásd lapunk múlt havi számában

2lásd még lapunk 503. oldalán