Cím:	Az 1995. évi (26.) Nemzetközi Fizikai Diákolimpia feladatainak megoldása I.
Szerző(k):	Gnädig Péter ,  Honyek Gyula
Füzet:	1995/október, 428 - 437. oldal	PDF  |  MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.     Elméleti verseny       1. feladat. Gravitációs vöröseltolódás és egy csillag tömegének mérése   (a) Egy $f$ frekvenciájú foton $m$ effektív tehetetlen tömegét az energiája határozza meg. Feltehetjük, hogy a súlyos (gravitációs) tömege megegyezik ezzel a tehetetlen tömeggel. Ennek megfelelően egy csillag felszínéről kibocsátott foton veszít az energiájából, amikor kiszabadul a csillag gravitációs teréből. Mutasd meg, hogy a foton $\Delta f$ frekvenciaeltolódása, miközben a foton a csillag felszínéről a végtelenbe jut, a következőképpen adható meg: $\begin{array}{c}{\displaystyle \frac{\Delta f}{f}\approx \frac{GM}{R{c}^2}\mathrm{,}}\end{array}$ amennyiben $\Delta f/f\ll f$, továbbá $G$ az univerzális gravitációs állandó, $R$ a csillag sugara, $c$ a fénysebesség, $M$ pedig a csillag tömege. így a csillagtól nagy távolságban mérve egy adott színképvonal vöröseltolódását, meghatározható az $M/R$ arány, $R$ ismerete pedig lehetővé teszi egy csillag tömegének meghatározását.   (b) Egy kísérlet során személyzet nélküli űrszondát indítanak, hogy megmérjék a Tejútrendszer egyik távoli csillagának $M$ tömegét és $R$ sugarát. Amint az űrszonda sugárirányban megközelíti a vizsgálandó objektumot, a szondán levő mérőkamra segítségével megfigyelik a csillag felszínén talalható He${}^{+}$ ionok által kibocsátott fotonokat. A kamrában He${}^{+}$ ionokból álló részecskenyaláb rezonancia-gerjesztését hozzák létre. A rezonancia-abszorpció (elnyelődés) csak akkor megy végbe, ha a He${}^{+}$ ionoknak a csillag irányába eső sebessége éppen a vöröseltolódásnak megfelelő nagyságú. A mérés során meghatározzák a He${}^{+}$ ionoknak a csillaghoz viszonyított $v=\beta c$ sebességét rezonancia-abszorpciókor a csillagfelszín (legközelebbi) $d$ távolságának függvényében. A mérési adatokat az alábbi táblázat mutatja.   $\beta =v/c$ sebesség-paraméter   $\left({10}^{-5}\right)$ 3,352  3,279  3,195  3,077  2,955 $d$  a csillagfelszín távolsága   $\left({10}^8\text{m}\right)$ 38,90  19,98  13,32  8,99  6,67   Az összes adat felhasználásával grafikus úton határozd meg a csillag $M$ tömegét és $R$ sugarát! (Itt most ne foglalkozz hibabecsléssel!)   (c) Az ilyen típusú kísérletekben gyakran a kibocsátó atom visszalökődésének frekvenciamódosító hatását is figyelembe veszik. (A hőmozgás az emissziós (kibocsátási) vonalak kiszélesedéséhez vezet, a vonal egészének eltolódása nélkül; így az előző számításainkat a termikus hatások miatt nem kell módosítanunk.) (i) Legyen $\Delta E$ egy álló atom két állapota közötti energiakülönbség. Tegyük fel, hogy egy nyugalomban lévő atom legerjesztődik, miközben egy foton jön létre és az atom visszalökődik. Határozd meg a relativisztikus formulák segítségével a kibocsátott foton $hf$ energiáját a $\Delta E$ energiakülönbség és az atom (alapállapotához tartozó) $m_0$ nyugalmi tömegének függvényében! (ii) Az így kapott formulával végezz numerikus becslést a He${}^{+}$ ionok esetében a ${\left(\Delta f/f\right)}_{\text{vissza}}$ relativisztikus frekvenciaeltolódásra. Mutasd meg, hogy ez a korrekció sokkal kisebb, mint a (b) alkérdésben kapott gravitációs vöröseltolódás. Adatok: a fénysebesség $3\cdot {10}^8$ m/s; a He atom nyugalmi energiája $m_0{c}^2=4\cdot 938$ MeV; a Bohr-energia $E_n=-13\mathrm{,}6Z^2/n^2$ eV; a gravitációs állandó $G=6\mathrm{,}7\cdot {10}^{-11}$ Nm${}^2$kg${}^{-2}$.   Megoldás. (a) Az $f$ frekvenciájú foton energiája $E=hf$ ($h$ a Planck-állandó), az ehhez társítható effektív tehetetlen tömeg pedig $m=E/c^2=hf/c^2\mathrm{.}$ Ha a foton egy $M$ tömegű, $R$ sugarú csillag felszínén jön létre, akkor az energiája (a gravitációs helyzeti energiát is figyelembe véve és a Newton-féle klasszikus gravitációs egyenletekből számolva) $E=hf-GMm/R\mathrm{.}$ Ez az energia akkor egyezik meg a csillagtól távol kerülő, tehát gravitációs helyzeti energiával nem rendelkező foton energiájával, ha annak frekvenciája $f+\Delta f$ és $\begin{array}{c}{\displaystyle hf-G\frac{M}{R}\cdot \frac{hf}{c^2}=h\left(f+\Delta f\right)\mathrm{,}}\end{array}$ ahonnan $\Delta f/f=-\left(GM\right)/\left(R{c}^2\right)$. Megjegyzés. érdekes, hogy az itt leírt ,,félklasszikus'' megfontolás ugyanazt a képletet adja a gravitációs vöröseltolódásra, mint a jelenséget sokkal ,,mélyebben'' értelmező, de matematikailag sokkal bonyolultabb általános relativitáselmélet.   (b) Az előző gondolatmenethez hasonlóan adódik, hogy a csillag közepétől $R$ távolságból induló, majd $R+d$ távolságra jutó fény relatív frekvenciaeltolódása $\begin{array}{c}{\displaystyle \frac{\Delta f}{f}=-\frac{GM}{c^2}\left(\frac{1}{R}-\frac{1}{R+d}\right)\mathrm{,}}\end{array}$ ahonnan némi átalakítással $\begin{array}{c}{\displaystyle \frac{f}{\Delta f}=-\frac{c^{2}R}{GM}-\frac{c^2{R}^2}{GM}\cdot \frac{1}{d}\mathrm{.}}\end{array}$ Mivel a Doppler-effektus szerint a fényforráshoz képest $v$ sebességgel mozgó megfigyelő $\Delta f/f=v/c=\beta$ relatív frekvenciaeltolódást észlel, a rezonancia-abszorpcióhoz szükséges mozgás $\beta$-paramétere és a csillag felszínétől mért $d$ távolság között $-1/\beta =A+B\cdot \left(1/d\right)$ az összefüggés ($A$ és $B$ állandók). ábrázoljuk a táblázatban megadott mérési adatokból kiszámítható ${\beta }^{-1}$-t $d^{-1}$ függvényében, és az adatpároknak megfelelő pontsorra illesszünk egyenest (1. ábra)! Az egyenes tengelymetszetéből megkaphatjuk a csillagra jellemző $R/M$, a meredekségéből pedig az $R^2/M$ mennyiségeket, tehát külön-külön $M$ és $R$ értékét is. A megadott adatsorból így végül $M\approx 5\mat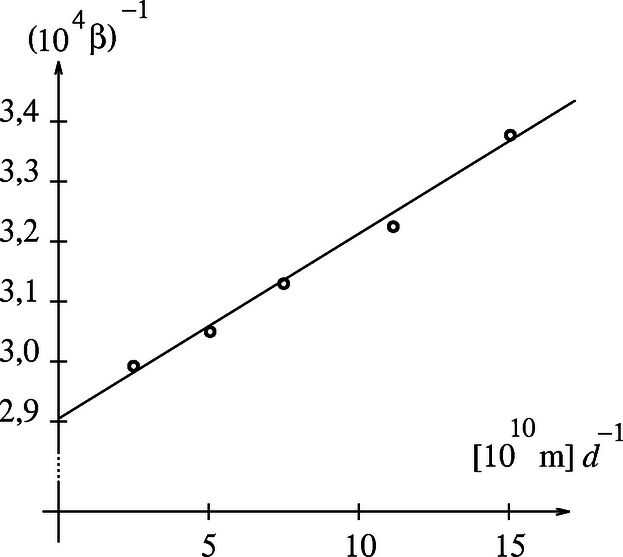hrm{,}1\cdot {10}^{30}$ kg és $R\approx 1\mathrm{,}1\cdot {10}^8$ m adódik.     1. ábra   Megjegyzés. A csillag tömegének és sugarának meghatározására nyilván van egyszerűbb módszer is. Ha az űrszonda a csillag méretével összemérhető távolságra megközelíti a csillagot, s folyamatosan méri a csillagtól mért távolságát és a csillaghoz viszonyított sebességét, akkor a megfigyelhető látószögből közvetlenül megkapható a csillag sugara, a szonda sebességének változásából pedig a csillag tömege.   (c) A visszalökődési effektusok számításánál az energia- és a lendületmegmaradás törvényére támaszkodhatunk. (i) A kezdetben álló, gerjesztett állapotban levő atom energiája $m_0{c}^2+\Delta E$, az impulzusa pedig nyilván nulla. A foton kibocsátása után a foton $p=hf/c$ impulzussal rendelkezik, tehát az atomnak is ugyanekkora nagyságú, de a fotonéval ellentétes irányú lendülete kell legyen. Az energiamegmaradás törvénye tehát a jelen esetben: $\begin{array}{c}{\displaystyle m_0{c}^2+\Delta E=hf+\sqrt[]{{\left(m_0{c}^2\right)}^2+{\left(hf\right)}^2}\mathrm{.}}\end{array}$ (Felhasználtuk a gyorsan mozgó részecskék energiája és impulzusa közötti relativisztikus $E^2=m_0^2{c}^4+p^2{c}^2$ összefüggést.) A fenti egyenletből algebrai átalakítások után $\begin{array}{c}{\displaystyle hf=\Delta E\frac{2m_0{c}^2+\Delta E}{2m_0{c}^2+2\Delta E}}\end{array}$ adódik. Ha az atomot nem engedjük visszalökődni, akkor a $\Delta E=h{f}_0$ összefüggésnek megfelelő $f_0$ frekvenciájú fotont bocsátana ki. A relatív frekvenciaeltolódás tehát a visszalökődés miatt: $\begin{array}{c}{\displaystyle {\left(\frac{\Delta f}{f}\right)}_{\text{vissza}}=\frac{f-f_0}{f_0}=-\frac{\Delta E}{2\left(m_0{c}^2+\Delta E\right)}\mathrm{.}}\end{array}$ Megjegyzés. Abban a határesetben, amikor $\Delta E\ll m_0{c}^2$ (ezt nemrelativisztikus határesetnek nevezik), a visszalökődési korrekció $-\Delta E/\left(2m_0{c}^2\right)\mathrm{,}$ amit úgy is megkaphatunk, hogy a visszalökődött atom mozgási energiáját az $E=p^2/\left(2m\right)$ nemrelativisztikus képletből számítjuk ki. A másik határesetben, amikor $\Delta E\gg m_0{c}^2$ (ezt ultrarelativisztikus határesetnek nevezik és az elemi részecskék bomlásánál gyakran megvalósul), a visszalökődési korrekció közel 50 százalékos, mert a visszalökődő rész ,,fényszerűen'' mozogva csaknem ugyanannyi energiát visz el, mint a foton. (ii) A héliumionok ($Z=2$) által az $n=2\to n=1$ átmenetben kibocsátott fotonokra $\begin{array}{c}{\displaystyle \Delta E=-13\mathrm{,}6\cdot 2^2\left(1-\frac{1}{4}\right)\approx 40\text{eV}\approx {10}^{-8}\cdot m_0{c}^2\ll m_0{c}^2\mathrm{.}}\end{array}$ A visszalökődési korrekció tehát a jelen esetben (akár a relativisztikus, akár az itt most igazán jogosan alkalmazható nemrelativisztikus képletből számoljuk) $5\cdot {10}^{-9}$ nagyságú, s ez a három nagyságrenddel nagyobb gravitációs eredetű eltolódás mellett elhanyagolható.     2. feladat. Hangterjedés   Bevezetés. Az óceánban a hang terjedési sebessége a sótartalom és a hőmérséklet változása miatt függ a mélységtől. Az 2. ábra a $c$ hangsebesség változását mutatja a $z$ mélység függvényében egy olyan helyen, ahol a hangsebesség a vízfelszín és a tengerfenék között félúton minimális, $c_0$ nagyságú. Az egyszerűség kedvéért válasszuk ezt a minimumhelyet a $z=0$ szintnek, továbbá $z=z_s$ legyen a vízfelszín, $z=z_b$ pedig a tengerfenék szintje. A $z=0$ szint felett $\begin{array}{c}{\displaystyle c=c_0+b\cdot z\mathrm{,}}\end{array}$ míg a $z=0$ szint alatt $\begin{array}{c}{\displaystyle c=c_0-b\cdot z\mathrm{.}}\end{array}$ (Mindkét esetben $b$ ugyanaz az állandó.) 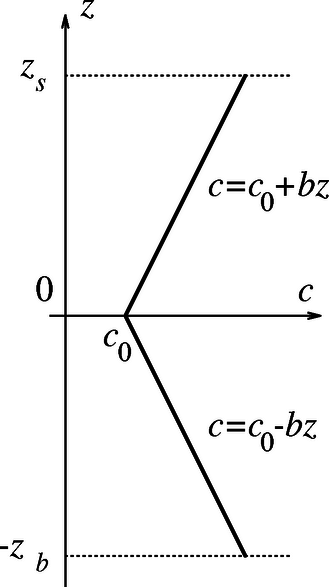    2. ábra 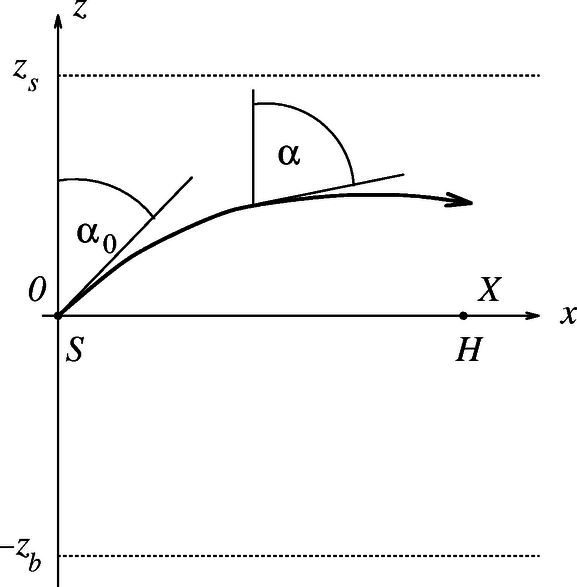      3. ábra   Az 3. ábra a $z-x$ sík egy részletét mutatja az óceánban, ahol $x$ a vízszintes irány. A $z-x$ metszet minden pontjában a $c\left(z\right)$ hangsebesség a 2. ábrának megfelelő. A $z=0$, $x=0$ helyen egy $S$ jelű hangforrást helyeztünk el. A hangforrásból ${\alpha }_0$ kezdőszöggel hangsugár lép ki. Mivel a hangsebesség $z$-vel változik, a hangsugár elgörbül, s az $\alpha$ szög értéke a pálya mentén változik.   (a) Mutasd meg, hogy a $z-x$ síkban haladó sugár pályája az $S$ forrást elhagyva, kezdetben egy $R$ sugarú körív, ahol $\begin{array}{c}{\displaystyle R=\frac{c_0}{b\text{sin}{\alpha }_0}\mathrm{,}0<{\alpha }_0<\frac{\pi }{2}\mathrm{.}}\end{array}$   (b) Vezesd le azt a kifejezést, amely $z_s$, $c_0$ és $b$ segítségével magadja azt a legkisebb lehetséges ${\alpha }_0$ értéket, amellyel felfelé elindított sugár még úgy terjedhet, hogy nem verődik vissza a víz felszínéről.   (c) A 2. ábrán egy $H$ hangérzékelő (mikrofon) is látható, a $z=0$, $x=X$ helyen. Határozd meg $b$, $X$ és $c_0$ segítségével azt az ${\alpha }_0$ szögérték-sorozatot, amely értékeknél az $S$-ből kilépő hang eljut a $H$ érzékelőhöz. Tegyük fel, hogy $z_s$ és $z_b$ elég nagy ahhoz, hogy a tengerfelszínről illetve a tengerfenékről történő visszaverődés lehetőségét kizárhassuk.   (d) Számítsuk ki (4 jegy pontossággal) ${\alpha }_0$ azon négy legkisebb értékét, amelyek esetében a hang eljut $S$-ből $H$-ba, ha $X=10000$ m, $c_0=1500$ m/s, $b=0\mathrm{,}02$ s${}^{-1}$.   (e) Határozd meg azt a formulát, amely megadja az $S$-ből $H$-ba jutó hang terjedési idejét, ha a hang pályája a (c) részben levezetett képletben szereplő legkisebb ${\alpha }_0$ szögnek felel meg. Számítsd ki ezt az időtartamot numerikusan is a (d) részben megadott adatokkal. Segítségedre lehet a következő összefüggés: $\begin{array}{c}{\displaystyle \underset{}{\overset{}{\int }}\frac{dx}{\text{sin}x}=\text{ln}\text{tg}\left(\frac{x}{2}\right)\mathrm{.}}\end{array}$ Számítsd ki az $S$-ből $H$-ba egyenesen, az $x$ tengely mentén $\left(z=0\right)$ terjedő sugárnak megfelelő időt is! A kettő közül melyik hangsugár ér oda előbb: az ${\alpha }_0=\pi /2$ szögnek megfelelően indított, vagy pedig a (d) részben kiszámított legkisebb ${\alpha }_0$-nak megfelelő?   Megoldás. (a) A helyről helyre változó hangsebességű közegben terjedő hang ,,pályája'' ugyanúgy elgörbül, mint a változó fénysebességű (azaz változó optikai törésmutatójú) közegben haladó fénysugár. Megjegyzés. Mindkét esetben akkor van csak értelme ,,sugárról'' beszélni, ha a hullámvonulat viszonylag keskeny és a terjedési sebesség csak lassan, a hullámhossznál sokkal nagyobb intervallumokon változik meg számottevően. 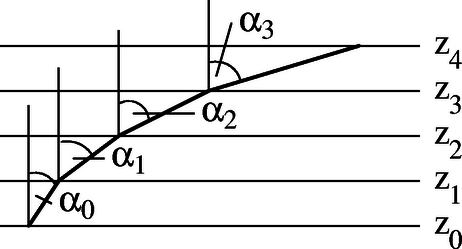    4. ábra   A folytonosan változó hangsebességű közegben haladó hang pályáját úgy számíthatjuk ki, hogy a közeget képzeletben nagyon vékony, hangtanilag homogén szeletekre vágjuk, az egyes szeletekben állandónak tekintjük a hangsebességet, a rétegek határán pedig alkalmazzuk a Snellius‐Descartes-féle törési törvényt (4. ábra): $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle \text{sin}{\alpha }_1=\text{sin}{\alpha }_0\frac{c\left(z_1\right)}{c\left(z_0\right)}\mathrm{,}}\\ \hfill {\displaystyle \text{sin}{\alpha }_2=\text{sin}{\alpha }_1\frac{c\left(z_2\right)}{c\left(z_1\right)}=\text{sin}{\alpha }_0\frac{c\left(z_2\right)}{c\left(z_0\right)}\mathrm{,}\text{...}}\end{array}}}\end{array}$ s általában 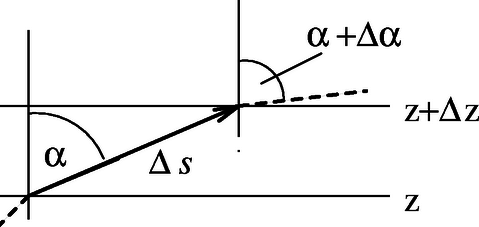$\begin{array}{c}{\displaystyle \text{sin}\alpha =\text{sin}{\alpha }_0\frac{c\left(z\right)}{c\left(0\right)}=\text{sin}{\alpha }_0\cdot \left(1+\frac{b}{c_0}z\right)\mathrm{.}}\end{array}$     5. ábra   Tekintsük most a pálya két, egymáshoz közeli pontját, amelyek egymástól $\Delta s$ távolságban vannak, a mélységük pedig $\Delta z$ értékkel különbözik (5. ábra). A törési törvény szerint a haladási iránynak a függőlegessel bezárt $\alpha$ szöge úgy változik, hogy $\begin{array}{c}{\displaystyle \text{sin}\left(\alpha +\Delta \alpha \right)-\text{sin}\alpha =\text{sin}{\alpha }_0\frac{b\Delta z}{c_0}\mathrm{,}}\end{array}$ ahonnan trigonometrikus átalakítás és a kis szögekre szokásos közelítés után (vagy differenciálszámítás alkalmazásával) kapjuk: $\begin{array}{c}{\displaystyle \text{cos}\alpha \cdot \Delta \alpha =\text{sin}{\alpha }_0\frac{b}{c_0}\Delta z\mathrm{.}}\end{array}$ Mivel $\Delta z=\Delta s\text{cos}\alpha$, továbbá tudjuk, hogy egy görbe simulókörének $R$ görbületi sugarát a $\Delta s=R\Delta \alpha$ összefüggés definiálja, leolvashatjuk, hogy $\begin{array}{c}{\displaystyle R=\frac{\Delta s}{\Delta \alpha }=\frac{c_0}{b\text{sin}{\alpha }_0}\mathrm{.}}\end{array}$ Látjuk, hogy ez a mennyiség a pálya mentén állandó, a pályagörbe tehát kör, és a sugara éppen a megadott formulának megfelelő. 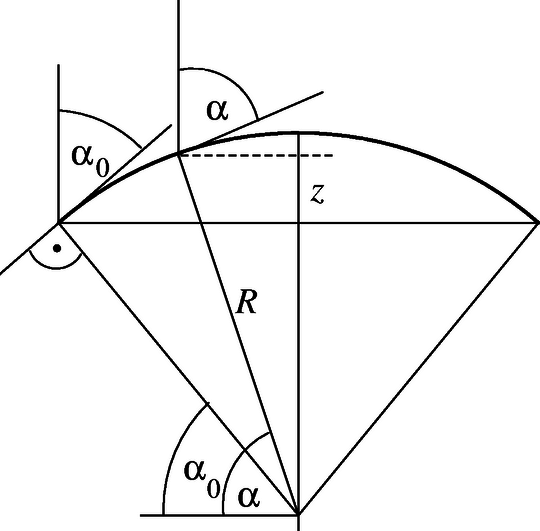    6. ábra   Más módon is beláthatjuk, hogy a hang az adott közelítésben körpályán terjed. Ha feltételezzük, hogy a pálya valamekkora sugarú kör, akkor a 6. ábráról leolvashatjuk, hogy egy tetszőleges pontbeli $\alpha$ ,,beesési szögre'' fennáll az $\begin{array}{c}{\displaystyle R\text{sin}\alpha =R\text{sin}{\alpha }_0+z\mathrm{,}}\end{array}$ vagyis a $\begin{array}{c}{\displaystyle \frac{\text{sin}\alpha }{\text{sin}{\alpha }_0}=1+\frac{z}{R\text{sin}{\alpha }_0}}\end{array}$ összefüggés. Leolvashatjuk, hogy ez a formula éppen a törési törvénynek megfelelő, a $z$ koordinátában lineáris függvénykapcsolat, ha $R$ a bizonyítandó kifejezés. Az alkalmasan választott sugarú körpálya tehát minden pontban eleget tesz a ,,hangtörés'' törvényének, s mivel a pályát a kezdeti feltételek egyértelműen meghatározzák, a megtalált megoldás a tényleges megoldás kell legyen. Nem szabad azonban megfeledkezzünk arról, hogy a hang csak addig követi a fentebb meghatározott körpályát, amíg a hangsebesség a $c=c_0+bz$ összefüggésnek megfelelően változik, vagyis ameddig $z\ge 0$.   (b) A kérdéses feltételnek akkor tesz eleget a hang pályagörbéje, ha $z_{\underset{}{\overset{}{\text{max}}}}=R-R\text{sin}{\alpha }_0<z_s\mathrm{,}$ vagyis ha $\begin{array}{c}{\displaystyle \text{sin}{\alpha }_0>1-\frac{z_s}{R}\mathrm{,}}\end{array}$ ahonnan a $\begin{array}{c}{\displaystyle \text{sin}{\alpha }_0>\frac{c_0}{c_0+b{z}_s}}\end{array}$ feltétel adódik. 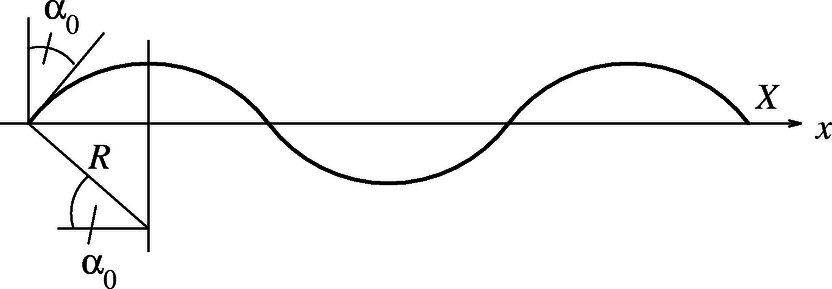      7. ábra   (c) Említettük, hogy a $z=0$ szintről felfelé elinduló hang csak addig követi a $R$ sugarú körívet, amíg vissza nem jut a hangforrással azonos mélységbe. Ezután a $z<0$ tartományban halad az ott érvényes hangsebesség-változásnak megfelelően. A pályagörbe | szimmetria-okokból | itt is egy $R$ sugarú körív lesz, amely azonban most felfelé kanyarodik. A hang tehát egymást váltogató körívek mentén terjed (lásd a 7. ábrát), és ha az ${\alpha }_0$ indulási szöget alkalmas módon választjuk, el is juthat az $x=X$ helyen található mikrofonba. Ennek az a feltétele, hogy $\begin{array}{c}{\displaystyle 2R\text{cos}{\alpha }_0\cdot n=X\mathrm{,}\left(n=\mathrm{1,}\mathrm{2,}\mathrm{3,}\text{...}\right)}\end{array}$ amit $\begin{array}{c}{\displaystyle \text{tg}{\alpha }_0=\frac{2c_0}{Xb}n}\end{array}$ alakba is írhatunk.   (d) A fenti formulába behelyettesítve a megadott számértékeket a $\text{tg}{\alpha }_0=15n$ összefüggéshez jutunk, amelynek $n=\mathrm{1,2,3}$ és $4$-hez tartozó megoldásai: ${\alpha }_0=86\mathrm{,}{19}^{\circ };$ $88\mathrm{,}{09}^{\circ };$ $88\mathrm{,}{73}^{\circ }$ és $89\mathrm{,}{05}^{\circ }\mathrm{.}$   (e) Határozzuk meg, hogy mennyi idő alatt teszi meg a hang az 5. ábrán látható kicsiny $\Delta s=R\Delta \alpha$ hosszúságú szakaszt! Mivel ezen a rövid intervallumon a hangsebesség állandónak tekinthető, a kérdéses idő $\begin{array}{c}{\displaystyle \Delta t=\frac{\Delta s}{c\left(\alpha \right)}=\frac{R\text{sin}{\alpha }_0}{c_0}\cdot \frac{\Delta \alpha }{\text{sin}\alpha }=\frac{1}{b}\cdot \frac{\Delta \alpha }{\text{sin}\alpha }\mathrm{.}}\end{array}$ összegezzük ezeket a kicsiny időtartamokat az első körív ,,felszálló ágára'', vagyis amíg $\alpha$ értéke ${\alpha }_0$-ról $\pi /2$-re növekszik. Ez az idő a hang $S$-ből $H$-ba jutási idejének, $T$-nek $2n$-ed része, ha ${\alpha }_0$ az $n$ számú körívnek megfelelő indulási szög. így tehát a terjedés ideje $\begin{array}{c}{\displaystyle T\approx 2n\cdot \sum _{}^{}\Delta t=\frac{2n}{b}\sum _{}^{}\frac{\Delta \alpha }{\text{sin}\alpha }\approx \frac{2n}{b}\underset{{\alpha }_0}{\overset{\pi /2}{\int }}\frac{d\alpha }{\text{sin}\alpha }=\frac{-2n}{b}\text{ln}\text{tg}\frac{{\alpha }_0}{2}\mathrm{.}}\end{array}$ Numerikusan $n=1$ esetén $T_1=6\mathrm{,}6662$ s adódik, míg az egyenes pályán való terejedés ideje: $T_0=X/c_0=6\mathrm{,}6667$ s. Megjegyzések. 1. Meglepőnek tűnhet, hogy a hang a körív mentén hamarabb elér $S$-ből $H$-ba, mint az egyenes (és emiatt nyilván rövidebb) úton. Ennek az a magyarázata, hogy a $z$ tengelytől eltávolodva a hangsebesség megnő, s ez a sebességnövekedés még hosszabb út esetén is eredményezhet rövidebb terjedési időt. 2. A Fermat-elv szerint két adott pont között úgy terjednek a hullámok (legyen a hullám akár fény, akár hang), hogy a ,,legrövidebb idő'' alatt jusson el a ,,célba''. Hogyan egyeztethető össze ezzel a kijelentéssel az a számítási eredmény, miszerint a hang két különböző pályán is eljut $S$-ből $H$-ba, és a kétféle pályán a terjedési idők különbözőek, tehát mindkettő nem lehet ,,a legrövidebb''! A paradoxon feloldását a Fermat-elv pontosabb megfogalmazása nyújtja: a hullámok úgy terjednek, hogy a tényleges pályán való haladás ideje jó közelítéssel megegyezik a ténylegeshez közeli pályáknak megfelelő időkkel. Ezt a feltételt mindkét hanghullám (az egyenes és a körív menti is) külön-külön teljesíti, de egymással nem szabad összevetnünk a kétféle pályaidőt, mert ez a két pálya nincs közel egymáshoz!   3. feladat. Henger alakú bója   (a) Egy $r$ sugarú, $l$ hosszúságú, tömör, henger alakú, homogén tömegeloszlású bója nagyon könnyű, $d$ sűrűségű anyagból készült. A bójának további része egy homogén, merev rúd, amely a hengeres rész közepénél a henger tengelyére merőlegesen nyúlik ki a hengerpalástból. A rúd tömege megegyezik a henger tömegével, a hossza pedig ugyanakkora, mint a henger átmérője. A rúd sűrűsége sokkal nagyobb, mint a tengervízé, a rúd átmérője pedig elhanyagolhatóan kicsi. Ez a bója $\rho$ sűrűségű tengervízben úszik. Vezesd le azt az összefüggést, amely megadja a 8. ábrán látható $\alpha$ úszási szöget $d/\rho$-val kifejezve. 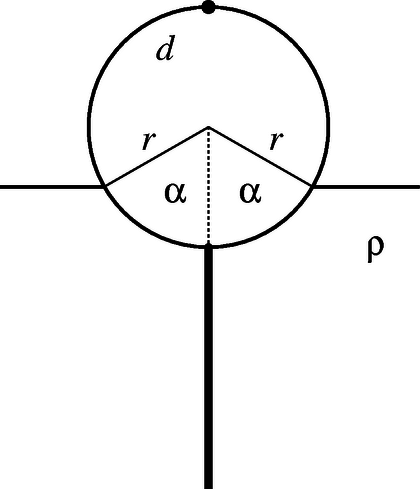    8. ábra     (b) Ha valamilyen zavar következtében a bója egy kicsiny $z$ értékkel függőlegesen lesüllyed, eredő emelőerőt fog érezni, aminek következtében föl-le rezegni kezd az úszási egyensúlyi helyzete körül (9. ábra). Határozd meg ennek a függőleges rezgésnek a frekvenciáját $\alpha \mathrm{,}$ $g$ és $r$ segítségével ($g$ a gravitációs gyorsulás). A víz mozgásának hatását úgy vehetjük figyelembe, mintha a bója tömege az eredeti érték 1/3-ával megnövekedne. Felteheted, hogy az $\alpha$ szög nem nagyon kicsi. 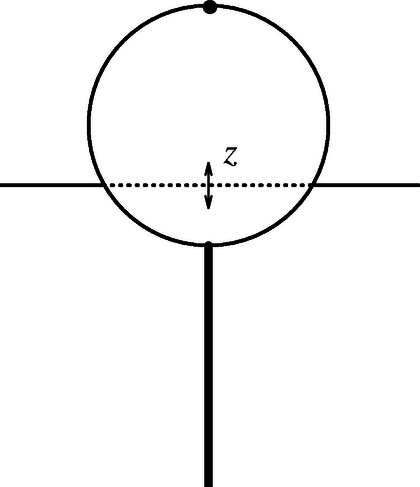    9. ábra     (c) Abban a közelítésben, hogy a henger vízszintes szimmetriatengelye körül végez ingaszerű lengéseket (10. ábra), határozd meg a lengés frekvenciáját ismét $g$ és $r$ segítségével! Hanyagold el a víz mozgását és belső súrlódását ebben az esetben! Feltételezhető, hogy a lengések szöge kicsi. 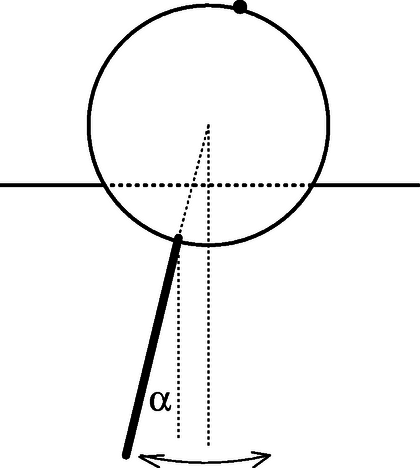    10. ábra     (d) A bójában érzékeny gyorsulásmérőket helyeztek el, melyek a függőleges és a lengő mozgást mérik, és az adatokat rádió segítségével továbbítják a partra. Viszonylag nyugodt vízben azt észleljük, hogy a függőleges rezgés periódusideje 1 másodperc körüli, míg a lengés periódusideje $1\mathrm{,}5$ másodperc körüli érték. Ebből az információból kiindulva mutasd meg, hogy az $\alpha$ úszási szög közel ${90}^{\circ }$, majd határozd meg a bója sugarát és teljes tömegét annak ismeretében, hogy a henger $l$ hossza $r$-rel egyenlő. Közelítő adatok: $\rho =1000$ kg/m${}^3$ és $g=9\mathrm{,}8$ m/s${}^2\mathrm{.}$   Megoldás. (a) A bója súlya a hengeres rész súlyának kétszerese, vagyis $\begin{array}{c}{\displaystyle G_{\text{b}}=2\cdot r^2\pi lgd\mathrm{.}}\end{array}$ A kiszorított víz súlya $\begin{array}{c}{\displaystyle G_{\text{v}}=l{r}^2\left(\alpha -\text{sin}\alpha \text{cos}\alpha \right)\rho g\mathrm{.}}\end{array}$ Az úszás egyensúlyi feltétele szerint $G_{\text{b}}=G_{\text{v}}$, ahonnan a keresett összefüggés: $\begin{array}{c}{\displaystyle \alpha -\text{sin}\alpha \text{cos}\alpha =2\pi \frac{d}{\rho }\mathrm{.}}\end{array}$   (b) A bója merülési mélységét kicsiny $z$ értékkel megnövelve a vízbe merülő rész térfogata közelítőleg $2zlr\text{sin}\alpha$ értékkel növekszik, a többlet felhajtóerő tehát $\begin{array}{c}{\displaystyle F=-2zlr\rho g\text{sin}\alpha =-k\cdot z\mathrm{.}}\end{array}$ Ez az erőtörvény ugyanolyan alakú, mint egy $k$ rugóállandójú rugóé, a bója mozgása tehát harmonikus rezgőmozgás lesz és a periódusidő $\begin{array}{c}{\displaystyle T_1=2\pi \sqrt[]{\frac{m_{\text{eff}}}{k}}\mathrm{,}}\end{array}$ ahol $\begin{array}{c}{\displaystyle m_{\text{eff}}=\frac{4}{3}{m}_{\text{bója}}=\frac{8}{3}{r}^2\pi ld}\end{array}$ a rezgő rendszer úgynevezett effektív tömege. A fentiek szerint a függőleges rezgés periódusideje: $\begin{array}{c}{\displaystyle T_1=2\pi \sqrt[]{\frac{2r\left(\alpha -\text{sin}\alpha \text{cos}\alpha \right)}{3g\text{sin}\alpha }}\mathrm{.}}\end{array}$ Megjegyzés. A fenti gondolatmenettel kapott eredmény csak fenntartásokkal fogadható el! A fel és lefele mozgó víz hatása ugyanis nem csak a rezgő rendszer tömegének látszólagos megnövekedésében jelentkezik, hanem a keletkező hullámok által elvitt energia csillapításában is. Ez a csillapító hatás még akkor is fellépne, ha a víz belső súrlódása elhanyagolhatóan kicsi lenne (ideális folyadék közelítés), s a rezgés amplitúdójának fokozatos csökkentése mellett a rezgés frekvenciáját is módosítja.   (c) A javasolt közelítésben a rendszer fizikai ingaként kezelhető, melynek lengésideje $\begin{array}{c}{\displaystyle T_2=2\pi \sqrt[]{\frac{\Theta }{D}}\mathrm{,}}\end{array}$ ahol $\begin{array}{c}{\displaystyle \Theta =\frac{1}{2}{m}_{\text{henger}}{r}^2+\frac{1}{3}{m}_{\text{rúd}}{r}^2+m_{\text{rúd}}{\left(2r\right)}^2}\end{array}$ a rendszer teljes tehetetlenségi nyomatéka a henger tengelyére vonatkoztatva, $D$ pedig a kicsiny $\alpha$ szögelforduláshoz tartozó $\begin{array}{c}{\displaystyle M\left(\alpha \right)=-2mgr\alpha =-D\cdot \alpha }\end{array}$ forgatónyomaték-képletben szereplő állandó (az ún. direkciós nyomaték). Ezen összefüggések felhasználásával a lengésidő: $\begin{array}{c}{\displaystyle T_2=2\pi \sqrt[]{\frac{29r}{12g}}\mathrm{.}}\end{array}$ Megjegyzés. Fel kell hívnunk a figyelmet arra, hogy a fenti közelítés nem áll összhangban a fizika alaptörvényeivel, nevezetesen Newton II. törvényével, s emiatt a vizsgált jelenségnél még közelítő megoldásként sem fogadható el! Ha ugyanis a bója a megadott módon mozogna, akkor a tömegközéppontja (ami a rúd és a hengerpalást érintkezési pontjánál van) vízszintes irányban is gyorsulna, noha vízszintes irányú erő nem hat a rendszerre! A feladat szövegében leírt mozgás csak külső kényszer, a bója hengere szimmetriatengelyének rögzítésével érhető el a valóságban. A fizikai jelenségek leírásánál gyakran alkalmazunk közelítéseket (pl. a lejtőn csúszó testre ható súrlódási erőt, vagy az áramkörök vezetékeinek ellenállását a számolás során legtöbb esetben elhanyagoljuk). Ezek a közelítések azonban fizikailag lehetséges (és elvben tetszőleges pontosan megvalósítható) helyzeteket írnak le, és sohasem mondanak ellent a fizika elfogadott, kísérletileg sokszorosan ellenőrzött alaptörvényeinek. ${}^{*}$Sajnálatos, hogy a Nemzetközi Fizikai Diákolimpia zsűrije | néhány tag határozott tiltakozása ellenére | a közölt formában fogadta el a feladat szövegét, s ezzel több (közöttük néhány magyar) versenyzőt is alaposan megzavart.   (d) A kétféle periodikus mozgás rezgésidejének aránya a megadott számadatok szerint: $T_2/T_1\approx 1\mathrm{,}5.$ Az előzőekben kapott összefüggéseket ebbe az egyenletbe helyettesítve az úszási szögre a $\begin{array}{c}{\displaystyle \frac{\alpha -\text{sin}\alpha \text{cos}\alpha }{\text{sin}\alpha }\approx \frac{29}{18}}\end{array}$ feltételt kapjuk, s ennek $\alpha ={90}^{\circ }=\pi /2$ valóban jó közelítéssel eleget tesz. A bója sugarára a megadott számokból $0\mathrm{,}23$ m, a tömegére pedig 20 kg adódik. A kísérleti verseny feladatait jövő hónapban közöljük. Gnädig Péter Honyek Gyula     Kísérleti verseny       1. feladat. Merülési sebesség súrlódó folyadékban   Egy folyadékban süllyedő tárgy előbb-utóbb állandó sebességet ér el, amit merülési sebességnek nevezünk. Ebben a kísérletben glicerinben süllyedő tárgyak merülési sebességét kell meghatároznod. Ha egy $r$ sugarú gömb $v$ sebességgel mozog súrlódó folyadékban, a közegellenállási erő $F=6\pi \eta rv\mathrm{,}$ ahol $\eta$ a folyadék viszkozitása. Ebben a kísérletben fémhengerek merülési sebességét kell mérned (a szokásos gömbök vizsgálata helyett). Mindegyik henger átmérője megegyezik a magasságával. Feltesszük, hogy az ilyen alakú hengerre ható közegellenállási erő képlete hasonló az ugyanakkora ($2r$ átmérőjű) gömbre ható erő képletéhez, nevezetesen: $\begin{array}{c}{\displaystyle F_{\text{henger}}=6\pi \kappa \eta r^{m}v\mathrm{.}}\end{array}$ (Gömb esetén ebben az összefüggésben $\kappa =\mathrm{1,}m=1$ szerepelne.)   Előzetes feladat: a merülési sebesség számítása.   Ha $\rho$ a henger sűrűsége és $\rho \text{'}$ a folyadéké, igazold, hogy a $v$ merülési sebesség a következő alakú: $\begin{array}{c}{\displaystyle v=C{r}^{3-m}\left(\rho -\rho \text{'}\right)\mathrm{,}}\end{array}$ ahol $C$ állandó. Add meg a $C$ állandót leíró kifejezést is!   A mérés   A rendelkezésre álló eszközök segítségével határozd meg számszerűen az $m$ kitevőt és a glicerin sűrűségét!   Megjegyzések. 1. Az egyértelműség kedvéért ügyelj arra, hogy mindig azonos helyzetből és azonos állásból (vízszintes tengellyel) indítsd a hengereket! 2. A hengerek méretét $0\mathrm{,}05$ mm pontossággal ismerjük; nem szükséges neked is megmérned! 3. Egy nyeles emelőszita segítségével a fémhengereket kiemelheted a glicerinből. Ne felejtsd el a szitát az ejtéseid előtt a glicerinbe meríteni, különben nem tudod folytatni a mérést. 4. A glicerin a levegőből vizet vehet fel, ami a viszkozitását csökkentheti. Ezért a mellékelt műanyag fóliával takard le a glicerines mérőhengert, amikor nem mérsz. 5. Ne keverd össze a különböző méretű és különböző anyagú fémhengereket!   Sűrűség-adatok   A mérés során használt fémek sűrűsége ${10}^3$ kg/m${}^3$ egységekben: alumínium $2\mathrm{,}70$; titán $4\mathrm{,}54$; acél $7\mathrm{,}87$; réz $8\mathrm{,}96$.   Mérőeszközök   * |1 db 1000 ml térfogatú mérőhenger, glicerinnel töltve, * |1 db glicerint tartalmazó edény a mérőhenger teletöltéséhez, * |1 db elektronikus stopper, * |1 db 30 cm-es vonalzó, * |1 db ruhacsipesz, * |1 db nyeles szita a fémhengerek kiemeléséhez, * |1 db műanyag csipesz, * |6 db $10\mathrm{,}00$ mm átmérőjű alumínium henger, * |6 db $8\mathrm{,}00$ mm átmérőjű alumínium henger, * |6 db $5\mathrm{,}00$ mm átmérőjű alumínium henger, * |6 db $4\mathrm{,}00$ mm átmérőjű alumínium henger, * |6 db $4\mathrm{,}00$ mm átmérőjű titán henger, * |6 db $4\mathrm{,}00$ mm átmérőjű acél henger, * |6 db $4\mathrm{,}00$ mm átmérőjű réz henger, * |lineáris és log‐log milliméterpapírok.   Megoldás. A merülési sebességet a test súlyának, a felhajtóerőnek és a közegellenállási erőnek az egyensúlya határozza meg: $\begin{array}{c}{\displaystyle r^2\pi \cdot 2r\cdot \rho g-r^2\pi \cdot 2r\cdot \rho \text{'}g-6\pi \kappa \eta r^{m}v=\mathrm{0,}}\end{array}$ ahonnan $\begin{array}{c}{\displaystyle v=\frac{g}{3\kappa \eta }\cdot r^{3-m}\left(\rho -\rho \text{'}\right)=C\cdot r^{3-m}\left(\rho -\rho \text{'}\right)\mathrm{.}}\end{array}$ A mérést úgy végezhetjük el, hogy a glicerinnel töltött hengerbe különböző sugarú és különböző sűrűségű fémhengereket ejtünk, majd megmérjük, hogy a lefelé süllyedő testek mennyi idő alatt haladnak át két, a mérőhenger falán előre bejelölt szintvonal között. A távolság és időtartam mért értékeiből kiszámítjuk a test (átlag)sebességét. A felső szintvonal helyzetét változtatva az átlagsebesség nagyságának változatlanságából megállapíthatjuk, hogy a süllyedő testek már viszonylag hamar, kb. 1 cm-es út megtétele után egyenletesen mozognak. A feladat szövege utal arra, hogy a mérés során a glicerin viszkozitása a higroszkóposság miatt fokozatosan megváltozhat. Az ebből származó szisztematikus hibát úgy csökkenthetjük, hogy a különböző sugarú és különböző sűrűségű fémhengereket (mindegyikből 6‐6 állt rendelkezésre) véletlenszerűen kiválasztott sorrendben ejtjük a glicerinbe. A mérési adatok kiértékelését úgy kezdjük, hogy az azonos $r$ és $\rho$ értékekhez tartozó mért sebességeknek (legalább 6‐6 adat) számtani közepét képezzük, illetve az ettől való (átlagos négyzetes) eltérés nagyságából megbecsüljük az egyes mérések hibáját. A következő lépésben kiválasztjuk a különböző sugarú, de azonos sűrűségű (alumínium) hengerek merülési sebességi adatait. Mivel ekkor $v\sim r^{3-m}\mathrm{,}$ ábrázolva $v$-t $r$ függvényében log‐log papíron (vagy $\text{log}v$-t $\text{log}r$ függvényében lineáris milliméterpapíron), a mérési pontokra illeszthető egyenes meredekségéből $3-m\mathrm{,}$ tehát $m$ is leolvasható. Ezzel az eljárással a keresett kitevőre $m=1\mathrm{,}34\pm 0\mathrm{,}05$ adódott. ábrázoljuk most a különböző sűrűségű, de azonos sugarú (4 mm-es átmérőjű) hengerek merülési sebességét a sűrűségük függvényében. Mivel most $v\sim \left(\rho -\rho \text{'}\right)\mathrm{,}$ a mérési adatokra illesztett egyenes tengelymetszete (vagyis a $v=0$ értékhez tartozó extrapolált sűrűségérték) a glicerin keresett sűrűségét adja. Numerikusan $({10}^3$kg/m${}^3$ egységekben): $\rho \text{'}=1\mathrm{,}1\pm 0\mathrm{,}2$. (Ez a sűrűségmérési ,,eljárás'' meglehetősen pontatlan. A táblázatokban szereplő érték, melyet pl. úszó sűrűegmérővel sokkal egyszerűbben és pontosabbann lehet ellenőrizni: $1\mathrm{,}26\cdot {10}^3\text{kg}/{\text{m}}^3$. Megjegyzés. A feladat szövegében javasolt közegellenállási képlet, miszerint $F$ a sebességtől lineárisan, a henger méretétől viszont $r^m$ $\left(m\ne 1\right)$ alakban függ, meglehetősen önkényes és elméletileg teljesen megalapozatlan! Ha az $r$ sugarú, $2r$ magasságú, $\rho \text{'}$ sűrűségű és $\eta$ viszkozitású folyadékban $v$ sebességgel egyenletesen mozgó hengerre ható közegellenállási erőt $\begin{array}{c}{\displaystyle F_{\text{henger}}=6\pi \eta rv\cdot f\left(r\mathrm{,}\rho \text{'}\mathrm{,}\eta \mathrm{,}v\right)}\end{array}$ alakban keressük, akkor (dimenzionális okokból) nyilvánvaló, hogy a dimenziótlan $f$ mennyiség a 4 változójától nem akárhogyan, hanem csak az ugyancsak dimenziótlan $R=rv\rho \text{'}/\eta$ kombináción (az ún. Reynolds-számon) keresztül függhet. Ha ezt a függést $f\left(R\right)=C\cdot R^{\lambda }$ hatványfüggvény alakban keressük, akkor a közegellenállási erőre az $\begin{array}{c}{\displaystyle F\left(r\mathrm{,}v\mathrm{,}\rho \text{'}\mathrm{,}\eta \right)\sim r^{\lambda +1}{v}^{\lambda +1}{\eta }^{1-\lambda }{\left(\rho \text{'}\right)}^{\lambda }}\end{array}$ kifejezést kapjuk. (A sebesség négyzetével és a keresztmetszettel arányos ismert turbulens közegellenállási képletnek pl. $\lambda =1$ felel meg.) A merülési sebesség a fenti közegellenállási képlet szerint $\begin{array}{c}{\displaystyle v=C{r}^{\frac{2-\lambda }{1+\lambda }}\cdot {\left(\rho -\rho \text{'}\right)}^{\frac{1}{\lambda +1}}}\end{array}$ alakú. A $r$ változótól való függésből meghatározható a $\lambda$ kitevő és numerikusan kb. $0\mathrm{,}13$ adódik. Eszerint rögzített $r$ esetén $v^{1\mathrm{,}13}\sim \left(\rho -\rho \text{'}\right)$; tehát a sebesség megfelelő hatványának lineáris $\rho$-függéséből meghatározhatjuk a folyadék sűrűségét. A kétféle kiértékelési mód között mindössze a $\rho$-függés kicsit eltérő hatványkitevőjében mutatkozik eltérés; ez az eltérés azonban olyan kicsi (10 százaléknyi), hogy a mérésben elérhető pontosság mellett nem könnyen vehető észre.   2. feladat. Lézerfény elhajlása és szóródása (KöZVETLENüL NE NéZZ A LéZERSUGáRBA ─ MARADANDó LáTáSCSöKKENéST OKOZHAT!)   Ebben a kísérletben a fény visszaverődésének, elhajlásának és szóródásának néhány esetét vizsgáljuk félvezető lézer látható fénye segítségével. Egy fémvonalzót használunk visszaverődési optikai rácsként. Egy plexiből készült és vizet illetve vízzel hígitott tejet tartalmazó kicsiny tartály segítségével vizsgáljuk a fényvisszaverődési és -szóródási jelenségeket.   1. rész. Helyezd el a mellékelt, 150 mm hosszúságú fémvonalzót úgy, hogy a fényezett oldala közel merőleges legyen a beeső lézersugárra, és a lézersugár számos osztásrészt világítson meg rajta! A mellékelt fehér papírernyőn fényelhajlás segítségével állíts elő ,,fényfolt-sorozatot''. Mérd meg ezeknek a foltoknak a helyét és egymástól való távolságát a kb. másfél méterre elhelyezett ernyőn! Rajzold le vázlatosan az általad alkalmazott elrendezést! Használd fel a következő összefüggést: $\begin{array}{c}{\displaystyle N\lambda =\pm h\text{sin}\beta \mathrm{,}}\end{array}$ ahol $N$ az elhajlás rendje, $\lambda$ a fény hullámhossza, $h$ a rácsállandó és $\beta$ az elhajlás szöge. Mérési eredményeid alapján határozd meg a lézerfény hullámhosszát és ennek mérési hibáját!   2. rész. Helyezd el a plexitartályt üresen a lézer és a fehér papírernyő közé! állítsd a tartályt közel merőlegesen a lézersugár irányára! (i) Figyeld meg, hogy az áthaladó sugár intenzitása lecsökken. Becsléssel határozd meg, hogy hány százalékos ez a csökkenés. Néhány hitelesített fényszűrő segít a becslésnél. Vedd figyelembe, hogy az emberi szem ingerületi érzékelése a jel logaritmusával arányos! A fény intenzitásának csökkenését elsődlegesen a levegő‐plexi határfelületen bekövetkező visszaverődési veszteségek okozzák, összesen négy alkalommal. Merőleges beesésnél az $R$ visszaverődési tényező (a visszavert és beeső sugár intenzitásának aránya) minden egyes felületen az $\begin{array}{c}{\displaystyle R=\frac{{\left(n_1-n_2\right)}^2}{{\left(n_1+n_2\right)}^2}}\end{array}$ formulával számolható, ahol $n_1$ a beesés előtti, $n_2$ pedig a beesés utáni közeg törésmutatója. A megfelelő áteresztési együttható (a plexiben történő elnyelődést elhanyagolva): $T=1-R$. (ii) Felhasználva, hogy a plexi törésmutatója $1\mathrm{,}59$ értékű, és elhanyagolva a többszörös visszaverődéseket, valamint a koherencia-hatásokat, számítsd ki az üres plexitartály fényáteresztési tényezőjét! Hasonlítsd össze ezt az eredményt az (i) részben végzett becsléseddel!   3. rész. Anélkül, hogy a plexitartályt elmozdítanád, töltsél a mellékelt pohárból 50 ml vizet a tartályba, és ismételd meg a 2. részben végzett megfigyeléseidet és számításaidat. (A víz törésmutatója $1\mathrm{,}33$).   4. rész. (i) Adagoljál 0,5 ml (12 csepp) tejet (fényszóró anyagot) a plexitartályban levő 50 ml vízhez és alaposan keverd fel! Mérd meg a lehető legpontosabban a lézerfény szóródási kúpjának teljes nyílásszögét és a tartály túlsó oldalán létrejövő fényfolt átmérőjét (ezek az adatok nem függetlenek egymástól). Adjál becslést az átmenő fény intenzitásának gyengülésére is az előző részfeladatokhoz hasonlóan.   (ii) Adagoljál további 0,5 ml tejet a tartályba és ismételd meg az (i) alkérdésben szereplő méréseket!   (iii) Ismételd meg többször a (ii) alkérdésbeli eljárást, egészen addig, amíg nagyon kevés vagy semennyi lézerfény sem jut át a tartályon.   (iv) Határozd meg a tej koncentrációja és a teljes szóródási szög közötti kapcsolatot!   (v) Tudjuk, hogy $I=I_0\cdot e^{-\mu z}=T_{\text{tej}}\cdot I_0\mathrm{,}$ ahol $I_0$ a bejövő intenzitás, $I$ az áthaladó intenzitás, $z$ a tartály szélessége, $\mu$ a gyengítési tényező (ez arányos a fényt szóró részecskék koncentrációjával), $T_{\text{tej}}$ pedig a tej fényáteresztési tényezője. A mérési adataid és a fenti formula segítségével becsüld meg, mekkora lehet $\mu$ értéke 10 százalékos tejkoncentráció esetén!   Mérőeszközök (Nem szükséges valamennyi eszközt felhasználnod!)   * |Lézerdióda fényforrás, * |fémvonalzó, mint diffrakciós optikai rács, * |plexitartály, ami vizet és tejet tárol, fényvisszaverődés és fényszórás tanulmányozására, * |mérőszalag, * |fehér papírból készült ernyő, * |szórólencsék, * |gyűjtőlencsék, * |szögmérő, * |fényszűrők, * |pohár és szemcseppentő, * |keverő, * |lineáris és log‐log milliméterpapírok.   Megoldás. A feladat szövegének részletes útmutatása, a kiértékeléshez szükséges megadott képletek alapján a mérés lépésről lépésre elvégezhető. Mivel elvileg viszonylag egyszerű, a megvalósítását tekintve viszont meglehetősen bonyolult ez a mérés, a megoldás részletes ismertetése helyett csak néhány technikai részletre hívjuk fel a figyelmet. 1. A fémvonalzó osztásai egymástól 0,5 mm távolságban helyezkednek el, s ez optikai szempontból nagyon durva rács. Emiatt az elhajlási maximumok nagyon kicsiny szögben, a másfél méternyire levő ernyőn kb. milliméterenként követik egymást és emiatt nehezen és pontatlanul mérhetők. Sokkal szerencsésebb elrendezés az, amikor a lézerfény nem merőlegesen, hanem laposan, csaknem 90 fokos beesési szögben éri a vonalzót. Ekkor az elhajlási rendek jól szétválnak az ernyőn és a helyzetük sokkal pontosabban mérhető. (Sajnos ezt a mérési elrendezést a feladat szövege kizárta.) 2. A fényerősség mérésére a szem csak ,,nullműszerként'' alkalmas; meglehetősen pontosan (akár százaléknyi pontossággal) el tudjuk dönteni, hogy két közeli felület mikor ugyanolyan ,,világos'' (lásd pl. a Bunsen-féle zsírfolt-fotométert részletesebben Budó‐Mátrai: Kísérleti Fizika III. kötet 270.§.). A fényerősség nagyságának számszerű meghatározására, két ismert megvilágítottság közötti érték interpolálására azonban a szem nem, vagy csak nagyon pontatlanul képes. Becsléssel a versenyzők csak annyit tudtak megállapítani, hogy a plexitartályon áthaladó fény valamennyit gyengül, de nem annyit, mint amikor egy 75 százalékos fényszűrőt helyeztek a fény útjába. A megadott formulából kiszámított érték $T=0\mathrm{,}80$. 3. Az említett okok miatt a vízzel, illetve tejes vízzel töltött tartály fényáteresztési képességét sem lehetett a megadott eszközökkel számottevő pontossággal megmérni. Ugyancsak gondot okozott a szóródási kúp nyílásszögének meghatározása. A kolloid részecskéken szóródó lézerfény ugyanis nem egy éles határvonalú kúp mentén szélesedik ki, hanem egy elmodódott szélű fényfoltot rajzol ki az ernyőn, s ennek méretét szemrevételezéssel csak nagyon önkényesen lehet meghatározni. 4. A mérési feladat kitűzőinek állítása szerint mind a szóródási szög, mind pedig a tej $\mu$ gyengítési tényezője a vizsgált tartományban egyenesen arányos a tej koncentrációjával, s ezt a lineáris függvényt extrapolálhatjuk a 10 százalékos koncentrációnak megfelelő mérhetetlenül gyenge áthatoló fény esetére is. Ennek az állításnak kísérleti eredményekkel történő alátámasztásáig azonban az említett nehézségek miatt a versenyzők többsége nem jutott el. Gnädig Péter ${}^{*}$${}^1$