Kezdőlap


Cím:	1994. Centenáriumi Eötvös-verseny
Szerző(k):	Radnai Gyula
Füzet:	1995/április, 237 - 248. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1994-ben nemcsak a Lapok, hanem az Eötvös verseny is centenáriumot ünnepelt: éppen 100 évvel ezelőtt, 1894-ben indította útjára a Tanulóversenyt a Mathematikai és Physikai Társulat. Ezzel akarták - és sikerült - emlékezetessé tenni azt a tényt, hogy a társulat elnöke, Báró Eötvös Loránd 1894 nyarán Magyarország kultuszminisztere lett.
Az első versenyt 1894 szeptember 17-én tartották az abban az évben érettségizett tanulók számára, összesen két helyszínen - a két egyetemi városban -, Budapesten és Kolozsváron. Összesen 29 diák adott be dolgozatot. Az eredményt október 25-én, a Társulat ünnepélyes ülésén hirdették ki, ahol Eötvös, a Társulat elnöke - egyben miniszter és az Akadémia elnöke - személyesen adta át az első és második helyezettnek a díjakat. Ezeket a díjakat már akkor ,,Báró Eötvös-díj''-nak nevezték. Később érem is járt a díjjal, amelyet Eötvös csináltatott. Ma már sajnos egyetlen ilyen érem sem lelhető fel Magyarországon, de megmaradt Eötvös hagyatékában az érem terve. Ennek alapján készíttette el a centenáriumra az Eötvös Loránd Fizikai Társulat azt a díszes oklevelet, amelyet idén először kaptak az Eötvös verseny nyertesei.
1994 október 21-én tizenöt helyszínen: Budapesten, Szegeden, Debrecenben, Pécsett, Miskolcon, Veszprémben, Győrött, Egerben, Nyíregyházán, Békéscsabán, Nagykanizsán, Pakson, Sopronban, Székesfehérváron és Szombathelyen rendezték meg egyidőben a versenyt a szokásos feltételekkel: indulhattak az az évben érettségizettek, valamint középiskolai tanulók. A megoldási idő 300 perc volt, minden segédeszközt (könyveket, jegyzeteket, zsebszámológépet) lehetett használni. Összesen 336 versenyszerű dolgozat érkezett be a feladatokat kitűző és a megoldásokat értékelő Versenybizottsághoz (elnök: Radnai Gyula, tagok: Károlyházy Frigyes, Gnädig Péter).

Ismertetjük a feladatokat, azok megoldását és a verseny eredményét.

1. feladat. Egy tóba

20

m mélyre lesűllyesztett,

1 m^{3}

űrtartalmú búvárharang megtelt vízzel. A felszínen úszó hajóból vékony csövön át levegőt pumpálunk a harang alá. (A harang súlyos, még ekkor sem emelkedik fel.) A levegő és a víz hőmérséklete között nincs számottevő különbség.
| Legalább mekkora munkát végez a kompresszor az

1 m^{3}

víz kiszorítása során?

Károlyházy Frigyes

Megoldás. Készítsünk vázlatos ábrát a folyamatról! Hagyjunk el minden felesleges részletet, hogy maga a termodinamikai folyamat jól látható legyen. Két, egymást követő részfolyamatról van szó:
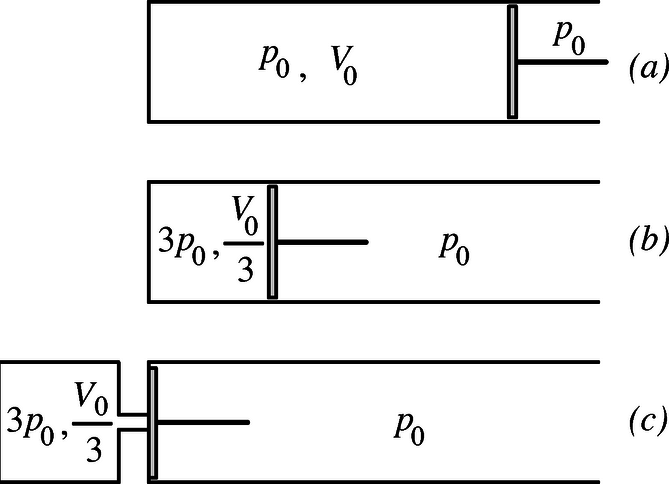
| először össze kell nyomni a gázt a megfelelő nagyobb nyomásra (20 méterrel a víz felszíne alatt a nyomás a légkori nyomásnak kereken háromszorosa);
| ezután a megfelelő nyomású gázt át kell nyomni a búvárharang alá, a víz helyére.
Mindezt az 1. ábrán vázoltuk.
Úgy tűnik, hogy a dugattyút nyomó erő munkáját kell meghatározni. Ez azonban nagyobb, mint a kompresszor által végzett munka, mert ,,besegít'' a külső légnyomás is. Így a kompresszor által végzett munka a 2. ábrán bevonalkázott területtel lesz egyenlő: a dugattyú által végzett összes munkából le kell vonni a légköri nyomás által végzett

p_{0} V_{0}

munkát.
Az izotermikus tágulási munka kiszámítási formája megtalálható a függvénytáblázatban:

\begin{matrix} W = N k T ln \frac{V_{2}}{V_{1}} . \end{matrix}

Esetünkben izoterm összenyomásról van szó, és a külső munkát kell kiszámítanunk. Felhasználva az állapotegyenletet (

p_{0} V_{0} = N k T_{0}

) és azt, hogy a térfogatot harmadrészére kell csökkenteni, az izoterm összenyomáshoz szükséges munka:

\begin{matrix} W_{T} = p_{0} V_{0} ln 3. \end{matrix}

Behelyettesítve

p_{0} \approx 10^{5}

Pa és

V_{0} = 3 m^{3}

értékeket:

\begin{matrix} W_{T} \approx 330 kJ . \end{matrix}

Ehhez kell hozzáadnunk az átnyomáshoz szükséges munkát, amelyet úgy számíthatunk ki, hogy a dugattyút nyomó állandó erőt megszorozzuk a dugattyú elmozdulásával:

\begin{matrix} W_{átnyomási} = F \cdot s = 3 p_{0} A \cdot \frac{V_{0} / 3}{A} = p_{0} V_{0} = 300 kJ . \end{matrix}

Így az összes munka

630

kJ.
Most már csak a külső

p_{0}

nyomás által végzett

p_{0} V_{0}

munkát kell levonnunk, hogy megkapjuk a kompresszorra jutó részt:

\begin{matrix} W_{kompresszor} = 630 kJ - 300 kJ = 330 kJ . \end{matrix}

Ezzel válaszoltunk a feladat kérdésére.

Kiegészítő megjegyzések.
1. Az izoterm munka kiszámítási formulájához úgy lehet eljutni, hogy az izoterma alatti területet határozzuk meg:

\begin{matrix} \begin{matrix} W & = \int_{V_{1}}^{V_{2}} p d V = \int_{V_{1}}^{V_{2}} \frac{N k T}{V} d V = N k T \int_{V_{1}}^{V_{2}} \frac{1}{V} d V, \\ W & = N k T ln \frac{V_{2}}{V_{1}} . \end{matrix} \end{matrix}

2. Vajon nem lehet-e az izotermikus folyamat helyett más folyamattal, kevesebb befektetett munka árán is célhoz érni?
Adiabatikus összenyomáskor kevesebb munka is elég lenne a

3 p_{0}

nyomás eléréséhez. Viszont akkor fel is melegedne a gáz, amely azután az átnyomás közben kezdene lehűlni, s így csökkenne a nyomása. Épp ezért

3 p_{0}

-nál jóval nagyobb nyomásra kellene adiabatikusan összenyomni, ehhez pedig már több munkára lenne szükség, mint az izotermikus esetben.
És ha először lehűtenénk a gázt? Állandó

p_{0}

nyomáson

\frac{T_{0}}{3}

hőmérsékletűre hűtve, a térfogata

\frac{V_{0}}{3}

lenne. Eközben csak a külső légkör végezne munkát. Majd pedig hagynánk a gázt állandó

\frac{V_{0}}{3}

térfogaton visszamelegedni

T_{0}

hőmérsékletre, ekkor a nyomása elérné a

3 p_{0}

értéket, s csak az átnyomási munkát kellene a kompresszorral végeztetni. Lehet, hogy 200 kJ is elég lenne? Ez már ravaszabb gondolat, de azt lehet ellene felhozni, hogy a feladatban szó se volt arról, hogy a hajón még egy megfelelő hűtőberendezés is működik, amelyet felhasználhatunk a probléma megoldásához. De tegyük fel, hogy megengednénk a hűtőgép használatát, akkor viszont azt a munkát is illene számításba venni, amivel a hűtőgépet | pl. a hűtőgép kompresszorát | működtetni kell. Nem lenne nehéz megmutatni, hogy ismét ,,ráfizetünk'': összesen több munkát kell végeznünk.
3. Úgy is ki lehet számítani a kompresszor által végzett munkát, hogy elképzeljük: a kezdetben

3 m^{3}

-nyi levegőt egy ,,zsákba'' zárjuk, és a zsákot lassan lehúzzuk 10 m-nyire a víz alá. Mivel

x

méter mélységben az izotermikusan összenyomott gázra

F (x) = 3 \cdot 10^{4} \cdot {(1 + x / 10)}^{- 1}

felhajtóerő hat, a lehúzás során végzett munka (SI-egységrendszerben számolva)

\begin{matrix} W = \int_{0}^{20} f (x) d x = \int_{0}^{20} \frac{3 \cdot 10^{4}}{1 + x / 10} d x = 3 \cdot 10^{5} \cdot ln 3 \approx 330 kJ . \end{matrix}

2. feladat. Egy henger alakú edény szuperfolyékony héliummal van tele. Az edény magassága

1

dm, belső alapterülete

1 {dm}^{2}

.
A héliumra kellő óvatossággal egy ugyancsak henger alakú,

1

dm magas, de csak

0, 99 {dm}^{2}

alapterületű ,,dugót'' helyezünk, és elengedjük. A dugó sűrűsége a hélium sűrűségével egyenlő.
| Hogyan mozog a dugó?
| Mennyi idő alatt ér le az edény aljára?
Az egész berendezés hőmérséklete

0

K közvetlen közelében van, a folyadék súrlódása és felületi feszültsége figyelmen kívül hagyható.

Gnädig Péter

Megoldás. Amikor elengedjük a dugót (3. ábra), ennek esését az alatta lévő folyadék hirtelen lefékezi bizonyos

v_{0}

sebességre. Ezt a dugó további mozgása során kezdősebességnek fogjuk tekinteni.
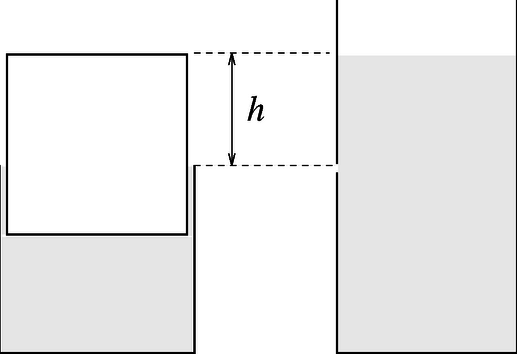
Próbáljuk meg kiszámítani ezt a

v_{0}

kezdősebességet, s csak utána keressük a választ a feladat kérdésére: Hogyan mozog a dugó?
Amint a dugó

v_{0}

sebességgel elindul lefelé, oldalt felspriccel a folyadék. Jelöljük a folyadék kiömlési sebességét

u_{0}

-lal. Ez sokkal nagyobb, mint

v_{0}

, hiszen a folyadék összenyomhatatlansága miatt a

Δ A

területű résen ugyanannyi folyadéknak kell kifreccsennie, mint amennyi az

A

területű dugó alól kiszorul:

\begin{matrix} v_{0} \cdot A = u_{0} \cdot Δ A . \end{matrix}

v_{0}

kiszámításához lehet, hogy először

u_{0}

-t kell meghatároznunk? Ez elég is lenne, hiszen a feladat adataiból az

A : Δ A = 100

arány kiolvasható.
Milyen összefüggésben szerepelhet még a kiömlő folyadék sebessége? Mivel a folyadék súrlódása és felületi feszültsége figyelmen kívül hagyható, ezért érdemes lesz felírni az egész rendszerre a a munkatételt. Eszerint a rendszeren végzett munka a rendszer mozgási energiájának megváltozásával egyenlő.
Munkát végző erő a dugóra ható nehézségi erő. Amíg a dugó | a test |, egy kicsiny

Δ x

-szel elmozdul lefelé, kiszorít

Δ m_{foly}

tömegű folyadékot, amely

u_{0}

sebességgel hagyja el a tartályt. Ezért írhatjuk:

\begin{matrix} m_{test} \cdot g \cdot Δ x = \frac{1}{2} Δ m_{foly} \cdot u_{0}^{2} . \end{matrix}

Igaz, a dugónak is megváltozott a mozgási energiája, de a sokkal kisebb sebesség miatt ezt a folyadék mozgási energiájának változásához képest elhanyagolhatjuk.
Helyettesítsük a fenti egyenletbe a következőket:

\begin{matrix} m_{test} = A l ϱ_{test} és Δ m_{foly} = A Δ x ϱ_{foly} . \end{matrix}

Egyszerűsítés után a következő összefüggés adódik:

\begin{matrix} l ϱ_{test} g = \frac{1}{2} ϱ_{foly} u_{0}^{2} . \end{matrix}

Ez éppen a ,,jó öreg'' Bernoulli-törvény (1738) speciális esete, akár ebből is kiindulhattunk volna

u_{0}

kiszámításához. Ha pedig azt is kihasználjuk, hogy a feladatban most a test és a folyadék sűrűsége egyenlő, a folyadék kiömlési sebességére kapjuk:

\begin{matrix} u_{0} = \sqrt[]{2 g l} . \end{matrix}

Ez a Torricelli-féle kiöntési törvény (1646) még egy évszázaddal korábbról.
Akár át is fogalmazhatjuk a feladatot: Ahelyett, hogy ,,Hogyan mozog a dugó?'', azt kérdezhetjük: ,,Hogyan mozog egy lyukas edényből súrlódásmentesen kiömlő folyadék esetén a folyadék felső szintje?'' Azt már tudjuk, hogyan indul el. Kezdősebessége:

\begin{matrix} v_{0} = \frac{Δ A}{A} u_{0} = \frac{Δ A}{A} \sqrt[]{2 g l} . \end{matrix}

Tekintsünk most egy közbülső esetet a mozgás során. Tegyük fel, hogy a dugónak még

h

magasságú része áll ki a hengerből. A dugó úgy mozog ekkor, mint az oldalt lyukas edényben lévő folyadékok felső szintje abban a pillanatban, amikor ez a szint éppen

h

magasságban van a lyuk felett (4. ábra). Ugyanis mindkét esetben a súrlódásmentesen kiömlő folyadék sebessége

\begin{matrix} u = \sqrt[]{2 g h}, \end{matrix}

és így a dugó sebessége

\begin{matrix} v = \frac{Δ A}{A} u = \frac{Δ A}{A} \sqrt[]{2 g h} . \end{matrix}

Ez még így is írható:

\begin{matrix} v = \sqrt[]{2 {(\frac{Δ A}{A})}^{2} g h}, \end{matrix}

amiből látszik, hogy a dugó mozgása egyenletesen változik, lassulásának nagysága pedig

\begin{matrix} {(\frac{Δ A}{A})}^{2} \cdot g = 10^{- 4} g = 10^{- 3} \frac{m}{s^{2}} . \end{matrix}

A dugó mozgásának sebesség‐idő grafikonja az 5. ábrán látható.
A dugó sebessége éppen akkor csökken egyébként is zérusra, amikor a dugó alja eléri az edény alját, teteje pedig a hengeres edény tetejével kerül egy szintre. (Az analóg példában: a kiömlő folyadék felszíne a lyukhoz ér.)
Így a dugó leérkezéséig eltelt

τ

idő

\begin{matrix} τ = \frac{2 l}{v_{0}} = \frac{2 l}{\frac{Δ A}{A} \sqrt[]{2 g l}} = \frac{A}{Δ A} \sqrt[]{\frac{2 l}{g}} = 14, 1 s . \end{matrix}

Kiegészítő megjegyzések.
1. A leérkezési idő kiszámításakor elhanyagoltuk azt az időtartamot, amennyi idő alatt a dugó felveszi a kezdősebességet, s azt az utat is, amit ez alatt megtesz. Az elhanyagolás jogosságát a következő becsléssel ellenőrzihetjük. A dugó valódi kezdősebessége nulla, de ebből az állapotából | feltételezésünk szerint igen hamar | felgyorsul a kérdéses

v_{0}

sebességre. Amikor elengedjük, a dugó tetején és az aljánál egyaránt a légköri nyomás hat rá, tehát a dugó kezdeti gyorsulása

g

(szabadesés!). Ez a gyorsulás bizonyos

τ_{0}

idő alatt gyarkorlatilag nullára (

10^{- 4} g

-re) csökken, s a dugó sebessége

v_{0}

lesz. Ha átlagosan

g / 2

értékkel számolunk, a

(g / 2) τ_{0} = v_{0}

összefüggésekből

τ_{0} = 2 v_{0} / g = 2 \cdot \frac{Δ A}{A} \sqrt[]{\frac{2 l}{g}} \approx 0, 003 s

adódik. Ez ez idő és a dugó által ezalatt megtett kb.

v_{0} τ_{0} / 2 = 0, 02

mm út valóban elhanyagolható.
2. A szuperfolyékony héliumnak semmi más különleges extrém tulajdonságát | például, hogy lassan magától is kimászna az edényből | nem használtuk ki azon az egyen kívül, hogy nincs belső súrlódása. Éppen elég meglepő ez is!

3. feladat. Függőleges földelt fémsíktól

d

távolságra felfüggesztünk egy

l

hosszúságú fonálingát. Miután az

m

tömegű, kicsiny ingatestet elektromosan feltöltöttük, az inga újra egyensúlyi helyzetet vett fel, s most

α

szöget zár be a függőlegessel (6. ábra).
| Mekkora az ingatest töltése?
| Mennyivel kell közelebb vinnünk a fémsíkot az inga felfüggesztési pontjához, ha azt akarjuk, hogy a függőleges fémsík magához rántsa az ingát?
| Anélkül, hogy közelebb vinnénk, tudjuk-e úgy mozgatni a mindig függőleges fémsíkot, hogy hozzácsapódjon az inga?
A fonál szigetelő, a levegő hatása elhanyagolható, s a feladatot az alábbi numerikus értékek esetén oldjuk meg:

d = 0, 5

l = 4

m = 10^{- 3}

kg;

α = 1^{\circ}

Radnai Gyula

Megoldás. Tisztázzuk először a fémsík szerepét! Tudjuk, hogy elektrosztatikus esetben a fémek felülete mindig ekvipotenciális. (Addig-addig mozognak, rendeződnek rajtuk a töltések, amíg ez az állapot ki nem alakul.) Ez azt jelenti, hogy a fémek felületénél az elektromos térerősségnek nem lehet érintő irányú komponense, vagyis a térerősség minden pontban merőleges a fém felületére. A feladatban ponttöltés és sík fémfelület szerepel, ezért az erőtérnek a 7(a) ábrán vázolt szerkezetűnek kell lennie. Ezzel az erőtérrel ekvivalens egy olyan dipólus erőterének ,,egyik fele'', amelyet egymástól

2 x

távolságra lévő

Q

és

- Q

ponttöltések hoznak létre, ahogyan azt a 7(b) ábrán vázoltuk.
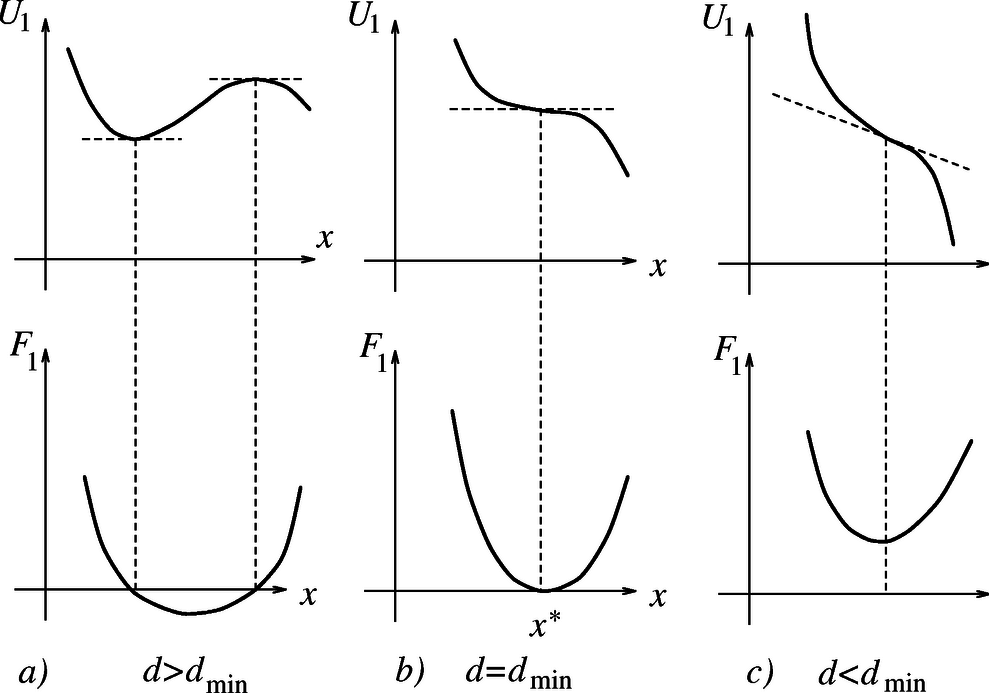
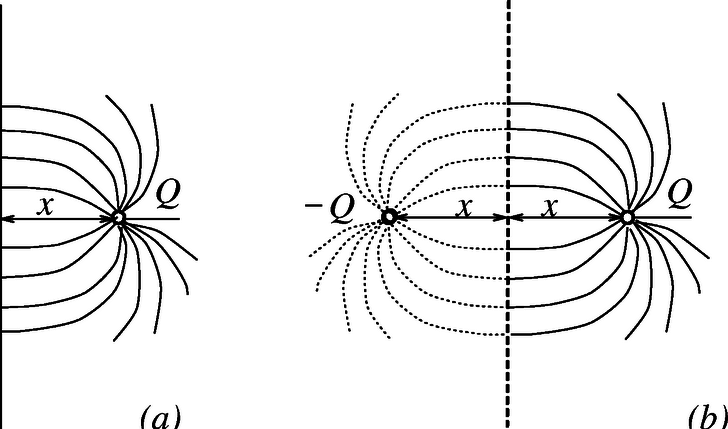
A fémsík hatása tehát minden tekintetben helyettesíthető egy

- Q

nagyságú ú.n. ,,tükörtöltés'' hatásával. Ennek a felismerésnek köszönhetően azt az erőt, amit a fémsík fejt ki a

Q

tötésre, úgy is kiszámíthatjuk, mint a tükörtöltés által kifejtett vonzóerőt.
A Coulomb-erőn kívül a

Q

töltésre még két erő hat (8. ábra): a nehézségi erő és a fonálerő. A három erő eredője akkor zérus | akkor van egyensúly |, ha a Coulomb-erő és a nehézségi erő hányadosa

tg α

-val egyenlő. Ebből határozhatjuk meg a

Q

töltés keresett értékét.

\begin{matrix} m g tg α = k \frac{Q^{2}}{{[2 (d - l sin α)]}^{2}} . \end{matrix}

Átrendezés után:

\begin{matrix} Q = 2 (d - l sin α) \sqrt[]{\frac{m g}{k} tg α}, \end{matrix}

(

k = 9 \cdot 10^{9} \frac{N m^{2}}{C^{2}}

g = 9, 81 \frac{m}{s^{2}}

, a többi paraméter értéke a feladatban adott). Behelyettesítések után kapjuk:

\begin{matrix} Q = 1, 187 \cdot 10^{- 7} C . \end{matrix}

Mi történik, ha a fémsíkot közelebb visszük az ingához? A Coulomb-erő nő, mivel a tükörtöltéstől való távolság csökken. A nehézségi erő nem változik, tehát egy nagyobb

α

szög esetén tud újra beállni az egyensúly. De van-e ilyen új

α

szög? Hiszen az inga kilendülésével a Coulomb-erő tovább nő, és lehet, hogy az inga meg se áll addig, amíg hozzá nem csapódik a fémsíkhoz.
Meg kell határoznunk azt az összefüggést, amely egyensúly esetén fennáll

d

és

α

között. Formálisan tekintsük

d

-t

α

függvényének, s fejezzük ki ezt a függvényt az egyensúlyra már felírt fenti összefüggésből. Ezt kapjuk:

\begin{matrix} d = d (α) = l sin α + \sqrt[]{\frac{k Q^{2}}{4 m g}} \frac{1}{\sqrt[]{tg α}} . \end{matrix}

A függvény menete viszonylag kis

α

értékek környezetében a 9. ábrán látható módon egy minimumot mutat. Van tehát egy olyan legkisebb

d

érték, amelynél közelebb nem vihetjük a fémsíkot. Ha közelebb visszük, nincs egyensúlyi állapot, tehát hozzácsapódik az inga a fémsíkhoz.
Határozzuk meg

d

minimumát!
(Akiknek gondot okoz e kissé bonyolult függvény differenciálása, úgy segíthetnek magukon, ha | felismerve, hogy csak kis szögekröl van szó |,

sin α

és

tg α

helyére

α

-t írnak. Ekkor csak hatványfüggvényeket kell deriválni, s a végeredmény legfeljebb a negyedik‐ötödik értékes jegyben tér el a pontos eredménytől.)
A minimum helyére (

α^{*}

) kapjuk:

\begin{matrix} sin 2 α^{*} (\approx 2 α^{*}) = \sqrt[3]{\frac{k Q^{2}}{2 m g l^{2}}}, ebből α^{*} = 2, 12^{\circ}, \end{matrix}

d

legkisebb lehetséges értékére pedig ez adódik:

\begin{matrix} d_{{min}_{}^{}} = 0, 4435 m = 44, 35 cm . \end{matrix}

Mivel a fémsík eredetileg

0, 5

méterre volt az inga felfüggesztési pontjától, ezért ahhoz, hogy a fémsík magához rántsa az ingát, legalább

Δ d = 5, 65 cm

-rel közelebb kell vinni.
Már csak arra kell válaszolnunk, hogy tudjuk-e úgy mozgatni a fél méterre lévő fémsíkot, hogy hozzácsapódjon az inga akkor is, ha sohasem kerül a fémsík fél méternél közelebb a felfüggesztési ponthoz.
Igen, tudjuk: ,,be kell lengetni az ingát'', mint egy hintát. Elöször eltávolítjuk a fémsíkot, ekkor az inga hátralendül. Amikor az inga elindul visszafelé, visszahozzuk a fémsíkot, hogy vonzóerejével növelje a lengés amplitúdóját. Lényegében az inga lengésével szinkronban, de mindig ellentétes fázisban kell mozgatni a fémsíkot. Akármilyen kis amplitúdóval is rezegtetjük a fémsíkot, ha ez megfelelő fázisban történik, előbb-utóbb hozzácsapódik az inga.

Kiegészítő megjegyzések.
1. Tanulságos áttekinteni a feladat energetikai megoldását is. Nemcsak azért, mert ez egy második megoldás, hanem azért is, mert olyan új felismeréshez vezet, amely az előző megoldásból nem derült ki.
A fémsíkon influált (elektromosan megosztott) töltésrendszer potenciális energiájának felírása elég bonyolult feladat, ezért ismét alkalmazzuk a tükörtöltéses módszert. Az inga + fémsík rendszer helyett tekintsük az inga + tükörképinga rendszert (10. ábra), és írjuk fel e két ingából álló rendszer öszes potenciális energiáját! Ez a két ingatest gravitációs helyzeti energiáiból és az elektrosztatikus kölcsönhatási energiáiból tevődik össze (az utóbbi negatív).

\begin{matrix} U = m g (l - l cos α) + m g (l - l cos α) - k \frac{Q^{2}}{2 (d - l sin α)} . \end{matrix}

Egyetlen inga potenciális energiája ennek a fele lesz:

\begin{matrix} U_{1} = m g (l - l cos α) - k \frac{Q^{2}}{4 (d - l sin α)} . \end{matrix}

Az egyszerűség kedvéért foglalkozzunk most is a kis szögek esetével, legyen

\begin{matrix} \begin{matrix} x = l sin α \approx k α, és h = l - l cos α \approx l \frac{α^{2}}{2} . \\ Ezzel U_{1} (α) = \frac{m g}{2} l α^{2} - k \frac{Q^{2}}{4} \frac{1}{d - l α}, \\ vagy áttérve azx = l αváltozóra: U_{1} (x) = \frac{m g}{2 l} x^{2} - \frac{k Q^{2}}{4} \frac{1}{d - x} . \end{matrix} \end{matrix}

Ezt az

U_{1} (x)

függvényt

x

szerint differenciálva kapjuk meg az ingatestre ható (

x

irányú) erő

- 1

-szeresét, tehát az erő:

\begin{matrix} F_{1} (x) = - \frac{d U_{1} (x)}{d x} = \frac{m g}{l} x - \frac{k Q^{2}}{4} \frac{1}{{(d - x)}^{2}} . \end{matrix}

Mind az

U_{1} (x)

, mind az

F_{1} (x)

függvények menete a paraméterek értékeitől függ. Ha

m

g

l

k

Q

állandó, akkor egyedül

d

-től. A 11. ábrán vázoltunk három különböző esetet. Az a) esetben a potenciális energia minimuma jelöli ki az inga stabilis egyensúlyi helyzetét, a maximum egy labilis egyensúlyt jelez. A c) esetben nincs egyensúlyi helyzet. A kettő közti átmenetet, a határesetet mutatja az ábra b) része, amikor a potenciális energiának ,,vízszintes'' érintőjű inflexiós pontja van, itt valósulhat meg még utoljára egyensúlyi helyzet. Az ehhez tartozó

d

paraméterérték lesz

d

legkisebb értéke.

x = x^{*}

helyen tehát

\frac{d U_{1}}{d x} = 0

és

\frac{d F_{1}}{d x} = 0

is igaz.
Ebből a két feltevésből az alábbi egyenletekre jutunk:

\begin{matrix} 2 x {(d - x)}^{2} = \frac{k Q^{2} l}{2 m g}, illetve {(d - x)}^{3} = \frac{k Q^{2} l}{2 m g} . \end{matrix}

Ezek szerint

2 x = d - x

, vagyis

x = \frac{d}{3}

a határesetben!
A fenti jelölésekkel:

x^{*} = \frac{d_{{min}_{}^{}}}{3}

.
Ez az a szép és érdekes eredmény, ami nem jött ki az első megoldás során: a fémsík egészen addig közelíthető az ingához, amíg az inga kilendüléséhez tartozó

x

érték el nem éri az éppen akkori

d

távolság harmadrészét. Ha elérte, s még tovább közelítjük a fémsíkot, akkor már nekicsapódik az inga.
Természetesen a feltételi egyenletek bármelyikébe behelyettesítve

x = \frac{d}{3}

értékét, megkapjuk

d = d_{{min}_{}^{}}

értékét:

\begin{matrix} d = d_{{min}_{}^{}} = \frac{3}{2} \sqrt[3]{\frac{k Q^{2} l}{2 m g}} = 0, 4435 m \end{matrix}

2. A feladat harmadik kérdésére a ,,belengetésen'' kívül más ötletes válaszok, megoldási javaslatok is születtek. Ilyen például a fémsík körbeforgatása, amely körmozgásra csábítja az ingatestet. Voltak, akik a fémsík saját síkjában történő mozgatással próbálkoztak, számítva az elektronok tehetetlenségére, s a mozgó töltésekre ható Lorentz erővel is többen próbálkoztak | nem sok sikerrel. Elág sok jó fizikai szemléletű versenyző akadt, aki | ha nem is tudta megoldani a feladat nehéz, középső részét |, erre a befejező kérdésre jól válaszolt.

A verseny eredménye

Megosztott I‐II. díjat nyert egyenlő helyezésben a következő három versenyző:
Horváth Péter, a Fazekas Mihály Fővárosi Gyakorló Gimnázium IV. osztályos tanulója (felső fénykép), Horváth Gábor tanítványa;
Kovács Krisztián, a békéscsabai Kemény Gábor Műszaki Szakközépiskola IV. osztályos tanulója (középső fénykép), Mekis László és Varga István tanítványa;

Varga Dezső, a miskolci Földes Ferenc Gimnázium IV. osztályos tanulója (alsó fénykép), id. Szabó Kálmán tanítványa.
III. díjat nyert egyenlő helyezésben a következő hét versenyző:
Borsányi Szabolcs, a budapesti Piarista Gimnázium IV. osztályos tanulója, Görbe László tanítványa;
Burcsi Péter, a pápai Türr István Gimnázium III. osztályos tanulója, Németh Zsolt tanítványa;
Futó Gábor, az ELTE TTK matematikus szakos hallgatója, aki a Fazekas Mihály Fővárosi Gyakorló Gimnáziumban érettségizett, mint Horváth Gábor tanítványa;
Juhász Sándor, a Fazekas Mihály Fővárosi Gyakorló Gimnázium IV. osztályos tanulója, Horváth Gábor tanítványa;
Koblinger Egmont, a Fazekas Mihály Fővárosi Gyakorló Gimnázium IV. osztályos tanulója, Horváth Gábor tanítványa;
Mizera Ferenc, az ELTE TTK fizikus szakos hallgatója, aki Szlovákiában, Rév-Komáromban érettségizett, mint Szakál Ildikó, Spátai Lotár és Szabó Endre tanítványa;
Tóth Gábor Zsolt, a budapesti Árpád Gimnázium III. osztályos tanulója, Vankó Péter tanítványa.
Dicséretben részesültek, s erről oklevelet kaptak a verseny 11‐15. helyezettjei:
11. Halbritter András, a BME mérnök‐fizikus szakos hallgatója, aki a győri Czuczor Gergely Bencés Gimnáziumban érettségizett, mint Csonka László tanítványa; 12‐13. Bárász Mihály, a Fazekas Mihály Fővárosi Gyakorló Gimnázium III. osztályos tanulója, Horváth Gábor tanítványa; Várhegyi Péter, a BME mérnök‐fizikus szakos hallgatója, aki a Fazekas Mihály Fővárosi Gyakorló Gimnáziumban érettségizett, mint Horváth Gábor tanítványa; 14‐15. Koncz Imre, a Fazekas Mihály Fővárosi Gyakorló Gimnázium II. osztályos tanulója, Horváth Gábor tanítványa; Lovas Rezső, a debreceni KLTE Gyakorló Gimnáziumának III. osztályos tanulója, Dudics Pál, Kirsch Éva és Szegedi Ervin tanítványa.
Jegyzőkönyvi dicséretben részesültek a 16‐20. helyezett versenyzők egyenlő helyezésben:
Feldmann Márton, a soproni Vas- és Villamosipari Szakközépiskola IV. osztályos tanulója, Lendvay Péterné tanítványa; Juhász Bertalan, a debreceni KLTE Gyakorló Gimnáziumának IV. osztályos tanulója, Dudics Pál tanítványa; Madarassy Pál, a ELTE TTK térképész szakos hallgatója, aki a Fazekas Mihály Fővárosi Gyakorló Gimnáziumban érettségizett, mint Horváth Gábor tanítványa; Radnóti Gergely, a paksi Vak Bottyán Gimnázium IV. osztályos tanulója, Horváthné Szabó Julianna és Gálosiné Kimle Mária tanítványa; Salk Miklós, a pécsi Babits Mihály Gimnázium IV. osztályos tanulója, Koncz Károly tanítványa.
Gratulálunk a nyerteseknek!

Radnai Gyula