Kezdőlap


Cím:	A feszültségi rezonanciáról
Szerző(k):	Légrádi Imre
Füzet:	1995/január, 44 - 47. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek
Hivatkozás(ok):	Feladatok: 1995/január: 2860. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az ideális soros $R L C$ kör vizsgálata során több tankönyvben találkozhatunk a következő gondolattal:
,,Ha a kapacitív és induktív ellenállás értéke megegyezik, akkor a fáziseltolódás szöge nulla, és adott kapocsfeszültség esetén maximális áram folyik át az $R L C$ körön. Ennek következtében az egyes kapcsolási elemeken maximális feszültség jelenik meg. Ezt az esetet feszültségi rezonanciának nevezzük.''
Az alábbiakban arra szeretnék rámutatni, hogy ezt az esetet nem helyes feszültségi rezonanciának nevezni, mert a feszültség maximuma nem ekkor következik be.

1. ábra

Tekintsük az ideális elemekből felépített soros

R L C

kört, amin azt értjük, hogy

R

-ben koncentráltuk az összes ohmos ellenállást,

L

tiszta induktív ellenállás, és

C

tiszta kapacitív ellenállás. A kapcsolás (1. ábra) közismert. Kapcsoljuk az

R L C

kört színuszos változóáramú áramforrásra, amelynek

ω

körfrekvenciáját folyamatosan lehet változtatni. Legyen a kapocsfeszültség mindenkor állandó

U_{0}

érték. Mint tudjuk, ilyenkor az impedancia abszolút értéke

\begin{matrix} Z = \sqrt[]{R^{2} + {(\frac{1}{ω C} - ω L)}^{2}} . \end{matrix}

Az áramkörben folyó áram erőssége

I = U_{0} / Z

. Ennek az áramnak az

ω

körfrekvencia függvényében akkor van maximuma, amikor

X_{0} = X_{L}

, azaz amikor

ω_{0} = 1 / \sqrt[]{L C}

. Az ennek megfelelő frekvenciát valóban nevezhetjük rezonanciafrekvenciának. Mivel ilyenkor nemcsak az a fontos jelenség áll elő, hogy az áram értéke maximális, hanem az is, hogy az áram éppen azonos fázisban van a kapocsfeszültséggel, vagyis a fáziseltolódás értéke nulla; ezért az elektrotechnika ezt az esetet fázisrezonanciának nevezi.
A későbbi egyszerű és szemléletes tárgyalás érdekében itt hívom fel a figyelmet arra, hogy az áramerősség görbéjét az

ω

körfrekvencia függvényében felrajzolva, a fázisrezonancia helyén nyilván azt láthatjuk, hogy a görbe érintője ezen a helyen ,,vízszintes''.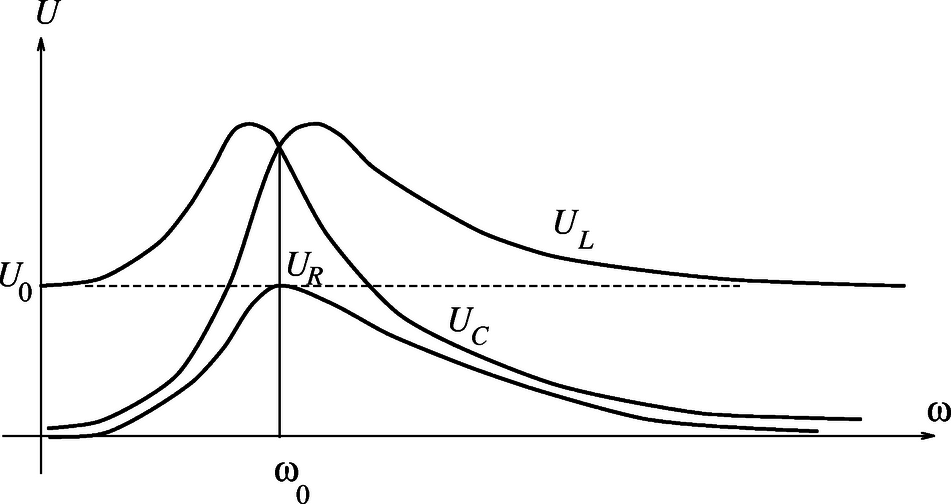

2. ábra

Nézzük a kondenzátorra eső feszültség függését a körfrekvenciától. Ez Ohm törvénye szerint:

U_{C} = I \cdot X_{C} = I \cdot (1 / ω C)

. Nyilván, ha

ω = 0

, azaz egyenáram esetén,

U_{C} = U_{0}

. Ha ezután a körfrekvenciát folyamatosan növeljük, és a kondenzátor sarkain mérhető

U_{C}

feszültséget

ω

függvényében ábrázoljuk, akkor

U_{C}

-nek az előbbi

U_{0}

értékből kiindulva folytonos, sima görbét kell adnia. Ha ezt a görbét az áramerősség maximumához tartozó rezonancia-körfrekvencia környezetében vizsgáljuk, akkor azt állapíthatjuk meg, hogy a görbe az

ω_{0} = 1 / \sqrt[]{L C}

helyen ,,ereszkedően'' halad át. Hogy ez így van, azt a következőképpen láthatjuk be:

U_{C} = I \cdot (1 / ω C)

. Ez egy kéttényezős szorzat. Az első tényező az áramerősség. Mint már említettük, a szóban forgó helyen

I

görbéjének érintője vízszintes, vagyis azt mondhatjuk, hogy kis körfrekvenciaváltozást tekintve e hely környezetében az áramerősség állandó. A második tényező a kondenzátor váltóáramú ellenállása, amely

ω

növekedésével csökken. Ha tehát az áramerősség maximumához tartozó körfrekvenciánál kicsit kisebb frekvenciától haladunk a nála nagyobb frekvenciák felé, akkor

U_{C}

-t úgy számíthatjuk ki, hogy állandó áramerősséget szorzunk csökkenő ellenállással, amely szorzás eredménye csökkenő feszültség kell legyen.
Ha tehát a

0

‐

ω_{0}

körfrekvencia intervallumban van maximális

U_{C}

érték, akkor annak

ω_{0}

-nál kisebb körfrekvenciánál kell lennie. Más szavakkal, a kondenzátoron mérhető legnagyobb feszültség nem

ω_{0}

-nál, hanem annál kisebb körfrekvenciánál van! Vagyis a feszültségrezonancia nem

ω_{0}

-nál van!
Keressük meg, mekkora

ω

körfrekvenciánál van a feszültségnek maximuma. Minthogy

\begin{matrix} U_{C} = I \cdot X_{C} = \frac{U_{0}}{Z} \cdot X_{C} = \frac{U_{0} \cdot \frac{1}{ω C}}{\sqrt[]{R^{2} + {(\frac{1}{ω C} - ω L)}^{2}}} = \frac{U_{0}}{C \sqrt[]{R^{2} ω^{2} + {(\frac{1}{ω C} - ω L)}^{2} ω^{2}}} . \end{matrix}

Látható, hogy

U_{C}

-nek annál a körfrekvenciánál van maximuma, amely körfrekvenciánál a nevezőnek minimuma van, vagyis elég a gyök alatti mennyiséget vizsgálni minimum tekintetében.
A gyök alatti mennyiség

ω^{2} = x

-ben másodfokú kifejezéssé alakítható:

\begin{matrix} \begin{matrix} R^{2} ω^{2} + {(\frac{1}{ω C} - ω L)}^{2} ω^{2} = R^{2} ω^{2} + (\frac{1}{ω^{2} C^{2}} - \frac{2 L}{C} + ω^{2} L^{2}) ω^{2} = \\ = L^{2} ω^{4} + (R^{2} - \frac{2 L}{C}) ω^{2} + \frac{1}{C^{2}} = L^{2} x^{2} + (R^{2} - \frac{2 L}{C}) x + \frac{1}{C^{2}} . \end{matrix} \end{matrix}

A kapott kifejezésben a másodfokú tag együtthatója pozitív, tehát a kifejezésnek létezik minimuma, mégpedig a másodfokú függvények vizsgálatából jól ismert ,,

- b / 2 a

'' helyen, vagyis a minimum helyére vonatkozólag fennáll:

\begin{matrix} ω^{2} = \frac{\frac{2 L}{C} - R^{2}}{2 L^{2}} = \frac{1}{L C} - \frac{R^{2}}{2 L^{2}}, azaz ω = \sqrt[]{\frac{1}{L C} - \frac{R^{2}}{2 L^{2}}} < ω_{0} . \end{matrix}

Természetesen ehhez az eredményhez deriválással is eljuthatunk.
Szemléltetésképpen vegyünk fel számadatokat is. Legyen

L = 10

henry,

C = 5 μ F

és

R = 1000

ohm. Ebben az esetben a kondenzátoron mérhető feszültség maximumához tartozó körfrekvencia

ω = 122, 5 s^{- 1}

, amely valóban kisebb

ω_{0} = 141, 4 s^{- 1}

-nél.
Vizsgáljuk meg azt is, hogy az ideális tekercsen mérhető feszültségnek hol van maximuma. Jelöljük

U_{L}

-lel a tekercsen lévő feszültséget, akkor, mint fentebb is, írhatjuk, hogy

\begin{matrix} U_{L} = I \cdot X_{L} = \frac{U_{0} \cdot ω L}{\sqrt[]{R^{2} + {(\frac{1}{ω C} - ω L)}^{2}}} = \frac{U_{0} \cdot L}{\sqrt[]{\frac{R^{2}}{ω^{2}} + {(\frac{1}{ω C} - ω L)}^{2} \cdot \frac{1}{ω^{2}}}} . \end{matrix}

Ismét láthatjuk, hogy

U_{L}

-nek annál az

ω

-nál van maximuma, amelynél a nevezőben lévő gyök alatti mennyiségnek minimuma van. A gyök alatti mennyiséget átírhatjuk egy másodfokú függvény formájába, amelyben a változó

1 / ω^{2} = x

\begin{matrix} \begin{matrix} \frac{R^{2}}{ω^{2}} + {(\frac{1}{ω C} - ω L)}^{2} \cdot \frac{1}{ω^{2}} = \frac{R^{2}}{ω^{2}} + (\frac{1}{ω^{2} C^{2}} - \frac{2 L}{C} + ω^{2} L^{2}) \cdot \frac{1}{ω^{2}} = \\ = \frac{1}{C^{2}} {(\frac{1}{ω^{2}})}^{2} + (R^{2} - \frac{2 L}{C}) \cdot \frac{1}{ω^{2}} + L^{2} = \frac{1}{C^{2}} x^{2} + (R^{2} - \frac{2 L}{C}) x + L^{2} . \end{matrix} \end{matrix}

A kapott másodfokú függvényben a másodfokú tag együtthatója pozitív, tehát a függvénynek létezik minimuma, amelynek helye az előbbiekhez hasonlóan ,,

- b / 2 a

''. Ennek megfelelően

\begin{matrix} \frac{1}{ω^{2}} = \frac{2 L C - R^{2} C^{2}}{2}, ω^{2} = \frac{2}{2 L C - R^{2} C^{2}}, ω = \sqrt[]{\frac{2}{2 L C - R^{2} C^{2}}} > ω_{0} . \end{matrix}

Természetesen ezt az eredményt is megkaphatnánk deriválás segítségével.
Az előzőekben felvett numerikus adatokkal most

ω = 163, 3 s^{- 1}

-et kapunk arra a körfrekvenciára, amelynél az ideális tekercsen mérhető feszültség a legnagyobb. Látható, hogy ez nagyobb

ω_{0}

-nál, aminek magyarázata a kondenzátornál elmondottakhoz hasonlóan adható meg:

U_{L} = I \cdot X_{L} = I \cdot ω L

. Minthogy

ω_{0}

környezetében

I

állandónak tekinthető,

X_{L}

viszont a kisebb körfrekvenciáktól a nagyobbak felé haladva növekszik, ezért a két tényező szorzata is növekszik

ω_{0}

környezetében.

U_{L}

görbéje tehát ,,emelkedőleg'' halad át

ω_{0}

helyen, viszont igen nagy körfrekvenciánál vissza kell térnie

U_{0}

érték közelébe, hiszen igen nagy frekvencián a kondenzátor ellenállása zérushoz tart, a tekercsé viszont igen nagy lesz az ohmos ellenálláséhoz képest, így jóformán az egész

U_{0}

a tekercsre esik. Ha tehát

U_{L}

valahol maximális értékű, akkor az csak

ω_{0}

-nál nagyobb körfrekvencián lehet.
Azt mondhatjuk tehát, hogy az ideális elemekből álló soros

R L C

körben a feszültségrezonancia nem

ω_{0} = 1 / \sqrt[]{L C}

körfrekvenciánál következik be, hanem a kondenzátoron

ω_{0}

-nál kisebb, a tekercsen pedig

ω_{0}

-nál nagyobb körfrekvencián.

Érdekes felfigyelni még a következőkre.
Először a numerikus adatokkal kapott körfrekvenciákat vizsgálva képezzük a két feszültségrezonanciához tartozó körfrekvencia mértani középarányosát:

\begin{matrix} \sqrt[]{122, 5 \cdot 163, 3} = 141, 4. \end{matrix}

Ez utóbbi viszont

ω_{0}

-nak tűnik!
Ezen intuíció alapján kimondjuk a következő tételt: A soros

R L C

körben a kondenzátor feszültségrezonanciájához tartozó körfrekvenciának és a tekercs feszültségrezonanciájához tartozó körfrekvenciának a mértani középarányosa a fázisrezonanciához tartozó körfrekvencia.
Bizonyítás: A két előbb kapott körfrekvenciaképlet közvetlen felhasználásával:

\begin{matrix} \begin{matrix} {(\sqrt[]{\frac{1}{L C} - \frac{R^{2}}{2 L^{2}}} \cdot \sqrt[]{\frac{2}{2 L C - R^{2} C^{2}}})}^{\frac{1}{2}} = \\ = {(\sqrt[]{\frac{2 L - R^{2} C}{2 L^{2} C} \cdot \frac{2}{(2 L - R^{2} C) \cdot C}})}^{\frac{1}{2}} = \frac{1}{\sqrt[]{L C}} = ω_{0} . \end{matrix} \end{matrix}

Légrádi Imre