Kezdőlap


Cím:	Az 1994-95. évi OKTV feladatai és eredménye
Füzet:	1995/november, 463 - 470. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az elmúlt tanév Arany Dániel Matematika Verseny és az Országos Középiskolai Tanulmányi Verseny matematika feladatait és eredményeit az Országos Közoktatási és Szolgáltató Intézet kiadványából vettük át, amelyben a példák megoldásai is megtalálhatók. Ez segítséget nyújthat az e tanévi versenyekre való felkészülésben is!
A kiadvány megrendelhető: OKSZI, 1054 Budapest, Báthori u. 10.
Levélcím: 1399 Budapest, Pf. 701/432.

I. Kategória
(A szakközépiskolák tanulói)

Első (iskolai) forduló

1. Oldja meg a következő egyenletrendszert a valós számok halmazán:

\begin{matrix} \begin{matrix} x + y & = 1; \\ x^{5} + y^{5} & = 31. \end{matrix} \end{matrix}

2. Határozza meg azokat az

(x; y)

valós számpárokat, amelyek eleget tesznek a következő feltételek mindegyikének:

*	a)az $x$ egész szám;

*	b) $x^{2} + y^{2} \leq 90$ ;

*	c) $2 x^{2} - x y + 10 = 0$ .

3. Adott egy konvex hatszög, amelynek csúcsai

A

B

C

D

E

F

. Legyen
az

A B C

háromszög súlypontja

B_{1}

, a

B C D

háromszög súlypontja

C_{1}

, a

C D E

háromszög súlypontja

D_{1}

, a

D E F

háromszög súlypontja

E_{1}

, az

E F A

háromszög súlypontja

F_{1}

, az

F A B

háromszög súlypontja

A_{1}

.
Bizonyítsuk be, hogy az

A_{1} B_{1} C_{1} D_{1} E_{1} F_{1}

hatszög középpontosan szimmetrikus!

4. Oldja meg a valós számok halmazán a következő egyenletet:

\begin{matrix} 8^{[\frac{4 x + 1}{5}]} = 2^{7 x - 1} . \end{matrix}

(

[a]

jelenti az

a

valós szám egészrészét.)

5. Igazolja, hogy ha négy egymás után következő

5

-nél nagyobb egész szám egyike sem osztható

5

-tel, akkor a szorzatuk utolsó három számjegye független a négy szám kiválasztásától.

6. Legyenek

a

b

és

c

egy háromszög oldalai és

α

β

γ

rendre a velük szemközti szögek. Bizonyítsuk be, hogy ha

3 α + 2 β = 180^{\circ}

, akkor

a^{2} + b c - c^{2} = 0

Második forduló

1. Legyen

x + \frac{1}{x} = 3

. Igazolja, hogy ekkor

x^{7} + \frac{1}{x^{7}}

egész szám!

2. Oldja meg a pozitív egész számok halmazán az

\begin{matrix} (x + y) z = x y (z - 1) \end{matrix}

egyenletet!

3. Az

A B C

háromszög

B C

oldalának belső pontja legyen

D

. A

D

ponton át húzzunk párhuzamost az

A C

és az

A B

oldalegyenessel. Az előbbi egyenes az

A B

oldalt

E

, az utóbbi egyenes az

A C

oldalt

F

pontban metszi. A

C E

és a

B F

egyenesek metszéspontját jelöljük

G

-vel. Igazolja, hogy az

A E G F

négyszög területe egyenlő a

B C G

háromszög területével!

4. Oldja meg a pozitív számok halmazán az

\begin{matrix} x^{2 sin x - cos 2 x} < \frac{1}{x} \end{matrix}

egyenlőtlenséget!

5. Jelöljük az

A B C

hegyesszögű, nem egyenlő szárú háromszög oldalainak hosszát

a

-val,

b

-vel,

c

-vel, a magasságpontját

M

-mel, a súlypontját

S

-sel! Igazolja, hogy az

M S

egyenes akkor és csakis akkor párhuzamos a

B C

oldallal, ha

\begin{matrix} {(b^{2} - c^{2})}^{2} = a^{2} (2 a^{2} - b^{2} - c^{2}) . \end{matrix}

Harmadik (döntő) forduló

1. Oldja meg a valós számok halmazán a következő egyenletrendszert:

\begin{matrix} \begin{matrix} x - 11 x^{2} & = 11 y - 8 y^{2}; & (1) \\ 6 x + 12 x^{2} & = y + 4 y^{2} . & (2) \end{matrix} \end{matrix}

2. Az

A B C

háromszög

a

b

c

hosszúságú oldalait az ábrán látható módon meghosszabbítottuk. Így a

K L M N P R

hatszöget kaptuk. A hatszög területét

T

-vel, a háromszög területét

t

-vel jelölve, igazolja, hogy

\begin{matrix} T \geq 13 t . \end{matrix}

3. Egy

O

középpontú,

r

sugarú kör

O A

sugarának felezőpontja

F

F

-ben az

O A

sugárra merőleges félegyenest állítunk. Ez az adott kört

K

-ban metszi. Legyen

0^{\circ} < α < 180^{\circ}

, és

E_{1}

és

E_{2}

a kör két olyan (különböző) pontja, amelyekre

E_{1} F K ∢ = K F E_{2} ∢ = α / 2

.
Jelöljük

P

-vel az

O A

és az

E_{1} E_{2}

egyenesek közös pontját. Bizonyítsa be, hogy minden

α

esetén ugyanazt a

P

pontot kapja.
Mit mondhat

P

-ről, ha

α = 180^{\circ}

, illetve ha

180^{\circ} < α < 360^{\circ}

II. Kategória
(Nem speciális matematika tantervű gimnáziumi tanulók)

Első (iskolai) forduló

1. Oldjuk meg az

\begin{matrix} \frac{1}{x} + \frac{1}{y} + z = \frac{5}{2} \end{matrix}

egyenletet, ahol

x

y

z

nem negatív egész számok.

2. Oldjuk meg a valós számok halmazán a következő egyenletet:

\begin{matrix} \sqrt[]{x + 2 \sqrt[]{x - 1}} + \sqrt[]{x - 2 \sqrt[]{x - 1}} = 2 - y^{2} . \end{matrix}

3. Az

A B C

hegyesszögű háromszög

B

és

C

csúcsán átmenő kör az

A B

oldalt

P

-ben, az

A C

oldalt

Q

-ban metszi. Bizonyítsuk be, hogy az

A

csúcsot az

A P Q

háromszög köré írt körének középpontjával összekötő egyenes merőleges

B C

-re.

4. Határozzuk meg az

a_{0}

a_{1}

a_{2}

...

a_{n}

...

sorozat

a_{1995}

elemét, ha

a_{0} = a

adott pozitív egész, és

\begin{matrix} a_{n} = \frac{a_{n - 1} \sqrt[]{3} + 1}{\sqrt[]{3} - a_{n - 1}} (n = 1, 2, ...) . \end{matrix}

5. Igazoljuk, hogy ha

n > 0

egész szám, akkor az

\begin{matrix} S_{n} = \sqrt[]{1 + 1 + \frac{1}{4}} + \sqrt[]{1 + \frac{1}{4} + \frac{1}{9}} + ... + \sqrt[]{1 + \frac{1}{n^{2}} + \frac{1}{{(n + 1)}^{2}}} \end{matrix}

összeg értéke nem egész szám!

Második forduló

1. Bizonyítsuk be, hogy ha

x

y

tetszőleges valós számok, akkor az

\begin{matrix} x^{2} + 5 y^{2} - 4 x y + 2 x - 6 y + 3 \end{matrix}

kifejezés értéke pozitív.

2. Legyen

p

olyan

3

-nál nagyobb prímszám, amelynek

n

-edik hatványa húszjegyű (

n

pozitív egész). Bizonyítsuk be, hogy e húsz jegy között van három egyenlő.

3. Az

A B C D

konvex négyszög

A B

és

C D

oldalát osszuk fel

7

‐

7

egyenlő részre. Az

A B

és a

C D

oldalak

A

, illetve

D

csúcsától számított ugyanannyiadik osztópontjait összekötő szakaszok a négyszöget hét négyszögre vágják szét. Bizonyítsuk be, hogy a hét négyszög között van olyan, amelynek a területe az

A B C D

területének a hetedével egyenlő.

4. Bizonyítsuk be, hogy a

\begin{matrix} {(\sqrt[]{5} + 2)}^{1994} + {(\sqrt[]{10} + 3)}^{1995} \end{matrix}

összeg tizedesvessző előtti számjegye (azaz az egyes helyiértékű számjegye) 1-gyel egyenlő. (A feladat megoldásához számítógép nem használható.)

Harmadik (döntő) forduló

1. Az

A_{1} A_{2} A_{3} A_{4}

és

A_{1} B_{2} B_{3} B_{4}

közös csúcsú, azonos körüljárású különböző négyzetek. Bizonyítsuk be, hogy az

A_{2} B_{2}

A_{3} B_{3}

A_{4} B_{4}

egyenesek egy ponton mennek át.
Igaz-e a feladat következő általánosítása: ha

A_{1} A_{2} A_{3} ... A_{n}

és

A_{1} B_{2} B_{3} ... B_{n}

közös csúcsú, azonos körüljárású különböző szabályos

n

-szögek, akkor az

A_{2} B_{2}

A_{3} B_{3}

...

A_{n}

B_{n}

egyenesek egy ponton mennek át.

2. Jelölje egy tetszőleges konvex

n

-szög oldalait

a_{1}

a_{2}

...

a_{n}

; belső szögeit

α_{1}

α_{2}

...

α_{n}

, területét pedig

t

.
Mely

n

értékekre igaz bármely konvex

n

-szög esetén, hogy

\begin{matrix} \frac{a_{1}^{2} + a_{2}^{2} + ... + a_{n}^{2}}{t} \geq \frac{1}{sin α_{1}} + \frac{1}{sin α_{2}} + ... + \frac{1}{sin α_{n}} ? \end{matrix}

3. Legyenes

p

és

q

pozitív prímszámok. Tudjuk, hogy

\begin{matrix} \sqrt[]{p^{2} + 7 p q + q^{2}} + \sqrt[]{p^{2} + 14 p q + q^{2}} \end{matrix}

egész. Bizonyítsuk be, hogy

p = q

III. Kategória
(A gimnáziumok speciális matematikai osztályainak tanulói)

Első (iskolai) forduló

1. Van-e olyan

n

, amelyre az

1

-től

4 n

-ig terjedő egész számok elhelyezhetők egy

4

sorból és

n

oszlopból álló téglalapba úgy, hogy az utolsó sorban minden elem a fölötte álló három elemnek az összege legyen?

2. Legyen két egymást metsző kör

k_{1}

és

k_{2}

, az egyik közös pontjukat jelölje

A

. A két kör egyik közös érintője

k_{1}

-et

P

-ben,

k_{2}

-t

Q

-ban, a másik közös érintő

k_{1}

-et

R

-ben,

k_{2}

-t

S

-ben érinti. Bizonyítsuk be, hogy a

P A Q

és

R A S

háromszögek körülírt körei érintik egymást.

3. Melyik az a legkisebb pozitív egész szám, amely legalább hatféleképpen előáll négy darab különböző (pozitív) osztójának az összegeként?

4. Mutassuk meg, hogy ha egy

10

egységszer

8

egységszer

6

egységnyi oldalú téglatestben akárhogyan helyezünk is el

9

darab (egymásba nem nyúló) egységkockát, akkor biztosan elhelyezhető a téglatestben még egy egységnyi sugarú gömb is (amelynek nincs közös belső pontja egyik kockával sem és minden pontja a téglatestbe esik).

5. Egy dobozban

5

vásárlási utalvány van, értékük

100

200

300

400

, illetve

500

forint. A dobozból legfeljebb százszor húzhatunk egy-egy utalványt úgy, hogy minden húzás után visszatesszük a kihúzott papírt. Bármelyik húzás után leállhatunk (azaz többször nem húzunk), és akkor megtarthatjuk az éppen nálunk levő utalványt. Milyen szabály szerint álljunk le, hogy a várható nyereményünk a lehető legnagyobb legyen, és mennyi ez a maximális várható nyeremény?

Második (döntő) forduló

1. A

k

kör belülről érinti az

A B C

háromszög körülírt körét az

R

pontban, továbbá érinti az

A B

oldalt

P

-ben, az

A C

oldalt pedig

Q

-ban. Az

R P

, ill.

R Q

egyenesek másik metszéspontja a körülírt körrel

S

, ill.

T

, a

k

kör középpontja

U

. Bizonyítsuk be, hogy az

A U

B T

C S

és

P Q

egyenesek egy ponton mennek át.

2. Legyen

n

rögzített pozitív egész szám. Adjuk meg az

\begin{matrix} (x_{1} + x_{2} + ... + x_{n}) (\frac{1}{x_{1}} + \frac{1}{x_{2}} + ... + \frac{1}{x_{n}}) = \frac{9}{8} n^{2} \end{matrix}

egyenletnek az összes olyan megoldását a valós számok körében, ahol minden

i

-re

1 \leq x_{i} \leq 2

teljesül.

3. Számítsuk ki

m = 1995

esetén az alábbi összeg értékét:

\begin{matrix} \sum_{k = 0}^{m} (\binom{m}{k}) {(- 2)}^{k} (\binom{2 m - 2 k}{m - k}) . \end{matrix}

\sum_{k = 0}^{m}

jelölés azt jelenti, hogy a szóban forgó tagokat az összes

0 \leq k \leq m

értékre kell összegezni.

(\binom{0}{0})

értéke definíció szerint 1.)

Az 1994/95. évi matematika Országos Középiskolai Tanulmányi Verseny eredményei

I. kategória (A szakközépiskolák tanulói)

I. díj:

Németh Sándor Géza, IV. o., Vác, Boronkay György Műszaki Szakközépiskola, felkészítő tanár: Benedek Ilona

II. díj:

Zaupper Bence, III. o., Győr, Krúdy Gyula Gimnázium és Vendéglátóipari Szki., felkészítő tanár: Babarczi Imréné

III. díj:

Bányai Attila, IV. o., Kaposvár, Eötvös Loránd Műszaki Középiskola, felkészítő tanár: Demeter László

4.

Kiss Béla, II. o., Vác, Boronkay György Műszaki Szakközépiskola, felkészítő tanár: Újvári István

5.

Kiss Olivér, IV. o., Debrecen, Mechwart András Gépipari Műszaki Szki., felkészítő tanár: dr. Rutovszky Ede

6.

Stikkel Gábor, III. o., Eger, Neumann János Közgazdasági Szki. és Gimnázium, felkészítő tanár: Máté Mihályné

7.

Gál Marcell, IV. o., Budapest, Trefort Ágoston Kéttannyelvű Műsz. Szki. és Gimn., felkészítő tanár: Csapó Judit

8.

Novák András, IV. o., Kecskemét, Kada Elek Közgazdasági Szakközépiskola, felkészítő tanár: Szenesné Durucz Anna

9.

Pálos Ferenc, IV. o., Budapest, Trefort Ágoston Kéttannyelvű Műsz. Szki. és Gimn., felkészítő tanár: Csapó Judit

10.

Lovász Zoltán, IV. o., Bonyhád, Perczel Mór Közgazdasági Szakközépiskola, felkészítő tanár: Lohl Árpád
Miniszteri dicséretben részesült:
11. Szabó Ildikó, IV. o., Miskolc, Fáy András Közgazdasági Szki.; 12. Kovács Krisztián, IV. o., Békéscsaba, Kemény Gábor Műszaki Szki.; 13. Havasi László, III. o., Szeged, Kőrösi J. Közgazdasági és Külkereskedelmi Szki.; 14. Bartha Zoltán, IV. o., Budapest, Trefort Ágoston Kéttannyelvű Műsz. Szki. és Gimn.; 15. László Norbert, IV. o., Pápa, Jókai Mór Közgazdasági Szki.; 16. Vízhányó Attila, IV. o., Kecskemét, Kada Elek Közgazdasági Szki.; 17. Krausz Katalin, IV. o., Vác, Boronkay György Műszaki Szki.; 18. Bognár Zsolt, III. o., Kaposvár, Eötvös Loránd Műszaki Középiskola; 19. Barák Gábor, III. o., Békéscsaba, Széchenyi I. Közgazdasági és Külkereskedelmi Szki.; 20. Nagy Béla, IV. o., Békéscsaba, Széchenyi I. Közgazdasági és Külkereskedelmi Szki.; 21. Kardos Sándor Zsolt, IV. o., Budapest, Trefort Ágoston Kéttannyelvű Műsz. Szki. és Gimn.; 22. Csányi Zsolt, IV. o., Kiskunfélegyháza, Közgazdasági Szki.; 23. Hényel Erika, IV. o., Salgótarján, Táncsics Mihály Közgazdasági Szki.; 24. Bazsik András, IV. o., Budapest, Vásárhelyi Pál Kereskedelmi Szki.; 25. Czuppon Krisztina, IV. o., Zalaegerszeg, Csány László Közgazdasági Szki.; 26‐28. Mihajlik György, IV. o., Vác, Boronkay György Műszaki Szki.; Fűzéri Csaba, IV. o., Miskolc, Bláthy Ottó Villamosenergia-ipari Szki.; Tajti Imre, III. o., Egri Közgazdasági Szki.; 29. Börcsök Zsolt, III. o., Szeged, Déri Miksa Ipari Szki.; 30. Bogos Zsuzsa, IV. o., Szigetszentmiklós, Batthyány Kázmér Gimnázium és Közgazdasági Szki.

II. kategória
(Nem speciális matematika tantervű gimnáziumi tanulók)

I. díj:

Burcsi Péter, III. o., Pápa, Türr István Gimnázium és Óvónői Szki., felkészítő tanár: Németh Zsolt

II. díj:

Gilyén Péter, IV. o., Budapest, Piarista Gimnázium, felkészítő tanár: Varga László, Mazgon Gábor

III. díj:

Ehreth Imre, IV. o., Bonyhád, Petőfi Sándor Evengélikus Gimnázium, felkészítő tanár: Erdélyi János

4.

Nagy Lajos, IV. o., Miskolc, Földes Ferenc Gimnázium, felkészítő tanár: Szabadfalviné Kormányos Anikó

5.

Torma Péter, IV. o., Győr, Révai Miklós Gimnázium, felkészítő tanár: Nagy Róbert, Zsebők Ottó, Tamás Imre

6.

Horváth István, IV. o., Fonyód, Mátyás Király Gimnázium és Postaforgalmi Szki., felkészítő tanár: Bödör Márta

7.

Németh Tibor, IV. o., Győr, Révai Miklós Gimnázium, felkészítő tanár: Nagy Róbert, Zsebők Ottó, Tamás Imre

8.

Szíjártó Gábor, IV. o., Győr, Révai Miklós Gimnázium, felkészítő tanár: Tamás Imre

9.

Simonics Gábor, IV. o., Sátoraljaújhely, Kossuth Lajos Gimnázium és Egészségügyi Szki., felkészítő tanár: Dobó Józsefné

10.

Kovács Gábor, IV. o., Budapest, ELTE Radnóti Miklós Gyakorló Gimnázium, felkészítő tanár: Széplaki Györgyné

Miniszteri dicséretben részesült:
11. Farkas Péter, IV. o., Budapest, Szent István Gimnázium; 12. Izsák Ferenc, IV. o., Szombathely, Nagy Lajos Gimnázium; 13. Wágner Ferenc, IV. o., Tata, Eötvös József Gimnázium; 14. Varga Dezső, IV. o., Miskolc, Földes Ferenc Gimnázium; 15. Mikola István, IV. o., Sárospataki Református Gimnázium; 16. Kardkovács Zsolt, IV. o., Budapest, Károlyi Mihály Magyar‐Spanyol Tannyelvű Gimnázium; 17. Császár Miklós, IV. o., Szekszárd, Garay János Gimnázium; 18. Fekete Gergely, IV. o., Békéscsaba, Rózsa Ferenc Gimnázium; 19. Lestyán Zsolt, III. o., Kecskemét, Katona József Gimnázium; 20. Holcsek Balázs, III. o., Veszprém, Lovassy László Gimnázium; 21. Horváth Károly, IV. o., Sárvár, Tinódi Sebestyén Gimnázium; 22. Heim László, IV. o., Budapest, Kodály Zoltán Magyar Kórusiskola Gimnázium; 23. Szabó Balázs Zsolt, IV. o., Esztergom, Szent István Gimnázium és Híradástechnikai Szki.; 24. Lolbert Tamás, III. o., Szombathely, Nagy Lajos Gimnázium; 25. Sztranyák Attila, III. o., Kecskemét, Katona József Gimnázium; 26. Szabó Balázs, IV. o., Veszprém, Vetési Albert Gimnázium; 27. Benedik Marcell, IV. o., Budapest, ELTE Radnóti Miklós Gyakorló Gimnázium; 28. Tarján Péter, III. o., Budapest, Piarista Gimnázium; 29. Csorba István, IV. o., Győr, Révai Miklós Gimnázium; 30‐31. Oláh Judit, IV. o., Jászberény, Lehel Vezér Gimnázium; Tihon József, III. o., Budapest, Szent István Gimnázium.

III. kategória
(A speciális matematika tantervű gimnáziumok tanulói)

I. díj:

Koblinger Egmont, IV. o., Budapest, Fazekas Mihály Gyakorló Gimnázium, felkészítő tanár: Táborné Vincze Márta, Thiry Imréné

II. díj:

Szádeczky-Kardoss Szabolcs, IV. o., Budapest, Fazekas Mihály Gyakorló Gimnázium, felkészítő tanár: Táborné Vincze Márta, Thiry Imréné

III. díj:

Bárász Mihály, III. o., Budapest, Fazekas Mihály Gyakorló Gimnázium, felkészítő tanár: Surányi László, Beleznay Ferenc, Dobos Sándor

4.

Tóth Gábor Zsolt, III. o., Budapest, Árpád Gimnázium, felkészítő tanár: Mikusi Imre, Vajda István

5.

Németh Zoltán, IV. o., Budapest, Fazekas Mihály Gyakorló Gimnázium, felkészítő tanár: Táborné Vincze Márta, Thiry Imréné

6.

Valkó Benedek, IV. o., Budapest, Fazekas Mihály Gyakorló Gimnázium, felkészítő tanár: Táborné Vincze Márta, Thiry Imréné

7.

Horváth Péter, IV. o., Budapest, Fazekas Mihály Gyakorló Gimnázium, felkészítő tanár: Táborné Vincze Márta, Thiry Imréné

8.

Fey Dániel, IV. o., Budapest, Fazekas Mihály Gyakorló Gimnázium, felkészítő tanár: Táborné Vincze Márta, Thiry Imréné

9.

Fenyvesi Anikó, IV. o., Székesfehérvár, Teleki Blanka Gimnázium, felkészítő tanár: Mihályi Gyula, Láng Hugó

10.

Ruzsa Gábor, III. o., Budapest, Fazekas Mihály Gyakorló Gimnázium, felkészítő tanár: Surányi László, Beleznay Ferenc, Dobos Sándor

Miniszteri dicséretben részesült:
11. Elek Péter, III. o., Budapest, Árpád Gimnázium; 12. Szobonya László, III. o., Budapest, Fazekas Mihály Gyakorló Gimnázium; 13. Kovács András, III. o., Budapest, Fazekas Mihály Gyakorló Gimnázium; 14. Tóth Péter, III. o., Miskolc, Földes Ferenc Gimnázium; 15. Bárász Tamás, III. o., Budapest, Fazekas Mihály Gyakorló Gimnázium; 16. Orbán András, III. o., Budapest, Fazekas Mihály Gyakorló Gimnázium; 17. Király Csaba, III. o., Budapest, Fazekas Mihály Gyakorló Gimnázium; 18. Kiss Márton, III. o., Budapest, Fazekas Mihály Gyakorló Gimnázium; 19. Hegedüs Márton, III. o., Budapest, Fazekas Mihály Gyakorló Gimnázium; 20. Józsa Balázs Gábor, IV. o., Budapest, Fazekas Mihály Gyakorló Gimnázium.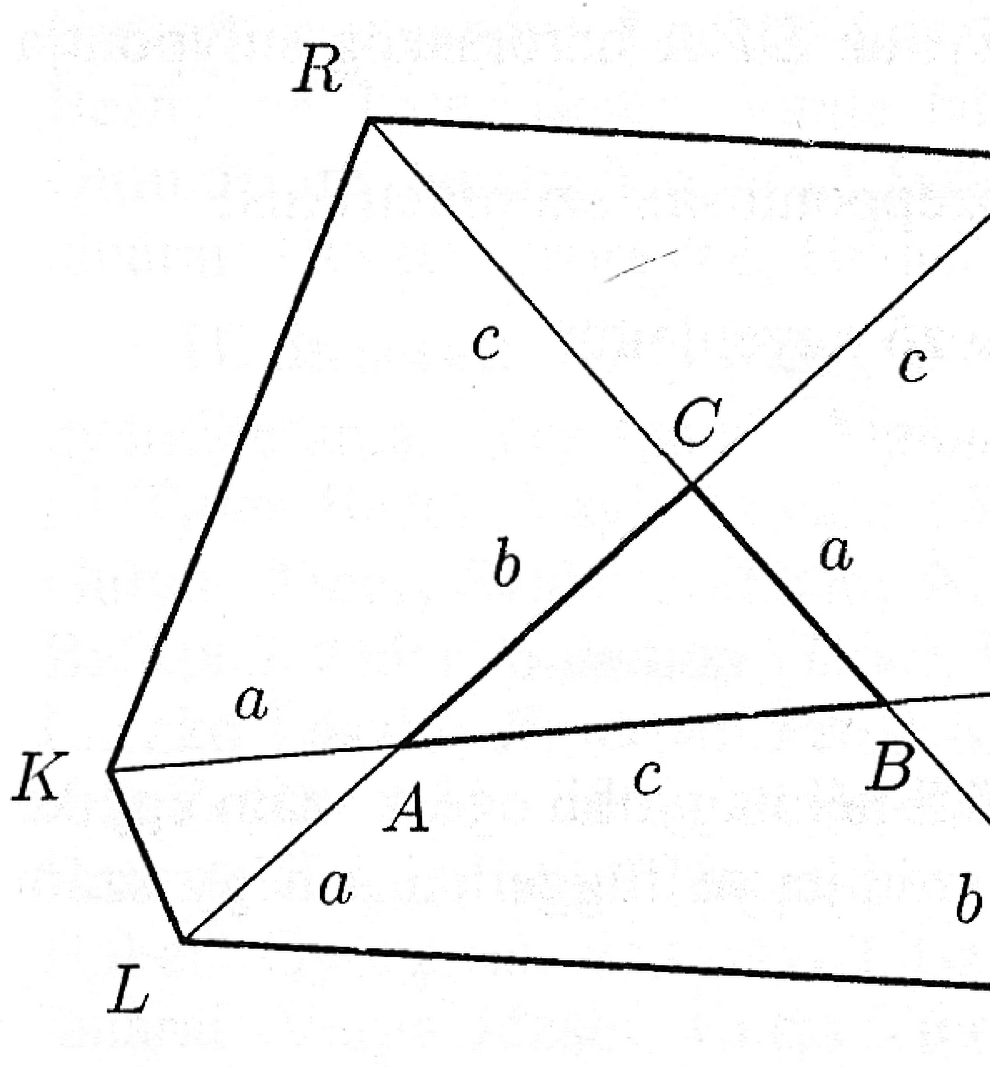