Cím:	1994. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldása
Szerző(k):	Surányi János
Füzet:	1995/február, 67 - 73. oldal	PDF  |  MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd)

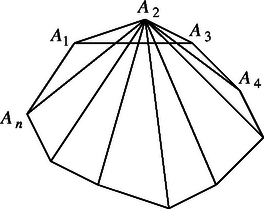
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   1. Jelölje egy paralelogramma két szomszédos oldalának az arányát $\lambda$ (ahol $\lambda >1$). Határozzuk meg, hogy hogyan függ $\lambda$-tól az átlók közti hegyesszög legnagyobb lehetséges értéke.   I. megoldás. Tekintsünk egy $ABCD$ paralelogrammát, amelyikben $AB$ és $BC$ hossza $a$, illetőleg $\lambda a$ ($\lambda >1$), az átlók metszéspontja és a $BC$ oldal felezőpontja $E$, illetőleg $F$. Ekkor $E$ egyben az átlók közös felezőpontja is, így $EF$ az $AB$-vel párhuzamos középvonal fele, hossza $\frac{1}{2}a$. A szóba jövő $E$ pontok tehát az $F$ középpontú, $\frac{1}{2}a$ sugarú $k_E$ kör pontjai, kivéve a $BC$ egyenessel való két metszéspontot, amelyek a kör átellenes pontjai. Szimmetria okokból elég a $BC$ egyenes egyik oldalán levő félkört vizsgálni (1. ábra).   1. ábra   A kör átmérője a $BC$ szakasz része. Az átlók szöge a $BC$ szakasz látószöge $E$-ből, tehát tompaszög (hiszen az átmérő látószöge derékszög). Ennek az $\alpha$ szögnek a lehető legkisebb értékét kell tehát meghatároznunk. Belátjuk, hogy $\alpha$ értéke a félkör $E_0$ felezőpontjára a legkisebb. A $BC{E}_0$ háromszög köré írt $k_0$ kört belülről érinti $k_E$, mert mindkét kör középpontja a $BC$-re $F$-ben emelt merőlegesen van, és $k_E$ átmérője a $BC$ szakasz része. A $DE$ és $k_0$ metszéspontját $G$-vel jelölve $\begin{array}{c}{\displaystyle CEB\sphericalangle =CGB\sphericalangle +GCE\sphericalangle >CGB\sphericalangle =C{E}_{0}B\sphericalangle \mathrm{,}}\end{array}$ amint állítottuk. A keresett legnagyobb hegyesszög, ${\phi }_0$ ennek a szögnek mellékszöge, és mivel a $BC{E}_0$ háromszög egyenlő szárú, az $E_{0}BF\sphericalangle$ kétszeresével egyenlő, tehát például így fejezhető ki $\lambda$-val a $B{E}_{0}F$ derékszögű háromszögből: $\begin{array}{c}{\displaystyle \text{<span style="font-weight: normal;font-style: normal;">ctg</span>}\frac{{\phi }_0}{2}=\frac{BF}{E_{0}F}=\frac{\frac{1}{2}\lambda a}{\frac{1}{2}a}=\lambda \mathrm{,}\text{azaz}{\phi }_0=2\text{<span style="font-weight: normal;font-style: normal;">arcctg</span>}\lambda \mathrm{,}}\end{array}$ ahol az arkusz-függvény $0^{\circ }$ és ${90}^{\circ }$ közé eső értékét kell venni.   Megjegyzés. A feladat szövege feltételezte ugyan, de meggondolásaink során bizonyítást is nyert, hogy ezt a maximális értéket fel is veszi az átlók szöge, és azt is beláttuk, hogy a téglalapban a legnagyobb ez a szög.   II. megoldás. Válasszuk mértékegységnek az $AB$ oldal hosszát, ekkor $BC$ hossza $\lambda$. Jelöljük az átlók metszéspontját (ami közös felezőpontjuk is) $E$-vel, $AE$ és $EB$ hosszát $e$-vel, illetőleg $f$-fel, a köztük levő szöget $\phi$-vel (2. ábra). A koszinusztételt alkalmazzuk az $AEB$ és a $BEC$ háromszögre. $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle 1}& {\displaystyle =e^2+f^2-2ef\text{cos}\phi \mathrm{,}}\hfill \\ \hfill {\displaystyle {\lambda }^2}& {\displaystyle =e^2+f^2-2ef\text{cos}\left({180}^{\circ }-\phi \right)=e^2+f^2+2ef\text{cos}\phi \mathrm{.}}\hfill \end{array}}}\end{array}$ A megfelelő oldalak összegét és különbségét képezve $\begin{array}{c}{\displaystyle {\lambda }^2+1=2\left(e^2+f^2\right)\mathrm{,}{\lambda }^2-1=4ef\text{cos}\phi \mathrm{.}}\end{array}$   2. ábra   A második egyenlőség bal oldala pozitív, így $\text{cos}\phi$ pozitív, $\phi$ tehát hegyesszög. Alkalmazzuk a második egyenlőségben $e^2$-re és $f^2$-re a mértani és számtani közép közti egyenlőtlenséget, és használjuk fel az első egyenlőtlenséget: $\begin{array}{c}{\displaystyle {\lambda }^2-1\le 4\left(\frac{e^2+f^2}{2}\right)\text{cos}\phi =\left({\lambda }^2+1\right)\text{cos}\phi \mathrm{.}}\end{array}$ Innen $\begin{array}{c}{\displaystyle \text{cos}\phi \ge \frac{{\lambda }^2-1}{{\lambda }^2+1}\mathrm{,}}\end{array}$ és akkor áll fenn egyenlőség, ha $e=f$, azaz ha a paralelogramma téglalap. Mivel a koszinusz-függvény a $\left(0^{\circ };{90}^{\circ }\right)$ számközben a változó csökkenő függvénye, így a keresett legnagyobb ${\phi }_0$ szögre $\begin{array}{c}{\displaystyle \text{cos}{\phi }_0=\frac{{\lambda }^2-1}{{\lambda }^2+1}\mathrm{,}{\phi }_0=\text{arc}\text{cos}\frac{{\lambda }^2-1}{{\lambda }^2+1}\mathrm{,}}\end{array}$ ahol a függvény $0^{\circ }$ és ${90}^{\circ }$ közé eső értékét kell venni.   Megjegyzés. A $\begin{array}{c}{\displaystyle \text{cos}\alpha =\frac{\text{cos}{}^2\left(\alpha /2\right)-\text{sin}{}^2\left(\alpha /2\right)}{\text{cos}{}^2\left(\alpha /2\right)+\text{sin}{}^2\left(\alpha /2\right)}=\frac{\text{<span style="font-weight: normal;font-style: normal;">ctg</span>}{}^2\left(\alpha /2\right)-1}{\text{<span style="font-weight: normal;font-style: normal;">ctg</span>}{}^2\left(\alpha /2\right)+1}}\end{array}$ azonosság alapján világos, hogy az eredmény megegyezik az előző megoldásban nyerttel.   III. megoldás. Az $AC$ átlót rögzítve azok a $D$ pontok, amelyekre az $AD/CD$ arány egy rögzített (1-nél nagyobb) $\lambda$ érték, egy kört alkotnak, az $AC$ szakaszhoz és $\lambda$ arányhoz tartozó Apolloniosz-kört. Jelöljük ezt $k_{\lambda }$-val, $AC$ felezőpontját $E$-vel, $k_{\lambda }$ középpontját $O$-val. Az $AC$ és $ED$ átlók közti szög akkor a legnagyobb, ha $D$ az $E$ pontból a $k$ körhöz húzott érintő $D_0$ érintési pontja. Jelöljük ezt a legnagyobb szöget ${\phi }_0$-val, $k_{\lambda }$-nak az $AC$-re eső átellenes pontjait $P$-vel és $Q$-val, az $AC$ szakasz felét $e$-vel (3. ábra). $P$ és $Q$ ezt a szakaszt belülről, illetőleg kívülről $\lambda :1$ arányban osztó pont, így $\begin{array}{c}{\displaystyle \lambda =\frac{AP}{PC}=\frac{AQ}{QC}\mathrm{.}}\end{array}$   3. ábra   A szereplő szakaszokat $e$-vel fejezve ki a két törtben $\begin{array}{c}{\displaystyle \lambda =\frac{e+EP}{e-EP}=\frac{EQ+e}{EQ-e}\mathrm{.}}\end{array}$ (1) A második egyenlőségből a törtek eltávolítása és rendezés után az $\begin{array}{c}{\displaystyle e^2=EP\cdot EQ}\end{array}$ (2) egyenlőséget kapjuk. (1)-ből $\begin{array}{c}{\displaystyle EP=\frac{\left(\lambda -1\right)e}{\lambda +1}\mathrm{,}EQ=\frac{\left(\lambda +1\right)e}{\lambda -1}\mathrm{.}}\end{array}$ A (2) egyenlőség jobb oldalán álló szorzat az $E$ pontnak a $k_{\lambda }$ körre vonatkozó hatványa, így az egyenlőség azt jelenti, hogy az $E$ pontból a $k_{\lambda }$ körhöz húzott érintő hossza $E{D}_0=e$. A ${\phi }_0$ szög meghatározásakor az $OE{D}_0$ háromszög $O{D}_0$ oldalát, vagyis a $k_{\lambda }$ kör $r$ sugarát fejezzük ki $e$-vel és $\lambda$-val. $\begin{array}{c}{\displaystyle r=\frac{1}{2}PQ=\frac{1}{2}\left(EQ-EP\right)=\frac{1}{2}\left(\frac{\lambda +1}{\lambda -1}-\frac{\lambda -1}{\lambda +1}\right)e=\frac{2\lambda e}{{\lambda }^2-1}\mathrm{.}}\end{array}$ Az $EO{D}_0$ derékszögű háromszögből tehát $\begin{array}{c}{\displaystyle \text{<span style="font-weight: normal;font-style: normal;">tg</span>}{\phi }_0=\frac{r}{e}=\frac{2\lambda }{{\lambda }^2-1}\mathrm{,}{\phi }_0=\text{arc}\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\frac{2\lambda }{{\lambda }^2-1}\mathrm{,}}\end{array}$ ahol a $0^{\circ }$ és ${90}^{\circ }$ közé eső értékeket kell venni.   Megjegyzések. 1. Az előző megoldásokkal való kapcsolat könnyen adódik például a $\begin{array}{c}{\displaystyle \text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha =\frac{2\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\frac{\alpha }{2}}{1-\text{<span style="font-weight: normal;font-style: normal;">tg</span>}{}^2\frac{\alpha }{2}}=\frac{2\text{<span style="font-weight: normal;font-style: normal;">ctg</span>}\frac{\alpha }{2}}{\text{<span style="font-weight: normal;font-style: normal;">ctg</span>}{}^2\frac{\alpha }{2}-1}}\end{array}$ összefüggésből.   2. Az $E{D}_0=e$ egyenlőség szerint $D_0$ az $AC$ átmérőjű körön van, így az $AC{D}_0$ háromszög derékszögű, vagyis az a paralelogramma, amelyikre az átlók szöge a legnagyobb, a téglalap.   2. Bizonyítsuk be, hogy ha egy konvex $n$-szög átlói közül elhagyunk bárhogyan $n-3$-at, a megmaradók közül mindig kiválasztható $n-3$ úgy, hogy ne messék egymást a sokszög belsejében; viszont el lehet hagyni $n-2$ átlót úgy, hogy ez már ne legyen igaz.   Megoldás. A feladat állításainak bizonyításához előrebocsátunk néhány megjegyzést. Világos, hogy egy konvex sokszögben addig húzhatunk meg egymást nem metsző átlókat, amíg a sokszöget csupa háromszögre nem bontjuk. (A közös végpontokat a következőkben nem tekintjük metszéspontnak.) Ismeretes, hogy bárhogyan történik ez a felbontás, konvex $n$-szögben ehhez $n-3$ átló szükséges, és azok $n-2$ háromszöget hoznak létre. (Lásd pl. Matematikai Versenytételek III., 1985. évi 1. feladat 2. megjegyzés, 295. oldal.) A feladat két állítás bizonyítását kívánja. Az elsőt teljes indukcióval bizonyítjuk. Nyilvánvaló az állítás helyessége háromszögekre ($0$ átló elhagyása után meghúzható $0$ egymást nem metsző átló), és négyszögekre is. Legyen a továbbiakban $m\ge 5$, egy konvex $m$-szög $A_1{A}_2\text{...}{A}_m$, és tegyük fel, hogy konvex $\left(m-1\right)$-szögekre igaz az állítás. Legyen az $m$-szögben elhagyva tetszés szerint $m-3$ át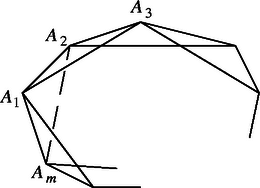ló.   4. ábra   Nézzük a második szomszéd csúcsokat összekötő átlókat, nevezzük ezeket a továbbiakban kis átlóknak. Mivel $m\ge 5$, minden kis átlóhoz egyértelműen tartozik a végpontjai közti, azaz a kis átló által lemetszett csúcs. A kis átlók száma tehát $m$, s így nincs mindegyik elhagyva. Van köztük olyan, amelyik nincs elhagyva, de az általa levágott csúcsból induló átlók közt van elhagyott. Ez nyilvánvaló, ha az elhagyott átlók közt nincs kis átló. Ha nem ez a helyzet, akkor pl. $A_1{A}_3$, $A_2{A}_4$, $\text{...}$, $A_{m-1}{A}_1$, $A_m{A}_2$ sorrendben végighaladva a kis átlókon találunk el nem hagyottat, amire következő el van hagyva. Válasszuk a számozást úgy, hogy $A_2{A}_m$ nincs elhagyva, $A_1{A}_3$ el van hagyva. Ekkor az $A_2\text{...}{A}_m$ konvex $\left(m-1\right)$-szög átlói az eredeti sokszögben is átlók, és közülük legfeljebb $m-4$ van elhagyva, mert az $A_1{A}_3$ elhagyott átló az $\left(m-1\right)$-szög átlói közt nem szerepel (4. ábra). Így az $\left(m-1\right)$-szögben meghúzható $m-4$ egymást nem metsző átló az el nem hagyottak közül. Az $m$-szögben ezekhez hozzávehetjük az $A_2{A}_m$ átlót, mert ez az $\left(m-1\right)$-szögnek oldala, így egyrészt nincs a meghúzott átlók között, másrészt nem metszi azokat. Az állítás helyessége tehát öröklődik az $m$-szögre is, így minden konvex sokszögre igaz. A második állítás igazolására megadunk egy $A_1{A}_2\text{...}{A}_n$ konvex $n$-szögben $n-2$ átlót úgy, hogy azok elhagyása után ne lehessen a maradók közül $n-3$ nem metszőt kiválasztani. Erre több lehetőség is kínálkozik. 1. Hagyjuk el az $A_2$-ből induló átlókat és $A_1{A}_3$-at (5. ábra). A maradó átlók éppen az $A_1{A}_3\text{...}{A}_n$  $\left(n-1\right)$-szög átlói. Ezek közül kellene $n-3$ egymást nem metszőt kiválasztani. Láttuk azonban, hogy ebből csak $n-1-3=n-4$ nem metsző átló választható ki. Ezzel igazoltuk a második állítást.   5. ábra   6. ábra   2. A második állítás igazolására alkalmas az is, ha a kis átlókat hagyjuk el az $A_1{A}_3$ és az $A_2{A}_4$ kivételével (6. ábra). Ismeretes ugyanis, hogy egy konvex $n$-szögben tetszés szerinti $n-3$ nem metsző átló közt mindig van legalább két kis átló. (A korábban idézett helyen a 3. megjegyzés c) pontja, 295. oldal.) A leírt elhagyás mellett azonban csak két meghúzható kis átló van, de azok metszik egymást. Ezzel újabb bizonyítást adtunk a második állításra. 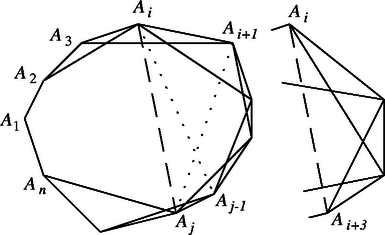  7. ábra   Megjegyzések. 1. A versenyzők a fentiekben idézett segédtételek közül azokat, amelyeket felhasználtak, be is bizonyították.   2. Az első állításnál négyszög esetén bármelyik átlót hagyjuk el, a másikat kell kiválasztanunk. Megadunk $n\ge 5$-re is $n-3$ átlót úgy, hogy azok elhagyása esetén csak egyféleképpen lehessen $n-3$ nem metsző átlót kiválasztani. Ehhez ötletet ad a 2. állítás igazolására adott 2. ellenpélda és annak igazolása. Hagyjuk el az $A_1{A}_2\text{...}{A}_n$ sokszögből a kis átlókat, kivéve az $A_{n-1}{A}_1$, az $A_n{A}_2$ és az $A_1{A}_3$ átlót. Ekkor egyedül az $A_1$ csúcsból induló átlók kiválasztása ad megoldást. Állításunk igazolására megmutatjuk, hogy semelyik $A_i{A}_j$ átló sem szerepelhet a kiválasztottak közt, ha $2\le i<j\le n$ (7. ábra). Mivel átlóról van szó, és az $A_i{A}_{i+2}$ átló el van hagyva, így $A_i\text{...}{A}_j$ legalább 4-oldalú konvex sokszög, és ebben legfeljebb az $A_i{A}_{j-1}$ és $A_{i+1}{A}_j$ kis átló nincs elhagyva, ezek azonban metszik egymást. ($j=i+3$ esetén ezek is elhagyott átlók.) Ezzel igazoltuk az állítást.   3. Adottak a $H_1$, $H_2$, $\text{...}$, $H_n$ halmazok. A $H_k$ halmaz $\left(k=\mathrm{1,2,}\text{...}\mathrm{,}n\right)$ a valós számegyenes $k$ darab olyan intervallumából áll, amelyeknek páronként nincs közös pontja. Bizonyítsuk be, hogy a fenti $H_k$ halmazokat alkotó intervallumok közül kiválasztható $\left[\left(n+1\right)/2\right]$ olyan intervallum, amelyek mindegyike más-más $H_k$ halmazhoz tartozik, és semelyik kettőnek nincs közös pontja. ($\left[x\right]$ a legnagyobb egész szám, amelyik kisebb az $x$-nél vagy egyenlő vele.)   Megoldás. A következő állítást fogjuk bizonyítani: Ha az $L_1$, $L_2$, $\text{...}$, $L_m$ halmaz mindegyike a számegyenes legalább $m$ (de véges számú) páronként közös elem nélküli intervallumából áll, akkor kiválasztható mindegyik halmazból egy-egy intervallum úgy, hogy semelyik kettőnek ne legyen közös pontja. Ez tartalmazza a feladat állítását. Ehhez csak $n=2m-1$ és $n=2m$ esetén a $H_m$, $H_{m+1}$, $\text{...}$, $H_{2m-1}$ halmazokra kell alkalmazni a kimondott tételt. Az állítás igaz, ha $m=1$. Ha $m>1$, eljárást adunk meg az intervallumok egymás utáni kiválasztására. Vegyük mindegyik halmaz balról első intervallumának a jobb végpontját és azt vagy azokat az intervallumokat, amelyekre ez a legkisebb. Több intervallum esetén válasszunk ki egy jobbról nyitottat, ha van ilyen, különben tetszés szerint egyet. Legyen ez $I_1$, és tartozzék az $L_i$ halmazhoz. Ezután hagyjuk el $L_i$-t, a többi halmazból pedig a balról első intervallumot, majd ismételjük az eljárást, amíg el nem fogynak a halmazok. Az első lépés után $m-1$ halmaz marad, mindegyik legalább $m-1$ páronként közös pont nélküli intervallumból áll. Azt kell még belátnunk, hogy $I_1$-nek a megmaradt intervallumok egyikével sincs közös pontja. Ezzel egyenértékű az, hogy ha $I_1$-nek az eredeti $L_j$ halmaz $I\text{'}$ intervallumával van közös pontja, ahol $j\ne i$, akkor $I\text{'}$ az $L_j$ balról első intervalluma. Jelöljük $I\text{'}$ bal végpontját $b$-vel, és tegyük fel, hogy van $L_j$-ben egy $I\text{'}$-től balra levő $I\text{'}\text{'}$ intervallum. Ha $b$ kisebb $I_1$ jobb végpontjánál, akkor ez még inkább igaz $I\text{'}\text{'}$ jobb végpontjára (8.a ábra; a halmazokat párhuzamosan eltolt egyeneseken szemléltetjük), így nem $I_1$-et kellett volna kiválasztanunk. 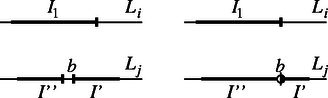  8. ábra   Ha $b$ egyenlő $I_1$ jobb végpontjával, akkor kell, hogy $I\text{'}$ balról, $I_1$ jobbról zárt legyen. Ekkor $I\text{'}\text{'}$ jobb végpontja vagy kisebb $b$-nél, vagy egyenlő vele, de az utóbbi esetben az intervallum nyitott, mert nincs közös pontja $I\text{'}$-vel (8.b ábra). Ismét egyik esetben sem $I_1$-et kellett volna kiválasztani eljárásunk szerint. Ezzel bebizonyítottuk az állítást. Ezek alapján az eljárást $m$-szer megismételve az összes követelményt kielégítő intervallumhalmazt kapunk.   Megjegyzés. Többen tettek kísérletet annak bizonyítására, hogy a feladat állításában az $\left[\frac{n+1}{2}\right]$ korlát nem javítható, de ezek hibásak. Az $\left[\frac{n+1}{2}\right]$ élességét csupán $n\le 6$-ra sikerült eddig belátni. Annyit azonban meg lehet mutatni, hogy van olyan halmazrendszer, amelyikből csak $\left(1-\frac{1}{e}\right)\left(n+1\right)$-nél kevesebb intervallum választható ki a feladat követelményeinek megfelelően.   9. ábra   Álljon $k=1$, 2, $\text{...}$, $n$-re $H_k$ a $\begin{array}{c}{\displaystyle \left(\mathrm{0,1}/k\right)\mathrm{,}\left(1/k\mathrm{,2}/k\right)\mathrm{,}\text{...}\mathrm{,}\left(\left(k-1\right)/k\mathrm{,1}\right)}\end{array}$ nyitott intervallumokból. Legyen a kívánalmaknak megfelelően kiválasztható intervallumok maximális száma $j$. A kiválasztott intervallumok hosszának az összege nem lehet 1-nél nagyobb. Ha minden lépésben kiválaszthatunk egyet a megmaradt legrövidebb intervallumok közül, ez az összeg akkor is legalább $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle S=\frac{1}{n}+\frac{1}{n-1}+\text{...}+\frac{1}{n-j+1}=}\\ \hfill {\displaystyle =\frac{1}{n}\cdot \left(1+\frac{1}{1-1/n}+\frac{1}{1-2/n}+\text{...}+\frac{1}{1-\left(j-1\right)/n}\right)\mathrm{.}}\end{array}}}\end{array}$ Integrálva $\frac{1}{1-x}$-et $-\frac{1}{n}$-től $\frac{j-1}{n}$-ig, $S$ tekinthető az integrál egy felső közelítő összegének (9. ábra), s így az integrálnak 1-nél kisebbnek kell lennie, azaz $\begin{array}{c}{\displaystyle \text{log}\left(\frac{n+1}{n-j+1}\right)<\mathrm{1,}j<\left(1-\frac{1}{e}\right)\left(n+1\right)\mathrm{.}}\end{array}$ Ez tehát felső korlát a kiválasztható intervallumok számára. A nyert konstans: $\begin{array}{c}{\displaystyle 1-\frac{1}{e}=0\mathrm{,}63212\text{...}}\end{array}$ A megjegyzés Surányi Lászlótól származik.